GF-2星全色相机在轨MTF测量和图像复原研究

王治中， 张庆君

(1.中国空间技术研究院总体部,北京 100086； 2.中国资源卫星应用中心,北京 100094)



GF-2星全色相机在轨MTF测量和图像复原研究

王治中1,2， 张庆君1

(1.中国空间技术研究院总体部,北京 100086； 2.中国资源卫星应用中心,北京 100094)

调制传递函数(modulation transfer function,MTF)不仅是监测遥感卫星光学相机在轨运行情况和性能的有效手段，也是对卫星图像进行复原处理的重要参数。利用刀刃法对高分二号(GF-2)卫星全色相机进行MTF在轨测量。在计算MTF的过程中，使用汉明窗对截取后的线扩展函数(line spread function,LSF)曲线进行处理，以抑制截取过程所造成的频谱泄露。此外，还对截取后LSF曲线的两端补0，扩展LSF曲线的长度，以提高傅里叶变换时的采样频率。实验结果表明，使用本文刀刃法计算所得的MTF采样密度比传统方法提高了5倍，使得MTF曲线更为平滑，提高了MTF的数值精度，有利于后续的图像复原处理。基于传统刀刃法和本文刀刃法计算所得的MTF测量结果，采用维纳滤波法分别对GF-2全色图像进行复原处理研究。结果表明，对2种方法得到的MTF测量结果的维纳滤波均可明显提高图像的清晰度和边缘细节信息； 但使用本文方法得到的MTF结果可使复原后的图像在对比度、边缘能量和平均梯度等关键指标上均优于使用传统方法得到的MTF结果。

高分二号卫星； MTF在轨测量； 刀刃法； 图像复原； 维纳滤波

0 引言

高分二号(GF-2)卫星是我国高分专项工程的第二颗卫星，也是我国迄今最新发射的亚m级高分辨率卫星。自2014年8月19日成功发射以来，GF-2卫星已经向国土资源部、住房城乡建设部、交通运输部、国家林业局等用户部门提供了上千景图像，并应用于我国国土资源调查、农业估产、环境保护及减灾救灾等领域。在轨测试期间，GF-2卫星还为云南鲁甸地震、景谷地震、四川康定地震、智利地震、印度泥石流以及北京APEC会议等重大事件提供了有效的服务。2015年3月6日，在成功完成在轨测试任务后，GF-2卫星正式交付使用。

卫星的颤振、偏流角等因素会导致相机在成像过程中产生像点位移，破坏光电荷移动的同步性，影响成像质量。此外，光学系统、大气扰动、电子噪声等也会对在轨运行卫星的图像产生退化作用[1]。调制传递函数(modulation transfer function,MTF)是评价光学系统性能的重要参数，被广泛用于卫星光学相机成像性能的在轨监测。MTF在轨测量方法有点脉冲法、正弦输入法、刀刃法和脉冲法等，其中刀刃法最为常用[2-3]。在图像退化模型中，MTF是点扩展函数(point spread function,PSF)在频域中的表示，图像退化的诸多因素均可以造成MTF下降。因此，基于MTF对图像进行补偿、进而对图像进行复原处理，可以提高图像清晰度和改善图像质量[4]。常用的图像复原方法有逆滤波、修正反转滤波和维纳滤波等[5-6]。近年来，研究人员还提出了一些新的图像复原算法。孟伟等[7]将逆滤波和维纳滤波相结合，提出一种二次复原算法。张凡[8]从支撑域和背景灰度值2个方面对经典非负支撑域有限递归逆滤波方法进行改进，并优化了代价函数。

本文利用刀刃法对GF-2卫星全色相机的MTF进行在轨测量。传统刀刃法在计算MTF过程中需要先对线扩展函数(line spread function,LSF)曲线进行裁剪，以降低LSF曲线两端抖动对MTF计算精度的影响； 再对截取后的LSF曲线进行傅里叶变换，得到MTF曲线。由于直接对截取后的LSF曲线进行傅里叶变换会导致频谱泄露，徐航等[9]利用汉明窗裁剪后的LSF曲线进行处理，以抑制频谱泄露。经离散傅里叶变换后，MTF曲线的采样密度取决于LSF曲线截取的像元宽度。如果为了增加MTF曲线的采样密度而增加LSF截取的像元宽度，就会增加MTF曲线计算结果的噪声影响，而且也会增加选取刃边目标的难度[3]。王先华等[2]对截取后的LSF曲线两端补0，可以提高MTF曲线的频率密度。本文将以上2项改进措施结合起来，以便提高MTF的测量精度、进而优化图像复原效果。首先使用汉明窗对截取后的LSF进行处理，抑制截取过程造成的频谱泄露； 然后在截取后的LSF曲线两端补0，提高对MTF真实曲线的逼近程度； 最后利用MTF测量结果对图像进行维纳滤波，得到复原后的图像。结果表明，用本文方法计算得到的MTF曲线频率密度比传统方法提高5倍，MTF曲线更为平滑，提高了测量精度。经分析，本文方法和传统方法计算的MTF结果用于维纳滤波复原处理后，均可明显提高图像清晰度和边缘细节信息； 但使用本文方法得到的MTF结果可以使复原后的图像在对比度、边缘能量和空间频率等关键指标上均优于传统方法。

1 理论与方法

1.1 刀刃法测量MTF

刀刃法无需人工对在轨卫星的相机输入激励信号，可选择具有一定反差的2块相邻的亮暗均匀地物的人工铺设靶标或者自然直边景物(如大型建筑物、机场跑道、高速公路等)作为刃边目标。刀刃法对图像采样质量要求高，求解MTF的精度高，适合用于高分辨率卫星图像。

假设光学成像系统为线性不变系统h(x,y)，输入图像为i(x,y)，则输出图像g(x,y)满足

g(x,y)=i(x,y)*h(x,y) ；

(1)

假设光学系统的点扩散函数具有二维可分离性，则光学系统的响应函数可表示为

h (x,y)=h(x)·h(y) 。

(2)

式(1)―(2)中：h(x)为垂轨方向的一维响应函数；h(y)为沿轨方向的一维响应函数； *为卷积运算符。

垂轨方向的边缘扩展函数(edge spread function,ESF)可表示为

g(x)=i(x)*h(x) ，

(3)

式中i(x)为垂轨方向亮暗突变的刃边目标函数，亦称为阶跃函数。对阶跃函数求微分并归一化，可得到冲激函数。因此，对式(3)进行微分可得到冲激函数δ(x)，即

(4)

式(4)表明，对垂轨方向的ESF进行微分，可以得到系统在垂轨方向的一维响应函数，又称为垂轨方向的LSF； 对其归一化后再进行傅里叶变换，即可得到垂轨方向上的MTF。同理，可以求出沿轨方向的MTF，进而获得卫星相机的二维MTF矩阵。

在传统刀刃法基础上，本文计算沿轨方向MTF的步骤如下：

1)根据刃边目标边缘的亮度分布，寻找每行图像的亚像元边缘点。①对图像按列差分，求出每行图像的像元级边缘点； ②使用三次多项式拟合方法，求出每行图像的亚像元边缘点；

2)提取ESF曲线。①对图像的亚像元边缘点进行拟合，得到刃边直线； ②以拟合后的刃边为基准，对每行像元进行配准，使每行的亚像元边缘点正好落在拟合直线上； ③对每行图像进行三次样条插值，得到每行的ESF曲线； ④对每行ESF曲线相加求平均，得到平均ESF曲线；

3)提取LSF曲线。①对步骤2)得到的ESF曲线进行差分，并归一化，求出初始LSF曲线； ②对初始LSF曲线的2端进行裁剪，以消除噪声； ③用汉明窗对裁剪后的LSF曲线进行处理，减少频谱泄露的影响； ④对LSF曲线两端进行补零，增加傅里叶变换后MTF曲线的采样频率，提高曲线的平滑度；

4)对步骤3)得到的LSF曲线进行傅里叶变换，并归一化，得到沿轨方向MTF曲线。

1.2 维纳滤波图像复原

式(1)表示理想情况下光学系统在空域中的成像模型。如果考虑加性噪声的影响，则式(1)可改写为

g(x,y)=i(x,y)*h(x,y)+n(x,y) ，

(5)

式中n(x,y)为加性噪声。

对式(5)进行傅里叶变换，可得频域中的成像模型，即

G(u,v)=I(u,v)·H(u,v)+N(u,v) ,

(6)

式中H(u,v)为系统在频域中的响应函数，其幅值为MTF。

维纳滤波通过最小均方误差期望估计的控制条件，克服频率补偿的噪声放大问题。维纳滤波器可表示为

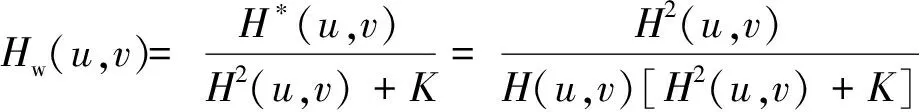
(7)

式中：H*(u,v)为H(u,v)的共轭；K为图像与噪声的功率谱之比，通常取常数。

使用维纳滤波器算子Hw(u,v)对图像进行频率补偿，再进行傅里叶反变换，得到复原后的图像。

维纳滤波图像复原的步骤如下：

1)根据1.1节求出的垂轨和沿轨方向MTF曲线，求出0至奈奎斯特频率(Nyquist frequency,NF)处的MTF矩阵；

2)将MTF矩阵分别进行90°,180°和270°翻转，得到完整的MTF矩阵，再根据式(7)求出维纳滤波器算子Hw(u,v)；

3)对原图像进行二维傅里叶变换，将维纳滤波器算子与频域图像相乘；

4)对结果图像进行二维傅里叶反变换，得到复原后的图像。

2 实验过程与结果分析

2.1 实验过程

用于计算MTF的实验数据是GF-2卫星于2015年3月29日获取的河南嵩山定标场的0级全色图像，并且数据未做过辐射校正处理(图1)。

图1 靶标图像

从图1中分别选择沿轨方向和垂轨方向的刃边目标。根据1.1节中MTF计算步骤，分别求出GF-2卫星全色相机在沿轨方向和垂轨方向的MTF曲线。以沿轨刃边目标为例，提取出的ESF曲线如图2所示。

图2 ESF曲线

对ESF进行微分，并归一化，得到LSF曲线(图3)。

图3 LSF曲线

从图3可以看出，由于像元灰度值的不均匀性，在LSF曲线的两端有明显的翘尾现象，会影响MTF计算精度，因此需要对LSF曲线进行截取。在本文中，截取的像元宽度为8个像元。对截取后的LSF曲线需要用汉明窗进行处理，以消除傅里叶变换时频谱泄露的影响，处理结果如图4所示。

图4 截取后的LSF曲线

截取后的LSF曲线像元宽度决定了MTF曲线在NF处之前的采样点个数。本文截取像元宽度为8，则MTF曲线采样点个数为4，结果如图5所示。

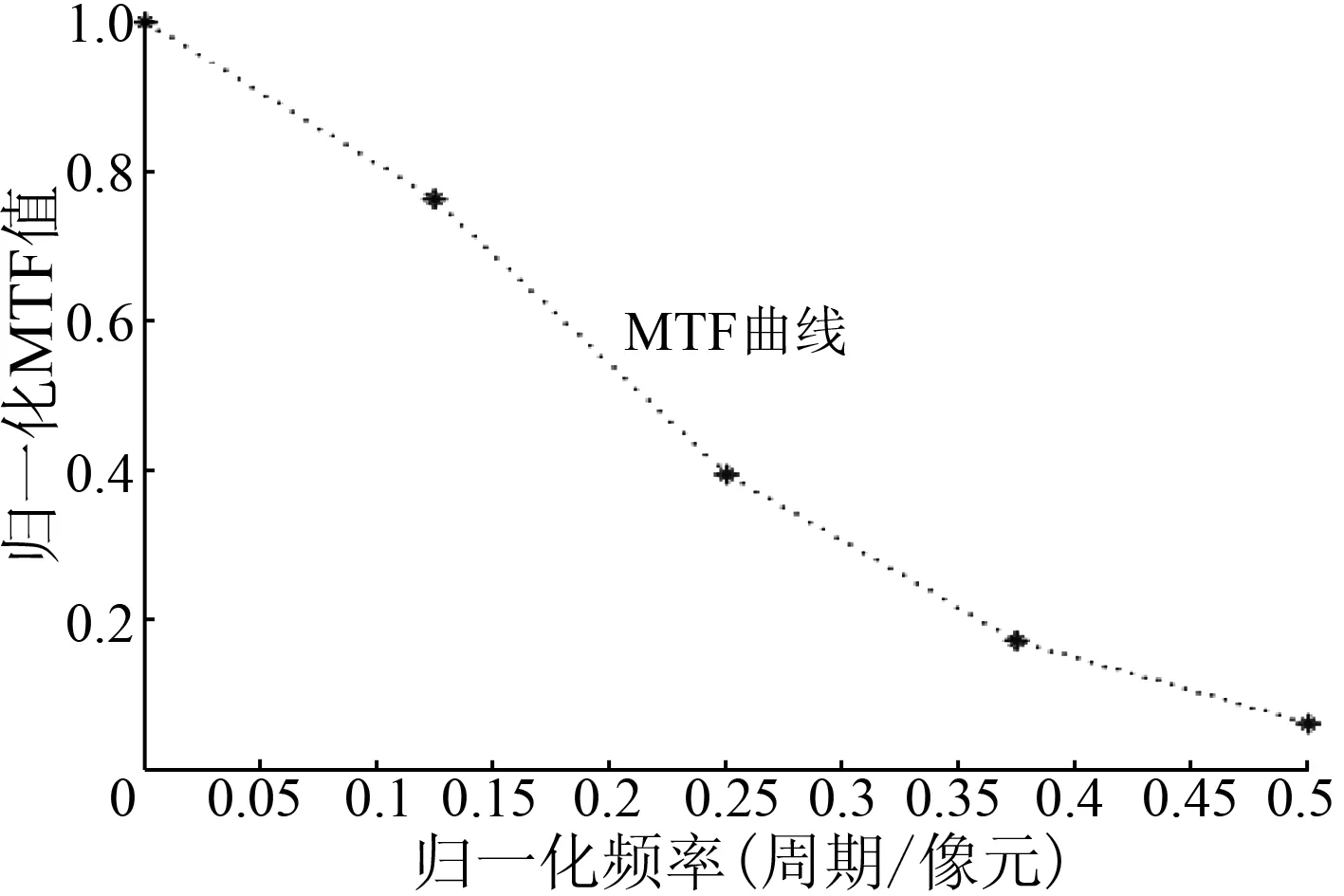
图5 未补0的MTF曲线

从图5可见，由于采样密度不高，MTF曲线并不光滑，与真实的MTF数值有较大的偏离，会影响后续的图像复原处理。如果对截取后的LSF曲线两端补0，则可以增加采样点的个数[2]。本文方法对截取后LSF曲线进行补0，使LSF曲线的像元宽度大幅度增加(图6)。

图6 补0后的MTF曲线

经比较，图6中MTF曲线的采样密度比图5提高了5倍。因此，图6中的MTF曲线更加平滑，有利于提高MTF的数值精度。

同理，可以求出垂轨方向的MTF向量。由于2个方向上的MTF向量值存在差异，如果直接对沿轨方向和垂轨方向的MTF进行向量相乘求解MTF矩阵，则45°方向上的MTF值与沿轨和垂轨方向的MTF值相差很大，会影响到MTF矩阵的数值精度。因此，本文采用葛苹等[6]提出的插值方法求解MTF矩阵。先将沿轨和垂轨2个方向的NF处MTF值的平均值衰减10%，作为45°方向上NF处的MTF值； 再根据沿轨和垂轨方向上的MTF向量的比例关系进行插值。根据对称性，只需先求出0至NF处的MTF矩阵，再分别翻转90°,180°和270°，得到完整的MTF矩阵。

利用计算得到MTF矩阵对图像进行维纳滤波法复原。实验数据是2015年3月29日获取的河南某地区GF-2图像。复原前图像如图7(a)所示，利用传统刀刃法(图7(b))和本文刀刃法(图7(c))分别求得MTF矩阵复原后的图像。

(a) 复原前 (b) 传统刀刃法复原后 (c) 本文刀刃法复原后

图7 不同方法计算MTF矩阵复原前后图像

Fig.7 Images before and after restoration using MTF matrix calculated by different methods

2.2 结果分析

在计算用于图像复原处理的MTF矩阵之前，需要根据待复原处理图像的尺寸，对2.1节计算所得的MTF曲线进行重新插值，以获得新的MTF曲线(图8)。此计算过程中，过低的MTF曲线采样密度会影响插值精度。

图8 2种方法计算的MTF曲线数值精度比较

从图8可以看出，2条曲线的MTF数值存在一定差异，使用本文刀刃方法得到的MTF曲线比传统刀刃方法的MTF曲线显得更为平滑。2种方法计算的MTF值误差见图9。

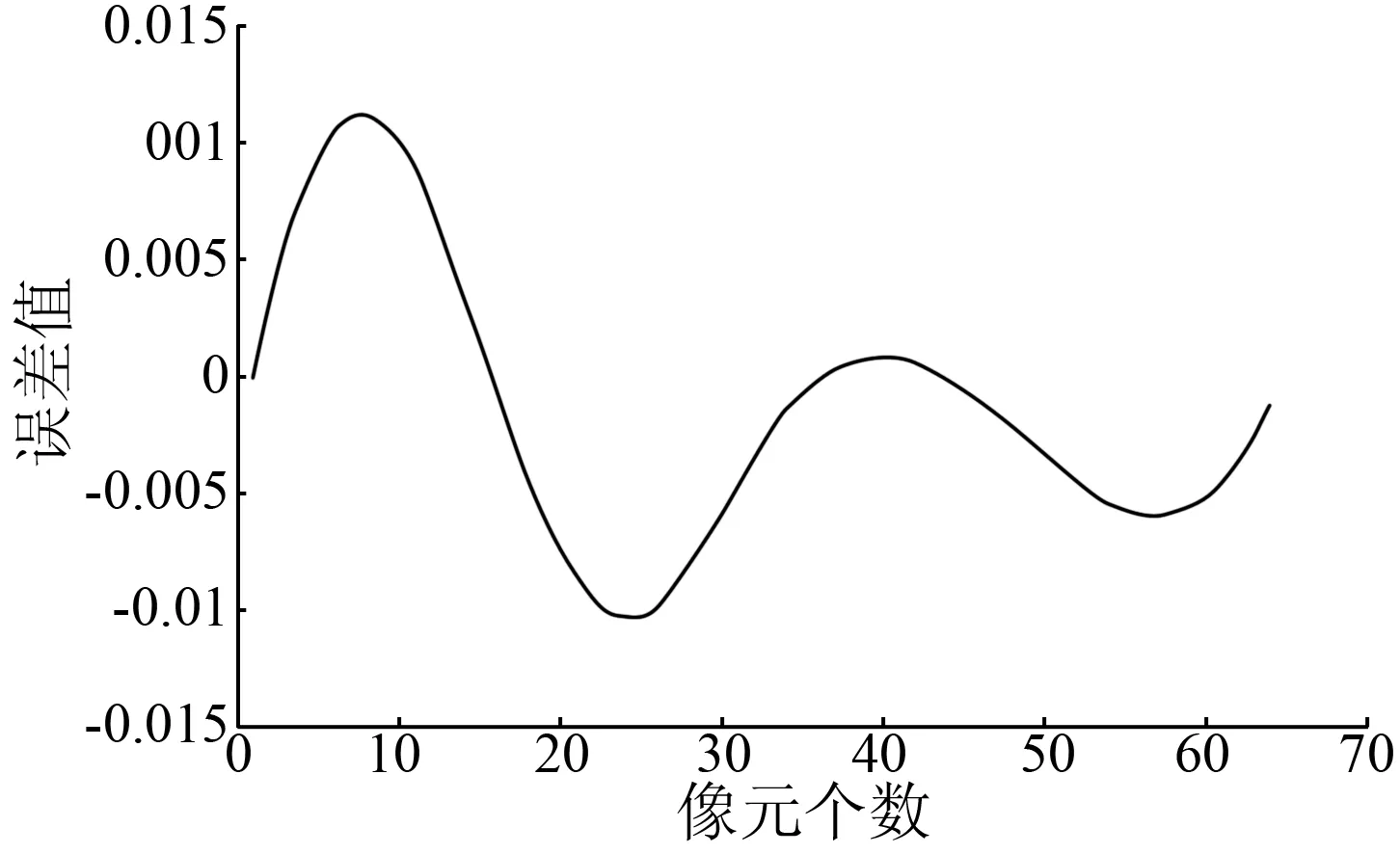
图9 2种方法计算的MTF数值误差

如图9所示，2条曲线的MTF数值误差表现为阻尼震荡，最大误差值为0.01； 随着频率的升高，误差范围逐渐降低。因此，本文刀刃方法提高了计算MTF结果的数值精度。

从主观视觉角度比较复原前、后图像后可以看出，使用本文刀刃法和传统刀刃法计算MTF结果的2种复原后图像的质量均比复原前图像有一定提高，边缘细节增强，对比度提高，细节更清晰。但2种复原后图像的质量差别不明显。

为了定量化分析图像复原处理的效果，本文还使用均值、均方差、熵、空间频率、对比度、边缘能量和平均梯度等7个图像质量指标参数评价复原前、后的图像质量。

1)图像的均值是统计图像的像元灰度平均值，对人眼反映为平均亮度，即

(8)

式中F(i,j)为像元灰度值；M和N分别为图像的行和列。

2)图像的均方差反映了图像的像元灰度离散情况，用来评价图像反差的大小(即包含空间信息的多少)，即

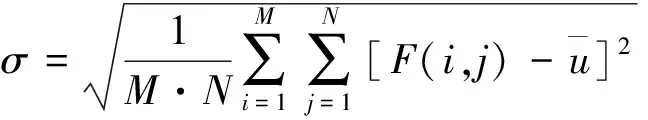
(9)

3)图像的熵是指图像包含信息量的多少，可反映纹理信息的丰富程度，即

(10)

式中P(i)为像元的概率密度。

4)图像的空间频率反映了图像的空间总体活跃程度，其计算公式为

(11)

5)图像的对比度反映图像纹理的清晰程度。对比度越大，说明图像的灰度分布越不均匀，图像越清晰。通常使用0°,45°,90°和135°这4个方向的灰度归一化矩阵，分别求解出4个方向的对比度。其计算公式为

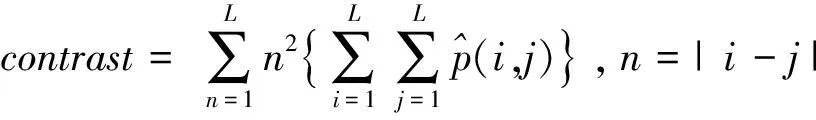
(12)

6)图像的边缘能量反映了图像关于形状特征和细节的重要边缘信息。边缘是高频信息，不同于噪声，带有方向性，可通过各向异性的滤波器来提取。通常使用45°和135°这2个归一化边缘算子

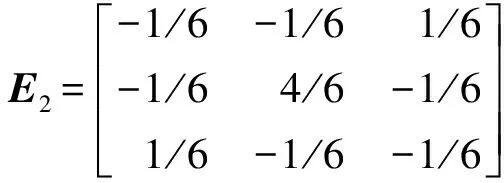
(13)

式中:f(i,j)为像元亮度值；M×N为滤波窗口大小； *为卷积运算符。

7)图像的平均梯度反映图像中微小细节的反差和纹理变化特征，梯度值越大，图像越清晰，其计算公式为

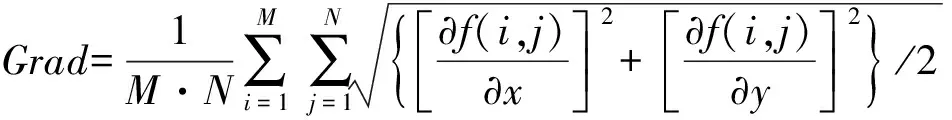
(14)

表1列出复原前、后图像指标参数的比较结果。

表1 复原前后图像质量参数比较

从表1可以看出，复原前、后图像的在均值、均方差、熵和空间频率等图像信息量指标参数上相差不大，说明复原前后图像的信息量没有明显改变。但这2种方法复原后的图像在对比度、边缘能量和平均梯度等图像清晰度指标参数上却有较大的提高，说明2种方法复原后图像的对比度增强，地物边缘处更清晰，细节更丰富，使图像质量有了较大改善。通过比较进一步发现，使用本文刀刃法计算MTF结果得到的复原图像在对比度、边缘能量、平均梯度等指标参数上均优于传统刀刃法。可见，本文刀刃法可以比传统刀刃法得到精度更高的MTF结果，从而进一步提高了图像复原处理的效果。

3 结论

1)在使用刀刃法对GF-2卫星的全色相机进行在轨MTF测量时，本文先使用汉明窗对裁剪后的LSF曲线进行处理，减少频谱泄露的影响； 再对LSF曲线两端补零，增加傅里叶变换后MTF曲线的采样频率。通过实验分析，本文方法求得的MTF曲线比传统刀刃法提高了5倍的采样频率，使得MTF曲线更为平滑。

2)实验结果证明，在使用维纳滤波法对GF-2卫星影像复原时，本文方法可以提高维纳滤波器所需MTF矩阵的数值精度，使得复原图像在对比度、边缘能量和空间频率等代表图像清晰度的关键指标上均优于传统方法，提高了图像复原质量。

[1] 顾行发,李小英,闵祥军,等.CBERS-02卫星CCD相机MTF在轨测量及图像MTF补偿[J].中国科学E辑工程与材料科学,2005,35(s1):26-40. Gu X F,Li X Y,Min X J,et al.In flight MTF monitoring and compensation for CCD camera on CBERS-02[J].China Science Series E Engineering & Materials Science,2005,35(s1):26-40.

[2] 王先华,乔延利,易维宁.卫星光学相机MTF在轨检测方法研究[J].遥感学报,2007,11(3):318-322. Wang X H,Qiao Y L,Yi W N.In-flight measurement of satellite optical camera MTF[J].Journal of Remote Sensing,2007,11(3):318-322.

[3] 蔡新明.基于卫星遥感图像的MTF计算和分析[D].南京:南京理工大学,2007:15-18. Cai X M.Calculation and Analysis of MTF Based on Satellite Remote Sensing Image[D].Nanjing:Nanjing University of Science and Technology,2007:15-28.

[4] 陈强,戴奇燕,夏德深.基于MTF理论的遥感图像复原[J].中国图象图形学报,2006,11(9):1209-1305. Chen Q,Dai Q Y,Xia D S.Restoration of remote sensing images based on MTF theory[J].Journal of Image and Graphics,2006,11(9):1209-1305.

[5] 柴雅琼,冯钟葵,齐东楷,等.改进的MTF遥感影像复原算法研究[J].遥感信息,2012(1):78-83. Chai Y Q,Feng Z K,Qi D K,et al.An improved MTFC restoration algorithm for remote sensing image[J].Remote Sensing Information,2012(1):78-83.

[6] 葛苹,王密,潘俊,等.高分辨率TDI-CCD成像数据的自适应MTF图像复原处理研究[J].国土资源遥感,2010,22(4):23-28.doi:10.6046/gtzyyg.2010.04.06. Ge P,Wang M,Pan J,et al.A study of adaptive MTF image restoration of high resolution TDI-CCD image data[J].Remote Sensing for Land and Resources,2010,22(4):23-28.doi:10.6046/gtzyyg.2010.04.06.

[7] 孟伟,金龙旭,李国宁,等.调制传递函数在遥感图像复原中的应用[J].红外与激光工程,2014,43(5):1690-1696. Meng W,Jin L X,Li G N,et al.Application of MTF in remote sensing image restoration[J].Infrared and Laser Engineering,2014,43(5):1690-1696.

[8] 张凡.基于改进NAS-RIF算法的遥感噪声图像自适应复原[J].国土资源遥感,2015,27(2):105-111.doi:10.6046/gtzyyg.2015.02.17. Zhang F.Self-adaptive restoration for remote sensing noise images based on improved NAS-RIF algorithm[J].Remote Sensing for Land and Resources,2015,27(2):105-111.doi:10.6046/gtzyyg.2015.02.17.

[9] 徐航,李传荣,李晓辉,等.一种优化的刃边法MTF在轨评估算法[J].遥感信息,2012,27(6):10-16. Xu H,Li C R,Li X H,et al.An optimized knife-edge algorithm for on-orbit MTF estimation[J].Remote Sensing Information,2012,27(6):10-16.

(责任编辑： 刘心季)

三维立体中国土地利用图正式出版发行

为了积极响应党中央、国务院和国土资源部领导的号召，利用好第二次全国土地调查的数据成果，充分展现我国土地利用现状，满足多元化和人性化的地理空间信息服务需求，中国大地出版社(地质出版社)利用当今最先进的三维立体技术将地形特征信息与土地利用专题图有机结合，集成了地理信息系统、三维立体制图技术、CTP数字制版技术、光栅材料及特种印刷技术，科学、直观地反映土地利用的空间分布规律、发展变化过程；多角度、多比例尺、全面系统地展现全国、省、市(县)各级行政单位的土地利用调查研究成果。将三维立体技术应用到土地利用系列图上，突破了传统地图制图中纸质载体单一的局限性，实现裸眼三维立体土地利用现状的可视化效果。

三维立体图手摸上去是平的，眼看上去是立体的，有突出的前景和深邃的后景，是一种全新的视觉体验和数据产品模式。利用特种光学材料对地图进行专业印刷及装帧，生成画面色彩逼真、光亮、层次感强、画质细腻的三维立体图，具有极强的立体感和纵深感。

一幅完美的三维立体图是由多个图层组成，视觉上层次分明、色彩鲜艳，给人以真实、栩栩如生、身临其境的感觉，具有很强的视觉冲击力和很高的艺术欣赏价值。

中国大地出版社(地质出版社)对三维立体中国土地利用系列图的开发与应用具有完整的知识产权。

地址： 北京市海淀区学院路31号

电话： 010-66552766 66554569

http: //www.gph.com.cn

(张立光)

On-orbit MTF estimation and restoration of GF-2 satellite image

WANG Zhizhong1,2， ZHANG Qingjun1

(1.ChinaInstituteAerospaceScienceandTechnology，Beijing100086，China； 2.ChinaCentreofEarthResourceSatelliteDataandApplication，Beijing100094，China)

Modulation transfer function(MTF)is not only an efficient method for monitoring the on-orbit satellite operation status and performance but also an important parameter which is often used to restore satellite image. In this paper, the knife edge method was used to measure the on-orbit MTF of GF-2 satellite panchromatic camera. During the calculation of MTF, Hamming window was used in the process of clipping the line spread function(LSF)in order to restrain the leak of frequency spectrum. Besides, the authors expanded the LSF with zeros so as to improve the sampling frequency during the Fourier transform. The experimental results show that the sampling density of MTF using the knife edge method proposed in this paper is 5 times more than that of the traditional method and the MTF curve is also smoother compared with that of the traditional method. Therefore, the more accurate MTF matrix value can be obtained to improve the performance of image restoration by this method. In this paper, the Wiener filtering method was used to restore the GF-2 satellite panchromatic image with the MTF matrix value. The experimental results also show that the MTF matrices computed by the two methods can all improve the clearness and object edge information of the image. However, the image restored by the MTF matrix values of the authors’ method is superior to that of the traditional method in such characteristics as contrast, edge energy and average gradient.

GF-2 satellite；on-orbit MTF estimation；knife edge method；image restoration；Wiener filtering

10.6046/gtzyyg.2016.04.15

王治中,张庆君.GF-2星全色相机在轨MTF测量和图像复原研究[J].国土资源遥感,2016,28(4)：93-99.(Wang Z Z,Zhang Q J.On-orbit MTF estimation and restoration of GF-2 satellite image[J].Remote Sensing for Land and Resources,2016,28(4)：93-99.)

2015-06-23；

2015-07-28

国家科技部对外科技合作项目“中国―东盟遥感卫星数据共享服务平台”(编号： 2012DFF10060)和国家高分辨率对地观测系统重大专项“高分二号卫星工程”(编号： 科工高分2012836号)共同资助。

TP 751.1

A

1001-070X(2016)04-0093-07

王治中(1981-),男,博士研究生,高级工程师,主要研究方向为遥感卫星地面系统总体设计、遥感图像处理及融合。Email： wangzz04@126.com。

张庆君(1969-),男,研究员,总设计师,主要从事遥感卫星总体设计等方面的研究。Email： ztzhangqj@163.com。