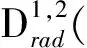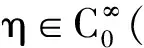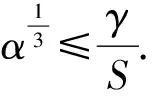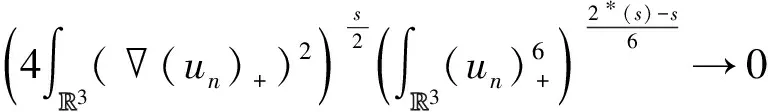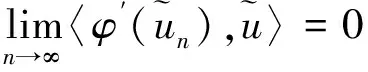R3 双临界Kirchhoff型方程正解的存在性

宋雅倩， 张福伟， 刘进生

(太原理工大学 数学学院， 山西 太原 030024)



R3双临界Kirchhoff型方程正解的存在性

宋雅倩， 张福伟， 刘进生

(太原理工大学 数学学院， 山西 太原 030024)

利用变分方法研究了R3上具有双临界非线性项的Kirchhoff型方程正解的存在性. 首先证明了该问题的能量泛函满足山路引理的几何条件，从而证明了能量泛函存在(PS)c序列，进而通过(PS)c序列的有界性与弱极限的非平凡性及径向对称空间的性质证明了此(PS)c序列具有强收敛子列，因此证明了能量泛函存在非平凡临界点，于是此问题存在非平凡解，最后证明了此非平凡解是正解.

Kirchhoff型方程； 双临界非线性项； 山路引理； 正解

0 引 言

本文主要考虑以下双临界Kirchhoff型方程

解的存在性. 其中常数a,b>0,2*= 6, 2*(s)=6-2s,s∈(0,1). 而

D1,2(R3)={u∈L2*(R3)|u∈L2(R3)},

其内积与范数分别为

〈u,v〉=∫R3u·v,

由于Kirchhoff型方程的重要性，近年来，很多学者研究了如下的Kirchhoff型问题[1-8]

非平凡解的存在性. 同时，也有学者研究带有Sobolev临界指数的Kirchhoff 型方程[9-13]

文献[14]运用山路引理证明了RN中双临界p-Laplace方程

定理 1 对任意a,b>0,s∈(0,1), 方程(1)在D1,2(R3)中至少存在一个正解.

1 主要结果的证明

在径向空间

R3)={u∈D1,2(R3)|u(x)=u(|x|)}

中考虑问题(1). 由文献[14]知

引理 1 能量泛函φ满足山路引理的几何条件. 即

1)φ(0)=0， 并且存在α,ρ>0， 当‖u‖=ρ时， 有φ(u)≥α>0.

注意到2*(s)=6-2s,s∈(0,1)， 从而存在α,ρ>0， 当‖u‖=ρ时， 有φ(u)≥α>0.

从而存在充分大的t0>0， 使得‖t0u‖>ρ且φ(t0u)<0. 令e=t0u， 则‖e‖>ρ且φ(e)<0.

φ(γ(1))<0},

即{un}是泛函φ的一个(PS)c序列.

为了证明φ满足(PS)c条件， 本文在引理2～引理8中研究了(PS)c序列的结构.

引理 2 若{un}为φ的(PS)c序列， 则{un}有界.

证明 由于φ(un)→c,φ′(un)→0且4<2*(s)<6， 则

故{un}有界.

对任意的0

A={x∈R3|r≤|x|

C2∫A|vn-v|2→0,

∫R3|un||(η2)||un|≤

式中：C(η)为正常数[14].

∫R3|(η un)|2=∫R3|ηun|2+o(1).

由引理2， {un}有界. 故

〈φ′(un,η2un〉=o(‖η2un‖)=o(‖un‖)=

o(1), n→∞.

由式(5)～式(8)得

o(1)=〈φ′(un),η2un〉=a∫R3|(η un)|2+

b∫R3|un|2∫R3|(η un)|2+o(1),

从而

‖η un‖2=o(1),

对任意的δ>0， 令

由引理4可知， α,β,γ的取值与δ无关.

o(1)=

a∫Bδ(0)|un|2+b∫R3|un|2∫Bδ(0)|un|2-

从而

a∫Bδ(0)|

由α,β,γ定义可知αγ≤α+β. 于是结论成立.

所以

这与引理7矛盾.

,φ〉=∫R3aφ+

bB2∫R3φφ.

所以

bB2∫R3|

矛盾. 故∫R3|||2， 即又由于

b∫R3||2∫R3

[1]Sun J J, Tang C L. Resonance problems for Kirchhoff type equations[J]. Discrete and Continous Dynamical Sys., 2013(5): 2139-2154.

[2]Cheng B T. New existence and multiplicity of nontrivial solutions for nonlocal elliptic Kirchhoff type problems[J]. J. Math. Anal. Appl., 2012, 394: 488-495.

[3]Cheng B T, Wu X. Existence results of positive solutions of Krichhoff problems[J]. NonlinearAnal., 2009(71): 4883-4892.

[4]Yang Y, Zhang J H. Nontrivial solutions of a class of nonlocal problems via local linking theory[J]. J. Appl. Math. Lett., 2010(23): 377-380.

[5]Sun J, Liu S B. Nontrivial solutions of Kirchhoff type problems[J]. J. Applied Mathematics Letters, 2012, 25: 500-504.

[6]Li Y H, Li F Y, Shi J P. Existence of a positive solution to Kirchhoff type problems without compactness conditions[J]. J. Differential Equations, 2012, 253: 2285-2294.

[7]Liang Z P, Li F Y, Shi J P. Positive solutions to Kirchhoff type equations with nonlinearity having prescribed asymptotic behavior[J]. Ann. I. H. Poincaré-AN, 2014, 31(1): 155-167.

[8]He X M, Zou W M. Existence and concentration behavior of positive solutions for a Kirchhoff equation in R3[J]. J. Differential Equations, 2012, 252: 1813-1834.

[9]Li G B, Ye H Y. Existence of positive solutions for nonlinear Kirchhoff type problems in R3with critical Sobolev exponent[J]. Mathematical Methods in the Applied Sciences, 2014, 37(16): 2570-2584.

[10]Figueiredo G M. Existence of a positive solution for a Kirchhoff problem type with critical growth via truncation argument[J]. J. Math. Anal. Appl., 2013, 401: 706-713.

[11]Xu J X, Zhang F B. Multiplicity and concentration of positive solutions for a Kirchhoff type problem with critical growth[J]. J. Differential Equ., 2012(253): 2314-2351.

[12]Brezis H, Nirenberg L. Positive solutions of nonlinear elliptic problems involving critical Sobolev exponent[J]. Comm. Pure Appl. Math., 1983, 36: 437-477.

[13]Alves C O, Correa F J S A, Figueiredo G M. On a class of nonlocal elliptic problems with critical growth[J]. Differ Equ. Appl., 2012(2): 409-417.

[14]Roberta F, Patrizia P, Ferdric R. On a p-Laplace equation with multiple critical nonlinearities[J]. Journal De Mathematiques Purest Appliquees, 2009, 91: 156-177.

[15]Badiale M, Serra E. Semilinear elliptic equations for beginners[J]. Springer London, 2011: 226.

Existence of Positive Solutions for Kirchhoff Type Problems in R3with Multiple Critical Nonlinearities

SONG Ya-qian, ZHANG Fu-wei, LIU Jin-sheng

(College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China)

The existence of positive solutions for Kirchhoff type problem with multiple critical nonlinearities was investigated by using variational method. Firstly, it was proved that the energy functional possessed mountain pass geometry and got a (PS)csequence.Then, it was demonstrated that the (PS)csequence contained strong convergent subsequence through the boundedness of the (PS)csequence, the non triviality of weak limit, and the property of radial symmetry space. Therefore, the energy functional has at least one nontrivial critical point and the problem has at least one nontrivial solution. Consequently, it is achieved that the nontrivial solution is positive.

Kirchhoff type problem; multiple critical nonlinearities; mountain pass theorem; positive solution

1673-3193(2016)06-0576-05

2016-05-28

宋雅倩(1990-)， 女， 硕士生， 主要从事非线性泛函分析研究.

张福伟(1957-)， 女， 副教授， 主要从事非线性泛函分析研究.

O175.2

A

10.3969/j.issn.1673-3193.2016.06.005