基于GM-SVM的边境封控油料保障需求预测

倪 聪，周庆忠，刘 磊，魏小林

(后勤工程学院 军事油料应用与管理工程系，重庆 401311)



● 基础科学与技术 Basic Science & Technology

基于GM-SVM的边境封控油料保障需求预测

倪 聪，周庆忠，刘 磊，魏小林

(后勤工程学院 军事油料应用与管理工程系，重庆 401311)

为解决边境封控油料保障需求预测问题，针对油料保障需求不仅呈现线性变化，且蕴含非线性变化规律，传统的单一模型很难同时对线性和非线性规律加以预测的特点，提出一种基于灰色支持向量机(GM-SVM)的边境封控油料保障需求组合预测模型。首先，运用灰色模型对油料保障需求进行预测，挖掘其线性变化规律；然后，采用支持向量机进行预测，描述油料保障需求的非线性变化规律；最后，将两种预测结果进行加权平均，作为边境封控油料保障需求预测的最终结果。预测结果表明，GM-SVM组合预测模型预测精度较高，较好地克服了单一预测模型的缺陷。

油料保障；需求预测；灰色模型；支持向量机

油料保障需求是指为确保部队作战顺利实施而对油品、油料装备、油料保障人员、油料保障机构等的需要[1]。边境封控油料保障需求受到自然地理环境、油料和油料装备水平、油勤人员数质量和行动发起突然、行动样式多变、行动力量多元等因素的影响，变化趋势错综复杂，不但呈现线性变化特点，而且蕴含非线性变化规律，如何准确地预测边境封控行动油料保障需求、及时有效地开展边境封控行动油料保障，越来越受到专家学者和油勤人员的关注。

边境封控行动油料保障需求预测，由于缺乏以往边境封控行动油料保障需求的统计数据，目前此类研究多是基于油料供应标准、任务时间、单位装备人员实力以及油勤人员历史经验推断等进行计算。近年来，也出现了基于灰色系统理论、支持向量机回归、案例推理、粒子群算法、神经网络、马尔科夫模型、改进分段维等的油料保障需求预测模型[2-9]。这些方法均取得较好的预测效果，但对于边境封控油料保障需求预测问题，单一预测模型均不能全面描述其变化规律。为了充分发挥单一预测模型优点，有人提出了油料保障需求预测的组合模型，实践表明，组合模型能较准确地描述油料保障需求变化的特点，是当前油料保障需求预测的主要研究方向。为解决边境封控油料保障需求预测难以量化的问题，本文在借鉴前人已有研究成果的基础上[10-13]，将灰色预测模型(grey model,GM)和支持向量机(super vector machine,SVM)进行融合，提出了一种基于灰色支持向量机(GM-SVM)的边境封控油料保障需求预测模型，并通过算例分析验证了GM-SVM预测模型的可行性及有效性。

1 预测原理

边境封控油料保障需求预测，就是综合考虑边境封控行动任务、有关用油装备数量、行动持续时间以及行动任务环境等因素对油料需求量的影响，对一定时期内边境封控所需油料的流向和流量以及供求规律进行调查研究取得各种资料和信息，采用科学的方法和技术手段，进行分析研究，预计和推测出未来某一阶段内边境封控油料保障需求的变化和发展趋势[14]。

边境封控行动油料保障需求历史数据的时间序列(pt)，受自然环境、油料储备、人员素质和行动突发、样式复杂、力量多元等的影响，具有较强的非线性变化趋势，但是其中隐含着线性变化规律。因此，边境封控油料保障需求数据可以看成两部分组成：

pt=at+bt

(1)

式中：pt为t时刻边境封控油料保障需求；at为线性变化部分油料保障需求；bt为非线性变化部分油料保障需求。

GM和SVM具体组合原理(如图1所示)为：首先，建立GM(1，1)模型对边境封控油料保障需求数据进行预测，描述其中的线性变化部分；然后，采用SVM对隐含其中的非线性变化趋势进行预测；最后，将两种模型预测结果进行加权平均，得到组合模型的油料保障需求预测值。这样充分发挥GM和SVM的各自优势，提高预测的准确与可靠程度。

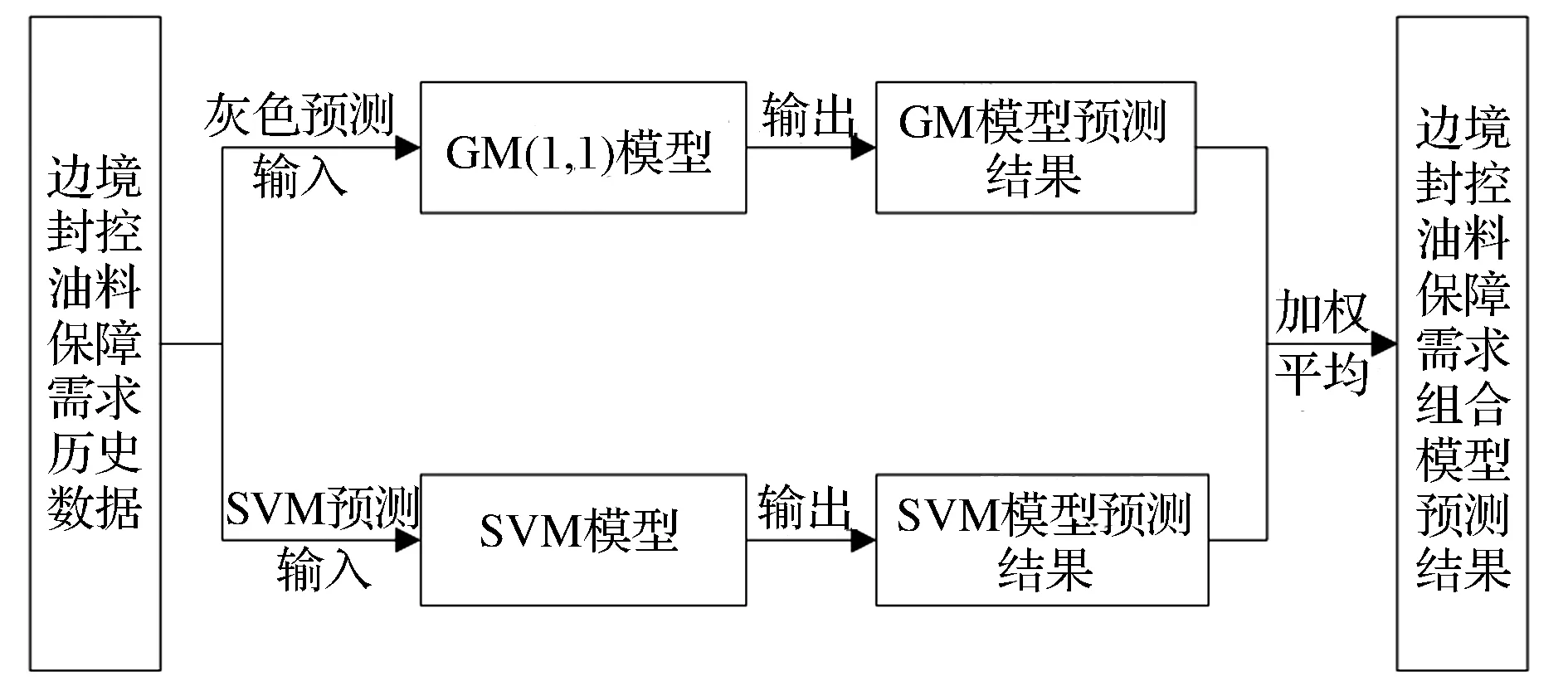
图1 组合模型预测原理

2 边境封控油料保障需求组合预测模型

2.1 传统GM(1,1)模型

GM(1，1)模型即灰色模型(一阶方程、一个变量)，它是一种以灰色模块概念为基础、以微分拟合法为核心的建模方法，主要用于数列预测[15]。

设n个月边境封控油料保障需求历史数据原始序列为

X(0)={x(0)(k),k=1,2,…，n}

(2)

对n个月边境封控油料保障需求数据原始序列进行累加，消除数据的波动性，得到其一阶累加生成(1-AGO)序列为

X(1)={x(1)(1)，x(1)(2)，…，x(1)(n)}

(3)

对X(1)作紧邻均值生成，即对X(1)序列中每组相邻的两个值进行平均得到一组新的值，由此构成一个新的序列为

z(1)(k)=0．5x(1)(k)+0．5x(1)(k-1)

k=2，3，…,n

(4)

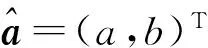
(5)

其时间响应序列为

k=1，2，…,n

(6)

将其还原可得预测方程：

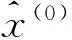
(7)

边境封控油料保障需求经过GM(1，1)模型预测后，其线性变化趋势可以得到描述，但是无法对其非线性变化趋势加以预测，因此采用支持向量机对油料保障需求非线性变化趋势进行预测，以提高预测精度。

2.2 支持向量机模型

支持向量机(super vector machine, SVM)是基于统计学习理论的VC维理论和结构风险最小原则发展起来的一种小样本学习方法，具备较强的非线性建模能力，最早由Vapnik[14]提出，主要分为支持向量分类机和支持向量回归机。边境封控油料保障需求预测需要利用支持向量回归机的相关原理和算法，其核心思想是在用内积函数描述非线性变换的基础上，将低维空间转换到高维空间，并在高维空间中找寻输入、输出变量的非线性关系[16]，目的是通过最小化目标函数来确定回归函数。

设n个月边境封控油料保障需求历史数据原始序列为{x(1),x(2),…，x(n)}，支持向量机的回归原理可表述为：寻找从输入空间到输出空间上的映射f，使得y=f(x)，从而根据该映射得到输入样本xi对应的输出yi。通过核函数的映射，将边境封控油料保障需求数据映射到高维空间进行线性回归。对于边境封控油料保障需求历史数据，SVM的回归函数为

f(x)=ω·φ(x)+b

(8)

式中：ω为权重向量；φ(x)为输入向量；b为偏置常数。

根据统计学结构风险最小化的原则，通过最小化目标函数来确定回归函数，即

(9)

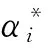
(10)

(11)

求解式(11)二次规划问题，可得边境封控油料保障需求支持向量机预测函数为

(12)

目前，常用于支持向量机的核函数主要有3种[15，17]，考虑到径向基核函数(radial basis function,RBF)只需要确定一个变量，且利用其构造的支持向量机训练参数相对较少，因此，本文选择其作为SVM核函数，RBF核函数定义为

(13)

式中σ为径向基核函数宽度系数。

2.3 组合模型建立

GM-SVM组合模型可以描述为

(14)

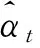
3 算例分析

3.1 数据的选取及预处理

表1为从油料信息管理系统中选取并脱密处理得到的某部队遂行边境封控演习的24组(以月为单位)油料保障需求历史数据。

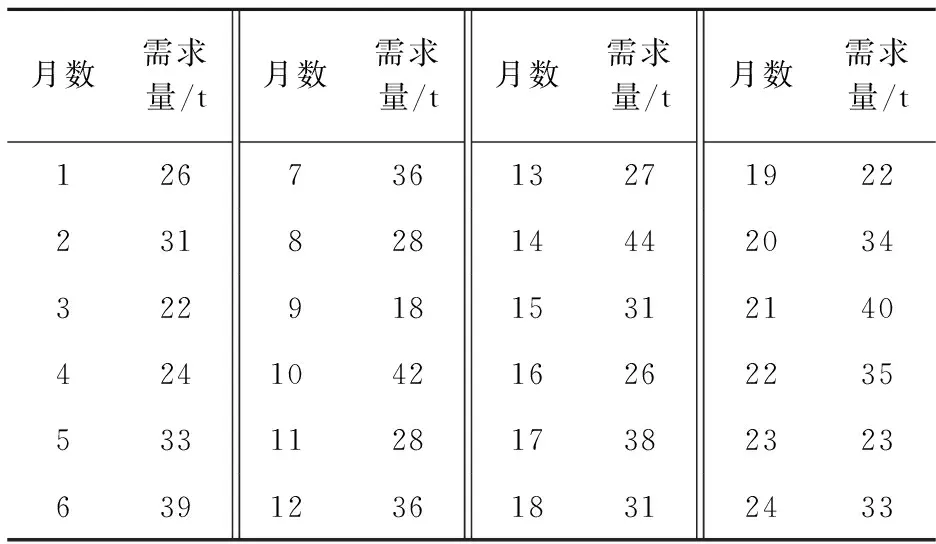
表1 某部队遂行边境封控演习油料保障(油品)需求量

由于边境封控油料保障受到诸多复杂影响因素的影响，油料保障需求历史数据也存在很大波动，为消除最大最小值之间巨大差异对建模的不利影响，将样本数据采用极值法进行归一化处理：

(15)

经过式(15)的处理，就把所有样本数据归一化后统一到了集合[0,1]下。

3.2 边境封控油料保障需求预测

利用Matlab 7.0仿真软件自编了GM(1，1)模型求解程序，将表1中前20组(1—20月)的边境封控油料保障需求历史数据经归一化预处理后，作为训练集在GM(1，1)模型中进行训练并拟合。边境封控油料保障需求GM(1，1)模型的预测拟合值与实际需求值的对比如图2所示。

图2 GM(1,1)模型的训练集拟合曲线

由图2可知，GM(1，1)模型对训练集的预测结果与实际需求值相比整体趋势比较一致，但是9、10、15、17月4组预测拟合值仍存在较大偏差。

利用Matlab 7.0的Lib-SVM工具箱将表1中前20组的边境封控油料保障需求历史数据重构成多维时间序列，然后将其输入到SVM模型进行学习，得到SVM模型参数C=8、σ=0.088，重新对训练集进行学习，并对其进行拟合，得到的边境封控油料保障需求SVM模型的预测拟合值与实际需求值的对比如图3所示。

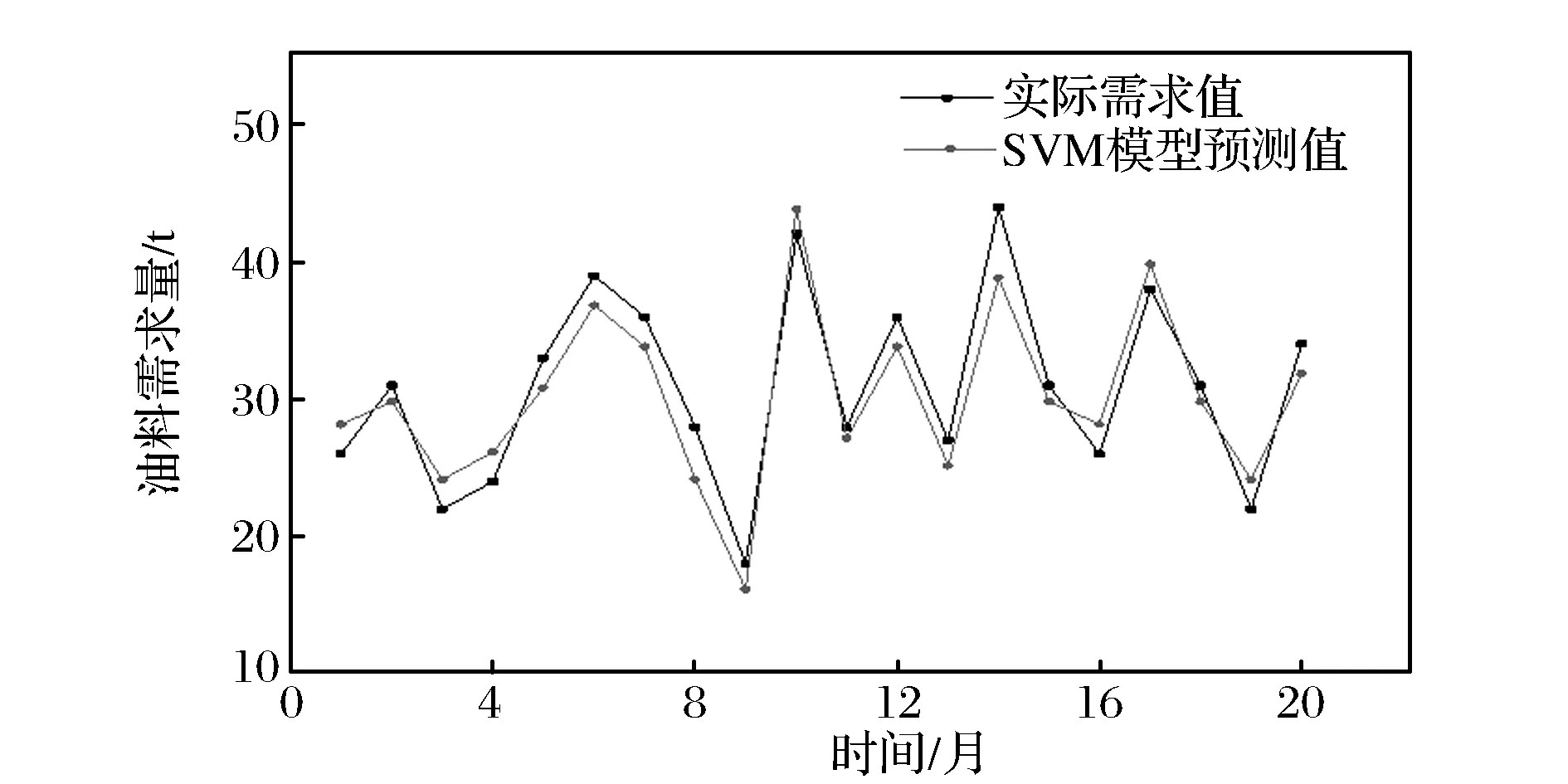
图3 SVM模型的训练集拟合曲线

由图3可知，SVM模型对训练集的预测结果较好地预测出了样本数据的非线性变化趋势，但是3、6、14月3组预测拟合值仍存在较大波动。

对GM(1，1)模型和SVM模型的预测结果进行加权平均，利用数学规划法确定加权系数λ1=0.25、λ2=0.75，从而得到GM-SVM组合模型。然后将表1中后4组(21—24月)的边境封控油料保障需求历史数据作为测试集。分别利用GM(1，1)模型、SVM模型和GM-SVM组合模型对测试集进行预测，得到的预测拟合值如图4所示。

图4 不同预测模型的测试集拟合曲线

由图4可知，与单一GM(1，1)模型、SVM模型相比，GM-SVM组合模型预测结果与实际需求值之间的偏差明显更小。这主要是由于GM-SVM组合模型集中发挥了单一预测模型各自的优势，提高了边境封控油料保障需求的预测精度。对比结果初步证明，GM-SVM组合模型可以较为准确地预测边境封控油料保障需求。

3.3 预测结果评价

为了综合评价边境封控油料保障需求预测结果的可靠性和准确性，引入以下评价指标：

(16)

(17)

式中：MAPE为平均相对误差；MSE为均方差。

利用上述评价指标对3种模型预测结果进行评价(见表2)。

表2 不同模型预测结果比较

由表2可知，对于平均相对误差和均方差两个评价指标，GM-SVM组合模型均明显小于单一GM(1，1)模型或SVM模型，表明组合模型能够更为准确可靠地预测边境封控油料保障需求。

4 结 语

对于动态变化中的边境封控行动油料保障需求，传统单一非线性或线性预测模型难以得到理想的预测结果。为此，本文提出了一种基于灰色

支持向量机(GM-SVM)的边境封控油料保障需求组合预测模型。预测结果表明，GM-SVM组合预测模型不仅发挥了GM(1，1)模型的线性预测能力，又发挥了支持向量机的非线性预测能力，可以较为准确地描述油料保障需求变化趋势，为边境封控油料保障需求预测提供了一个较好的思路。

[1] 丁国勤.军队油料保障指挥决策模型研究[D].重庆:重庆大学,2008:21-22.

[2] 周庆忠,曾慧娥.基于改进微粒群神经网络的油料储备预测[J].计算机仿真,2013(9):314-315.

[3] 王冰,周庆忠,刘岩,等.油料保障预测系统中案例推理方法[J].计算机系统应用,2012(4):75-78.

[4] 李伟,王红旗,严乔乔.BP神经网络:马尔科夫模型在军用油料消耗预测中的应用研究[J].中国储运,2012(1):131-132.

[5] 夏秀峰,刘权羲.基于灰色神经网络的装甲部队油料消耗预测[J].火力与指挥控制,2014(4):95-99.

[6] 崔浩,周庆忠.基于神经网络的信息化战争油料保障指挥决策模型优化研究[J].物流技术,2010(11):152-155.

[7] 陆思锡,周庆忠,熊彪.基于支持向量机的舰艇部队作战油料消耗量预测研究[J].物流技术,2013(5):477-479.

[8] 樊荣,朱才朝,陆思锡,等.支持向量机在航空兵部队油料消耗量预测中的应用[J].重庆大学学报,2012(6):41-45.

[9] 李必鑫,黄金,林世岗.基于改进分段维的油料保障需求预测模型[J].中国储运,2012(10):131-132.

[10] 杨梅,李广.油料保障需求预测模型的仿真研究[J].计算机仿真,2013(10):382-385.

[11] 杨焕海.人才需求组合预测的建模与仿真分析[J].计算机仿真,2013(10):253-256.

[12] 陈荣江,张芳,罗批,等.石油模型研究综述[J].计算机仿真,2013(6):4-10.

[13] 张丽.农村劳动力迁移对经济影响模型分析[J].计算机仿真,2015(2): 227-230.

[14] 陆思锡.海军舰艇部队作战油料保障决策理论与应用研究[D].重庆:后勤工程学院,2013:55-65.

[15] 胡振.GM(1,1)数据融合预测模型研究与仿真[J].计算机仿真,2013(6):356-360.

[16] 黎武,冯平,李九林,等.基于重构相空间AD-SVM的短期电力负荷预测[J].后勤工程学院学报,2014，30(6):72-77.

(编辑：张峰)

Demand Forecast for POL Support in Border Blockage and Control Based on GM-SVM

NI Cong, ZHOU Qingzhong, LIU Lei, WEI Xiaolin

(Military Oil Application and Management Engineering Department, Logistics Engineering University,Chongqing 401311, China)

In order to solve the problem of demand forecast for POL support in border blockage and control, considering that POL support demand has the characteristic of linear variation and nonlinear variation and traditional single model couldn’t forecast linear and nonlinear variation simultaneously, the paper puts forward a demand forecast model for POL support in border blockage and control based on GM-SVM. Firstly, it forecasts the POL support demand with grey model and excavates its linear variation rule. Then, it forecasts POL support demand with SVM and describes its nonlinear variation rule. Finally, it takes a weighted average on the two forecast results and obtains the final demand forecast result for POL support in border blockage and control. The result shows that the forecast model based on GM-SVM has high forecast accuracy and can overcome shortcoming of single forecast model.

POL support; demand forecast; grey model (GM); support vector machine (SVM)

2015-08-23；

2015-12-20． 作者简介： 倪 聪(1987—)，男，硕士研究生； 周庆忠(1961—)，男，教授，博士研究生导师．

10．16807/j.cnki.12-1372/e.2016.03.020

E234

A

1674-2192(2016)03- 0090- 05