第基于保障度的车辆器材周转量单品种数量优化

王 亮，文正中，何 健，吕志明

(1．军事交通学院 军用车辆系,天津 300161； 2．军事交通学院 研究生管理大队，

天津 300161； 3．济南军区 后勤装备维修培训中心，济南 250022)



● 装备保障 Equipment Support

第基于保障度的车辆器材周转量单品种数量优化

王 亮1，文正中2，何 健2，吕志明3

(1．军事交通学院 军用车辆系,天津 300161； 2．军事交通学院 研究生管理大队，

天津 300161； 3．济南军区 后勤装备维修培训中心，济南 250022)

为了能够合理解决车辆器材周转量单品种数量优化问题，依据保障度理论，改进传统的保障度模型，建立了基于保障度的车辆器材周转量单品种数量优化模型，并利用粒子群算法对模型进行求解，同时给出了相关实例进行验证。研究结果表明：利用编程语言设计车辆器材周转量优化系统程序，提高了优化模型的实用性和可操作性；通过对优化结果进行分析，验证了模型的合理性。

车辆器材；周转量；保障度；优化模型；粒子群算法

合理地确定车辆器材周转储备数量对车辆器材运输保障任务的完成具有十分重要的意义。目前，常用确定车辆器材储备数量的方法，无论是统计预测法、比较分析法还是直接计算法都有一定的局限性。如比较分析法只适用于同一类型的车辆装备，所以用此方法确定车辆器材周转量单品种数量较为困难，而直接计算法只适用于需要定期更换的耗损类器材。鉴于此，本文分析了传统保障度模型的不足，依据保障度理论，改进传统的保障度模型，建立了基于保障度的车辆器材周转量单品种数量优化模型，并利用粒子群算法对模型进行求解，同时给出了相关实例进行验证。

1 相关概念

1．1 车辆器材保障度

车辆器材保障度，是指单位时间内该品种车辆器材实际保障的数量占需求保障数量的百分比[1]。通常按下式计算：

L=EiR(Xi)×100%

(1)

式中：L为车辆器材保障度；i为车辆器材种类,i=1，2，…，N；Xi为第i种车辆器材的储备数量；Ei为第i种车辆器材需求量占所有品种车辆器材总需求量的比值，由于车辆器材的需求量随机，所以Ei也可以表示为第i种车辆器材的期望消耗量与所有车辆器材的期望消耗量的比值；R(Xi)为储备量为Xi时该车辆器材的可靠度。

针对某一品种车辆器材而言，由于其需求量比例Ei=1，因此保障度仍等于该品种车辆器材的可靠度。用供应水平来定义车辆器材周转量系统的保障度，是对部队车辆器材保障单位供应保障水平的评价，并不涉及车辆各品种器材间的关系，反映了车辆装备保障部门的保障能力和车辆器材周转量确定的合理性[2]。

1.2 车辆器材需求量概率

目前，车辆周转器材基本为耗损类器材，多用于换件修理，为了保证本单位车辆器材不间断供应，通常将其储存在基层部队的仓库中。根据各基层单位车辆周转器材消耗的历史数据，可以认为该种车辆器材在某一供应周期内的需求量服从参数为λ的泊松分布，即任一品种车辆器材的需求量概率分布为

(2)

假设X1，X2，…，Xn为来自总体X的样本，则样本的似然函数为

(3)

则可得到λ的最大似然估算值为

(4)

从而可推导出车辆器材的需求量概率为

(5)

2 车辆器材保障度模型

2.1 传统保障度模型的不足

在解决车辆器材储备系统优化问题时，常依据可靠性理论和方法来建立保障度模型。常用的保障度模型有串联系统、并联系统、串—并联系统、并—串联系统[3]。现以可靠性数学模型中的串联系统为例，假设车辆器材周转量系统是一个由n个品种器材组成的串联系统，将串联系统的可靠度作为系统的保障度，依据BARLOW可靠性理论，则车辆器材周转量系统的最优分配问题保障度模型为

(6)

式中：Ri(mi)为各品种车辆器材的保障度；R0为车辆器材周转量系统保障度；mi为车辆器材周转量单品种数量；ci为各品种车辆器材的价格；Cm为车辆器材周转量经费总限额。

这种典型的保障度模型在部分结构比较简单的系统优化研究中能够取得比较理想的效果，但在车辆器材周转量系统的优化过程中却遇到了较大的困难。由于车辆器材周转量品种众多，如果仍以串联系统作为器材周转量单品种数量优化时的评价函数，即使每种器材的保障度都达到98%，那么20项器材的系统保障度也只有66．76%，更何况在实际工作中，单品种器材保障度很难达到98%，器材种类也远远大于20个，这就与部队车辆在实际使用中需具备较高可靠性的要求背道而驰。其他几个系统，则比较繁琐，且在实际应用中无法厘清各器材的串并联关系。为此，本文立足部队实际，改进传统保障度模型，建立了新的车辆器材周转量单品种数量优化模型。

2.2 改进的保障度模型

2.2.1 周转器材可靠度与储备数量的关系

由可靠度的概念可知，器材的可靠度就是器材储备(可靠度为100%)完全满足器材需求的置信度[4]。因此，对于单个车辆装备的某种器材而言，车辆器材的可靠度可表示为该种车辆器材的需求量小于等于车辆器材的储备数量的概率。通常按下式计算：

R=P(N(t)≤S)

(7)

式中：N(t)为车辆器材的需求量；S为车辆器材的储备数量；R为车辆器材的可靠度。

假设把时间间隔N(t)内某种车辆器材的需求量设为N(t)(0≤t≤T),则{N(t)，0≤t≤T}是一个泊松分布，时间连续，其值为非负整数。由式(5)可得，在整个供应周期内某种车辆器材i的需求量为Xi的概率为

(8)

根据概率论的相关公式可得该品种车辆器材的可靠度为

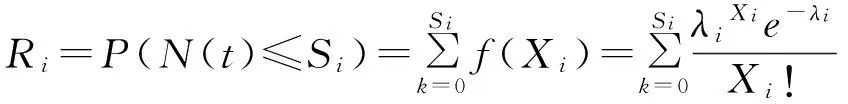
(9)

式中参数λi未知待求，如果参数λi已知，那么只需确定可靠度的值，即可求得该品种车辆器材需要储备的数量。反之，如若知道该品种车辆器材需要储备的数量 ，即可求出该品种车辆器材的可靠度。

2.2.2 车辆器材周转量系统保障度的确定

根据保障度的定义以及周转器材可靠度与车辆器材需要储备数量的关系，可构建车辆器材保障度模型[5]。

假设N为某种车型应储车辆周转器材种类数，由式(9)可得该车辆器材的可靠度为

(10)

由Ei的概念可知：

(11)

又因

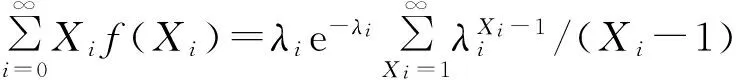
(12)

则

(13)

因此，车辆器材周转量系统保障度模型为

(14)

3 基于保障度的车辆器材周转量单品种数量优化模型

3.1 确定优化目标

车辆器材周转量单品种数量的优化目标是：在有限的经费条件约束下，尽可能地使车辆器材实际保障数量能够达到需求保障数量。根据建模需要，假设条件如下：

(1)一个供应周期内只供应保障一次器材；

(2)车辆器材价格在整个供应周期内保持不变；

(3)按照车辆器材重要度的等级划分进行器材控制。

3.2 车辆器材周转量单品种数量优化模型

以模型的假设条件为基础，建立目标规划模型对车辆器材周转量单品种数量进行优化[6]。具体模型如下：

目标函数为

(15)

约束条件为

(16)

其中

式中：L为车辆器材周转量系统保障度；Lv为重要器材的保障度；Le为较重要器材的保障度；Ld为一般重要器材的保障度；A为车辆器材周转量系统保障度目标值；V为重要器材的保障度目标值；E为较重要器材的保障度目标值；D为一般重要器材的保障度目标值；n为车辆器材周转量的总品种数；kv为重要器材的品种数；ke为较重要器材的品种数；kd为一般重要器材的品种数；Ci为车辆器材单价；Cs为所储车辆器材的总费用；C为车辆器材保障经费总限额。

3.3 模型优化算法

上述模型用于解决结构相对简单的车辆器材储备数量优化问题时，可采用爬山法、动态规划法、单纯形法或遗传算法等直接进行求解。但是由于车辆器材种类繁多、构造复杂，如果采用传统方法对所有的车辆周转器材进行求解，其计算过程将非常复杂，甚至难以求出最优解。因此，当考虑到所有车辆周转器材时，采用粒子群算法进行优化较为有效。

4 实例验证

4.1 车辆器材周转量单品种数量优化

以SX2190型牵引车为例。SX2190型牵引车为多数部队的主要装备车型，年行驶总程在5 000 km左右，由于对SX2190型牵引车的车辆器材历史消耗数据作了较为详细的记录，从而保证了数据的准确性、可靠性和完整性，因此，本文选取SX2190型牵引车的113种车辆器材作为研究对象，对车辆器材周转量单品种数量进行优化。

为了降低计算方法的复杂性，提高优化模型的可行性和方便性，本文利用Matlab软件设计了车辆器材周转量单品种数量计算程序(如图1所示)[7]。

根据深入基层部队、仓库实际调研所统计的历史数据和长期从事车辆器材保障工作的经验总结，将该车型车辆器材周转量系统的保障度目标值定为90%，重要器材、较重要器材、一般重要器材的保障度目标值分别定为95%、90%和85%。通过该计算程序可以求得满足保障度要求的车辆器材周转量单品种数量和系统的最优费用。部分具体运算结果见表1。

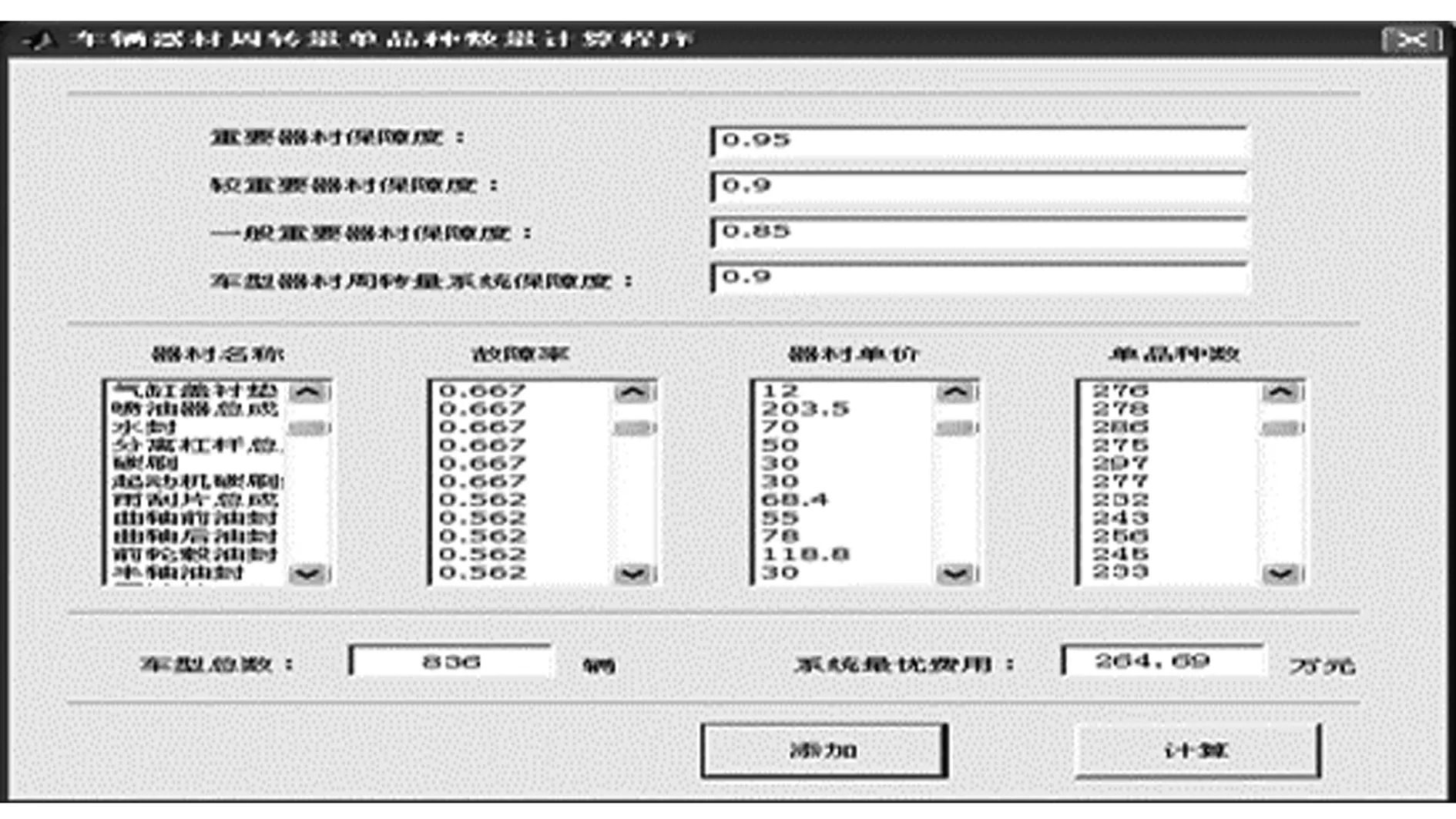
图1 车辆器材周转量单品种数量计算程序

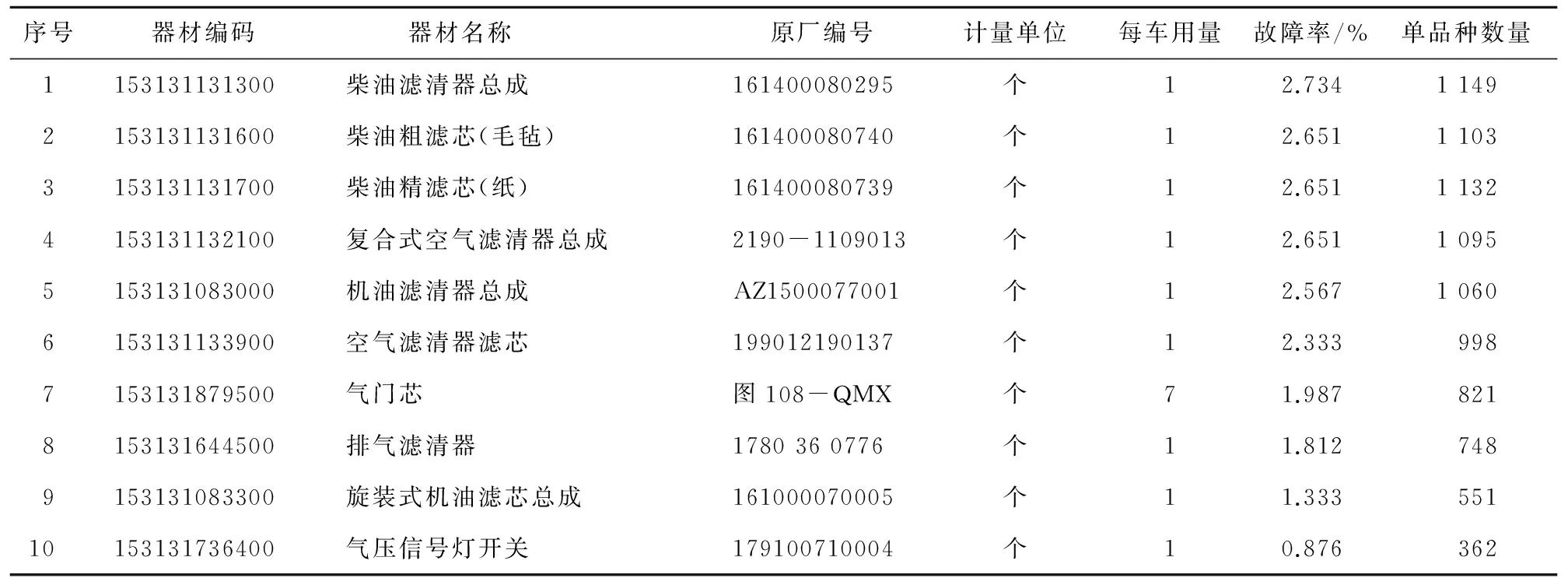
表1 部分器材周转量单品种数量优化结果统计

通过上述计算程序可得SX2190车型的车辆器材周转量的保障度R=90．13%>90%(满足车辆器材周转系统保障度大于90%的约束条件),该车型的最优费用为264．69万元。考虑到我军部队数量较多，地理分布较广，环境状况不尽相同，同一车辆器材在不同地区、不同单位的消耗情况也有所差异，因此，通过模型求解得到的车辆器材周转量单品种数量只能作为参考，在对具体单位、具体车型进行分析时，还应根据部队实际情况加以修正。

4.2 结果分析

依循上述方法，可以对其他车辆器材周转量进行优化。但理论与实际总有或多或少的差距，根据上述方法确定的车辆器材周转量品种、单品种数量是否满足实际要求，满足程度达到多少，能否直接作为车辆周转器材储备建立的依据，还需要对优化结果进行分析。

4.2.1 品种覆盖率分析

品种覆盖率即车辆器材周转量品种占应储器材品种的百分比。车辆器材周转量的优化以经费限额为绝对约束条件，这可能导致部分车型由于经费不足而造成部分器材未能储备。一般而言，同一车型，部队装备配备数量越大，该车型器材周转量的品种覆盖率越高，部队配备数量越少，品种覆盖率越低[8]。其主要原因是装备配备数量少的部队供应周期内器材消耗量少(大多器材年消耗不足1件)，而进行周转量优化时，各器材周转量的单品种数量为整数且重要类器材优先保障，从而造成部分器材的保障度过高，占用了大量的经费，造成器材储备品种的减少。因此，对某具体车型而言，品种覆盖率的检验一般从配备该车型数量最少的部队开始，如果该部队能够满足要求，即可认为该车型的品种覆盖率符合要求。根据调研数据，选取6种车型进行器材周转量品种优化，将优化结果与部队收集的数据进行对比，最终得出各车型最低器材周转量品种覆盖率，具体结果见表2。

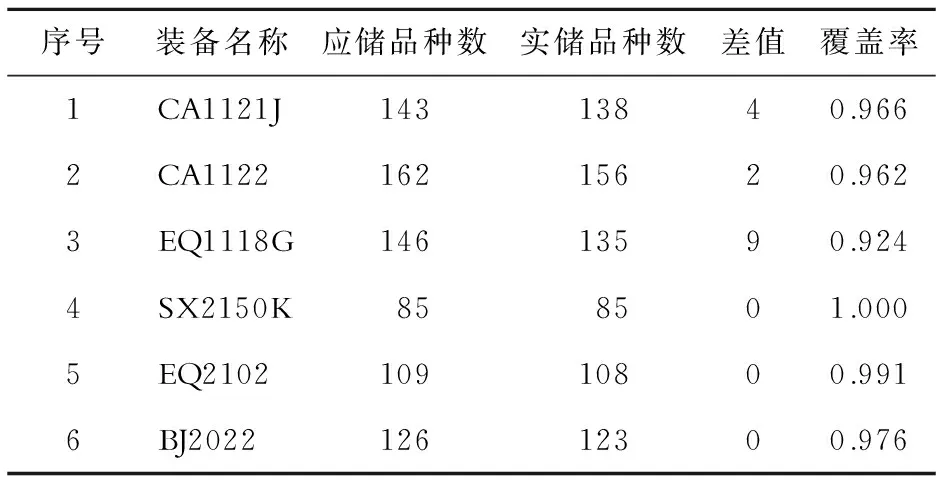
表2 各车型最低器材周转量品种覆盖率统计

4.2.2 器材周转量单品种数量检验

器材周转量单品种数量的检验可由器材可靠度的高低来体现，由于优化模型的约束条件对各类器材的保障度作了限制，而保障度与可靠度密切相关，这保证了优化结果中各品种器材的可靠度处于较高水平，因此，可以认为优化结果所确定的车辆器材周转量单品种数量是合理的。

5 结 语

以车辆器材保障度的概念为基础，厘清了车辆器材需求量与车辆器材保障度之间的关系，给出了可靠性数学模型，并以串联系统为例，建立了传统的保障度模型，分析了传统保障度模型的不足，并加以优化改进，建立了基于保障度的车辆器材周转量单品种数量优化模型，并采用较为先进的粒子群优化算法对数学模型进行求解，使模型求解的结果更加接近部队车辆周转器材储备实际情况。

[1] 潘建．航材库存系统优化与实现[D]．天津：中国民用航空学院，2006：20-27．

[2] 王亮,尹永超,田朝友.基于保障度的车辆器材周转量优化研究[J].物流技术，2013，32(12)：436-441.

[3] 余高达，赵潞生．军事装备学[M]．北京：国防大学出版社，2000：468-475．

[4] 王亮．军用车辆装备器材保障[M]．天津：军事交通学院，2002：58-68．

[5] 赵复涛.军用车辆器材周转量[D].天津：军事交通学院，2012:21-29．

[6] 周林，王君．军事装备管理预测与决策[M]．北京：国防工业出版社，2007：10．

[7] 袁慧华.群算法的城市绿波优化设计[J].甘肃科技，2010，26(24)：74-76.

[8] 龙绵伟．美军后勤装备体制机制研究[J]．军事交通学院学报， 2011，13(12)：82-86．

(编辑：关立哲)

Single-type Vehicle Material Turnover Volume Optimization Based on Supportability

WANG Liang1, WEN Zhengzhong2, HE Jian2, LYU Zhiming3

(1． Military Vehicle Department, Military Transportation University, Tianjin 300161, China；2． Postgraduate Training Brigade, Military Transportation Unviersity, Tianjin 300161, China;3. Logisitics Equipment Maintenance Training Center, Ji’nan Military Region, Ji’nan 250022, China)

To properly solve the problem of single-type vehicle material turnover volume optimization, the paper establishes optimization model based on supportability according to supportability theory, and solves the model with particle swarm optimization (PSO) and verifies the result through real case. The study shows that designing vehicle material turnover volume optimization system with programming language increased the practicability and operability of the optimization model, and the analysis of the result verified the reasonability of the model.

vehicle material; turnover volume; supportability; optimization model; particle swarm optimization

2015-08-31；

2015-10-09． 作者简介： 王 亮(1962—)，男，教授，硕士研究生导师．

10．16807/j.cnki.12-1372/e.2016.03.006

E234

A

1674-2192(2016)03- 0023- 05