机场应急投送能力评估模型的构建

夏军剑，夏爱生，刘俊峰，张新巍

(军事交通学院 基础部，天津 300161)



● 基础科学与技术 Basic Science & Technology

机场应急投送能力评估模型的构建

夏军剑，夏爱生，刘俊峰，张新巍

(军事交通学院 基础部，天津 300161)

针对机场应急投送能力评估问题，采用多类顾客闭合排队网络建立性能评价模型，对平均值分析算法提出具体处理方法，使之适应多类飞机型号、多种运输任务的需求，并运用模型进行了理论计算。通过将计算结果与蒙特卡洛仿真结果对比分析表明，建立的模型反映了真实系统的性能变化趋势；通过模型分析，可以发现系统的瓶颈资源，预测系统某个服务中心服务台数量的变化对整个系统的影响程度。

投送能力评估；MVA算法；闭排队网络；蒙特卡洛仿真；出动架次率

航空运输是战略投送的主要手段，加强航空运输能力是战略投送能力建设的重要部分。机场是航空运输系统中的重要基础设施，是连接航空运输和其他运输方式的桥梁和纽带，是运输网络的重要节点。随着航空运量的快速增长，对机场的运输能力也提出了更高的要求。机场设施建设需要占用大量资金，因而对整个空运系统进行分析和优化，有助于机场进行科学管理，优化设施配置，降低建设成本，改善运输质量，提高运输效率，避免资源浪费。

对于航空运输能力，架次率是衡量其能力的一个重要指标[1]。常用的出动架次率的计算方法有类比法、解析法和仿真法。仿真法能精确分析，国内外研究成果比较多[2-4]，但仿真模型适应性差，建模复杂，计算耗时。孙蛟等[5]提出了基于时间分割思想的工程计算方法，建立了出动架次率计算模型，但只计算了单架飞机的时间指标。飞机从机场起飞至回到机场，可以认为是一个封闭的系统，出动回收的流程中任一环节都可看成顾客到达服务然后离开的过程，可以运用闭排队网络的成熟理论进行建模与分析。通常利用均值(如平均服务时间、平均到达速率)来参数化排队模型，利用均值分析法(mean value analysis，MVA)求解[6]。Dietz等[7]提出将Fork-Join闭排队网络的MVA法应用于飞机架次率的建模分析上，获得了飞机出动架次率的解析结果。夏国清等[8]提出一种共享服务器的MVA法，并用于飞机出动能力的研究中。本文提出将多种顾客源的时间参数均值化的方法，结合闭排队网络模型，得到整个系统的性能参数，用于分析机场的应急投送能力，最后通过仿真模型进行对比和验证。

1 机场应急空中输送系统分析

机场应急投送系统是战略投送系统重要的子系统，其作业流程可分为5部分：飞行前准备、飞行与飞行后检查、预防性维修、修复性维修、物资装备装卸载(人员登离机)和加油。其中，在充分利用飞机的装载能力的情况下，某型号的飞机装卸时间和加油时间几乎是固定的。

整个应急投送系统作业流程如图1所示。整个过程可以将运输机看作客户，各种活动为运输机接受的服务，基本符合闭排队网络的条件，即客户只在网络内部转移，且没有外部客户到达，可以建立机场应急投送系统的闭排队网络模型。

图1 机场应急投送系统作业流程

为了表达方便，定义飞行前准备、飞行、预防性维修、修复性维修、装卸载(加油)分别用节点1—5表示。由于运输机型号不同、服役时间不同、运输任务不同，因此整个机场应急投送系统可以认为具有K类顾客，每类顾客具有Nk(k= 1,2,…,K)个客户，有M个服务中心的闭排队网络模型。第k(k= 1,2,…,K)类顾客的每架运输机在第i服务中心完成服务后，以一定概率pkij转移到服务中心j，可以用矩阵Pk(k= 1,2,…,K)描述。在整个系统中，架次率可用单位内“飞行位”的吞吐量表示。飞机在各服务中心转移并接受服务，本文假定各服务中心服务时间都服从负指数分布。服务中心服务器的数量为同时接受服务的飞机数量，反映各节点的服务能力。

2 机场应急空中输送系统保障能力计算方法

对于闭排队网络求解的常规方法是平均值分析方法[9]。本文的顾客种类呈现多样化，因此，服务节点的服务时间不能用同一分布表示。本文提出对服务时间平均值的计算方法进行近似处理而得到近似平均值分析法来求解闭排队网络模型。

2.1 状态转移矩阵和服务时间平均值计算方法

对任意服务中心i*，第k类顾客平均每到达服务中心i*一次，相应到达服务中心i的次数满足方程[6]：

(1)

式中：Pk为第k(k= 1,2,…,K)类顾客的状态转移矩阵；vk为一向量。

为计算第k类顾客执行一次飞行任务的平均周转时间，设定i*=2，令vk2=1，则得到飞机在服务中心i的吞吐量与“飞行”状态吞吐量之比vk=[vk1，vk2,…，vkM]。

于是，第k类顾客执行一次飞行任务平均周转周期为

(2)

式中tki为第k类顾客在节点i的平均服务时间。

第k类顾客飞行架次率rk为

(3)

第k类顾客在第i个服务中心占有比例ηki为

(4)

第i个服务中心等效平均服务时间ti为

(5)

系统内的顾客数量N为

(6)

k类顾客平均的等效状态转移矩阵的项为

(7)

通过以上处理方法，我们最终得到一个有N个顾客、M个服务中心、状态转移矩阵为P=[pij]、第i个服务中心服务时间为ti的闭排队网络模型。

2.2 MVA算法

到达定理(arrival theorem)是MVA算法的理论基础。它证明了在一个封闭的网络中，如果有N个客户，一个刚到达节点的客户看到的到达此节点的客户数量的分布，为该系统中少一个客户(N-1)时的此节点的客户数量的分布。由到达定理可得

μi(n)Pi(n|N)=λi(N)Pi(n-1|N-1)

(8)

式中：Pi(n|N)为在网络中有N个客户的情况下，第i个服务台有n个客户的概率；λi(N)为在网络中有N个客户时，客户到达第i个服务台的速度(由于稳定状态下客户到达的速度等于离去的速度，所以也可以称λi(N)为吞吐量)；μi(N)为第i个服务台有n个客户时的服务速度：

(9)

式中ti为第i个服务中心的服务时间。

客户在第i个服务中心的停留时间为

(10)

根据式(3)可以得到，客户在整个网络中的循环周期是客户两次经过同一个服务中心的平均时间。显然，不同的服务中心对应循环周期是不一定相同的。为便于讨论，将循环周期定义为客户两次到达服务中心2的平均时间间隔：

(11)

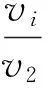
令V=(v1，v2，…,vM)，设v2=1，则V=VP，因为路径转移矩阵P是不可约的，所以V有唯一解。

根据客户在闭排队网络的循环周期，可以计算网络中有N个客户时各个服务中心吞吐量：

(12)

根据Little定理可得，第i个服务中心总的客户数量Qi(N)和正在接受服务的客户数量Qs,i(N)为

Qi(N)=Ri(N)λi(N)

(13)

Qs,i(N)=tiλi(N)

(14)

第i个服务中心的服务器利用率即为正在接受服务的客户数量与服务器数量比值：

Ui(N)=Qs,i(N)/ri

(15)

对式(8)稍加变动即可得到式(16)，从而可以计算出客户分布Pi(n|N)：

Pi(n|N)=λi(N)Pi(n-1|N-1)/μi(n)

(16)

(17)

以上方程揭示了排队网络中有N个客户和N-1个客户时的概率分布关系。若知N-1个客户时的概率分布，就可以推算出有N个客户时的概率分布。对于任何排队网络都有N=1时，Pi(0|N-1)=1和Qi(N-1)=0，由此经过迭代运算，可求得闭排队网络中有任意客户时的分布。

2.3 多类顾客分布情况和吞吐量计算

由公式(4)、(13)，可以得到第k类顾客在第i个服务中心总客户数量Qki(N)：

Qki(N)=Qi(N)ηki

(18)

由公式(4)、(12)，可以得到第k类顾客在第i个服务中心总吞吐量λki(N)：

λki(N)=λi(N)ηki

(19)

3 实例分析

以3种类型的飞机执行多种运输任务为例，划分顾客种类，给出了各服务中心的平均服务时间、已配置的服务台数目。假定服务时间都服从负指数分布(见表1)。飞机到达飞行前准备和飞行两个服务中心不需要等待，能立刻被处理，所以服务器的数目设为无穷。其他服务中心都配备了有限数目的服务器。

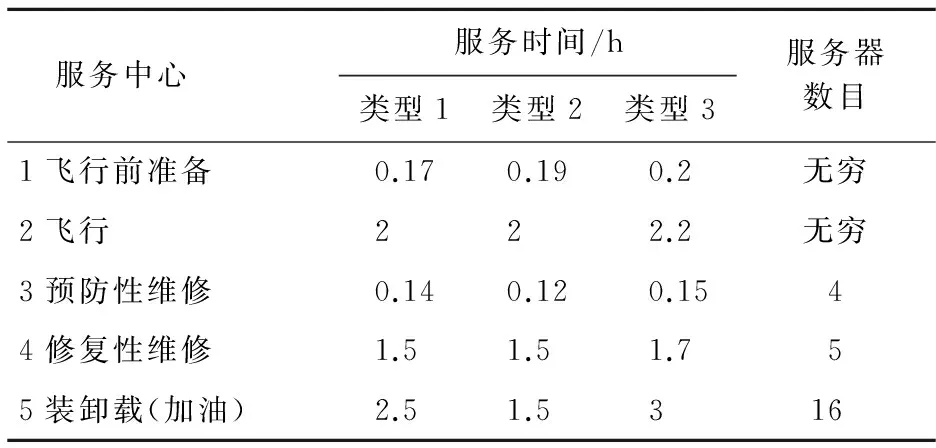
表1 出动回收过程相关参数

3类飞机的状态转移概率矩阵为

由公式(1)—(7)计算可得平均周转时间：T1=5．176 1 h、T2=4．187 9 h、T3=5．973 3 h。

飞机数量N=50，各服务中心平均服务时间和顾客在服务中心占有比率见表2。

由表2可以看出，虽然总的飞机数相同，但不同类型的顾客有不同的周转时间，所以周转时间长的实际占有比例要偏小，周转时间短的实际占有比例偏大。

表2 顾客在各服务中心比率计算结果

对于平均状态转移概率矩阵，当N1=15、N2=10、N3=25时：

当N1=15、N2=25、N3=10时：

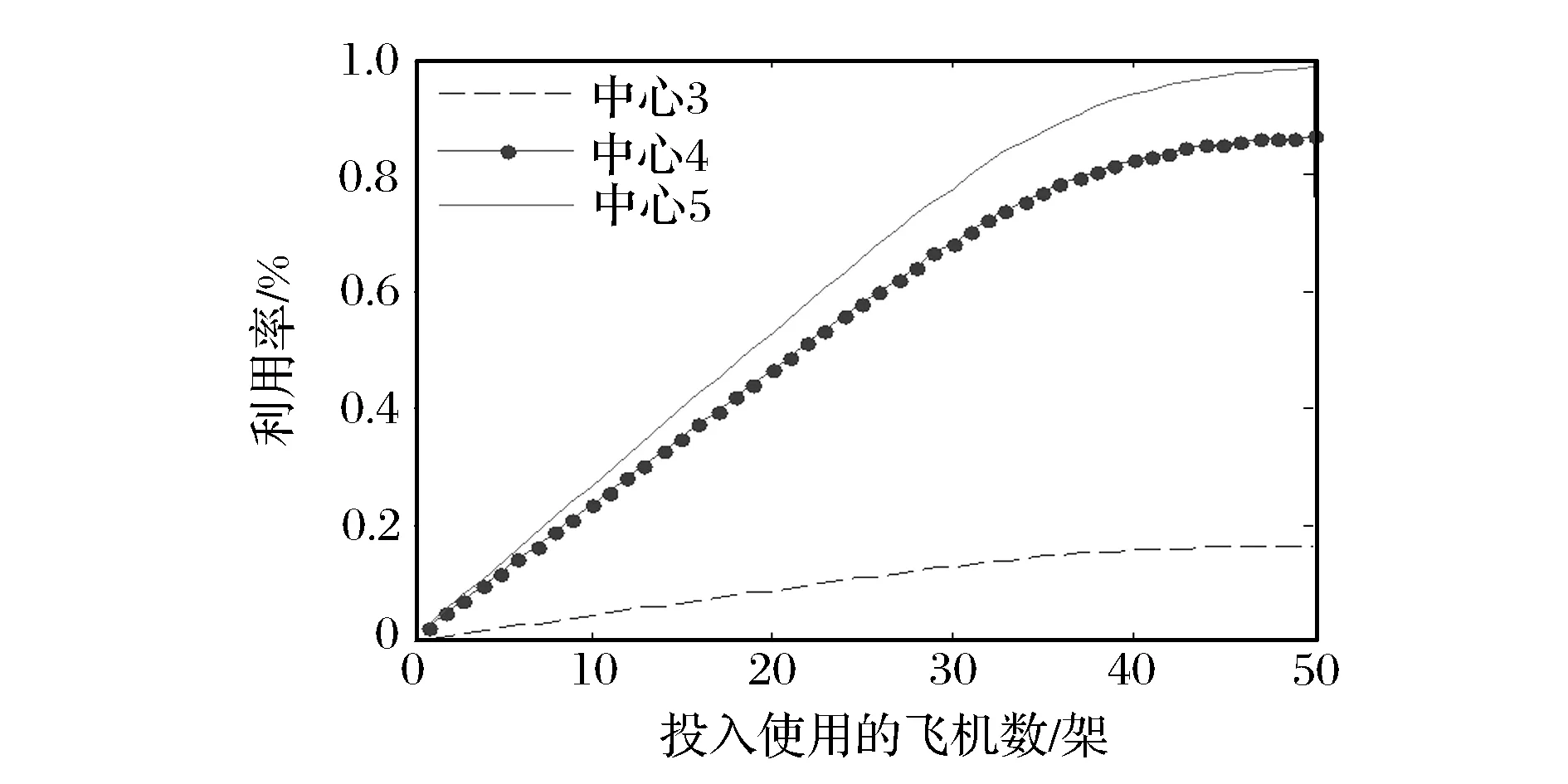
使用MVA算法后得到架次率如图2所示，虽然飞机总数一致，但由于类型比重不同，所以总体的架次率是不一致的。当三者比重为15∶10∶25时，N<30时呈线性上升趋势，N>40时，趋势平缓；当三者比重为15∶25∶10时，N<35时呈线性上升趋势，N>45时，趋势平缓。说明不同类型的顾客对资源的需求是不一样的，周转时间短的顾客占用资源少，可以得到更多的出动架次率，周转时间长的顾客占用资源多，出动架次要少。不管是哪一种比率，当架次率增加趋于平缓时，单纯增加飞机数量已经不能提高飞机的出动能力。服务中心利用率如图3所示，可以看出飞机出动的瓶颈在装卸载(加油)环节，随着飞机数量的增加，装卸载(加油)环节首先达到100%，所以制约架次率的关键因素是装卸载(加油)环节。

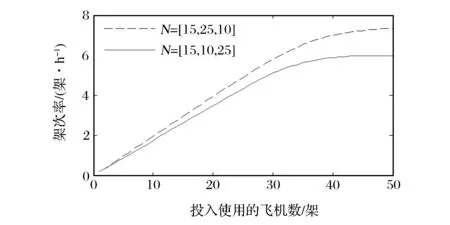
(a)3种类型飞机

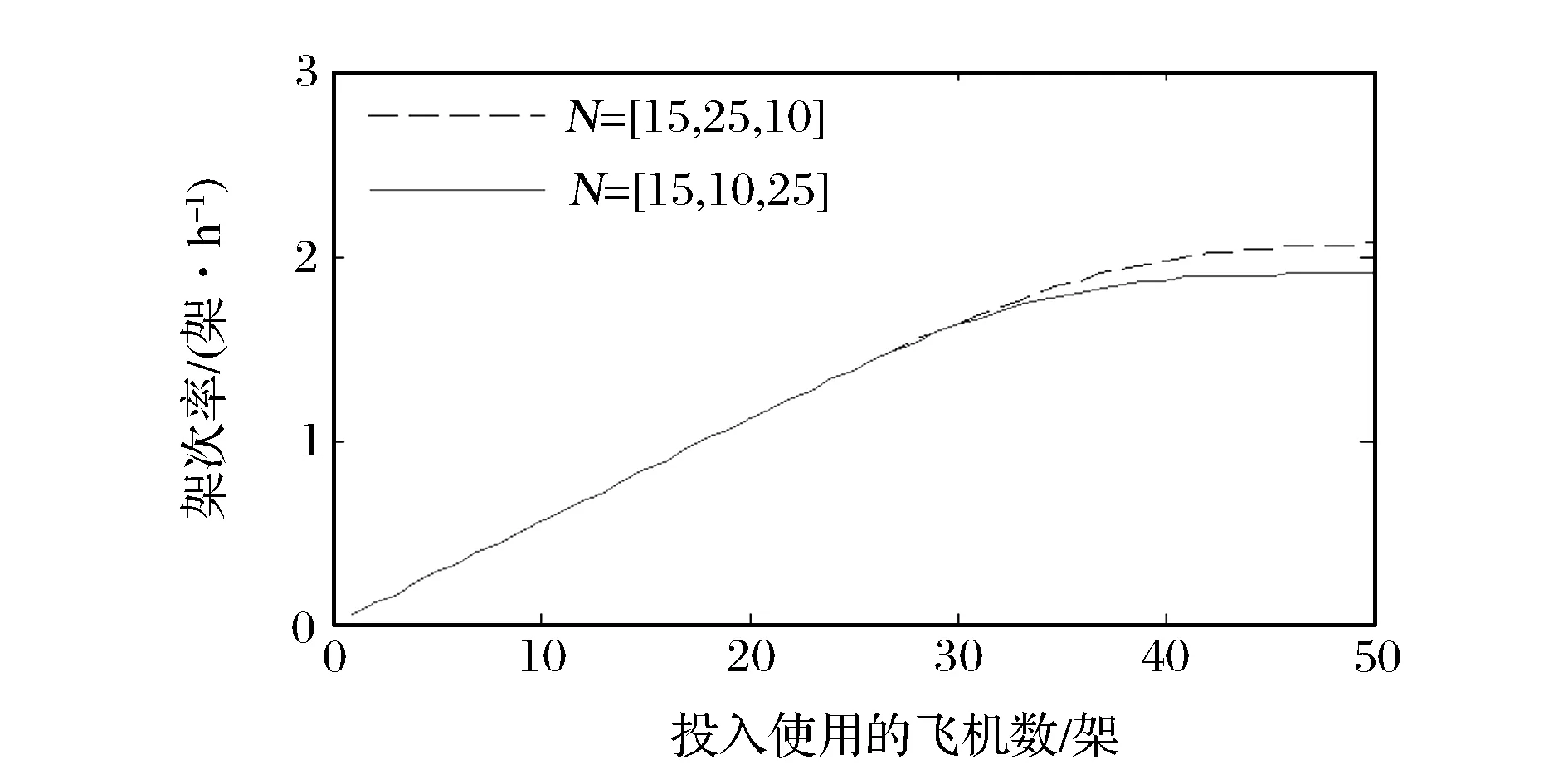
(b)类型1飞机

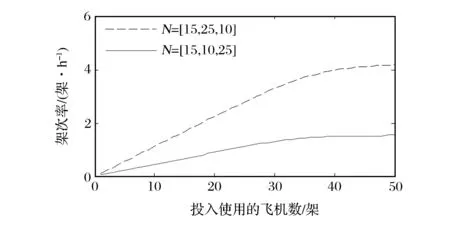
(c)类型2飞机

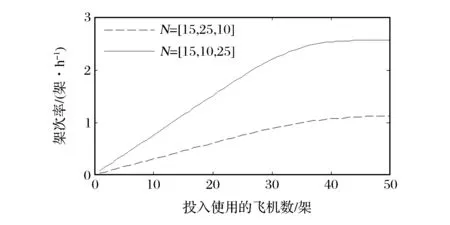
(d)类型3飞机

(a)N=[15，25，10]时

(b)N=[15，10，25]时

由公式(18)、(19)可求出各种类型顾客实际的吞吐量和在各服务中心的顾客数(见表3、4)。

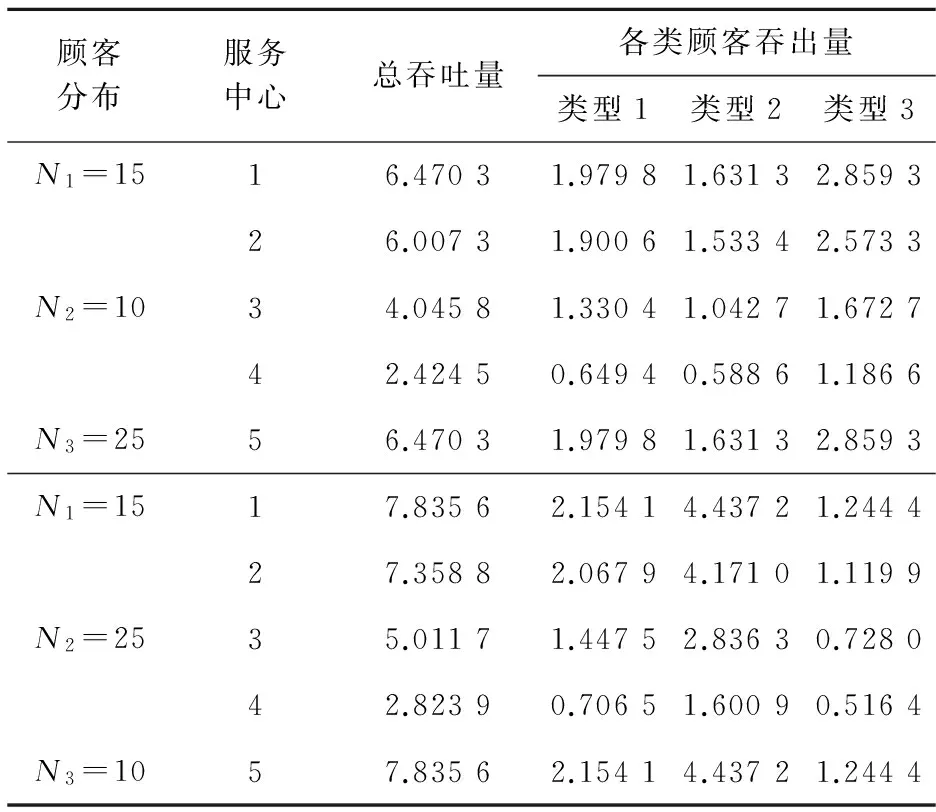
表3 吞吐量数据

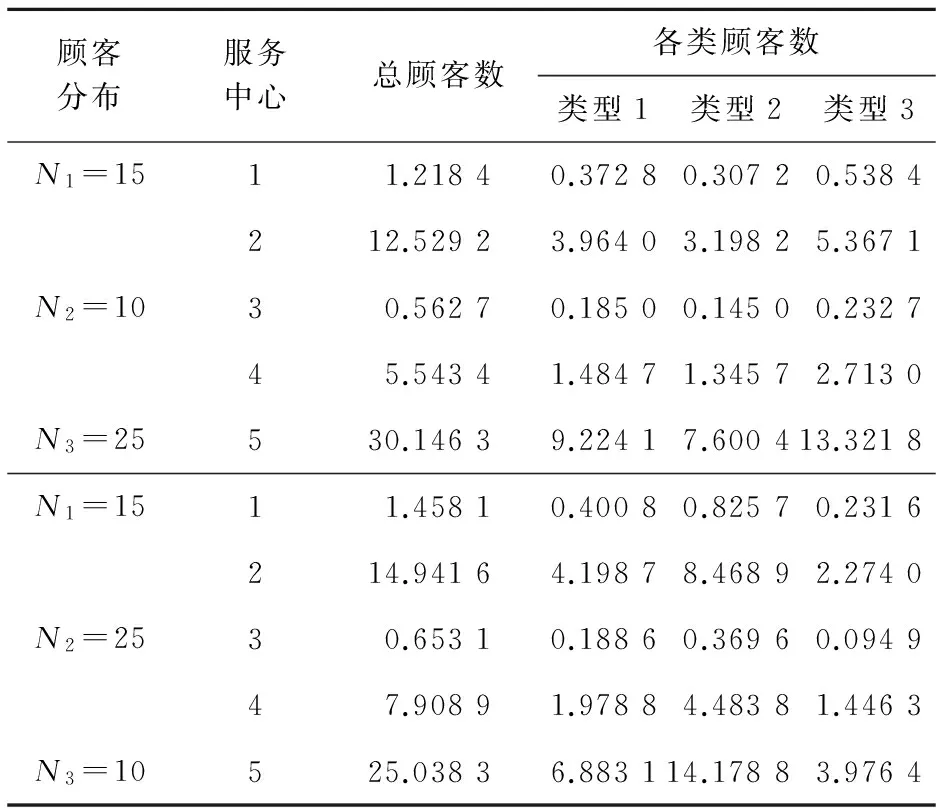
表4 各服务中心顾客数

为了对所建模型的性能指标进行验证，基于模特卡罗方法建立了多顾客闭排队网络系统的仿真模型，仿真时间5×103h，按N= 30、N= 50两种情况为例进行模拟。表5为本文建立的解析方法和仿真结果的对比数据，从表5各服务中心吞吐量和利用率的数据可以看出本文的解析模型能正确地对机场的性能进行评价。

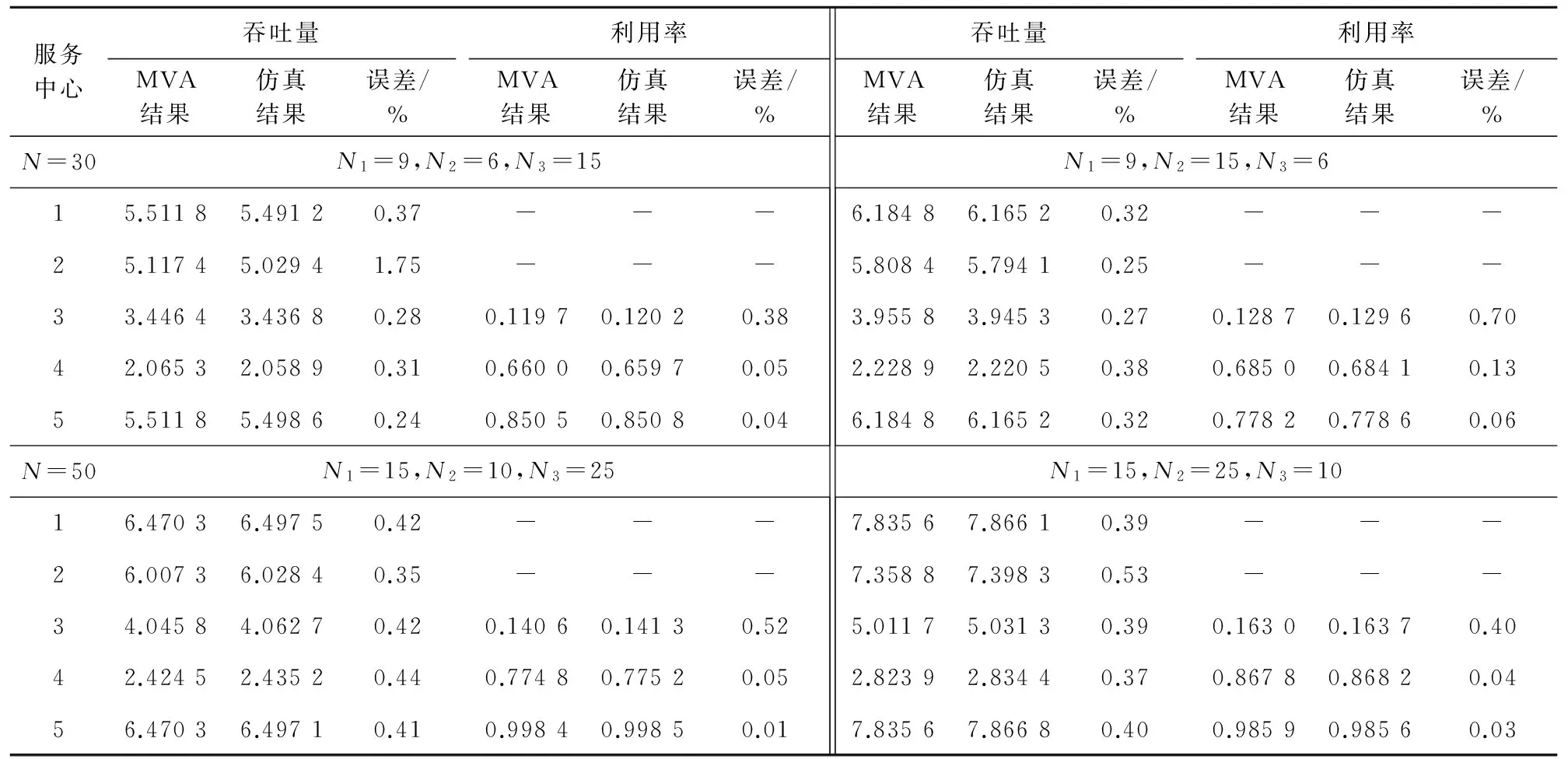
表5 MVA算法和仿真的服务中心吞吐量和利用率对比结果

4 结 语

对于机场应急投送能力问题，基于闭排队理论建立解析模型。该模型充分考虑了不同类型飞机执行不同运输任务的情况，对所给参数进行了平均值处理，利用MVA算法求出飞机出动架次率，为应急投送提供参考。通过模型的结果与仿真结果的对比，说明所建解析模型是合理的，可以在投送任务开始前有效地对机场的实际投送能力进行评价，实现对人员、物资、装备的合理调配，为决策者制订决策方案提供理论支持。

[1] 国防科工委综合计划部．装备综合保障通用要求:GJB 1999—3872[S].北京:国防科工委军用标准化中心,1999:15.

[2] HARRIS J W. The Sortie Generation Rate Model[C]//Proceedings of the 2002 Winter Simulation Conference, 2002:864-868.

[3] PATTINGGILL K B.An analysis of the efficacy of the logistics composite model in estimating maintenance manpower productive capacity[D].Dayton: American Air Force Institute of Technology,2003:13-45.

[4] 方绍强,卫克,陈伟鹏.基于ARENA的战场飞行保障过程建模与仿真[J].系统仿真学报,2008, 20(3):746-750.

[5] 孙蛟,赵彬,辛文逵.军用飞机出动架次率工程计算方法[J].空军装备研究,2009,3(6):30-33.

[6] REISER M,LAVENBERG S S.Mean-value analysis of closed Multichain queueing networks[J].Journal of the ACM,1980,27(2):313-322.

[7] DIETZ D C,JERKINS R C.Analysis of aircraft sortie with the use of a fork-join queueing network mode[J].Naval Logistics Research,1997,2(44):153-164.

[8] 夏国清,陈红召,王元慧.基于闭排队网络的飞机出动架次率分析[J].系统工程学报,2011,26(5): 686-693.

[9] GUO L W, AU O C, MA M Y, et al. A novel analytic quantization-distortion model for hybrid video coding [J].IEEE Transcations on Circuits and Systems for Video Technology,2009,19(5):627-641.

(编辑：张峰)

Construction of Airport Emergency Projection Ability Evaluation Model

XIA Junjian, XIA Aisheng, LIU Junfeng, ZHANG Xinwei

(General Courses Department, Military Transportation University, Tianjin 300161, China)

Considering the problem of airport emergency projection ability evaluation, the paper constructs a performance evaluation model with multi-customer closed queuing network (MCQN) and proposes specific method to treat mean value analysis (MVA) adapting to various planes and many kinds of transportation tasks, and makes theoretical calculation with this model. The comparative analysis of the calculation result and Monte Carlo simulation shows that the model reflects the performance trend of the real system, and we can find the bottleneck resource of the system and predict the influence degree of service desks’ quantity change on overall system through model analysis.

projection ability evaluation; MVA algorithm; closed queuing network; Monte Carlo simulation; sortie generation rate

2015-09-15；

2015-10-22． 作者简介： 夏军剑(1978—)，男，硕士，讲师．

10．16807/j.cnki.12-1372/e.2016.03.017

V352

A

1674-2192(2016)03- 0075- 06