锐角三角函数学习导引

2016-12-22

初中生世界 2016年47期

关键词：坡角锐角三角锐角

锐角三角函数学习导引

崔恒刘

本章的重点是锐角三角函数的定义和直角三角形的解法，难点是综合运用知识解决实际问题.通过本章的学习，同学们要会使用计算器由已知锐角求它的三角函数值，由已知三角函数值求相应锐角，能运用锐角三角函数解直角三角形及相关的实际问题.

一、深入理解锐角三角函数的概念

1.理解锐角三角函数的定义.

（1）正切、正弦和余弦的概念是在一个直角三角形中定义的，其本质是两条线段的比值，没有单位，其大小只与角的大小有关，与其所在的直角三角形的大小无关；

（3）正切tanA、正弦sinA和余弦cosA是一个完整的符号，tanA不是tan与A的积，离开了∠A，“tan”就没有意义了，只有合起来，tanA才表示∠A的正切，sinA、cosA也是如此；

（4）符号tanA表示∠A的正切，在符号tanA中，习惯省去角的符号“∠”，当用希腊字母α、β等表示角时，其正切中角的符号习惯上也省去，但当用三个英文字母或阿拉伯数字表示角时，角的符号“∠”不能省略，sinA、cosA也是如此，如tanα、sin∠ABC、cos∠1等.

2.应用锐角三角函数的定义.

例1（2016·甘肃兰州）在Rt△ABC中，∠C=90°，sinA=，BC=6，则AB=（）.

A.4 B.6 C.8 D.10

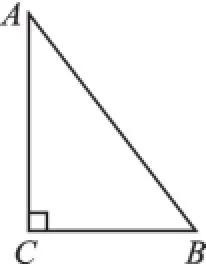
图1

【分析】先画出图形，如图1，在Rt△ABC中，由锐角三角函数定义表示出sinA，将sinA的值与BC的长代入即可求出AB的长.

【评注】熟练掌握锐角三角函数的基本概念是解好本题的关键，做题时边读题边画一个直角三角形，数形结合、看图说话，可避免主观出错.

二、理解记忆特殊角的三角函数值

任意角的三角函数值都可以由计算器获取，但由于特殊角的三角函数值常见常用，所以应当记忆，这样便于我们运用它们进行计算、求值和解直角三角形.

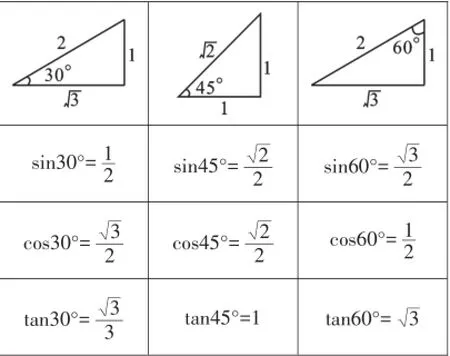
另外，观察表格，我们还有收获.横着看：正弦值、正切值，随着角度的增大而增大（其中tan30°·tan60°=1=tan45°）；余弦值，随着角度的增大而减小.这个规律是不是一般规律？对所有的锐角三角函数都成立吗？有兴趣的同学可借助于计算器验证一下自己的发现.竖着看：sin45°=cos45°；斜着看：sin30°=cos60°，sin60°=cos30°.学习数学，要善于观察、思考，这样才能不断提升自己.

例2式子的值是（）.

A.2?3-2 B.0 C.2?3 D.2

【分析】将特殊角的三角函数值代入后，化简即可得出答案.原式=2×

【评注】本题考查了特殊角的三角函数值，因此，一些特殊角的三角函数值需要我们在理解的基础上熟练记忆.

例3已知tanA=，∠A为锐角，则∠A的取值范围是（）.

A.0°＜∠A＜30° B.30°＜∠A＜45°

C.45°＜∠A＜60° D.60°＜∠A＜90°

【分析】要确定∠A的取值范围，只要确定在哪两个特殊角的三角函数值之间即可.因为所以tan30°＜tanA＜tan45°，所以30°＜∠A＜45°，故选B.

【评注】解答本题不仅要熟记特殊角的三角函数值，还要理解“锐角三角函数的正切值随着角度的增大而增大”这个规律.

三、解直角三角形及其应用

1.直角三角形各元素之间的关系.

如图2，在Rt△ABC中，∠C=90°，a、b、c分别是∠A的对边、∠B的对边和∠C的对边.除直角外的五个元素之间有如下的关系：

三边之间的关系：a2+b2=c2；

两个锐角之间的关系：∠A+∠B=90°；

图2

2.解直角三角形的基本类型及解法.

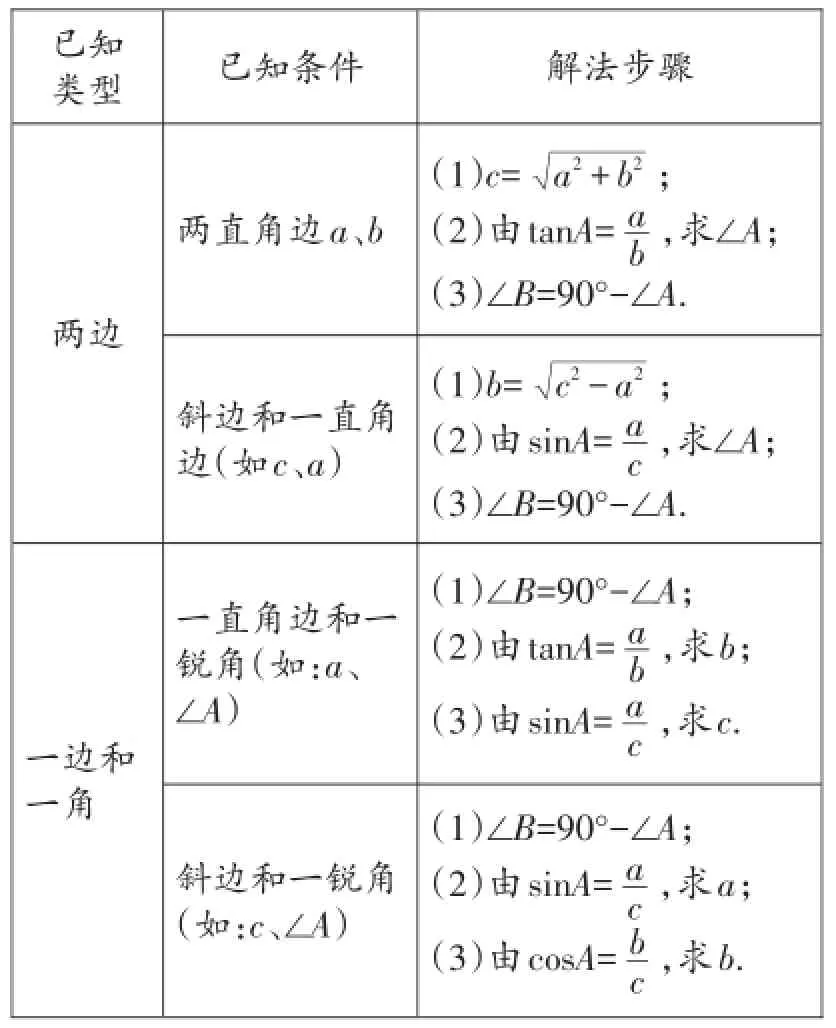
已知类型已知条件解法步骤（1）c =两直角边a、b a2+ b2；（2）由t a n A =两边ab，求∠A；（3）∠B = 9 0 ° -∠A .（1）b = c2-a2；（2）由s i n A =斜边和一直角边（如c、a）ac，求∠A；（3）∠B = 9 0 ° -∠A .（1）∠B = 9 0 ° -∠A；（2）由t a n A = ab，求b；（3）由s i n A =一直角边和一锐角（如：a、∠A）一边和一角ac，求c .斜边和一锐角（如：c、∠A）（1）∠B = 9 0 ° -∠A；（2）由s i n A = ac，求a；（3）由c o s A = bc，求b .

由此我们知道：在直角三角形的六个元素中，除直角外的五个元素，只要知道两个元素（其中至少有一个是边），就可以求出其余的三个元素.解直角三角形的知识广泛应用于生活，尤其在测量过程中用于计算距离、高度、长度和角度等.

例4（2016·江苏苏州）如图3，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为（）.

虽然文章开头可千变万化，但作为初中学生来讲，还是要靠船下篙，简洁明了为好，课文中此类开头也很多，这里不再一一列举。我们老师在实际教学中，要根据学生的实际情况，灵活地运用文章开头的方法。

C（.2?3-2）m D（.2?6-2）m

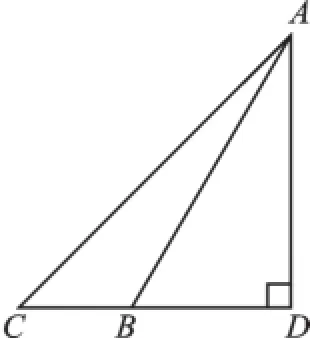
图3

【分析】先在Rt△ABD中利用正弦的定义计算出AD，然后在Rt△ACD中利用正弦的定义计算AC即可.

【解答】在Rt△ABD中，sin∠ABD=

【点评】解直角三角形的关键是抓住已知条件，利用已知的边和角求出未知的边，进而解决问题.

例5（2016·四川巴中）一个公共房门前的台阶高出地面1.2米，台阶拆除后，换成供轮椅行走的斜坡，数据如图4所示，则下列关系或说法正确的是（）.

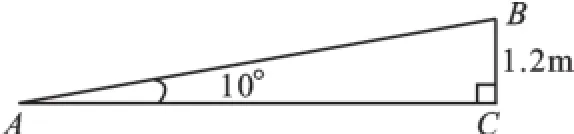
图4

A.斜坡AB的坡度是10°

C.AC=1.2tan10°米

【分析】坡度反映了斜坡的陡峭程度（这个度的意义不是角度），它是坡面的铅直高度h和水平宽度l的比，又叫做坡比，是一个比值，一般用i表示，常写成i=h∶l的形式.把坡面与水平面的夹角α叫做坡角，坡度i与坡角α之间的关系为：i=tanα.

【解答】根据坡度是坡角的正切值得斜坡AB的坡度是i==tan10°，选：B.

【点评】本题考查了解直角三角形应用中的基本概念：坡度、坡角，理解坡度的含义是解题的关键.

例5（2016·山东菏泽）南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，如图5，当渔船航行至B处时，测得该岛位于正北方向20（1+3）海里的C处，为了防止某国巡警干扰，就请求我国A处的渔监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离.