弹性支承圆弧钢浅拱弹塑性极限承载力分析
2016-12-22卢鹏,李涛,芦燕,3
卢 鹏, 李 涛, 芦 燕,3
(1.天津大学 建筑工程学院,天津 300072; 2.山东同圆设计集团有限公司,山东 济南 250000;3.天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300072)
弹性支承圆弧钢浅拱弹塑性极限承载力分析
卢 鹏1, 李 涛2, 芦 燕1,3
(1.天津大学 建筑工程学院,天津 300072; 2.山东同圆设计集团有限公司,山东 济南 250000;3.天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300072)
实际工程中许多拱结构支承于其他结构之上,下部结构对拱脚的约束并非完全刚性,在这种情况下拱脚约束可以简化为水平和转动弹性约束。采用ANSYS有限元分析软件,在考虑初始缺陷、几何非线性和材料非线性的基础上,针对工字形截面水平和转动弹性支承圆弧钢拱进行了参数化分析。研究了不同荷载工况下水平和转动弹性支承拱的弹塑性极限承载力、极限状态下拱脚的支座位移,对已有的设计公式进行了修正。
圆弧拱;弹塑性极限承载力;弹性支承
0 引言
钢拱形结构作为一种建筑类型,具有轻质高强,韧性、塑性好、结构可靠性高等一系列优点[1]。在实际工程中许多钢拱结构支承于其他结构之上,下部结构对拱脚的约束并非完全刚性,在这种情况下拱的极限承载力会发生什么变化,极限承载情况下的拱脚位移会如何变化是需要系统研究的。
国内外的许多学者对弹性支承拱的稳定和承载力问题进行过许多深入的研究。Bradford et al[2-7]研究了支座沿径向和切向弹性支承的圆弧浅拱在静水压力作用下的平面内几何非线性屈曲性能。童根树和杨洋[8]针对水平弹性支承圆弧钢拱,利用ANSYS进行了平面内极限承载力的研究,考虑了初始缺陷、残余应力以及材料非线性,讨论了弹性支承刚度对拱的平衡路径的影响,分析了4种荷载工况下弹性支承刚度对拱的极限承载力和支座位移的影响,给出了极限承载力和支座位移的拟合公式。黄山和杨洋[9]针对水平弹性支承圆弧钢拱利用ANSYS进行了几何非线性屈曲分析,研究了弹性支承刚度对屈曲模态的影响,然后就长细比、矢跨比、几何初始缺陷对荷载位移曲线的影响进行了分析,给出了水平弹性支承圆弧钢拱的极限承载力以及支座水平位移随弹性柔度系数变化的拟合公式。

图1 拱形钢结构的简化
上述学者的研究针对的拱脚弹性支承形式多是沿径向、切向、水平或转动弹性支承形式。沿径向、切向弹性支承形式难于找到在实际工程中的对应形式,单纯考虑水平或转动弹性支承形式也有一定的局限性,对于水平弹性支承和转动弹性支承同时存在的形式还没有学者做过研究。而在实际的工程中这种支承形式也是比较多见的,如拱形立体桁架和拱形立体刚架可以简化成图1所示的弹性支承形式,包括水平弹性支承kh和转动弹性支承kθ。鉴于上述研究中存在的问题,考虑到弹性支承钢拱在实际工程中的大量应用,以及浅拱(矢跨比γ<0.2)对拱脚支承条件的更高要求,现针对水平和转动弹性支承同时存在的圆弧钢浅拱进行研究。

图2 水平和转动弹性支承圆弧拱分析模型
1 计算模型
采用ANSYS有限元分析软件对水平和转动弹性支承对称圆弧钢拱进行平面内弹塑性稳定分析,其计算模型如图2所示。
圆弧拱的半径为R,半跨圆心角为θ,弧长为S,水平和转动弹性支承刚度分别为kh和kθ。定义拱的长细比为λ=S/2γx,拱截面的回转半径为γx,拱截面面积为A,拱截面惯性矩为Ix。模型建立采用3D二次有限应变Beam189梁单元。分析中参考文献[10]考虑结构的初始缺陷、几何非线性和材料非线性的共同影响。根据李涛[11]在考虑左右水平弹簧刚度的情况下,定义无量纲参数水平弹性支承柔度系数。
(1)
根据文献[3]在考虑左右转动弹性支承刚度kθ1=kθ2相同的情况下,定义无量纲参数转动弹性支承柔度系数
(2)

图3 4种荷载工况
圆弧拱截面为焊接工字形截面:截面高400 mm,翼缘宽200 mm,腹板厚10 mm,翼缘厚12 mm,截面面积A=8 560 mm2,惯性矩Ix=2.24×108mm4。钢材的应力-应变关系取双折线模型,弹性模量E=2.06×105MPa,Et=0.02E,屈服强度fy=235MPa,泊松比ν=0.3。初始缺陷幅值取全跨均布荷载作用下有限元模型的反对称屈曲模态最大位移S/1 000,非对称荷载作用下的拱其缺陷形式按照对称荷载作用下拱缺陷形式来施加。考虑4种荷载工况:全跨均布荷载、半跨均布荷载、跨中集中力、四分点集中力,如图3所示。考虑4种矢跨比γ为0.05、01、0.15、0.2和4种长细比λ为20、70、100、150,无量纲水平弹性支承柔度系数β取10、20、30、40、50、60、70、80以考虑水平弹性支承程度的变化,无量纲转动弹性支承柔度系数α取0.1、1、10。共计对1 536组水平弹性支承和转动弹性支承拱进行分析。
2 弹塑性极限承载力分析
本节就水平和转动弹性支承圆弧拱的弹塑性极限承载力进行研究。图4给出了矢跨比γ=0.1、转动弹性支承柔度系数α=0.1时,4种荷载工况下无量纲弹塑性极限承载力随水平弹性柔度系数β的变化规律,图中qu,e表示水平和转动弹性支承拱的极限承载力,qu,r表示相应固支拱的极限承载力。

图4 qu,e/qu,r-β关系曲线(γ=0.1,α=0.1)
由图4可以看出,随水平弹柔度系数β的增大,水平和转动弹性支承拱极限承载力整体呈降低趋势,且中等长细比下极限承载力降低幅度较大,长细比对均布荷载工况下拱的极限承载力影响要大于集中荷载;对比4种荷载工况下的极限承载力降低规律可以看出,全跨均布荷载下极限承载力降低幅度最大,集中荷载下极限承载力降低幅度较小,且对称荷载下极限承载力降低幅度要大于非对称荷载下的情况。长细比λ=20时,随水平弹性柔度系数的增大,极限承载力并没有降低,原因是由于在这种长细比和矢跨比下,弹性支承圆弧拱可以近似看作拱形梁结构,受力状态已经发生改变,此时结构以受弯为主,对水平弹柔度系数β的变化不敏感,发生的是在弯矩作用下的强度破坏。
图5给出了矢跨比γ=0.1,长细比λ=100时不同转动弹性柔度系数下的极限承载力随水平弹性柔度系数增大的变化规律。从图5中可以看出,转动弹性支承对非对称荷载作用下拱的极限承载力影响显著而对对称荷载作用下拱的极限承载力影响不明显,且全跨均布荷载下水平和转动弹性支承拱极限承载力的降低幅度最大;在水平弹性柔度系数为0~20的范围内,非对称荷载作用下,随着转动弹性柔度系数增大,极限承载力值降低,且在四分点集中荷载下降低幅度最大,如图5(d),经计算弹性支承柔度系数为1时相较弹性支承柔度系数为0.1时,极限承载力降低14.8%,弹性支承柔度系数为10时相较弹性支承柔度系数为1时极限承载力降低14.7%。

图5 不同转动弹性柔度系数下qu,e/qu,r-β关系曲线 (γ=0.1, λ=100)
由图5可知,全跨均布荷载下弹性支承拱极限承载力的降低幅度最大,而且转动弹性支承对全跨均布荷载作用下极限承载力的影响不明显,因此本文给出转动弹性支承为10时,全跨均布荷载下4种矢跨比为0.05、0.1、0.15、0.2时对应的极限承载力降低规律,如图6所示,以此作为所有转动弹性支承拱在全跨均布荷载作用下极限承载力的降低规律。从图6可以看出,矢跨比为0.1时极限承载力降低幅度最大,对于水平弹性柔度系数为0~20的一组,降低幅度为52%。
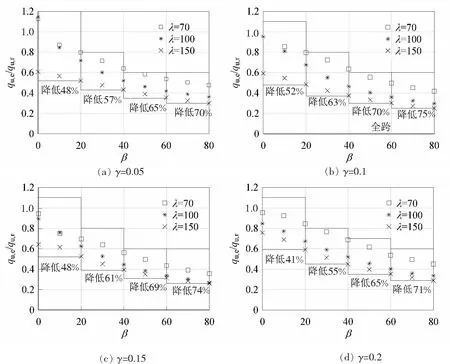
图6 全跨均布荷载下qu,e/qu,r-β降低规律 (α=10)
3 极限状态下拱脚支座位移
图7给出了在转动弹性柔度系数α=0.1时,长细比λ=20、λ=70时全跨均布荷载作用下无量纲的水平位移u/L在不同的矢跨比下随水平弹性柔度系数的变化规律。从图7中可以看出,在水平弹性柔度系数的变化范围内,随着水平弹性柔度系数增大,无量纲水平位移整体上呈单调增加的趋势;矢跨比越大,无量纲水平位移越大。

图7 水平和转动弹性支承拱u/L-β关系曲线(λ=20、λ=70)
图8给出了矢跨比γ=0.1时,圆弧拱在全跨均布荷载作用下无量纲的水平位移随水平弹性柔度系数的变化规律。从图8中可以看出,在水平弹性柔度系数的变化范围内,随着转动弹性柔度系数增大,无量纲水平位移增大;在无转动约束的情况下,转动弹性支承柔度系数大于等于10时,水平和转动弹性支承拱的支座位移和水平弹性支承拱的支座位移接近,转动弹性约束的影响很小,并且转动弹性柔度系数为1时,支座位移与转动弹性柔度系数为10时的支座位移差值不大。

图8 不同α下水平弹性支承拱u/L-β关系曲线 (λ=100、λ=150)
4 设计公式讨论
文献[8]给出了极限承载力降低幅度的拟合公式,并就水平弹性柔度系数给出了临界值,认为小于这个临界值,可以按照铰支拱的设计公式来进行设计。本文按照另一种思路给出设计方法,首先在弹塑性极限承载力降低规律的基础上给出规程[12]中铰支拱设计公式调整系数的估计值。规程[12]中的设计公式如式(3),对于工字形截面的铰支拱α=1.0。参照规程[12]文献[13]中提到在计算稳定时采用的弯矩放大系数法,考虑水平弹性支承的影响时也在弯矩项前乘以一个大于1的数值,调整后的公式如式(4)。
(3)
(4)
对于水平和转动弹性支承同时存在的拱进行设计公式的修正,文献[8]中提到一般拱结构的支座位移u/L不能大于0.01。分析表明在β大于20以后,对于矢跨比为0.2的拱其无量纲支座位移u/L基本上大于0.01,这种形式的拱在实际工程中应用很少,需要加强支座的刚度。故只考虑水平弹性柔度系数为0~20这一组的修正。考虑到水平和转动弹性支承拱极限承载力相较于固支拱降低过大,据此得到的修正公式系数过大,结果过于保守,故取极限承载力降低幅度的1/2作为修正的参考数值,而不是极限承载力降低幅度的下限。为了考虑不同转动弹性柔度系数下修正公式系数不同,由前述分析可知,可以在全跨均布荷载下拱极限承载力降低幅度的基础上,考虑不同转动弹性柔度系数对转动弹性支承拱的不利影响。例如对于转动弹性支承柔度系数为10的拱,根据图6可以得出矢跨比为0.2、0.15、0.1,水平弹性柔度系数为0~20时,稳定承载力降低幅度分别为41%、48%、52%,取三者的平均值计算其极限承载力修正参考数值为:0.5×(0.52+0.48+0.41)/3=0.24,此时修正系数ξ=1/(1-0.24)=1.32。对于转动弹性支承柔度系数为1和0.1的拱设计公式修正系数ξ计算同上,这里就不再赘述。对于矢跨比为0.05的拱,规程[12]中并未给出其相关设计公式,考虑到实际工程应用中,如此小矢跨比的拱加工制造难度大,轴线形式难以保证,这里不再考虑矢跨比为0.05拱的设计。在弹塑性极限承载力降低规律的基础上给出固支拱(α=0.91)设计公式修正系数ξ的估计值,如表1。

表1 水平和转动弹性支承拱设计公式修正系数
对于表1给出的修正系数,通过ANSYS计算来验证其适用性,见图9~图11。从图中可以看出,修正的设计公式是安全的。对比3个图还可以看出,转动弹性支承柔度系数越大,即转动弹性支承刚度越小,数据点越离散。

图9 弹性支承拱稳定极限承载力曲线 (α=0.1)
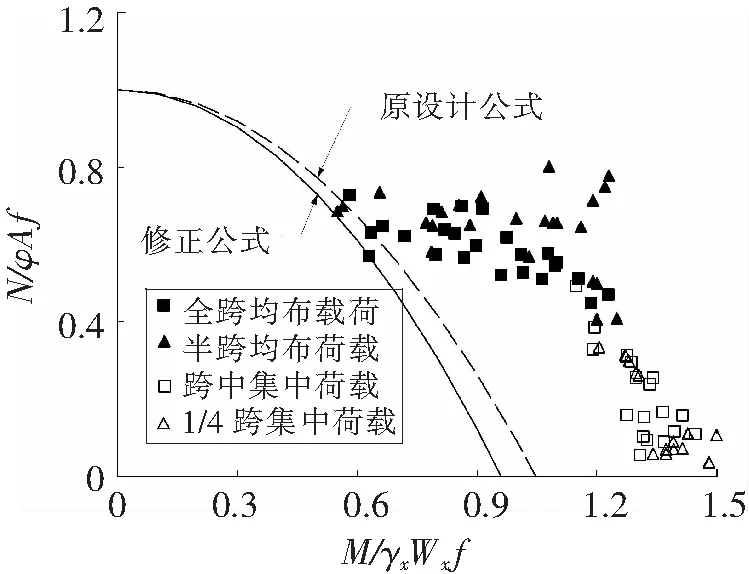
图10 弹性支承拱稳定极限承载力曲线 (α=1)

图11 弹性支承拱稳定极限承载力曲线 (α=10)
5 结论
本文就水平和转动弹性支承圆弧钢浅拱的弹塑性稳定承载力进行了深入的研究,包括弹塑性极限承载力和支座位移随水平弹性柔度系数的变化规律和设计公式的修正,得到以下结论:
(1)全跨均布荷载下拱的极限承载力随水平弹性柔度系数增大的降低幅度最大;在同一转动弹性柔度系数下对称荷载对拱的极限承载影响要大于非对称荷载;在相同的水平弹性柔度系数下,随转动弹性支承柔度系数增大,非对称荷载作用下极限承载力降低显著,对称荷载作用下极限承载力变化不明显,且在四分点集中荷载作用下极限承载力降低幅度最大。
(2)在水平弹性柔度系数0~80的范围内,随着水平弹性柔度系数增大,无量纲水平位移整体上呈单调增加的趋势,且在水平弹性柔度系数为0~20时增加幅度较大,大于20后增幅变小;长细比越大,无量纲水平位移越大。矢跨比对支座水平位移的影响较大,矢跨比越大,支座位移越大。
(3)给出了水平弹性柔度系数为0~20时,水平和转动弹性支承圆弧拱设计公式的修正方法。
(4)对于水平和转动弹性支承拱的设计可以通过设计公式(4)和支座位移控制条件来给出设计方法,如果满足公式(4),同时满足位移控制条件则认为设计是安全的,在不满足的条件下需要通过加强支座的刚度来达到要求。
[1]陈绍蕃.钢结构设计原理[M].北京:科学出版社,2001.
[2]Pi YL, Bradford MA, Tin-Loi F. Nonlinear analysis and buckling of elastically supported circular shallow arches[J].International Journal of Solids and Structures,2007,44(7/8):2401-2425.
[3] Pi YL, Bradford MA, Tin-Loi F. Nonlinear in-plane buckling of rotationally restrained shallow arch under a central concentrated load[J].International Journal of Non-Linear Mechanics,2008,43(1):1-17.
[4] Pi YL, Bradford MA. Non-linear in-plane post buckling of arches with rotational end restraints under uniform radial loading[J].International Journal of Non-Linear Mechanics,2009,44(9):975-989.
[5] Pi YL, Bradford MA. Nonlinear analysis and buckling of shallow arches with unequal rotational end restraints[J].Engineering Structures,2013,46(1): 615-630.
[6] Bradford MA, Wang T, Pi YL. In-plane stability of parabolic arches with horizontal spring supports, I: Theory[J].Journal of Structural Engineering,2007,133(8):1130-1137.
[7] Pi YL, Bradford MA, Tin-Loi F. Geometric and material nonlinear analysis of elastically restrained arches[J].Engineering Structures,2007,29(3):283-295.
[8]杨洋,童根树.水平弹性支承圆弧钢拱的平面内极限承载力研究[J].工程力学,2012,29(3):45-53.
[9]黄山,杨洋.水平弹性支承圆弧钢拱的几何非线性稳定研究[J].建筑结构,2013,43(15):131-135.
[10]信丽华,林玉森,段树金.初始几何缺陷对钢管混凝土拱桥极限承载力的影响[J].石家庄铁道学院学报:自然科学版,2009,22(3):10-13.
[11]李涛.弹性支承圆弧钢浅拱平面内非线性稳定及设计方法[D].天津:天津大学,2015.
[12]中华人民共和国住房和城乡建设部.JGJ/T249—2011拱形钢结构技术规程[S].北京:中国建筑工业出版社,2011.
[13]李运生,张彦玲,王慧东.拱桥稳定分析的规范方法与建议[J].石家庄铁道学院学报,2002,15(3):60-64.
Elastic-plastic Ultimate Bearing Capacity of Steel Circular Arches with Elastic Supports
Lu Peng1, Li Tao2, Lu Yan1,3
(1.School of Civil Engineering, Tianjin University, Tianjin 300072, China;2. Shandong Tongyuan Design Group Co. Ltd, Jinan 250000, China;3. Key Laboratory of Coast Civil Structure Safety of China Ministry of Education, Tianjin University, Tianjin 300072, China)
Many arch structures are supported against other structures in practical engineering. The constraint which is provided by the substructure is not perfectly rigid so that the constraint can be equivalently replaced by horizontal spring and rotational spring. The parametric analysis of I-section circular arch with horizontal and rotational elastic support is conducted by the finite element analysis software ANSYS, considering the initial defects, geometrical nonlinearity, and material nonlinearity. The elastic-plastic ultimate bearing capacity of the horizontal and rotational elastic support arch under different load conditions and the support displacement of arch foot at limit state are studied in this paper. The existing design formula are revised through a large number of finite element calculations.
circular arches;elastic-plastic ultimate bearing capacity;elastic supports
2015-11-16 责任编辑:车轩玉
10.13319/j.cnki.sjztddxxbzrb.2016.04.04
卢鹏(1988-), 男,硕士研究生,主要从事钢结构的研究。E-mail: 8094288@qq.com
TU391
A
2095-0373(2016)04-0021-07
卢鹏,李涛,芦燕.弹性支承圆弧钢浅拱弹塑性极限承载力分析[J].石家庄铁道大学学报:自然科学版,2016,29(4):21-27.
