压头作用下岩石破碎过程的细观模拟

李守巨，李 德，于 申

(1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.哈尔滨电机厂有限责任公司，黑龙江 哈尔滨 150000)



压头作用下岩石破碎过程的细观模拟

李守巨1，李 德2，于 申1

(1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.哈尔滨电机厂有限责任公司，黑龙江 哈尔滨 150000)

采用平行粘结细观本构模型，在岩石颗粒尺度上研究了压头侵入岩石的破坏过程。分析讨论了岩石材料平行粘结模型细观参数与宏观力学参数之间的映射关系。为了实现表征颗粒连接破坏模式，应用FISH语言编写一个伺服程序，检测每个颗粒连接的受力状态。依据所建立的颗粒连接破坏准则，并对每个颗粒连接进行破断与否的评估，实现描述颗粒连接的破坏功能。研究表明，在压头垂直压力作用下，岩石试件内形成了3条主环向拉力链，它与宏观的小主应力方向一致。环向拉力链最大影响深度随着压头压入深度的增加而增加。与此同时，出现了几条径向压力链，它与宏观的大主应力方向基本一致。岩石试件裂纹是由环向拉应力和剪应力大于颗粒平行连接胶结材料的强度引起的。

岩石试件；破碎过程；参数估计;细观模拟；压头侵入；平行粘结模型

0 引 言

离散元方法是当今非连续介质力学数值方法中应用于岩石和混凝土等脆性材料的最广泛而且最有效的方法之一。其最大特点是可以反映岩石块体之间的接触面滑移、分离以及倾覆旋转，表征岩体内部节理、裂隙和断层等非连续特性，同时还能够计算块体内部的变形和应力，尤其对于描述岩石破坏过程的细观机制具有内在的优越性。已经广泛应用于岩石边坡稳定性分析、地下厂房围岩稳定性和破坏过程模拟、混凝土结构的裂缝扩展、破坏与倒塌过程分析、盾构机滚刀破岩过程分析和混凝土大坝及其基础破坏机制等岩石工程领域。Gu[1]提出了刚体-弹簧模型模拟混凝土材料初始缺陷和骨料分布特性，所建立的离散元模型包括粗骨料、细骨料、砂浆和粘结界面，并且考虑了这些材料的随机分布特性。James[2]研究了非均质岩石细观裂纹的分布特性，提出了颗粒断裂的破坏准则。Gray[3]回顾了地质结构体的有限元和离散元建模问题，分析了有限元、离散元和有限差分法的在表征非连续地质体力学特性的适用性。Shmulevich[4]应用离散元方法(PFC)模拟了切刀与土体之间的相互作用特性，研究表明该方法模拟的结果与实验结果基本一致，其目的在于通过优化切刀的形状，提高切刀破土的能量利用率。Ono[5]采用三维离散元方法模拟了切土工具与土体之间的作用机制，讨论了6种离散元形状对数值模拟结果的影响，并将实验结果与模拟结果进行了对比分析。Ucgul[6]采用三维离散元模型模拟了切刀切土的破坏过程，重点分析了无内聚力散体砂土模型参数估计问题，讨论了线性和非线性接触模型的差异性和适用性。Arena[7]提出了一种新方法用于定量计算实验过程中岩石细观裂纹，该方法以二维数字图像为基础，对于定量分析岩石试件表面裂纹的演化过程具有借鉴和参考价值。Mak[8]介绍了用于表征土体与切刀之间相互作用的离散元模型，讨论了细观模型中某些参数的简化估计方法，并且进行了切刀切土的实验和模拟分析研究。Asaf[9]提出了如何根据切刀破土实验数据进行离散元模型参数校准问题。Innaurato[10]采用实验和数值模拟方法研究了TBM滚刀的破岩过程，建立了滚刀贯入深度与贯入力之间的关系，研究了滚刀作用下岩石的剪切破坏问题。从以上相关研究工作中可以看出，采用离散元方法研究土体材料破坏过程所进行的工作较多，而研究岩石材料细观破坏过程的工作相对较少。与此同时，如何较为准确估计岩石材料的细观模型参数是制约离散元方法解决工程实际问题的瓶颈。岩石的力学行为由其内在的细观结构和模型参数决定，尤其是岩石细观裂纹及其演化和发展过程。笔者的目的在于在岩石颗粒尺度上研究压头作用下的岩石破坏过程，揭示岩石破碎漏斗的细观形成机制。

1 岩石材料平行粘结模型细观参数估计

岩石是多种矿物和胶结物组成的一种高度不均匀材料，在细观层次上表现在颗粒、粘结物和结构面等力学特性的随机分布特点。颗粒流(Particle Flow Code)方法是由Cundall和Strack提出的模拟球形颗粒运动与相互作用的细观离散元方法。该方法已经应用到岩石、土体和混凝土材料的力学特性研究中，着重从细观力学角度揭示材料的损伤和断裂机理。颗粒接触刚度模型包括线性颗粒接触刚度模型和Herz-Mindlin非线性接触模型等。如图1所示，颗粒接触刚度模型参数包括法向刚度(kn)、切向刚度(ks)和摩擦系数(f)以及阻尼(η)等。

图1 颗粒接触刚度模型Fig.1 Contact model of particles

图2 岩石材料平行粘结模型Fig.2 Parallel bond model for rock materials

平行粘结模型(Parallel bond model)用于模拟岩石和混凝土材料(非散体材料)的开裂问题，Azevedo提出了其简化模式[11]，如图2所示，岩石的细观模型参数还包括：颗粒之间胶结材料的法向刚度(kpn)和切向刚度(kps)、胶结材料切向剪切强度(τs)和法向抗拉强度(σt)，以及胶结圆环的半径因子(λ)。需要说明的是，颗粒之间胶结材料的切向剪切强度(τs)和法向抗拉强度(σt)与岩石宏观实验的剪切强度和抗拉强度并不是一个概念，但二者之间应该具有某种相关性，因为平行粘结模型将颗粒之间的粘结简化成了一个等效的圆盘。

平行粘结模型法向刚度kn为[12]

kn=2tEc,

(1)

式中t为宽度，对于2维模型，t=1；Ec为颗粒接触变形模量，近似取为岩石宏观实验的弹性模量E，取Ec=43 GPa.切向刚度ks与法向刚度的关系为

ks=Rckn,

(2)

式中Rc为颗粒切向刚度与法向刚度的比，研究表明，这两个值近似相等[13]，取Rc=1.0.颗粒之间的细观摩擦系数f与宏观内摩擦角φ的近似关系为[14]

(3)

颗粒之间胶结材料的法向刚度kpn为

(4)

式中 Epc为平行粘结变形模量；RA和RB分别为颗粒A和B的半径。平行粘结颗粒之间胶结材料的切向刚度kps为

kps=Rpkpn,

(5)

式中 Rp为平行粘结模型切向刚度与法向刚度的比，取Rp=1.平行粘结模型细观抗拉强度与宏观内聚力c和内摩擦角φ的关系为[8]

σt=c×cotφ,

(6)

式中 σt为平行粘结模型细观法向抗拉强度。平行粘结细观抗剪强度与宏观内聚力的关系为[8]

τs=c,

(7)

式中 τs为颗粒之间胶结材料的切向剪切强度；颗粒之间固定平行粘结半径因子取为λ=0.5.颗粒之间粘结环半径Rb为

(8)

模拟的岩石试样为中晶大理岩，其粒径为1～4 mm，颗粒流模型颗粒的直径为2 mm，岩石试样的宏观力学参数见表1，表2为岩石细观参数估计值。

表2 岩石试样的细观参数估计值

2 压头作用下岩石破碎过程细观模拟

岩石是由多种矿物和胶结物组成的非均匀体，并且含有大量的天然节理和微裂隙。天然岩体中的断层、节理和裂隙的随机分布，其空间几何和力学参数的分布具有统计特征。在长期的地质作用和水文环境下岩体产生的微裂纹、缺陷和孔隙，在外界荷载作用下，在岩石矿物颗粒和胶结物结合面上存在初始微裂纹损伤，在破坏机制上存在局部化现象，并导致应变软化的本构特性[14]。

在单轴压缩情况下，岩石试样的破坏过程是随机分布强度参数的岩石颗粒的刚度逐渐劣化的结果。从连续介质力学观点分析，岩石试样的破坏方式就其力学本质可以归结为压缩破坏、拉伸破坏和剪切破坏。为了实现表征颗粒连接力学破坏模式，应用FISH语言编写一个伺服程序，检测每个颗粒连接的受力状态，依据所建立的颗粒连接力学破坏准则，并对每个颗粒连接进行破断与否的评估，进而实现描述颗粒连接的破坏功能。

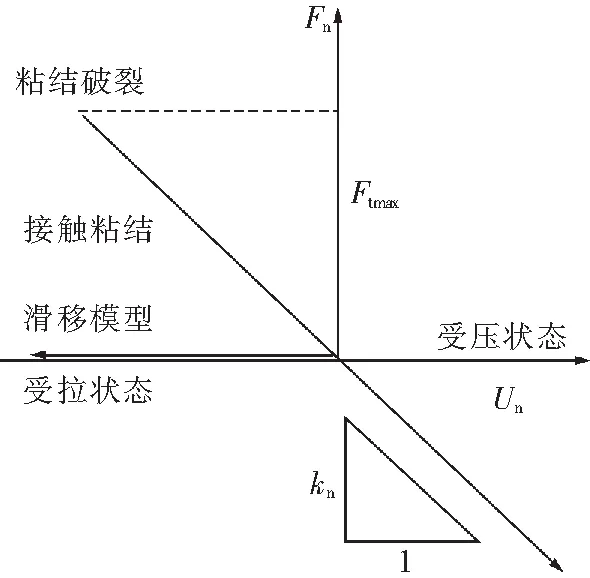
图3 平行粘结模型法向力与法向位移之间的本构关系Fig.3 Constitutive relation between normal force and displacement for parallel bond model

图4 平行粘结模型切向力与切向位移之间的本构关系Fig.4 Constitutive relation between tangential force and displacement for parallel bond model

如图3所示，颗粒之间法向接触力Fn与法向相对位移之间的关系为

Fn=knUn，

(9)

式中Un为法向相对接触位移，即2个球的重叠量，其为割线模量，kn建立了总体法向力与总体法向位移之间的线性关系。

如图4所示，切向接触力以增量形式计算，其计算公式为

ΔFs=-ksΔUs,

(10)

式中ks为切向刚度，其为切线模量；ks建立了切向力增量ΔFs与切向位移增量ΔUs之间的线性关系。颗粒粘结的拉应力破坏准则为

叶总拿过玉坠仔细把玩了一番，又认真咀嚼起王祥的话。钱总则是和王祥一起纳起闷来。良久，叶总突然笑了起来，他把玉坠递还给王祥：

(11)

式中Ftmax为颗粒粘结所承受的极限拉力。颗粒粘结的剪应力破坏准则为

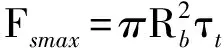
(12)

式中 Fsmax为颗粒粘结所承受的极限剪力。当颗粒粘结剪切破坏后，并且颗粒之间处于受压状态时，其滑动阻力Fsf为

Fsf=fFn(Fn>0).

(13)

如图5所示，金属压头弹性模量为200GPa，刚性压头利用墙体模拟，设定压头尺寸为20mm×20mm，赋予压头的法向刚度取为400GN/m，侵入速度为0.001mm/step，总侵入深度为10.0mm.岩石试样的几何尺寸为200mm×100mm，岩石颗粒密度为2 700kg/m3.模型边界利用墙体模拟[15]，令其法向刚度等于颗粒法向刚度。设定岩石颗粒粒径为2.0mm，颗粒数目为5 000个。随着岩石试样的加载过程，岩石材料将不断产生新的裂纹，部分颗粒之间的粘结将发生断裂力学形式的破断，某些颗粒配位数也将随之不断变化。

图5 压头侵入深度2 mm时的力链分布Fig.5 Force chains in rock specimen under 2 mm penetration depth

图6 压头侵入深度4 mm时的力链分布Fig.6 Force chains in rock specimen under 4 mm penetration dept

在平行粘结力链图中，深色部分表示颗粒之间处于受拉状态，黑色部分表示颗粒之间处于受压状态。从图5中可以看出，在压头垂直压力作用下，在岩石试件内，形成了3条主环向拉力链，它与宏观的小主应力方向一致，环向拉力链最大影响深度约为30mm.同时，出现了几条径向压力链，它与宏观的大主应力方向基本一致。

从图6中可以看出，随着压头侵入深度的增加，环向拉力链最大影响深度扩展到约为42mm；主环向拉力链发展得更加明显。

图7 压头侵入深度6 mm时的力链分布Fig.7 Force chains in rock specimen under 6 mm penetration depth

图8 压头侵入深度8 mm时的力链分布Fig.8 Force chains in rock specimen under 8 mm penetration depth

从图7中可以看出，随着压头侵入深度的增加，环向拉力链最大影响深度扩展到约为56mm；在压头下部附近出现了一部分破碎区。

对比图7，8和9可以发现，压头下面的破碎区域(浅色区域)随着压头侵入深度的增加而逐渐增加，直至形成破碎漏斗。

图9 压头侵入深入10 mm时的力链分布Fig.9 Force chains in rock specimen under 10 mm penetration depth

从图9中可以发现，在压头正下方形成了一个明显的破碎漏斗(浅色区域)，破碎漏斗的角度为70左右。岩石是一种典型的非均质和准脆性材料[16]，岩石晶粒和初始缺陷的分布具有随机性和不确定性，在荷载作用下，各组分成分的刚度差异很大，使得对力的传递响应和自身变形的差异，导致在岩石内部应力场和应变场分布极不均匀，产生局部应力集中，在初始缺陷或弱结合面区域产生微裂纹，且裂纹的扩展路径具有明显的非对称性。岩石中裂纹扩展路径强烈依赖于岩石材料的非均匀性，材料的非均匀性对裂纹的贯通和抑制有着重要的影响。在细观尺度上，岩石内部所含有的晶粒和胶结物的力学性质差异较大，岩石材料具有明显的非均匀性。

3 结 论

1)岩石材料在弹塑性变形直至破坏过程中，其宏观体积响应只是各种微结构之间相互作用的平均结果，变形的主要机制是微裂纹成核和增长及其聚集而生成细观裂纹、扩展成宏观裂纹、直至宏观破坏。由于岩石(岩体)内含有大量的初始缺陷(节理、层理、微裂纹等)，连续介质力学方法对于表征岩石的这些非连续特性存在着固有的缺点，尤其是分析裂纹群扩展过程时遇到的困难更加突出，离散元方法为解决这类难题提供了新的途径；

2)采用非连续介质力学数值方法，发展岩石的细观力学模型有助于从材料破坏机理的层面上对宏观岩石破坏过程进行理解和解释。研究表明，在压头垂直压力作用下，在岩石试件内，形成了3条主环向拉力链，它与宏观的小主应力方向一致。环向拉力链最大影响深度约随着压头压入深度的增加而增加。与此同时，出现了几条径向压力链，它与宏观的大主应力方向基本一致；

3)岩石试件裂纹是由环向拉应力和剪应力大于颗粒平行连接胶结材料的强度引起的。压头作用下岩石的破坏特性细观模拟分析成果，为TBM滚刀破岩分析、滚刀优化布置和滚刀形状设计提供了一种可以借鉴的方法；

4)如何精确定量确定岩石细观模型中的参数是制约离散元方法发展和应用的瓶颈问题之一。由于岩石颗粒大多在mm量级，在该尺度上直接测量力学参数是非常困难的。如果能够在岩石试样宏观尺度上进行实验，并且基于宏观实验数据进行力学细观模型参数反演，将是一项十分有意义的工作。

References

[1]GUXiang-lin，LIHong，WANGZhuo-lin，etal.Amodifiedrigid-body-springconcretemodelforpredictionofinitialdefectsandaggregatesdistributioneffectonbehaviorofconcrete[J].ComputationalMaterialsScience，2013，77(3)：355-365.

[2]JamesPM，FordM，JivkovAP.Anovelparticlefailurecriterionforcleavagefracturemodelingallowingmeasuredbrittleparticledistributions[J].EngineeringFractureMechanics，2014，121-122(1)：98-115.

[3]GrayGG，MorganJK，SanzPF.Overviewofcontinuumandparticledynamicsmethodsformechanicalmodelingofcontractionalgeologicstructures[J].JournalofStructuralGeology，2014，59(2)：19-36.

[4]ShmulevichI，AsafZ，RubinsteinD，Interactionbetweensoilandawidecuttingbladeusingthediscreteelementmethod[J].Soil&TillageResearch，2007，97(1)：37-50.

[5]OnoI，NakashimaH，ShimizuH，etal.Investigationofelementalshapefor3DDEMmodelingofinteractionbetweensoilandanarrowcuttingtool[J].JournalofTerramechanics，2013，50(4)：265-276.

[6]UcgulM，FielkeJM，Saunders.Three-dimensionaldiscreteelementmodelingoftillage：Determinationofasuitablecontactmodelandparametersforacohesionlesssoil[J].BiosystemsEngineering，2014，121(2)：105-117.

[7]ArenaA，PianeCD，SaroutJ.Anewcomputationalapproachtocracksquantificationfrom2Dimageanalysis：Applicationtomicro-cracksdescriptioninrocks[J].Computers&Geoscience，2014，66(1)：106-120.

[8]MakJ，ChenY，SadekMA.Determiningparametersofadiscreteelementmodelforsoil-toolinteraction[J].Soil&TillageResearch，2012，118(5)：117-122.

[9]AsafZ，RubinsteinD，ShmulevichI.Determinationofdiscreteelementmodelparametersrequiredforsoiltillage[J].Soil&TillageResearch，2007，92(1-2)：227-242.

[10]InnauratoN，OggeriC，OrestePP，etal.ExperimentalandnumericalstudiesonrockbreakingwithTBMtoolsunderhighstressconfinementrockmech[J].RockMechanicsandRockEngineering，2007，40(5)：429-451

[11]AzevedoNM，LemosJV，AlmeidaJR.Influenceofaggregatedeformationandcontactbehaviorondiscreteparticlemodelingoffractureofconcrete[J].EngineeringFractureMechanics，2008，75(6)：1 569-1 586.

[12]PotyondyDO，CundallPA.Abonded-particlemodelforrock[J].InternationalJournalofRockMechanicsandMiningSciences，2004，41(8)：1 329-1 364.

[13]李守巨，李 德，于 申.基于宏观实验数据堆石料细观本构模型参数反演[J].山东科技大学学报，2015，34(5)：20-26.

LIShou-ju，LIDe，YUShen.Meso-parametersInversionofconstitutivemodelforrock-fillmaterialsbasedonmicroexperimentaldata[J].JournalofShandongUniversityofScienceandTechnology，2015，34(5)：20-26.

[14]孙其诚，厚美瑛，金 峰.颗粒物质物理与力学[M].北京：科学出版社，2011.

SUNQi-cheng，HOUMei-ying，JINFeng.Physicalandmechanicalsofgranularmaterial[M].Beijing：SciencePress，2011.

[15]乔卫国，杨 麟，李大勇.高频振动沉桩的离散元模拟分析[J].西安科技大学学报，2012，32(5)：604-609.

QIAOWei-guo，YANGLin，LIDa-yong.Numericalanalysisofpilesdrivingbyhighfrequencyvibrationusingdiscreteelementmethod[J].JournalofXi’anUniversityofScienceandTechnology，2012，32(5)：604-609.

[16]马文伟，赵光明，孟祥瑞.岩石SHPB劈裂分析理论研究[J].西安科技大学学报，2013，33(5)：283-290.

MAWen-wei，ZHAOGuang-ming，MENGXiang-rui.TheoreticalstudyforsplittinganalysisofrockusingSHPB[J].JournalofXi’anUniversityofScienceandTechnology，2013，33(5)：283-290.

Meso-simulation for fracturing process of rock specimen under action of indenter

LI Shou-ju1，LI De2，YU Shen1

(1.StateKeyLaboratoryofStructuralAnalysisforIndustrialEquipment，DalianUniversityofTechnology，Dalian116024，China；2.HarbinElectricMachineryCompanyLimited，Harbin15000，China)

The parallel bond model in discrete element method is used to simulate the fracturing process of rock specimen under action of indenter.The nonlinear mapping relations between meso-parameters of constitutive model and macro mechanical parameters of rock specimen are analytically bridged.In order to characterize the fracture mode between the bonds of parcels each other，the serving program is coded with FISH language，and the stress states for every bound is checked.Based on the proposed fracturing criterion for the bonds of parcels，the evaluation for whether exists fracture between the bonds of parcels is performed.The investigation shows that under the action of vertical indenter，the tree tensile force chains are produced in circumferential direction，and their directions are same as the directions of the minor principal stress.The directions of radial compressive force chains are same as the directions of the major principal stress.The cracks in rock specimen are induced by tensile force in circumferential direction and shear force when the tensile stress or shear stress is larger than material strength.

rock specimen；fracturing process；parameter evaluation；meso-simulation；indenter penetration；parallel bond model

10.13800/j.cnki.xakjdxxb.2016.0602

1672-9315(2016)06-0769-06

国家重点基础研究发展计划(2015CB057804)；国家自然科学基金(11572079)；工业装备结构分析国家重点实验室开放基金(S14206)

李守巨(1960-)，男，辽宁沈阳人，教授，博士，E-mail:lishouju@dlut.edu.cn

2016-05-10 责任编辑：杨泉林

TU 443

A