新型复合摆线外啮合圆柱齿轮副的传动特性分析

韩振华,石万凯,肖洋轶,徐浪

(重庆大学机械传动国家重点实验室,400030,重庆)



新型复合摆线外啮合圆柱齿轮副的传动特性分析

韩振华,石万凯,肖洋轶,徐浪

(重庆大学机械传动国家重点实验室,400030,重庆)

基于传统摆线成形原理,提出了摆线成形的二连杆等效机构转化方法,得到了n+1连杆机构生成广义n阶摆线轨迹的运动规律,推导并建立了可用于齿轮传动的新型四阶复合摆线齿廓方程;基于微分几何及共轭啮合理论,推导了复合摆线齿廓的共轭齿廓方程,分析了该新型齿轮副的压力角、曲率、重合度、滑动率等啮合特性;进行了齿轮副三维实体模型的精确构建,并利用有限元法分析了该齿轮副的强度特性。研究表明:当齿高确定时,分度圆压力角由齿形调控系数f1控制;齿廓曲线是由凹凸弧组成的光滑曲线,且传动过程始终为凹凸齿面线接触啮合传动,理论上具有较高的接触疲劳强度;相对于渐开线齿轮,复合摆线齿轮副具有较高的重合度、极小的滑动率以及较高的弯曲强度和接触强度。最后,加工了齿轮副试验样件,并在FZG齿轮试验机上测试了不同工况下的传动效率,结果表明:复合摆线齿轮副的传动效率随加载扭矩在97.30%～99.00%范围内呈正相关变化,且高于同工况下的渐开线齿轮副,具有工程应用价值。

复合摆线齿轮;齿轮传动;啮合原理;传动特性

齿轮作为动力传动装置的关键基础件,在采煤机截割传动机构、卫星天线指向机构、直升机旋翼主减速器、高速列车齿轮箱及舰船推进传动系统等关键装备中发挥着不可替代的作用。近年来,上述装备领域对齿轮传动系统提出了高功率密度、高速、高精度及高可靠性等高性能要求,而高性能齿轮的主要技术指标集中体现于更高的弯曲强度、接触强度和传动效率[1]。共轭齿廓曲线在很大程度上决定着齿轮副的传动性能,开展新型齿廓共轭传动理论研究,可以为新型高性能齿轮研究提供很好的技术保障,也是提高齿轮传动性能的重要理论基础。

随着人们对摆线齿形研究的重视,越来越多的学者开始研究能用于外啮合动力传动的新型摆线类齿廓,比较有影响的是封闭式泛摆线齿廓[9]及新型短幅外摆线和平摆线组合齿廓[10],这2种新型摆线齿廓对相关研究有着重要的指导作用。另外,薛云娜等研究了摆线齿条和滚柱齿轮传动机构,该机构具有双向零间隙高精度传动的优点[11]。总体来说,国内外对可用于动力传动的外啮合摆线类齿廓研究得相对较少,研究具有动力传动优势的新型摆线类齿廓曲线对提高齿轮传动性能具有重要意义。

本文在分析传统摆线成形原理的基础上,对其成形轨迹进行了二连杆等效机构转化,并提出了n+1连杆机构的广义n阶摆线运动规律;在此基础上,分析了新型复合摆线齿廓的成形原理,得到了复合摆线可用于齿轮传动的条件,提出了新型复合摆线齿轮的传动形式,并建立了复合摆线齿廓曲线共轭啮合理论;从压力角、曲率、重合度和滑动率等方面研究了复合摆线齿轮副的传动特性;建立了精确的实体模型,利用有限元法分析了齿轮副的强度特性;最后,加工出了齿轮副试验样件,利用FZG齿轮试验机测试了齿轮副的传动效率。

1 复合摆线成形原理

1.1 摆线成形原理及连杆运动等效转化

摆线成形方法主要有外切外滚法、内切内滚法、内切外滚法[12]以及包络运动法[2]。对于外切外滚法和内切内滚法,如图1所示,滚圆(半径为rg,圆心为ov)沿着基圆(半径为r0,圆心为oc)外切或内切做纯逆时针滚动时,滚圆上一点或与滚圆固结的一点M形成的轨迹即为摆线。图1中,αc为展形起始角,起始位置ocov与x轴重合,M点位于ocov所在的直线上。外切外滚法生成外摆线,轨迹方程为式(1);内切内滚法生成内摆线,轨迹方程为式(2)。

(1)

(2)

式中:e1=|o1M|=λ1rg,λ1为幅长系数;z为整数,z=r0/rg,表示摆线的周期数;符号“±”“∓”表示起始位置M点与直线ocov的位置关系,若M点位于ov的右边,方程(1)、(2)均取上面的符号,若M点位于ov的左边,方程(1)、(2)均取下面的符号。

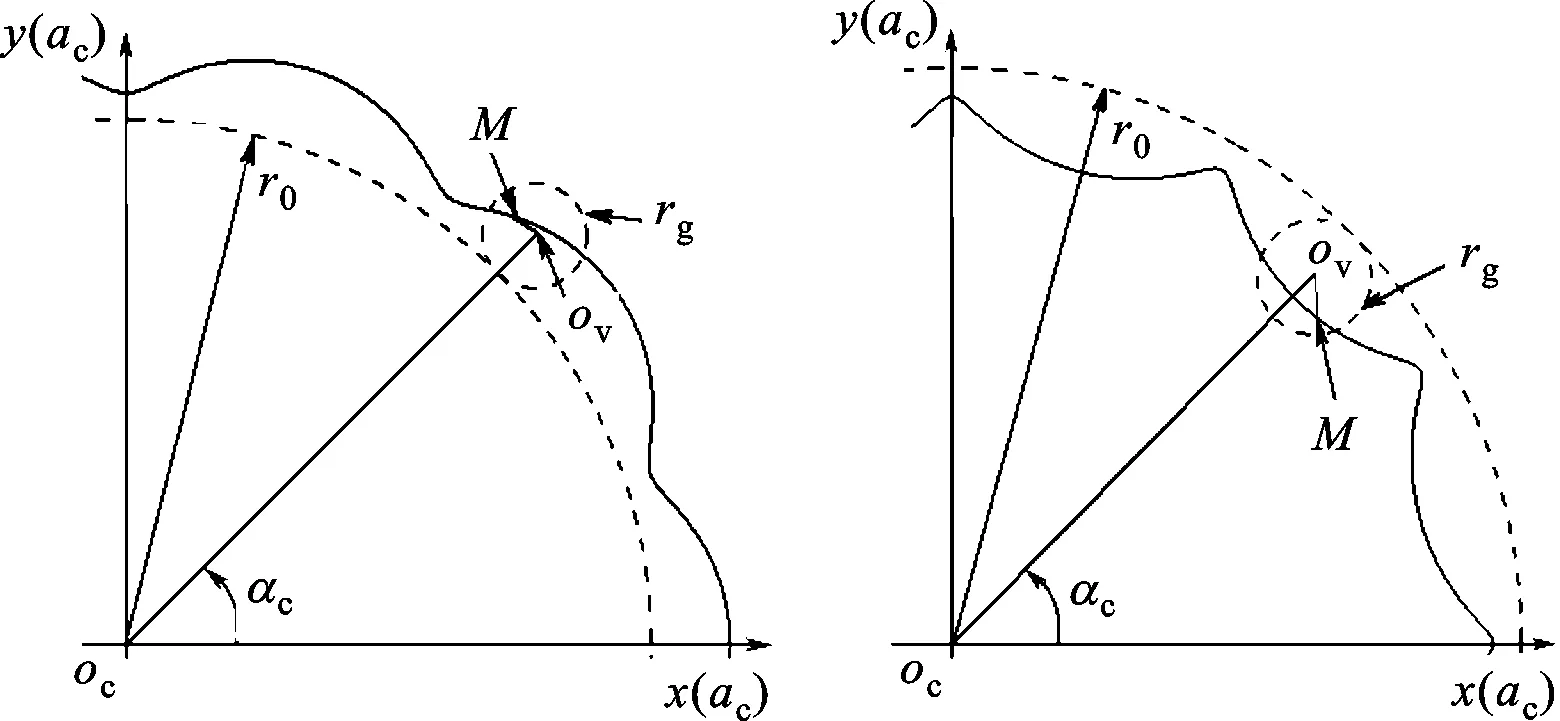
(a)外摆线 (b)内摆线图1 摆线成形原理

若M点在滚圆上,即λ1=1,产形轨迹为等幅外摆线和等幅内摆线;若M点在滚圆内,即0<λ1<1,产形轨迹分别为短幅外摆线和短幅内摆线;若M点在滚圆外,此时λ1>1,则相应地生成长幅外摆线和长幅内摆线。为便于描述,将上述6种摆线统称为广义摆线。

对广义摆线成形运动进行等效机构转化,如图2所示,广义摆线的成形原理可看作是二连杆机构从动杆ovM上M点的运动轨迹。图2中,ocov为连架杆,ovM为从动杆。由M点的轨迹方程可以看出,摆线的几何形状主要由r0、rg和λ1控制,由于控制参数单一,限制了摆线齿廓的应用范围,使其只在摆线针轮行星传动、钟表齿轮和转子泵等特殊领域得以应用。

图2 摆线成形原理的二连杆机构等效转化

1.2 连杆机构的n阶摆线运动

为使摆线齿廓能有效地用于平行轴外啮合动力传动,需增加摆线齿形的调控参数,改变摆线的几何特性,增加齿高和重合度,以增强传动的平稳性。基于摆线成形的二连杆等效机构转化方法,将二连杆运动机构扩展到n+1连杆运动机构来构建新型摆线曲线,如图3所示。在图3中,运动起始位置各连杆的端点An-1依次位于An的左端,运动方向均为逆时针,en为连杆长度,ωi为各连杆的角速度(i=1～n+1),αn为各连杆转动时间t后的转角。将n+1连杆机构末端运动轨迹定义为广义n阶摆线,轨迹方程的复数和指数形式为

(3)

将方程(3)写成参数方程形式

(4)

根据连杆机构的几何特性,当连杆机构各杆的长度确定时,运动轨迹具有唯一性,即改变各连杆的运动起始位置只与式(4)中en前的符号有关,不影响机构末端的整体运动轨迹。

将式(4)定义为广义n阶摆线方程。根据定义可知,1.1节中的广义摆线均可看作一阶摆线。

图3 n+1连杆运动与广义n阶摆线成形原理

1.3 二阶、三阶与四阶复合摆线

为从根本上改变摆线的几何特性,在二连杆运动形成一阶摆线的基础上,参照广义n阶摆线,当三连杆、四连杆与五连杆机构所连接的各圆依次逆时针做内滚、外滚运动时,连杆末端运动形成的周期性轨迹曲线称为二阶、三阶与四阶复合摆线,根据广义摆线、一阶摆线和广义n阶摆线的运动规律,可得到3种复合摆线的曲线方程形式为

(5)

式中:r1、c1、cv1、c2与cv2为各连杆的长度;αt为起始转角;z为曲线周期数。当cv1=c1≠0、cv2=c2=0时,式(5)表示二阶复合摆线;当cv1=c1≠0、c2≠0、cv2=0时,式(5)表示三阶复合摆线;当cv1=c1≠0、cv2=c2≠0时,式(5)表示四阶复合摆线。暂不考虑顶隙系数c*,可求得相应的复合摆线齿廓参数,如表1所示。

表1中,r=0.5mz(m为模数)。对表1中的齿廓参数进行分析,可得到以下结果。

(1)对于三阶复合摆线,当分度圆确定时,c1主要控制齿形高度,故将c1定义为齿高调控参数,令

c1=h1m

(6)

式中:h1定义为齿高系数。

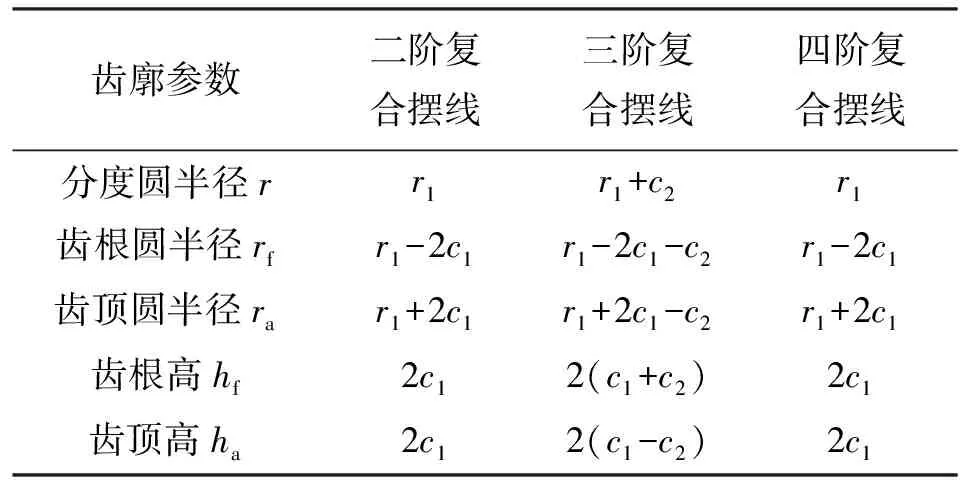
表1 复合摆线齿廓参数

(7)

联立式(6)、式(7)推导可得

(8)

(9)

(3)对于四阶复合摆线,当齿高确定时,通过调节c2可以控制齿形的几何形状,故c2定义为齿形调控参数,令

c2=f1c1

(10)

式中:f1定义为齿形调控系数,通过调节f1可以优化复合摆线的几何特性。根据式(10)可求得

(11)

取模数m=4 mm,齿数z=24,c1=2 mm,可分别求得图4中f1=0.01,0.05,0.1时的四阶复合摆线。从图4可以看出,齿形调控系数f1的变化能显著改变齿形的几何形状。

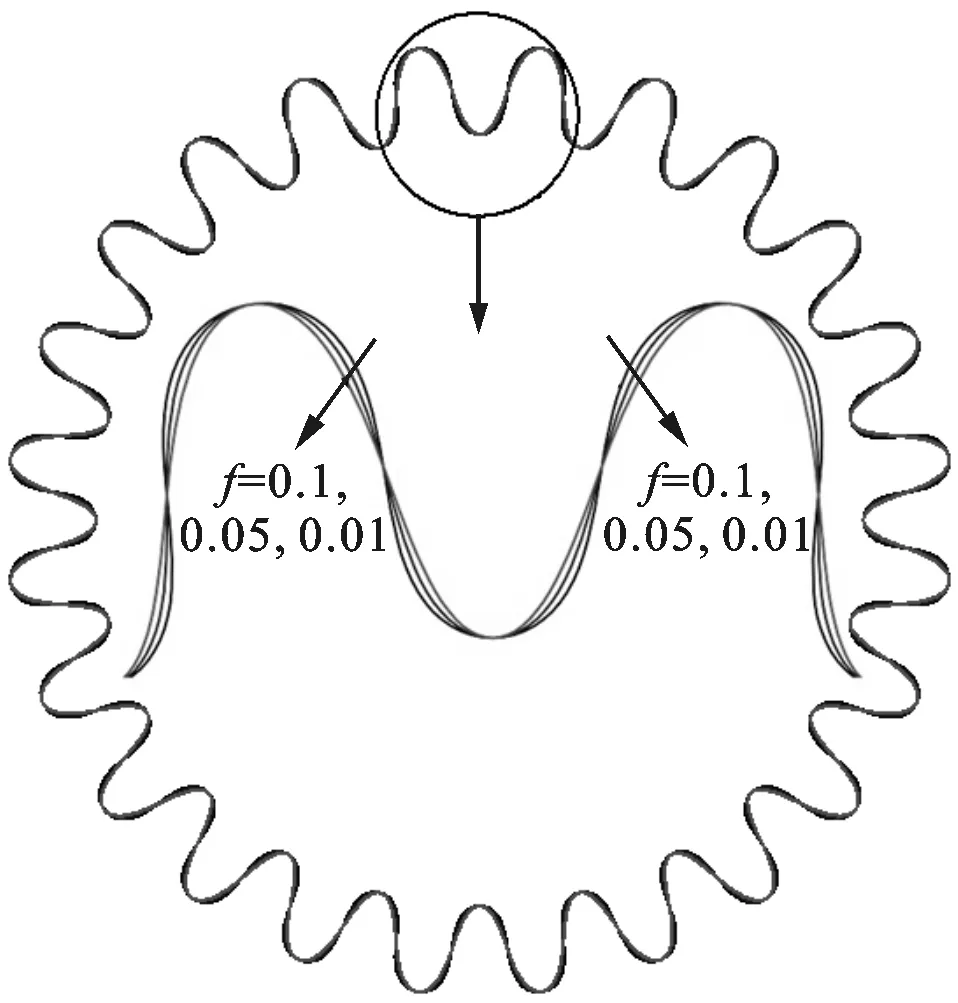
图4 齿形调控系数f1对四阶复合摆线齿形的影响

1.4 n阶复合摆线

综上所述,本文选择四阶复合摆线(下文简称复合摆线)作为齿廓曲线,建立复合摆线齿廓曲线外啮合共轭传动理论,并开展其传动特性方面的研究。

2 复合摆线外啮合齿轮副共轭原理

2.1 坐标系及坐标变换

以四阶复合摆线齿廓外啮合传动为研究对象,采用运动学法求解复合摆线的共轭齿廓,利用右手法则建立图5所示的坐标系。其中,固定坐标系Sf1(of1xf1yf1zf1)、Sf2(of2xf2yf2zf2)分别与箱体固联,动坐标系S1(o1x1y1z1)、S2(o2x2y2z2)分别与主动齿轮1、从动齿轮2固联,zf1轴、z1轴和zf2轴、z2轴分别与齿轮1、齿轮2的旋转轴重合,固定坐标系Sml(omlxmlymlzml)的原点oml与节点P重合,xf2轴平行于xf1轴,坐标系S1到坐标系S2、Sml的坐标变换矩阵分别为M21、M01。

齿轮1、2的中心距为a,传动比为i21,齿数分别为z1、z2,节圆半径分别为r1、r2,并且与分度圆重合,角速度分别为ω1、ω2,方向如图5所示。在初始位置,坐标系S1和Sf1重合、S2和Sf2重合,齿轮1、2分别以角速度ω1和ω2绕z1轴、z2轴运动一段时间t后,转过的角度分别为φ1、φ2。根据传动比的定义,可得到关系式

(12)

图5 平行轴外啮合共轭传动坐标系

对式(5)进行和差化积化简,可得到四阶复合摆线齿廓曲线Σ1在坐标系S1中的表达式

(13)

式中:r1(α)、α分别为齿廓曲线Σ1在坐标系S1中的矢径和角度参量。

根据共轭曲线啮合原理,啮合方程可表示为

(14)

f(α,φ1)=A1cos(α+φ1)+B1sin(α+φ1)+C1=0

(15)

式中

A1=r1[r1-2c1cos(z1α)+4f1c1z1cos(2z1α)]

B1=2c1r1[z1-2f1cos(z1α)]sin(z1α)

C1=2c1z1[-r1sin(z1α)+c1sin(2z1α)-

2.2 共轭齿廓方程

利用坐标变换矩阵M21和啮合方程(15),可求得复合摆线共轭齿廓Σ2在坐标系S2中的表达式

(16)

式中:r2(α,φ1)为共轭齿廓曲线Σ2在坐标系S2中的矢径,其通用表达式为

(17)

其中D1=sin[α+(1+i21)φ1],D2=cos[α+(1+i21)φ1],D3=2f1c1sin(2z1α),D4=r1-2c1cos(z1α)。

2.3 啮合线方程

将理论接触点在动坐标系中的坐标值转换到固定坐标系,即可得到齿轮副的啮合线方程。利用坐标变换矩阵M01,可得到复合摆线齿廓共轭传动的啮合线Σml的矢径rml(α,φ1)在坐标系Sml中的表达式

rml(α,φ1)=M01(φ1)r1(α,φ1)=

(18)

根据式(17)中的待定系数D3、D4,可推导得到啮合线方程的通用表达式

(19)

3 啮合特性分析

3.1 压力角

3.1.1 任意啮合点的压力角 压力角是衡量齿轮副传力性能好坏的重要参数,影响齿轮的几何尺寸、受力情况和传动强度。压力角定义为齿廓上某点的法向与线速度方向的夹角(取锐角)。如图6所示,复合摆线齿廓曲线Σ1与共轭齿廓曲线Σ2在点G啮合,点G对应的角度参量为αg,在齿廓曲线Σ1上点G的速度vg1与正压力F所在直线的夹角αg1,即为齿轮1的任意啮合点压力角[13],其表达式为

(20)

式中:Kv为vg1所在直线的斜率,Kv=-x1(αg)/y1(αg);Kn为正压力F所在直线的斜率,Kn=-dx1(αg)/dy1(αg)。

图6 复合摆线共轭传动齿轮副的压力角

对于图6中的三角形o1o2G,根据余弦定理可得到直线o1G和o2G的夹角

(21)

根据图6中αg1、αg2和ξ的几何关系,可得到共轭齿廓曲线Σ2在啮合点G处的压力角

αg2=|ξ+αg1-π|

(22)

3.1.2 分度圆压力角 若G点在Σ1的分度圆上,则可得到几何关系

(23)

由式(8)(9)(13)(20)(21)和(23),可求得Σ1在分度圆上的压力角

(24)

当齿轮副中心距为标准中心距时,节圆和分度圆重合,当啮合点G位于中心距连线上,即G点与节点P重合时,可得到几何关系

rg1+rg2=a

(25)

由式(9)(22)(24)和(25),可推导出Σ2的分度圆压力角

(26)

(27)

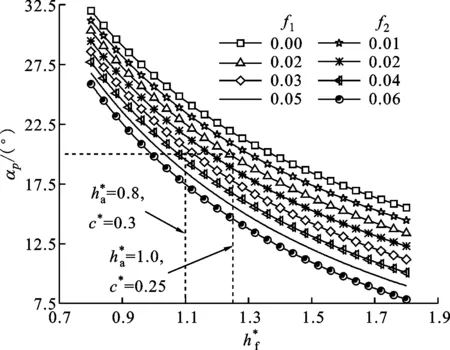
图7 齿根高系数对压力角的影响

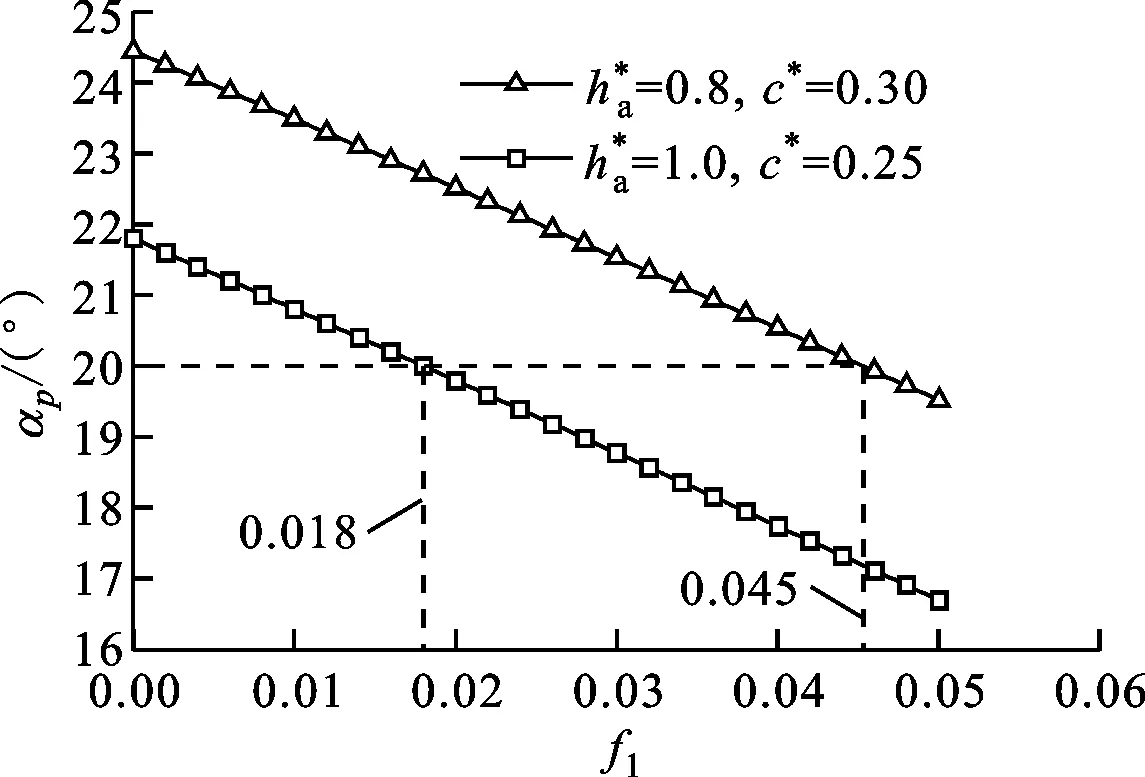
图8 齿形调控系数对压力角的影响

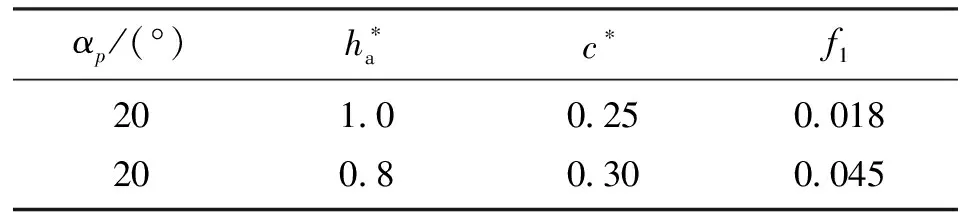
表2 齿形参数

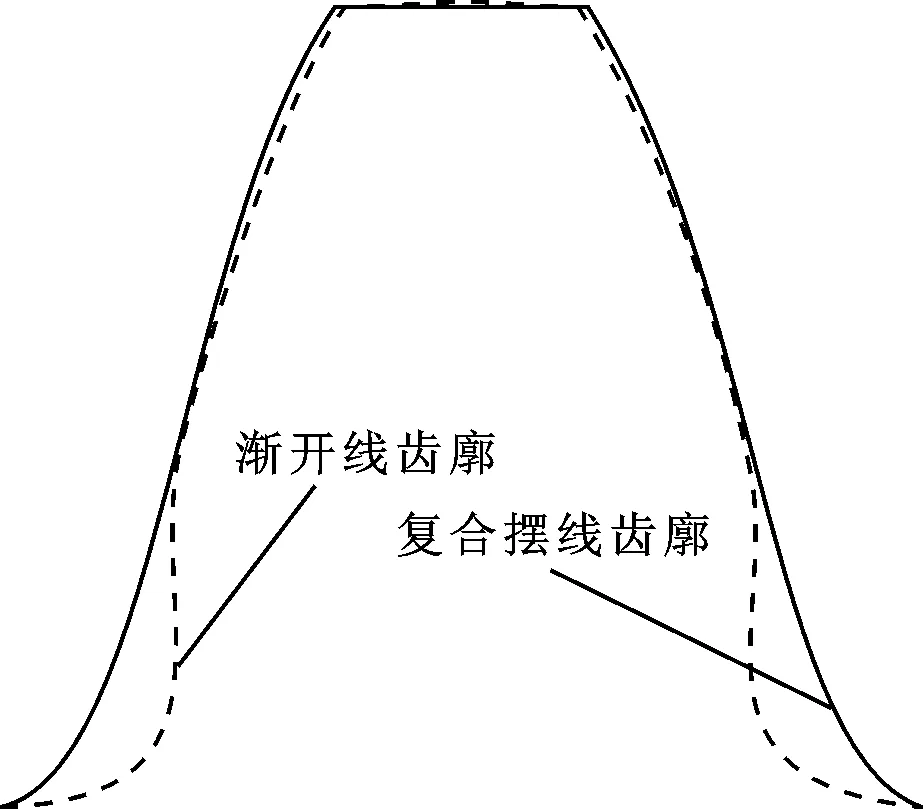
图9 复合摆线齿形设计

3.2 曲率

3.2.1 曲率模型 齿廓曲率模型是评价齿轮传动接触强度的基础,也是齿轮强度计算标准的重要组成部分。如图10所示,复合摆线齿廓Σ1与其共轭齿廓Σ2上任一啮合点Q(其角度参量为αv)的曲率分别用k1和k2表示。根据微分几何,可得到k1的表达式

(28)

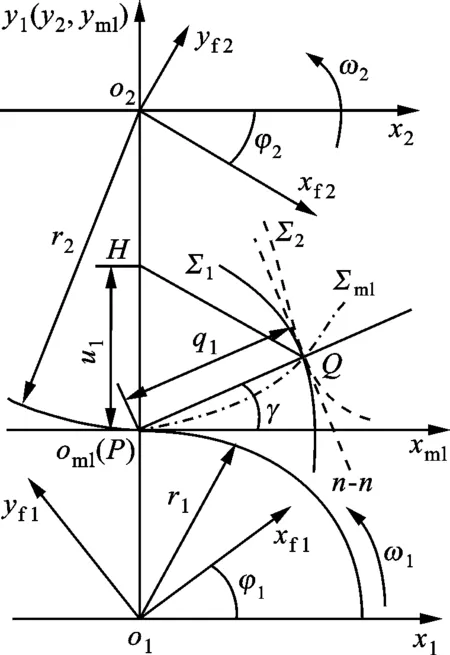
图10 共轭齿廓的几何曲率关系

根据式(13)(28),可化简得到曲率k1的表达式

(29)

式中:u1为H到节点P的距离,H为啮合点Q所在啮合线处的法线与y1轴的交点;q1为啮合点Q到节点P的距离。u1、q1的表达式为

(30)

(31)

根据Euler-Savary公式[14],得到共轭齿廓曲线曲率k1和k2的关系如下

(32)

由式(29)～式(32),可推导出Σ2的曲率

(33)

联立式(29)(30)(31)(33),可求得k1和k2。

(1)复合摆线齿廓Σ1及共轭齿廓Σ2都存在曲率为0的点,该点是曲线的拐点,也是曲线凹凸性的分界点,即齿廓Σ1、Σ2均由凸弧和凹弧组成,且传动过程始终为凹凸齿廓接触,有利于提高接触疲劳强度。同时,节圆附近的曲率极小,且变化梯度较小,有利于提高传动的承载能力和平稳性。

(2)复合摆线齿廓曲率很小,且随着齿形调控系数的减小,齿廓Σ1、Σ2的曲率差也相应减小,所以当齿高参数确定时,宜选取较小的齿形调控系数。

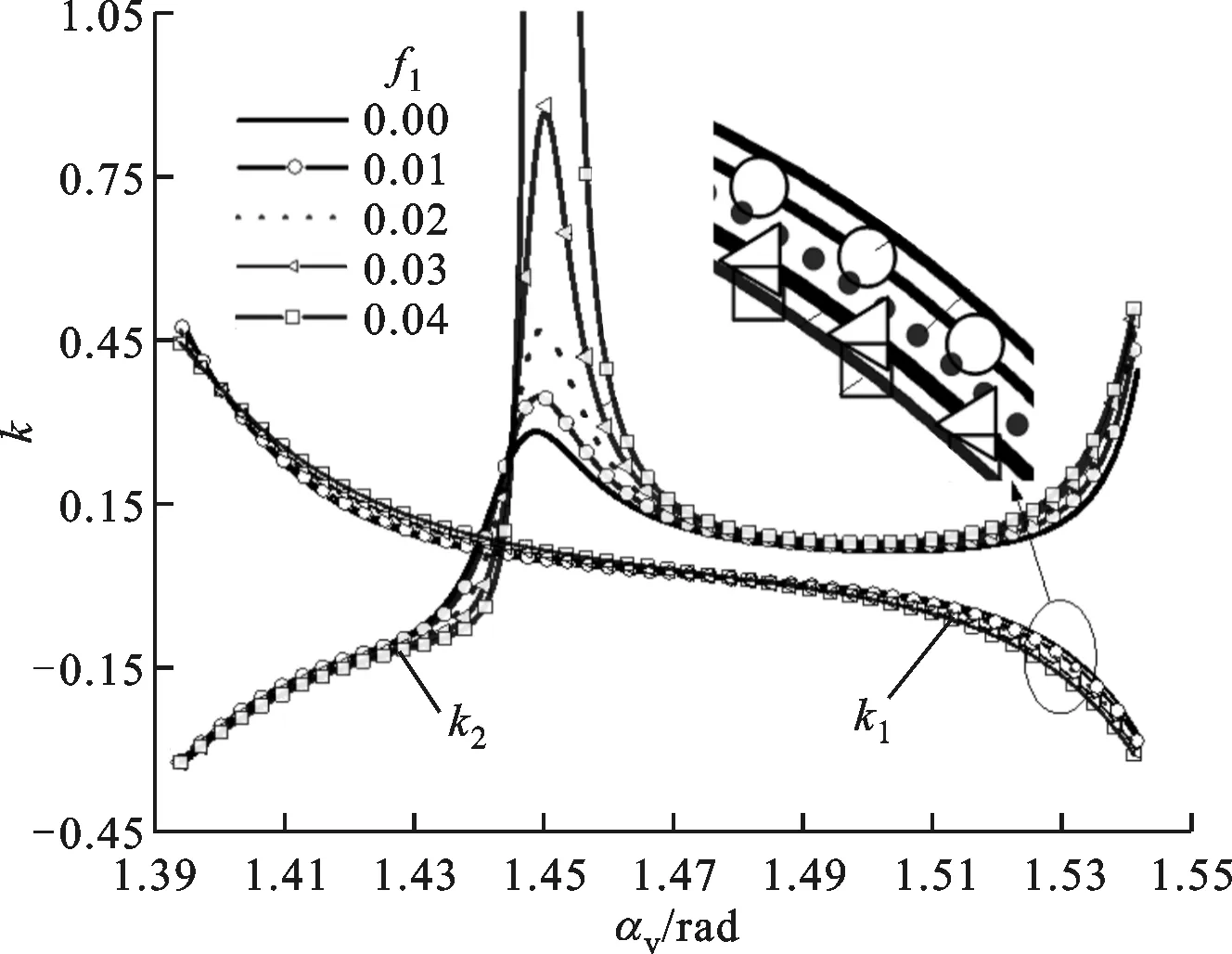
图时f1对齿廓曲率的影响

图时f1对齿廓曲率的影响

3.3 重合度

3.3.1 重合度模型 重合度是衡量齿轮副传动连续性、载荷传递均匀性的重要度量指标。如图13所示,曲线M2N2为复合摆线主动齿轮1的工作齿廓Σ1,齿轮2的齿廓Σ2是Σ1的共轭齿廓,曲线M1M2为复合摆线共轭传动的啮合线Σml,点M1是Σml与齿轮1齿顶圆的交点,点M2是Σml与齿轮2齿顶圆的交点,点M1、M2对应的角度参量分别为φa、φb。当啮合点M从M2移动到M1时,主动轮转过的角度Δα=αa-αb,则新型复合摆线齿轮副的重合度

(34)

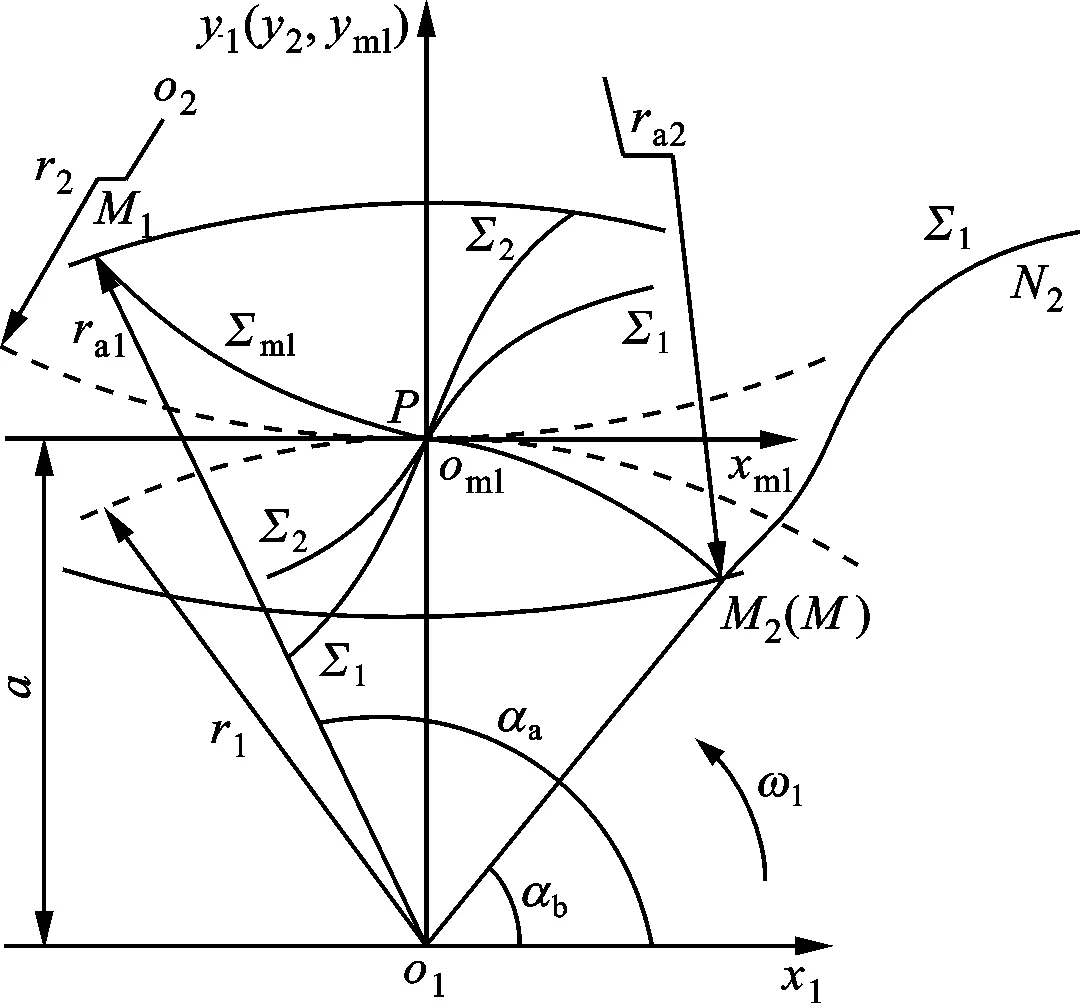
图13 复合摆线齿轮副重合度的几何关系

根据几何关系o1oml+omlM0=o1M0,可得

yml(αa)+r1=ra1sin(π-αa)

(35)

对于三角形o1M1o2,由余弦定理可得

(36)

由方程(35)(36)可分别求得φa、φb,然后代入方程(34)可求得重合度。

表3 齿轮副的重合度

由表3中的算例结果可知,复合摆线齿轮副的重合度明显大于传统渐开线齿轮的重合度,理论上具有更高的传动平稳性和载荷承载能力。

3.4 滑动率

3.4.1 滑动率模型 齿廓间较大的相对滑动易产生齿面磨损、胶合,增加功率损耗。为了提高齿轮传动性能,必须尽可能地减少齿面间的相对滑动。如图14所示,复合摆线齿廓Σ1及其共轭齿廓Σ2在某个瞬时啮合于W点(其角度参量为αs),经过时间Δt后,Σ1上的W1点与Σ2上的W2点啮合,此时啮合点W在Σ1、Σ2上走过的弧长分别为Δs1、Δs2,滑动弧长为Δs2-Δs1,则Σ1、Σ2在啮合点W的滑动率σ1、σ2[15]分别为

(37)

(38)

图14 滑动率几何模型

由啮合方程(15)、啮合线方程(19)可推导出滑动率的通用表达式

(39)

(40)

式中

其中∂αxml(αs,φ1)、∂φ1xml(αs,φ1)、∂αyml(αs,φ1)和∂φ1yml(αs,φ1)是啮合线方程(19)的偏导表达式,根据啮合方程(15)可求得φ1与αs的关系φ1=g(αs)。

3.4.2 滑动率分析 选取齿轮参数:m=3mm,z1/z2=32/73,zp=20°。利用数值软件MATLAB计算出2种齿高齿制下复合摆线齿轮副的滑动率,如图15所示。图16、图17是根据文献[15]求得的同参数渐开线齿轮副的滑动率随实际啮合线位置q1的变化曲线。

图15 复合摆线齿轮副的滑动率

从图15可以看出,复合摆线齿轮在整个啮合传动过程中,最大滑动率出现在轮齿啮入和啮出时的齿根位置,滑动率绝对值的最大值低于0.1,在节点附近趋近于0。与图16、图17所示的渐开线齿轮副的滑动率相比,复合摆线齿轮副的滑动率下降了近9/10,且在啮合极限点处滑动率仍极小,故在相同载荷下齿面磨损较小,有利于提高传动效率。

图时渐开线齿轮副的滑动率

图时渐开线齿轮副的滑动率

4 齿轮副实体模型构建与强度特性分析

4.1 齿轮副实体模型构建

根据FZG齿轮试验机的参数要求,设计出复合摆线齿轮副的基本参数,如表4所示。利用数值软件MATLAB计算出齿轮副的齿廓曲线数据,并导入三维建模软件SolidWorks,创建出精确的三维实体模型,如图18所示。同时,在SolidWorks中进行啮合仿真,结果显示复合摆线齿轮副在传动过程中能够实现连续线接触传动,且无啮合干涉现象。齿轮副实体模型的成功建立充分说明,新型复合摆线共轭传动理论与方法是可行的。

表4 复合摆线齿轮副的基本设计参数

图18 复合摆线齿轮副实体模型

4.2 强度特性分析

由于复合摆线齿廓的几何特殊性,利用解析法很难求得精确的弯曲应力和接触应力,而有限元法对齿廓形状没有限制,有着解析法不具备的优点,可以更精确、方便地分析复合摆线齿轮的强度特性,非常适用于非标准齿形的齿轮[16]。采用4.1节中的建模方法,选取和渐开线齿轮相同的参数:材料选用40Cr,弹性模量E=209GPa,泊松比ν=0.29;模数m=4mm,压力角αp=20°,齿数z1/z2=16/24,齿宽b=12mm。小齿轮输入转速和扭矩分别为1 000r/min、60N·m。利用有限元法求解复合摆线齿轮副的弯曲和接触应力,结果如图19、图20所示。

(a)复合摆线齿轮

(b)渐开线齿轮图19 齿根的弯曲应力云图

(a)复合摆线齿轮 (b)渐开线齿轮图20 齿面的接触应力云图

从图19可以看出,渐开线齿轮齿根的最大压应力、最大拉应力分别为129.22和121.05MPa,而相同负载下的复合摆线齿轮齿根的最大压应力、最大拉应力分别为95.166和84.731MPa,分别下降了26.35%和30.00%,即在相同模数下,采用复合摆线齿轮传动副可以提高齿轮的弯曲强度,有利于减小齿轮的尺寸和质量,提高齿轮的刚度。

从图20可以看出,齿面接触应力沿齿宽均匀分布,复合摆线齿轮、渐开线齿轮的齿面接触应力分别为721.50和922.99MPa,即在相同模数下,复合摆线齿轮的接触应力下降了21.83%,因此采用复合摆线齿轮传动可以有效提高齿面的接触强度。

5 齿轮副样件加工及传动效率试验

为了进行复合摆线齿轮副的传动试验评价,根据FZG齿轮试验机的参数要求,采用第4节中设计的复合摆线齿轮副参数(见表4),利用电火花慢走丝加工出复合摆线齿轮副试验样件,并进行了传动效率测试,同时,对FZG试验机配套的渐开线齿轮副也进行了传动效率测试,试验结果如图21所示。该渐开线齿轮副与复合摆线齿轮副具有相同的齿数、模数、压力角、齿顶高系数和顶隙系数。在传动效率测试过程中,复合摆线齿轮副传动平稳,运转良好。当小齿轮端加载扭矩为T1时,相应地可测出电机转速(大齿轮转速)在2 000、3 000和4 000r/min时大齿轮端的扭矩T2。T1、T2由扭矩传感器测量,并在试验机的在线监测测量系统上显示。齿轮副传动效率η的计算公式为

(41)

齿轮副的传动效率随加载扭矩的变化曲线见图21。

图21 复合摆线和渐开线齿轮副的传动效率曲线

从图21可以看出,复合摆线齿轮副的传动效率随加载扭矩在97.30%～99.00%的范围内呈正相关变化,且高于同工况下的渐开线齿轮副,可见其传动效率较高,具有工程应用价值。同时,尽管复合摆线齿轮样件为慢走丝线切割加工且未进行磨齿处理,齿轮精度不太高,而渐开线齿轮为精磨齿轮,齿轮精度相对较高(5级),但是即使在加工精度处于劣势的情况下,复合摆线齿轮副样件的传动效率仍高于渐开线齿轮副的传动效率,如果后期采用滚齿、精磨等适合批量生产的高精度加工方法,会进一步提高传动效率。

6 结 论

本文提出了广义摆线成形轨迹的二连杆等效机构转化方法,推导了n+1连杆机构的广义n阶摆线运动规律,提出了可用于齿轮传动的新型四阶复合摆线齿廓曲线构建方法;进一步推导出了复合摆线共轭齿廓曲线及啮合线的通用表达式,研究了复合摆线齿轮副的压力角、曲率、重合度、滑动率等啮合特性;建立了精确的复合摆线齿轮副三维实体模型,并加工了齿轮副试验样件,利用FZG齿轮试验机测得了齿轮副在不同工况下的传动效率。本文的研究获得以下结论。

(1)复合摆线齿轮副的压力角只与齿根高系数和齿形调控系数有关,当齿根高系数确定(即齿高确定)时,压力角随齿形调节系数的增大而减小,即在同一齿高下可有不同的压力角设计。

(2)相对于渐开线齿轮,复合摆线齿轮传动具有以下优势:传动过程始终为凹凸接触,有利于降低接触应力;重合度较大,传动平稳性和载荷承载能力较好;滑动率下降了近9/10,有利于减轻齿面磨损;齿根弯曲强度和齿面接触强度更高。

(3)复合摆线齿轮副的传动效率高于同工况下渐开线齿轮副的传动效率,具有工程应用价值。

后续将开展复合摆线齿轮滚切、插削和磨削等加工制造方法的研究,利用FZG齿轮试验机评价复合摆线齿轮传动的疲劳特性,以期为新型复合摆线齿轮传动奠定应用基础。

[1] 秦大同. 国际齿轮传动研究现状 [J]. 重庆大学学报(自然科学版), 2014, 37(8): 1-10. QIN Datong. Review of research on international gear transmissions [J]. Journal of Chongqing University (Natural Science Edition), 2014, 37(8): 1-10.

[2] CHEN Bingkui, ZHONG Hui, LIU Jingya, et al. Generation and investigation of a new cycloid drive with double contact [J]. Mechanism and Machine Theory, 2012, 49(4): 270-283.

[3] LI S. Design and strength analysis methods of the trochoidal gear reducers [J]. Mechanism and Machine Theory, 2014, 81(11): 140-154.

[4] HSIEH C F. Traditional versus improved designs for cycloidal speed reducers with a small tooth difference: the effect on dynamics [J]. Mechanism and Machine Theory, 2015, 87(4): 15-35.

[5] HSIEH C F. A new curve for application to the rotor profile of rotary lobe pumps [J]. Mechanism and Machine Theory, 2015, 87(5): 70-81.

[6] LITVIN F L, FUENTES A. Gear geometry and applied theory [M]. Cambridge, UK: Cambridge University Press, 2004: 358-360.

[8] GAMEZ-MONTERO P J, CASTILLA R, KHAMASHTA M, et al. Contact problems of a trochoidal-gear pump [J]. International Journal of Mechanical Sciences, 2006, 48(12): 1471-1480.

[9] 李远庆. 准纯滚动啮合的泛摆线齿轮传动 [J]. 机械传动, 2010, 34(11): 6-15 LI Yuanqing. Universal cycloid gear of prospective pure rolling meshing transmission [J]. Journal of Mechanical Transmission, 2010, 34(11): 6-15.

[10]陈焕. 新型摆线齿轮3K型减速器的设计研究 [D]. 哈尔滨: 哈尔滨工业大学, 2012: 10-42.

[11]薛云娜, 王勇, 王宪伦. 新型摆线传动的共轭啮合机理 [J]. 山东大学学报(工学版), 2005, 35(4): 26-29. XUE Yunna, WANG Yong, WANG Xianlun. Conjugate meshing mechanism of cycloid drive [J]. Journal of Shandong University (Engineering Science), 2005, 35(4): 26-29.

[12]郑州工学院机械原理及机械零件教研室. 摆线针轮行星传动 [M]. 北京: 科学出版社, 1978: 12-18.

[13]刘令涛, 焦永和, 张春林, 等. 内平动全摆线齿轮压力角的分析 [J]. 北京理工大学学报, 2010, 30(2): 158-160. LIU Lingtao, JIAO Yonghe, ZHANG Chunlin, et al. Pressure angle of internal parallel moving gears with whole cycloidal profiles [J]. Transactions of Beijing Institute of Technology, 2010, 30(2): 158-157.

[14]吴序堂. 齿轮啮合原理 [M]. 2版. 北京: 机械工业出版社, 2009: 42-49.

[15]陈兵奎, 梁栋, 彭帅, 等. 共轭曲线齿轮啮合管齿面的几何及接触特性分析 [J]. 西安交通大学学报, 2015, 49(3): 85-94. CHEN Bingkui, LIANG Dong, PENG Shuai, et al. Analysis on geometric and contact characteristics of tubular meshing tooth surfaces for conjugate-curve gears [J]. Journal of Xi’an Jiaotong University, 2015, 49(3): 85-94.

[16]肖望强, 李威, 韩建友, 等. 双压力角非对称齿轮传动接触分析 [J]. 北京科技大学学报, 2006, 28(12): 1167-1173. XIAO Wangqiang, LI Wei, HAN Jianyou, et al. Transmission contact analysis of the unsymmetric gear with double pressure angles [J]. Journal of University of Science and Technology Beijing, 2006, 28(12): 1167-1173.

(编辑 葛赵青)

Analysis on Transmission Characteristics of Novel Composite Cycloid Cylindrical Gears for External Driving

HAN Zhenhua,SHI Wankai,XIAO Yangyi,XU Lang

(State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030, China)

Based on the generation principle of traditional cycloid curves, a transforming method from cycloid curve generation to two-link equivalent mechanism is proposed, andnth-order cycloid motion is generalized usingn+1 link mechanism. Then the novel fourth-order composite cycloid equation for gear driving is derived. Based on differential geometry and conjugate engagement theory, conjugate profile equation of composite cycloid tooth profile curve is deduced. The pressure angle, curvature, contact ratio and sliding ratio of the composite cycloid gear driving are discussed. The composite cycloid gears are modeled accurately, and the strength characteristic of this drive is evaluated by FEM method simultaneously. The pressure angle of reference circle is controlled by the regulation coefficient of tooth profile when the tooth height is determined. The profile curve is formed smoothly by concave and convex arcs, and the concave-convex tooth surface is engaged by line contact in driving process, resulting in high contact fatigue strength. Compared with involute gear, a superior contact ratio and an incredibly small sliding ratio are demonstrated in composite cycloid tooth profile, and greater tooth root bending strength and surface contact strength are present in finite element method. In addition, experimental gear samples are machined, and its transmission efficiencies under different operating conditions are measured with FZG gear testing machine. The testing results show that the transmission efficiencies of the composite cycloid gears in the range of 97.30% to 99.00% are positively correlated with the loading torque. Importantly, they are higher compared with the involute gears under the same operating conditions. It is concluded that the composite cycloid gears show a remarkable engineering application value.

composite cycloid gear; gear drive; engaging principle; transmission characteristics

2016-03-25。 作者简介:韩振华(1986—),男,博士生;石万凯(通信作者),男,教授,博士生导师。 基金项目:国家重点基础研究发展计划资助项目(2014CB046304);国家自然科学基金资助项目(51675061)。

时间:2016-06-11

10.7652/xjtuxb201609002

TH132

A

0253-987X(2016)09-0010-10

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160611.1358.002.html