带有耗散项的KdV-BO方程解的适定性研究
2016-12-22孙海霞王虎生
孙海霞,王虎生,杨 晗,马 宇
(西南交通大学数学学院,四川 成都 611756)
带有耗散项的KdV-BO方程解的适定性研究
孙海霞,王虎生,杨 晗,马 宇
(西南交通大学数学学院,四川 成都 611756)
研究带有一般耗散项的KdV-BO方程的柯西问题.KdV-BO方程是描述长波在深槽双流体系统中传播的模型,该流体系统中的低层流体是具有很大密度,交界面处有毛细现象.首先,本文借助半群和压缩映像原理得到了方程柯西问题的局部适定性.其次,基于能量积分估计,对满足一定条件的耗散项,得到方程的整体适定性,最后,文章研究了方程解的指数衰减性.
KdV-BO方程;耗散项;适定性;衰减性
1 引言
本文研究带有耗散项Lγ(u)的KdV-BO方程的柯西问题
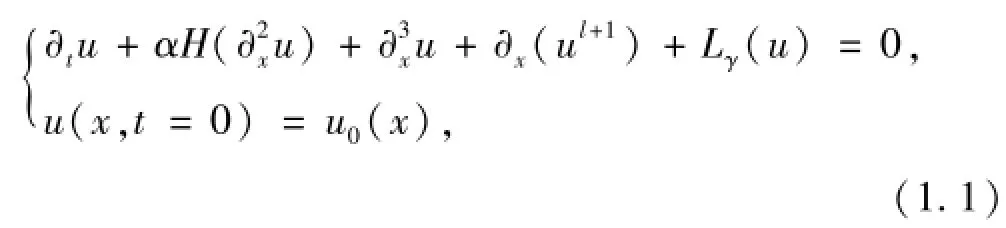
其中阻尼算子Lγ(u)是由如下的傅里叶变换算子给定
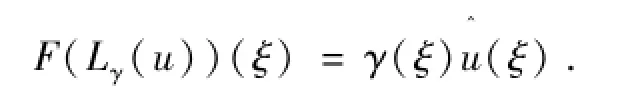
这里γ(ξ)>0,ξ∈R,且满足如下性质
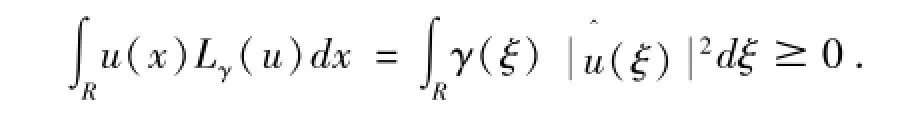
首先我们来回顾经典的KdV-BO方程的柯西问题
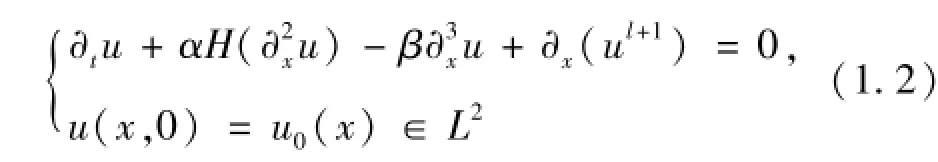
的已有研究结果,其中α,β为常数,且满足αβ≠0,H为Hilbert变换,即
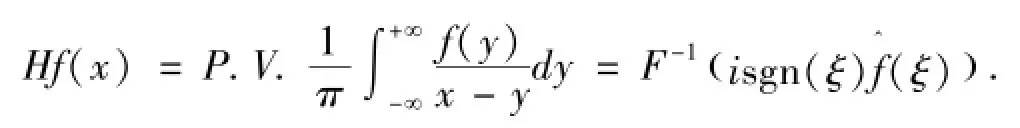
方程(1.2)是描述长波在深槽双流体系统中传播的模型,该流体系统中的低层流体是具有很大密度,交界面处有毛细现象.KdV-BO方程中既包含KdV方程的成分,又包含BO方程的成分,这两种方程有许多类似的性质,例如N-孤子解,Baclund变换与Lax对以及无穷多个守恒律等(参见文献[10]).
事实上,当α=0时,(1.2)描述的是长波在浅水中的传播,(1.2)则变为著名的KdV方程.KdV方程模型是在研究小振幅长波单向传播时得到的(文献[1]),记为
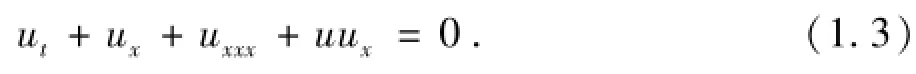
对于(1.3)有许多的研究,例如在文献[2]中,Bona等人研究了KdV方程的周期初边值问题
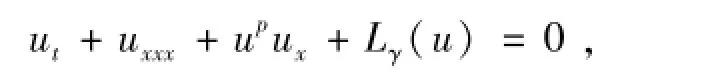
并研究了耗散项Lγ(u)对解的整体适定性的影响.事实上他们研究了Lγ(u)为 -δuxx与σu两个耗散项时的情形,并得出当p≥4时,存在临界值δc和σc使得当δ>δc或σ>σc时,整体解是存在的.
文献[3]中作者考虑了更一般的耗散项Lγ(u),并研究了带有耗散项的KdV方程
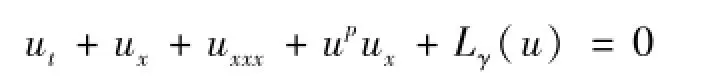
解的适定性问题,得到当 p<4时,整体解在H1(R)中存在,p≥4时,整体解在H2(R)中存在.
当β=0时描述的是长波在深水中的传播,即是BO方程.文献[4]中,Ponce证明了BO方程
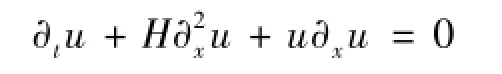
关于研究KdV-BO方程的解的存在性,稳定性及其孤波解有很多文章研究过,例如文献[6],[7].文献[8]研究了如下柯西问题
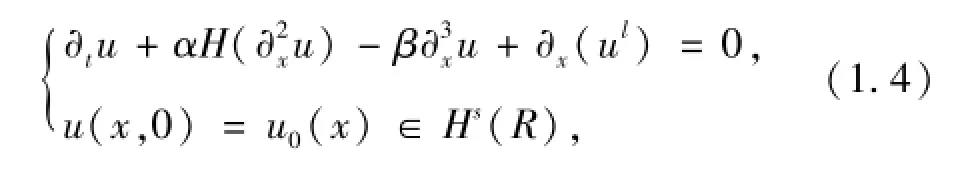
在本文中,我们考虑(1.4)带有耗散项Lγ(u)的情形,即研究了柯西问题(1.1)的解的适定性,同时在给定Lγ(u)条件下研究解的整体适定性,作为附加产品,也研究了方程解的L2范数的指数衰减性.
下面给出一些记号:空间Hγs(R)定义为
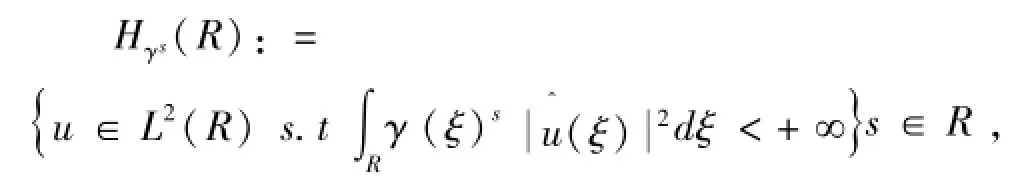
其空间范数为
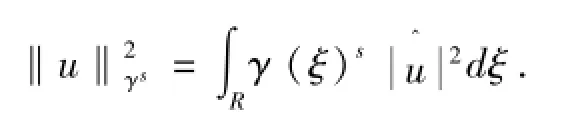
2 预备知识
本节给出耗散项、空间和线性半群的一些性质,将在后面用到.
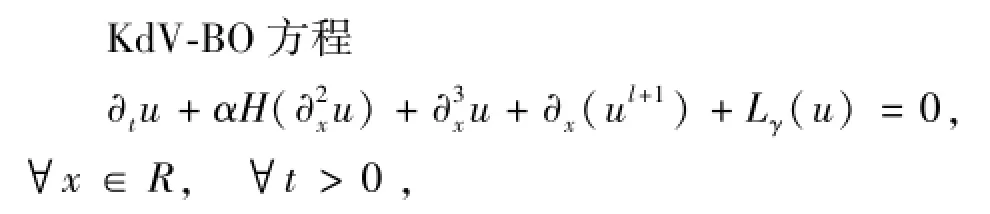
其线性部分生成的半群可以表示为
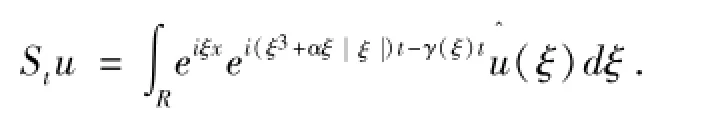
在后面的部分,将f(u)定义为方程的非线性项,即f(u)=∂x(ul+1).
引理2.1 假定s,r∈R+,存在一个仅依赖于r的一个常数Cr>0使得对∀u∈Hγs(R)和∀t>0,我们有

下面给出关于空间Hγs(R)中嵌入的一些结论及KdV-BO方程中算子的一些性质.
引理2.3 设γ和β使的对所有的ξ∈R有γ(ξ) >β(ξ).定义
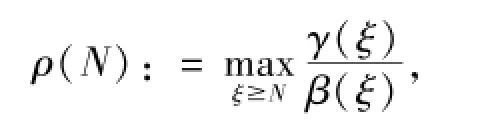
Hγ(R)到Hβ(R)的连续嵌入是紧的当且仅当
引理2.4 假设u,v∈Hγ(R)且存在一个常数C >0使得对∀ξ,η∈R我们有
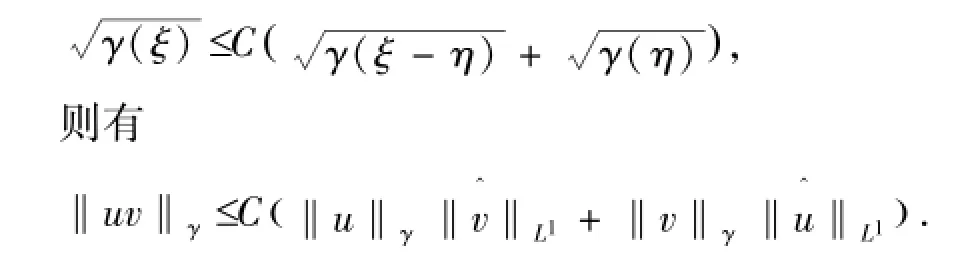
引理2.5 H为Hilbert变换,它具有下述的重要性质:
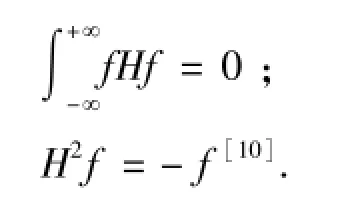
3 局部适定性
我们研究方程的柯西问题:∀x∈R,∀t>0,
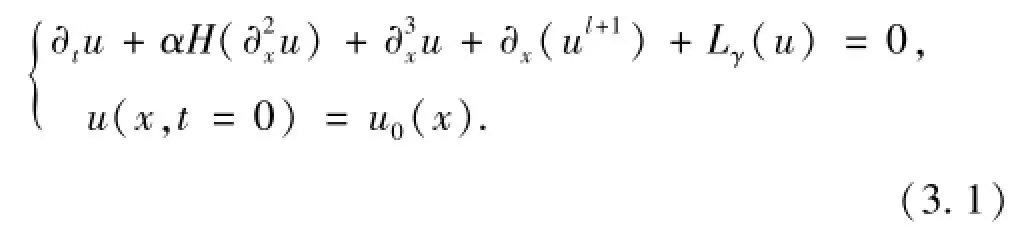
首先我们来陈述问题的适定性.
定理3.1 假设γ(ξ)满足以下条件
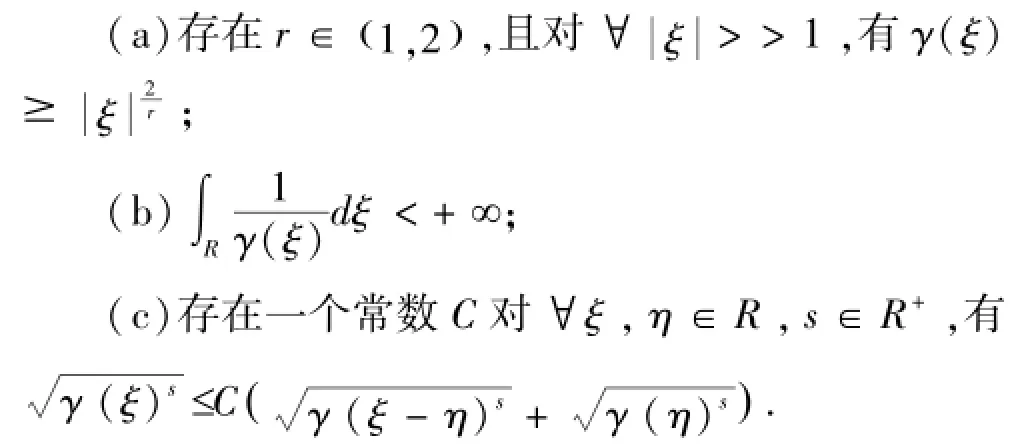
此外,对所有的M >0有‖u0‖γs≤M,‖v0‖γs≤M,存在常数C1>0使得方程与初值u0,v0有关联的解u,v满足对所有的有
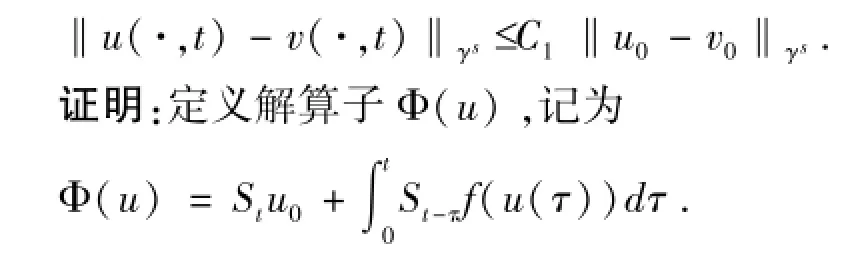
让来证明解的存在唯一性.对∀T>0定义 B (T)

由此容易得知空间B(T)是一个完备的度量空间.
应用皮卡不动点定理,首先来证明Φ(B(T))⊂B(T).取u∈B(T),我们有
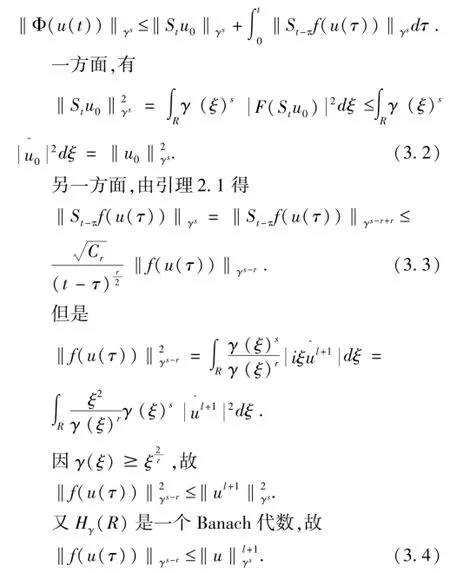
因此,由(3.2)、(3.3)和(3.4)式得:

现在来证明Φ是一个严格的压缩映射.令u,v ∈B(T),证明对∀t∈ 0,T[ ],


4 整体适定性
在前面引理假设的前提下,使用能量方法来研究KdV-BO方程的整体适定性.
定理4.1 当l<4时,对所有的γ,整体解在H1(R)中.否则(当l≥4时),存在常数θ>0使得当γ(ξ)≥θ,∀ξ∈R,整体解在H2(R)中.
证明:当l<4时,N(u)和E(u)是方程的不含耗散项的两个量,他们分别是L2范数和能量.其表达式为




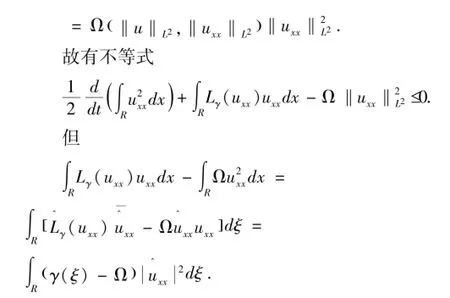
Ω是一个递增的函数,而‖u(·,t)‖L2关于t是递减的,则当t=0,γ(ξ)-Ω≥0时,‖uxx(·,t)‖L2关于t≥0不可能是递增的.
特别地,当γ(ξ)≥Ω (‖u0‖L2,‖u0xx‖L2)=:θ时,半范数‖uxx(·,t)‖L2在t=0下是有界的.
5 方程解的衰减性
定理5.1 KdV-BO方程具有L2范数守恒的性质,但加了耗散项Lγ(u)之后,L2范数指数衰减,即

证明:对方程
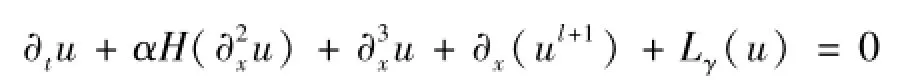
作能量积分.用u乘方程的两边,然后对x积分:
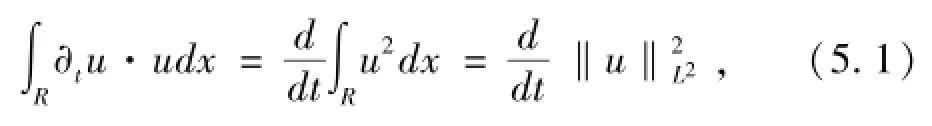

因此,对所有的t,方程解是L2范数指数衰减的.
[1]KORTEWEG D J,DE VRIES G.XLI.On the change of form of long waves ad-vancing in a rectangular canal,and on a new type of long stationary waves[J].Phi-losophical Magazine Series 5,1895,39(240): 422-443.
[2]BONA J L,DOUGALIS V A,KARAKASHIAN O A,et al.The effect of dissip-ation on solutions of the generalized Korteweg-de Vries equation [J].Journal of Computational and Applied Mathematics,1996,74(1-2):127-154.
[3]GAMIER P.Damping to prevent the blow-up of the Korteweg-de Vries equation[J],arXiv:1503.08559v1,2015-3.
[4]PONCE G.On the global well-posedness of the Benjami-Ono equation [J].Differential Integral Equations,1991,4:52-542.
[5]IORIO R J.On the cauchy problem for the benjami-ono equation[J]. Communications in Partial Differerential Equations,1986,11(10): 1031-1081.
[6]ANGULO J.Existence and stability of solitary wave solutions of the Benjamin eq-uation[J].Journal of Differential Equations,1999,152: 136-159.
[7]BENJAMIN T B.A new kind of solitary waves[J].Journal of Fluid Mechanics,1992,245:401-411.
[8]GUO B,HUO Z.The well-posedness of the Korteweg-de Vries-Benjamin-Ono equation[J].Journal of Mathematical Analysis and Applications,2004,295(2):444-458.
[9]LINARES F.L2global well-posedness of the initial value problem associated to the Benjamin equation[J].Journal of Differential Equations,1999,152(2):377-393.
[10]郭柏灵.非线性演化方程[M].上海:科技教育出版社,1995,9.
[11]AMICK C J,BONA J L,SCHONBEK M E.Decay of solutions of some nonline-ar wave equations[J].Journal of Differential Equations,1989,81(1):1-49.
[12]IORIO R J,KORTEWEG D J,BO,et al.In Functional analytic methods for part-ial differential equations[R].Berlin:Lecture Notes in Mathematics,1990.
[13]GUO B,TAN S.Long time behavior for the equation of finite-depth fluids[J].Communications in Mathematical Physics,1994,163(1):1-15.
[14]TAO T.Multilinear weighted convolution of L2functions,and applications to nonlinear dispersive equation[J].American Journal of Mathematics,2001,123:839-908.
[15]OTT E,SUDAN R N.Damping of solitaries waves[J].Physics of Fluids,1970,13(6):1432-1435.
(责任编辑:付强,张阳,李建忠,罗敏;英文编辑:周序林)
The well-posedness of KdV-BO equation with dissipation
SUN Hai-xia,WANG Hu-sheng,YANG Han,MA Yu
(Department of Mathematics,Southwest Jiaotong University,Chengdu 611756,P.R.C.)
This paper studies the Cauchy problem of the KdV-BO equation with dissipative term.The equation models are the undirectional propagation of long waves in a two-fluid system,where the lower fluid with greater density is infinitely deep and the interface is subject to capillarity.Firstly,the local well-posedness for the Cauchy problem is obtained by the contraction mamapping theorem.Secondly,based on the energy estimates,the global well-posedness for the equation with the dissipative term which satisfies certain conditions is received.Finally,the exponential decay of the solutions to the equation is proved.
KdV-BO equation;dissipation;well-posedness;decay
O175
A
2095-4271(2016)04-0446-06
10.11920/xnmdzk.2016.04.014
2015-11-16
孙海霞(1990-),女,汉族,山西人,硕士研究生,研究方向:偏微分方程,E-mail:1170537536@qq.com.
杨晗(1969-),男,汉族,教授,研究方向:非线性发展偏微分方程解的适定性.
国家自然科学基金项目(No.71572156).
