关于Hilbert空间中一类广义随机非线性变分不等式
2016-12-22周武
周 武
(西南民族大学计算机科学与技术学院,四川 成都 610041)
关于Hilbert空间中一类广义随机非线性变分不等式
周 武
(西南民族大学计算机科学与技术学院,四川 成都 610041)
介绍并研究了Hilbert空间中的Minty型广义随机非线性变分不等式问题,并在适当的条件和假设下,得到了这类广义非线性随机变分不等式和Stampacchia型广义随机非线性变分不等式的等价的结论;运用该结论,结合随机化的Banach压缩映像原理得到了关于这一类广义随机非线性变分不等式问题的一些新的随机解的存在性结果.
随机变分不等式;随机算子;随机不动点;存在性
1 引言及预备知识
变分不等式的理论、方法与技巧,可以应用于控制论、最优化理论、数学规划等许多问题的研究.在一定条件下,经济金融中的均衡问题、交通网络中的运输问题、物理中的一部分流体力学问题都可以转化为某一形式的变分不等式问题来加以研究.由于现实世界中的许多问题都会涉及的非线性和不确定性问题的处理,从而对非线性和随机变分不等式的研究得到了许多作者的关注与研究[1-15].
本文的目的是研究一类Hilbert空间中的Minty型广义随机非线性变分不等式问题,并在适当的条件和假设下,得到了关于这类广义随机非线性变分不等式问题的一些新的随机解的存在性结果.
本文以下处处设(Ω,μ)是一可测空间.X是一可分的Hilbert空间,〈.,.〉,‖.‖非别表示X上的内积和范数;β(X)表示X中的Borel子集的σ-代数.
一个映像 u:Ω→X称为可测的,如果∀B∈β(X),集合 {ω∈Ω:u(ω)∈B}∈μ一个映像T:Ω×X→X称为随机的,如果对于任给的x∈X,ω→T(ω,x) =y(ω)是可测的.
定义1 设T:Ω×X→X是一个随机映像,称T 为
(1)单调的,如果∀x,y∈X,〈T(ω,x)-T(ω,y),xy〉≥0,ω∈Ω.
(2)T称为强单调的,如果存在一可测函数α:Ω ↦(0,∞),使得对任一ω∈Ω有〈T(ω,x)-T(ω,y),xy)〉≥α(ω)‖x-y‖2,∀x,y∈X;
(3)称T为Lipschity连续的,如果存在一可测函数β:Ω↦(0,∞),使得对一切ω∈Ω有
(4)T称为半连续的,如果映像λ→T(ω,λx+(1-λ)y):[0,1]→X对任给的序列{λn}⊂[0,1]
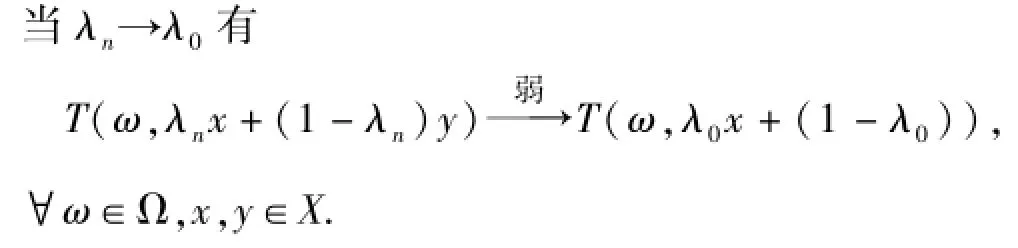
定义2 设K是X中的闭凸子集,S,T:Ω×X→X是两个随机算子.所谓的关于S和T的随机Minty型广义非线性变分不等式是求一可测映像x:Ω→K,使得
定义3 设K是X中的闭凸子集,S,T:Ω×X→X是两个随机算子,所谓的关于S和T的随机Stampacchia型广义非线性变分不等式是求一可测映像x:Ω →K,使得

引理1 设K是X中的闭凸子集,S,T:Ω×X→X是半连续的单调的随机映像,则下列结论等价:
(1)x:Ω→K是随机Minty型广义变分不等式(1.1)的随机解;
(2)x:Ω→K是随机Stampacchia型广义非线性变分不等式(1.2)的随机解;证明:(2)⇒(1)设x:Ω→K是随机Stampacchia型广义非线性变分不等式(1.2)的随机解,故有

即x:Ω→K是随机Minty型广义非线性变分不等

2 主要结果
定理1 设X是一实的可分的Hilbert空间,K是X中之一闭凸子集.T:Ω×K→X是一个强单调Lipschitz连续的随机算子,其相应的强单调系数和Lipschitz系数(均为可测函数)分别为

而S:Ω×K→X是一个Lipschitz连续的随机算子,其Lipschitz系数为可测函数γ:Ω→(0,∞),并且满足下述条件则随机Minty型广义非线性变分不等式(1.1)有唯一的随机解x∗:Ω→K.

证明:因为K是闭凸子集,由熟知的Hilbert空间中的极小化向量定理,对于每一y∈K和每一ω∈Ω存在唯一的x(ω)∈K,使得


由假定条件,随机算子T是α-强单调,并且是β-Lipschitz连续的,其中α,β:Ω→(0,∞)是两个可测函数,满足0<β2(ω)<2α(ω)-γ(ω),∀ω∈Ω.
而S是γ-Lipschitz连续的,于是由(2.5)可得

则θ:Ω→(0,1)是一可测函数,故由(2.6)知道
F:Ω×K→K是一随机的Banach压缩映像,由随机化的Bananch压缩定理知道(参见 7[]):F存在一随机不动点,即存在可测映像x∗:Ω→K,使得

故x∗:Ω→K是随机Stampacchia型广义非线性变分不等式(1.2)的随机解.
由引理1即知x∗:Ω→K是随机Minty型广义非线性变分不等式(1.1)的随机解.
定理1 易有下述结果:
定理2 设X是一实的可分的Hilbert空间,K是X中之一闭凸子集.T:Ω×K→X是一强单调的Lipschitz连续的随机算子,其相应的强单调系数和Lipschitz系数(均为可测函数)分别是α:Ω→(0,∞),β:Ω→[0,∞)并满足条件:0<β2(ω)<2α(ω),∀ω∈Ω则下述随机Minty型非线性变分不等式〈T(ω,y),y-x (ω)〉≥0,∀y∈K,ω∈Ω有唯一的随机解x∗:Ω→K.
[1]GANGULY A,WADHWA K.On random variational inequalities[J]. Mathematical Programming,1997,206:315-321.
[2]RICHARD W C,PANG J S,RICHARD E S.The Linear Complementarity Problem[M].London:Academic Press,1992.
[3]CRANK J.Free and Moving Boundary Problems[M].Oxford:Clarendon,1984.
[4]ISAAC G.Complementarity Problems[M].Lecture Notes in Math 1528,Berlin:Springer-Verlag,1993.
[5]HUANG N J.Random generalized nonlinear varational inclusions for random fuzzy mappings[J].Fuzzy Sets and Systems,1999,105:437-444.
[6]张石生.变分不等式和相补问题理论及应用[M].上海:上海科技出版社,1991.
[7]张石生.不动点理论及应用[M].重庆:重庆出版社,1984.
[8]CHEN X J,FUKUSHIMA M.Expected residual minimization method for stochastic linear complementarity problems[J].Mathematics of Operations Research,2005,30:1022-1038.
[9]CHEN X J,ROGER J B,ZHANG Y F.Stochastic variational inequalities:residual minimization smoothing sample average approximations [J].SIAM Journal of Optimization,2012,22:649-673.
[10]CHEN X J,ZHANG C,FUKUSHIMA M.Robust solution of monotone stochastic linear complementarity problems[J].Mathematical Programming,2009,117:51-80.
[11]LIN G H,FUKUSHIMA M.New reformulations for stochastic nonlinear compelementarity problems[J].Optimization Methods and Software,2006,21:551-564.
[12]JIANG H Y,XU H F.Stochastic approximation approaches to the stochastic variational inequality problems[J].IEEE Transaction on Automatic Control,2008,53:1462-1475.
[13]LUO M J,LIN G H.Expected residual minimization method for stochastic variational inequality problems[J].Journal of Optimization Theory and Applications,2009,140:103-116.
[14]TAN K K,YUAN G X Z.On deterministic and random fixed points [J].Proceedings of the American Mathematical Society,1993,119: 849-856.
[15]TAN K K,YUAN G X Z.Random fixed point theorems and approximation in cones[J].Journal of Mathematical Analysis and Applications,1994,185(2):378-390.
(责任编辑:付强,张阳,李建忠,罗敏;英文编辑:周序林)
A class of generalized random nonlinear variational inequalities in Hilbert spaces
ZHOU Wu
(School of Computer Science and Technology,Southwest University for Nationalities,Chengdu 610041,P.R.C.)
This paper introduces and studies generalized random nonlinear Minty variational inequalities in Hilbert spaces.Under some suitable conditions,the equivalent relationship is obtained between generalized random nonlinear Minty variational inequalities and generalized random nonlinear Stampacchia variational inequalities.Using the radom Banach fixed point theorem,some new results of random solutions for this class of random varational inequalities in the setting of Hilbert spaces are obtained.
random varational inequality;random operator;random fixed point;existence
O177.1
A
2095-4271(2016)04-0443-03
10.11920/xnmdzk.2016.04.013
2015-10-13
周武(1962-),男,汉族,四川人,副教授,研究方向:运筹学.
