城市路网的分布式鲁棒预测控制

刘安东，李 佳

(浙江工业大学 信息工程学院，浙江 杭州 310023)



城市路网的分布式鲁棒预测控制

刘安东，李 佳

(浙江工业大学 信息工程学院，浙江 杭州 310023)

针对具有模型不确定的城市路网系统，研究了使闭环系统渐近稳定的分布式鲁棒预测状态反馈控制器设计问题.首先，将由“存储与向前”路段线性模型扩展得到的城市路网拓扑模型分解为分布式模型.同时考虑实际情况中路况变化、测量误差等因素引起的饱和流量、车辆数的不确定性对城市路网系统的影响，得到了具有不确定参数的城市路网分布式模型.然后，提出了一种合作式的分布式鲁棒预测控制算法，并利用线性矩阵不等式(linear matrix inequality,LMI)处理方法在线求解多个凸优化问题，给出了子系统控制器求解方法.最后通过Matlab仿真验证了分布式鲁棒预测控制是一种能有效缓解城市交通拥堵和优化信号灯的控制策略.

分布式鲁棒预测控制；路网分布式模型；不确定性参数；线性矩阵不等式

近几十年来，随着车辆数的增加，交通拥堵已经成为阻碍社会经济发展的重要因素.在城市路网系统中，由于交通流的时段性及交通基础设施的不可扩展性，拥堵问题尤为严重[1-2].因此，迫切需要一种有效的控制策略来缓解城市交通拥堵和优化路口信号灯.在已有的控制策略中，实时控制策略具有对当前变化的交通状况做出及时调整的优点，从而比定时控制策略具有更广阔的发展前景[3].实时控制可分为基于实时交通流和基于状态空间模型的实时控制[4-5]，其中基于模型的控制方法能更好地运用现代控制理论方法，故近年来得到了较快地发展与应用，并成为当前的一个研究热点[6].实时控制可分为集中式控制、分散式控制和分布式控制.由于城市路网系统中含有大量耦合性较强的相邻路口，故分散式控制不能通过信号灯时间的调整来有效地协调路口之间的交通状况[7].集中式控制是目前城市路网系统中应用较广的控制策略：文献[8]中Diakaki等使用基于“存储与向前”路段模型的路网系统模型，采用LQR方法求解绿灯相位时间的反馈控制律，虽然该方法简单方便，但无法处理带有约束的最优化问题；模型预测控制是一种能有效处理约束的先进算法[9]，文献[10]中K. Aboudolas等基于改进的“存储与向前”非线性模型使用模型预测控制方法求解了带有约束的最优化问题，但是该非线性模型建模复杂，求解优化问题计算量大.虽然集中式控制方法算法简单，实施便捷，但是系统通信量大、故障率高，所以近年来学者们对分布式控制策略进行了研究：文献[11]中作者提出了一种基于多智能体的分布式交通信号控制方法，通过相邻路口信号控制智能体的信息交互和协调，使相邻路口驶来的车队不停车地通过路口；文献[12]中Eduardo Camponogara等使用DMPC(Ditributed model predictive control)解决了带有相位时间和车队长度约束的全局优化问题；文献[13]中X. Zhou等使用分布式控制策略解决了带有相位时间约束的合作式邻域优化问题.然而，以上文献采用的分布式模型均为精确模型，而实际情况中路况变化、测量误差等因素引起的饱和流量、车辆数的不确定性会导致“存储与向前”模型的参数不确定，因此基于精确模型的算法在具有不确定因素影响下无法获得很好的控制效果.

针对实际情况中路况变化、测量误差等因素引起的饱和流量、车辆数的不确定性所导致的“存储与向前”线性模型的参数不确定，笔者采用合作式的分布式鲁棒预测控制方法设计各子系统的状态反馈控制器用于调节子系统中路口的绿灯相位时间.首先将传统的“存储与向前”模型分解为分布式模型，同时考虑参数不确定性和绿灯时间约束，得到了带有参数不确定的路网系统分布式模型；然后提出一种合作式的分布式鲁棒预测控制算法，并利用LMI处理方法解决多个具有约束的凸优化问题，给出了子系统控制器的求解方法；最后，通过仿真验证鲁棒预测控制策略能通过协调各子系统中的路口信号灯的相位时间来有效缓解城市交通的拥堵状况.

1 城市路网系统建模

1.1 “存储与向前”模型

“存储与向前”路段模型由两个相邻路口(M，N)及连接两个路口的一条道路z组成，且z∈OM，z∈IN，其中，OM表示路口M的下游路段，IN表示路口N的上游路段，如图1所示.

图1 “存储与向前”路段模型Fig.1 “Store and forward” segment model

根据图1建立路段模型为

xz(k+1)=xz(k)+T[qz(k)-sz(k)+ dz(k)-uz(k)]

(1)

式中：T为采样周期；xz(k)为kT时刻路段z中的车辆数；qz(k)为[kT,(k+1)T)时间段内从上游路段通过路口M进入下游路段z的平均流量；sz(k)为[kT,(k+1)T)时间段内从路段z中途驶离的平均流量；dz(k)为[kT,(k+1)T)时间段内从路段z中途驶入的平均流量；uz(k)为[kT,(k+1)T)时间段内从上游路段z通过路口N进入下游路段的平均流量.其中：

(2)

X(k+1)=X(k)+BU(k)+d(k)

(3)

在实际交通系统中，每个相位时间必须大于最短绿灯时间且小于最长绿灯时间，故控制变量U(k)的约束条件为

uz,min≤uz(k)≤uz,max

(4)

式中uz,min，uz,max分别为路段z中车辆有权通过路口的最短、最长相位时间占信号周期的百分比，uz,min可以为零，表示相应的相位的绿灯时间为零，即出现全红相位.另外，路口j的各相位绿灯时间百分比之和应满足：

(5)

式中：Lj为路口j的黄灯时间之和；Cj为路口j的信号周期；Pj为路口j的相位数.

1.2 带有不确定的分布式模型

为了使得路网控制系统的控制效果达到一个稳态点，从而协调路网系统中的各路段的交通状况，首先给出定义为

ΔX=X-XN,ΔU=U-UN,Δd=d-dN

(6)

式中：XN为状态量X的稳态值，即各路段的期望车队长度；UN为系统达到稳定时的控制量；dN为d的统计意义上的平均值，由文献[14]知可以令Δd=0.由XN(k+1)=XN(k)得稳态系统为

XN(k)=XN(k)+BUN+dN

(7)

由式(7)可知：

BUN+dN=0

(8)

从而求解UN转化为求可行解问题：

(9)

结合式(3，7)可得集中式状态空间模型为

ΔX(k+1)=ΔX(k)+BΔU(k)

(10)

在分布式控制系统结构中，采用协调控制策略，考虑子系统控制器之间的通信，将式(10)中的控制变量ΔU(k)按路口进行分解，得到城市路网系统中子系统i(i=1,2,…,m)的模型：

在实际交通状况中，由于测量误差、饱和流量的浮动等多种外界因素对交通流量的影响，将会导致交通模型具有不确定性，为此引入不确定矩阵，则式(11)可以转换为

(12)

式中：ΔAi(k)ΔXi(k)为车辆数的测量误差；ΔBii(k)和ΔBij为饱和流量的浮动误差，且ΔAi，ΔBii，ΔBij满足：

(13)

ΔBii(k)=EbiiΔbi(k)Fbii,ΔBij(k)=EbijΔbi(k)Fbij

(14)

式中：‖Δai(k)‖≤1；‖Δbi(k)‖≤1；Fai，Ebii，Fbii，Ebij，Fbij为适当维数的矩阵.

2 分布式鲁棒预测控制

针对具有不确定参数的城市路网分布式模型式(12)，本节采用基于LMI的分布式鲁棒预测控制方法，为每个子系统设计一个状态反馈控制器调节路口的各相位的绿灯时间，从而解决城市路网系统拥堵问题.在给出主要定理前，首先引入引理.

引理[15]设W，M，N，G为具有适当维数的实矩阵，其中G满足GTG≤I，W为对称矩阵，那么

W+NTGTMT+MGN<0

当且仅当存在常数ε>0，使得

W+ε-1NTN+εMMT<0

2.1 无穷时域“极小-极大”问题

首先无穷时域性能指标定义为

(15)

式中：Si和Ri为给定的对称正定加权矩阵；ΔXi(k)=ΔXi(k|k)为kT时刻子系统i的状态测量值；ΔXi(k+n|k)为kT时刻对(k+n)T时刻的状态预测值；ΔUi(k+n|k)为kT时刻求得的子系统i的(k+n)T时刻的最优控制输入；ΔUj(k+n|k)为kT时刻求得的子系统j的(k+n)T时刻的最优控制输入.

笔者的目的是设计一个无记忆状态反馈控制律为

ΔUi(k+n|k)=Ki(k)ΔXi(k+n|k)

(16)

(17)

稳定.

定理1对于闭环系统式(17)，如果存在矩阵Qi(k),Yi(k)，以及常数ξi1(k)，ξi2(k)，γi(k)，使得优化问题

(18)

(19)

(20)

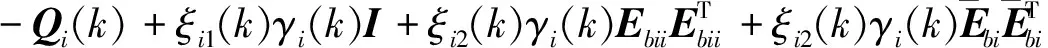
Vi(k+n+1|k)-Vi(k+n|k)≤

ΔUiT(k+n|k)RiΔUi(k+n|k)]

(21)

成立，则式(21)满足Lyapunov稳定条件：

Vi(k+n+1|k)-Vi(k+n|k)≤0

(22)

从而可知闭环系统式(17)渐近稳定.

将闭环系统式(17)代入不等式(21)得到

(23)

对式(23)应用Schur补引理可得

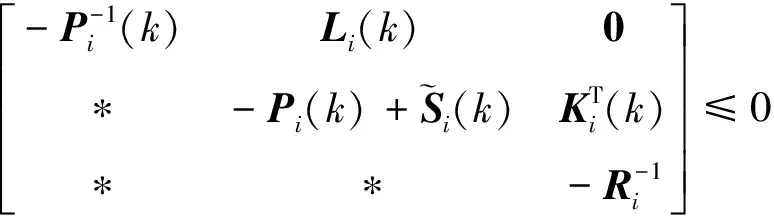
(24)

依次应用引理和Schur补引理可知：式(24)成立当且仅当存在常数εi1>0和εi2>0满足

(25)

式中：

将式(21)两边从n=0到n=∞求和可得

Ji(k)≤Vi(k)

(26)

令Lyapunov函数的上界为γi(k)，则由式(26)可得

Ji(k)≤Vi(k)≤γi(k)

(27)

即求解性能指标Ji(k)的上界可转化为求Vi(k)的上界.由式(27)可得

Vi(k)=ΔXiT(k)Pi(k)ΔXi(k)≤γi(k)

(28)

对式(28)应用Schur补定理即可得到不等式(19).

2.2 约束处理

为了使用线性矩阵不等式处理方法处理鲁棒模型预测控制，需要对约束式(4，5)进行必要的处理.

首先，根据问题式(9)求得UN后，式(4，5)的左右两边分别减去UN，并令uz,min为零，每个路口的信号周期均为C，则式(4，5)可转换为

(29)

(30)

式中w为单位列向量.

首先，对约束式(29)处理为

(31)

其中

(32)

进而将式(32)转换为线性矩阵不等式

(33)

同理，可将约束式(30)转换为

(34)

由式(34)可得线性矩阵不等式

(35)

2.3 分布式预测控制算法

对大规模的城市路网采用分布式鲁棒控制策略，能有效处理由测量误差、饱和流量的浮动等引起的交通状态的不确定性，且能降低系统的计算量.笔者提出的基于合作式的分布式鲁棒预测控制算法步骤具体如下：

Step 1在控制算法迭代初始时刻，设k=0,Ki=0.

Step 4求解得到控制量ΔUi(k)=Ki(k)ΔXi(k).

Step 5进入下一采样时刻，令k=k+1，返回Step 2.

3 控制仿真与实现

如图2所示，在仿真与实现中，考虑采用包含两个路口的系统.

图2 仿真结构图Fig.2 The structure of simulation

图2中共包含14条车道{L1,L2,…,L14},但是受控的车道只有{L5,L8}.各车道的转弯率如下：

t1,8=0.8,t3,8=0.2,t6,8=0.2,t9,5=0.2,t11,5=0.7,t13,5=0.2.定义p=ST，且p1=40,p3=50,p5=50,p6=50,p8=45,p9=50,p11=50,p13=50.

每个路口的信号灯周期均为C=60 s，其中，黄灯损失时间为L1=L2=16 s，每个周期含有四个相位，如图3所示.

图3 路口的相位示意图Fig.3 Phase diagram of intersection

稳态系统的XN和dN分别为

XN=[45,45,45,40,40,45,45,40]T

dN=[10,9,0,8,0,8,9,10]T

根据笔者所提的分布式鲁棒预测控制算法，在kT时刻在线求解优化问题式(18～20，33，35)，可求得每个采样时刻的控制输入量Ui(k)，现选取路口1作为分析对象，其控制输入如图4所示.

图4 路口J1的控制输入Fig.4 Control input of intersection J1

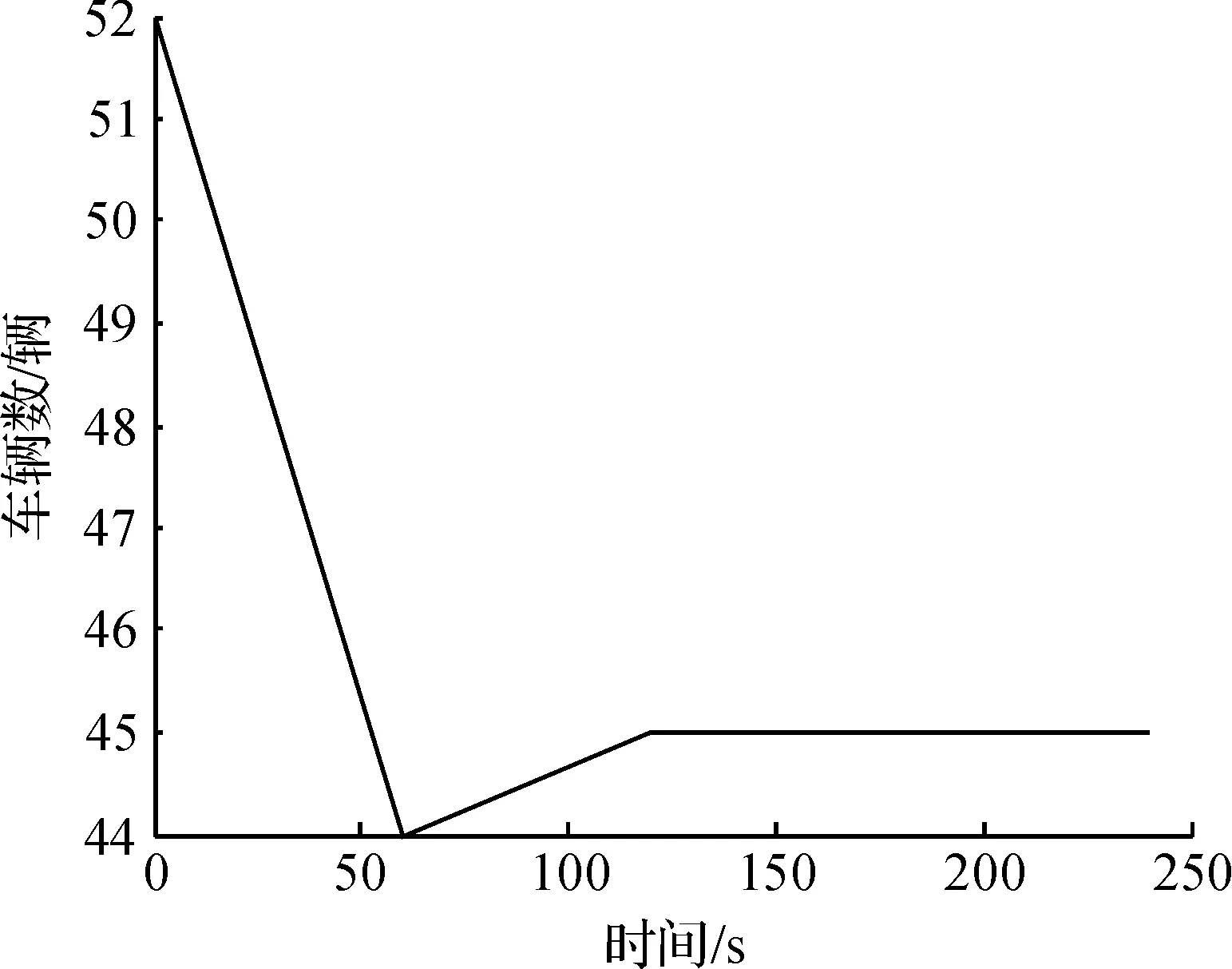
图5 路口J1的状态轨迹Fig.5 State trajectory of J1

综合图4，5可知：采用笔者提出的具有输入约束的状态反馈控制器作用下，在第一个信号周期内，J1路口各相位时间所占信号周期百分比变化较大，L5中的车队长度在该周期内迅速减小；在第二个信号周期内，各相位时间继续进行调整，从而使L5中的车队长度保持在稳态值.综上所述，在分布式鲁棒预测控制器的作用下，合理的红绿灯相位调配能防止拥堵状况的恶化，有效缓解路口的拥堵状况.

4 结 论

通将“存储与向前”模型改进为具有不确定性的

分布式路网系统模型，并且使得输入量满足一定的约束条件，采用分布式鲁棒预测控制方法解决了带有约束的凸优化问题.仿真研究表明：系统满足约束条件，具有较强的鲁棒性，能有效协调路网系统中的交通状况.

[1] 董红召，赵玉婷.基于PARAMICS的公交专用道时分复用方法研究及优化[J].浙江工业大学学报，2012，40(1)：65-69.

[2] PAPAGEORGIOU M, DIAKAKI C, DINOPOULOUV, et al. Review of road traffic control strategies[J]. Proceedings of the IEEE,2003,91(12):2043-2067.

[4] 杨旭华，李传告，陈光.基于K-最短路径的交通网络传输性能分析[J].浙江工业大学学报，2014，42(3)：249-252.

[5] 郭海锋，方良君，俞立.基于模糊卡尔曼滤波的短时交通流量预测方法[J].浙江工业大学学报，2013，41(2)：218-221.

[6] BURGER M, BERG M, HEGYI A, et al. Considerations for model-based traffic control[J]. Transportation research part c: emerging technologies,2013,35(9):1-19.

[7] 沈国江.城市区域交通智能分散控制研究[J].浙江大学学报(工学版)，2006(4)：585-589.

[8] GAZIS D C, POTTS R B. The oversaturated intersection[J]. Proceedings of the second international symposium on traffic theory，1963(2):221-237.

[9] 席裕庚,李德伟,林姝.模型预测控制—现状与挑战[J].自动化学报,2013,39(3)：222-236.

[10] ABOUDOLAS K, PAPAGEORIOU M, KOSMATOPOULOS E. Store-and-forward based methods for the signal control problem in large-scale congested urban road networks[J]. Transportation research part c: emerging technologies,2009,17(2):163-174.

[11] 承向军,杨肇夏.一种分布式交通信号控制方法及仿真实现[J].系统仿真学报,2005,17(8)：1970-1973.

[12] DE OLIVEIRA L B, CAMPONOGARA E. Multi-agent model predictive control of signaling split in urban traffic network[J]. Transportation research part c: emerging technologies,2010,18(1):120-139.

[13] ZHOU X, LU Y. Coordinate model predictive control with neighbourhood optimisation for a signal split in urban traffic networks[J]. IET intelligent transport systems,2012,6(4):372-379.

[14] DIAKAKI C, PAPAGEORIOU M, ABOUDOLAS K. A multivariable regulator approach to traffic-responsive network-wide signal control[J]. Control engineering practice,2002,10(2):183-195.

[15] 樊卫华，蔡骅，陈庆伟，等.时延网络控制系统的稳定性[J].控制理论与应用，2004，21(6)：880-884.

(责任编辑：陈石平)

Distributed robust model predictive control for urban road network

LIU Andong, LI Jia

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

The distributed robust predictive state feedback controller design problem is investigated in this paper for an urban road network with model uncertainty. Firstly, the urban road network topology model obtained from the extending of the “store and forward” linear model is divided into a distributed model. Considering the influence of uncertainty on urban road network systemun from road conditions change and the error of measurement, the distributed model with parameter uncertainty is derived for the urban road network system. Furthermore, a cooperative distributed robust predictive control algorithm is proposed, where the state feedback controller is designed by solving convex optimization problems online with LMIs. Finally, an example is given to demonstrate the effectiveness of the proposed method to alleviate the urban traffic congestion and optimize the light split.

distributed robust model predictive control; distributed model of the road network; uncertain parameters; LMI

2016-03-05

国家自然科学基金资助项目(61273117,61403344)

刘安东(1985—)，男，浙江衢州人，讲师，研究方向为网络化系统、模型预测控制等，E-mail：lad@zjut.edu.cn.

TP273

A

1006-4303(2016)06-0633-06