基于Midas的悬臂钢桁梁有限元分析及螺栓刚度识别

袁向荣， 刘 辉， 胡帮义， 蔡卡宏， 张 盼

(广州大学 土木工程学院， 广东 广州 510006)



基于Midas的悬臂钢桁梁有限元分析及螺栓刚度识别

袁向荣， 刘 辉， 胡帮义， 蔡卡宏， 张 盼

(广州大学 土木工程学院， 广东 广州 510006)

采用Midas Civil有限元软件中螺栓连接的建模方法，对螺栓连接的钢桁梁桥悬臂拼装施工状态进行有限元模拟，并将实测结构静力位移和有限元建模试算进行对比，对螺栓连接刚度进行识别。结果表明：将螺栓完全采用刚性连接模拟是不合理的，应采用一般弹性连接进行模拟。通过有限元建模试算，间接识别得到的螺栓连接刚度取值是合理的，位移预测误差为1.5%，获得了钢桁梁悬臂拼装施工状态较准确的有限元基准模型。

钢桁梁； 有限元分析； 螺栓连接； 参数识别

0 引 言

在土木工程钢结构桥梁中，螺栓连接是一种较常用的连接方式，根据受力状况不同可分为受拉螺栓与受剪螺栓，对于螺栓连接强度的验算在规范[1]中有较明确规定，然而对螺栓连接刚度的计算却不是很明确。在大跨度钢桁梁桥施工过程中，线型控制是一项重要内容[2]，线型控制需要比较准确预测结构在施工状态下的变形，螺栓连接刚度的取值，关系到有限元模型的准确性，对静力位移计算结果的精度影响较大，这涉及到螺栓连接刚度的取值和模型修正的问题[3]。对于有限元模型修正，何旭辉等[4]根据灵敏度的物理意义，提出了以结构设计参数为修改参数，以结构自振频率为目标函数的有限元模型修正方法。

针对螺栓连接的有限元建模，目前主要侧重于采用有限元软件对螺栓连接进行三维实体建模细部分析。夏卫明等[5]采用节点耦合来模拟螺纹幅的联接作用，提出了一种基于ANSYS的模拟盲孔螺栓联接的有限元仿真方法。沈诣等[6]针对大型结构螺栓有限元建模工作量大的问题，提出了一种对螺栓有限元模型的简化方法。沈国辉等[7]采用常见的三种有限元方法对螺栓节点板抗剪连接进行模拟计算，并给出了各方法的应用建议。高 旭等[8]利用ANSYS有限元分析软件建立了螺栓法兰连接结构的实体非线性有限元模型，并研究了螺栓不同预紧情况下模型的稳态响应。

有限元建模来模拟螺栓连接情况工作量较大，有的学者试图得到螺栓被连接件刚度的解析解，以便简化计算。杨国庆等[9]引入了假设垂直螺栓轴线的受压层在径向位置压应力的4次关系式，推导了被连接件刚度的计算公式，并通过试验获得了不同材料、尺寸所对应被连接件的刚度。随后又结合有限元分析与理论解析[10]，提出了一种精确计算被连接件刚度的半解析方法。李晓阳等[11]基于三维轴对称模型的弹性理论方法对螺栓连接中被连接件进行了建模，推导出了被连接件的刚度的理论解析解，简化了被连接件刚度的计算。

在实桥有限元分析方面，针对结构材料、构件尺寸、外部荷载以及施工过程中制作安装误差等因素对结构受力影响的随机性问题，刘剑等[12]运用Monte-Carlo随机有限元法对东江大桥施工全过程进行了随机有限元分析，徐晖[13]也对钢桁梁桥随机有限元分析进行了深入研究。王伟[14]采用组合有限元方法对某铁路64 m下承式简支钢桁梁桥进行了建模分析，模型考虑了节点板、横隔板、拼接板和螺栓等细部构件，较准确地模拟了桥梁实际受力。

根据笔者查询文献情况来看，实桥有限元模型中普遍没有考虑螺栓弹性作用而直接按刚性连接建模，这在实际工程中螺栓连接能够保证为刚性节点的情况下是可行的，但是在螺栓数量较少，个别螺栓未拧紧或被连接件局部翘曲不平整时则不能保证完全刚性连接，按刚性连接建模将导致误差很大，难以模拟实际结构的变形和受力。

本文以某悬臂钢桁梁桥模型为例，研究了带螺栓结构有限元建模的问题，提出了通过实测静力位移反算螺栓连接刚度的间接识别法，得到了模拟该悬臂钢桁梁的基准有限元模型，为桥梁施工控制位移和应力预测提供可靠的参考标准。

1 钢桁梁悬拼试验模型

某连续钢桁梁采用悬臂拼装施工，本试验模型选取拼装的某一工况进行模拟，模型共分6节，墩顶节编号为A0，其他节分别编号为A1～A5。单节尺寸为0.5 m×0.3 m×0.2 m，由不锈钢空心矩形管焊接而成，节与节之间采用Φ4 mm螺栓连接，A0节与钢管墩顶钢板之间亦采用Φ4 mm螺栓固定。加工好的实物模型如图1所示。A0节与钢管墩顶钢板之间螺栓固定如图2所示。杆件截面如图3所示。

图1 钢桁梁实物模型

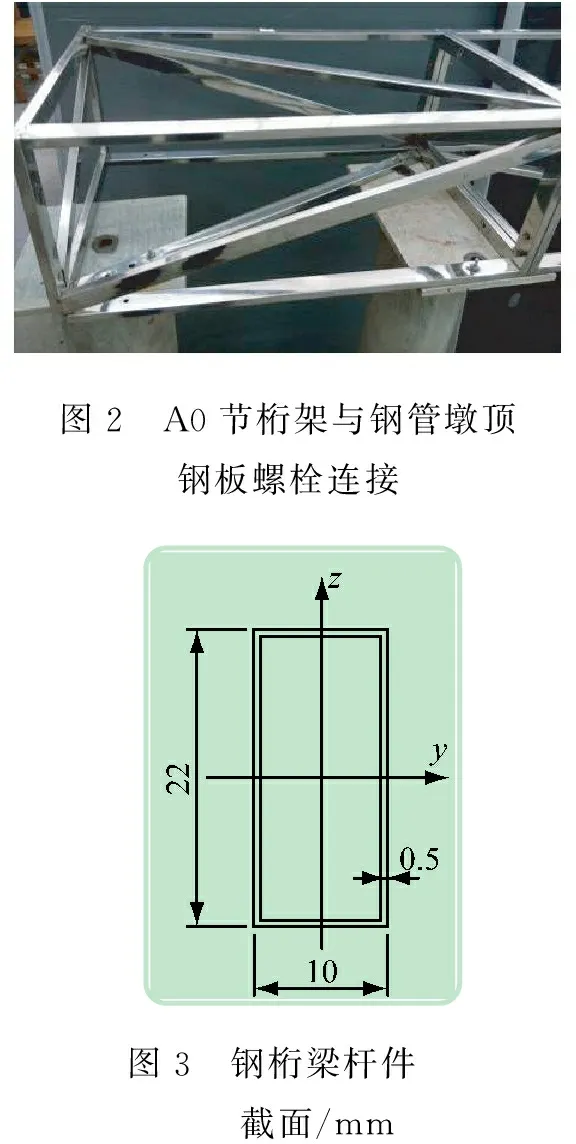
图2 A0节桁架与钢管墩顶钢板螺栓连接图3 钢桁梁杆件 截面/mm

材料截面面积A=3.1×10-5m2；截面抗弯惯性矩I=1.928×10-9m4；材料密度ρ=8.65×103kg/m3；弹性模量E=190 GPa，泊松比υ=0.3，线膨胀系数为1.2×10-5/℃。

2 钢桁梁在荷载作用下变形测量

以拼装好A0～A4节作为本试验工况，拼装时逐节安装螺栓，并用电动螺丝刀拧紧(见图4)。

图4 A0～A4节的钢桁梁模型

采用砝码对其进行加载，在A4节桁架右端角上各放置2个重1 kg的砝码，为了测得施加荷载引起结构的变形采用百分表对其进行测量，见图5。

图5 A0～A4节的钢桁梁端部位移百分表测量

施加荷载前后百分表读数分别为0.21、12.01 mm，故有A4桁架端部施加4 kg荷载引起结构的最大变形为11.8 mm。

3 钢桁梁有限元分析及螺栓连接刚度识别

3.1 有限元模型

采用Midas Civil有限元软件，依据钢桁架的尺寸，在软件中建立相应的节点和单元，由于模型加工的原因，桁架节点各杆件中心线并不相交于同一点，故均采用空间梁单元进行模拟。

桁架之间螺栓连接暂按刚性连接模拟，A0节桁架与钢管墩之间螺栓连接暂按固定支座考虑。建立的有限元计算模型如图6所示。

图6 螺栓暂按刚性连接考虑的有限元模型

3.2 有限元计算结果

有限元计算得到施加荷载后的变形图见图7。由图7可知P4节点最大变形6.5 mm。

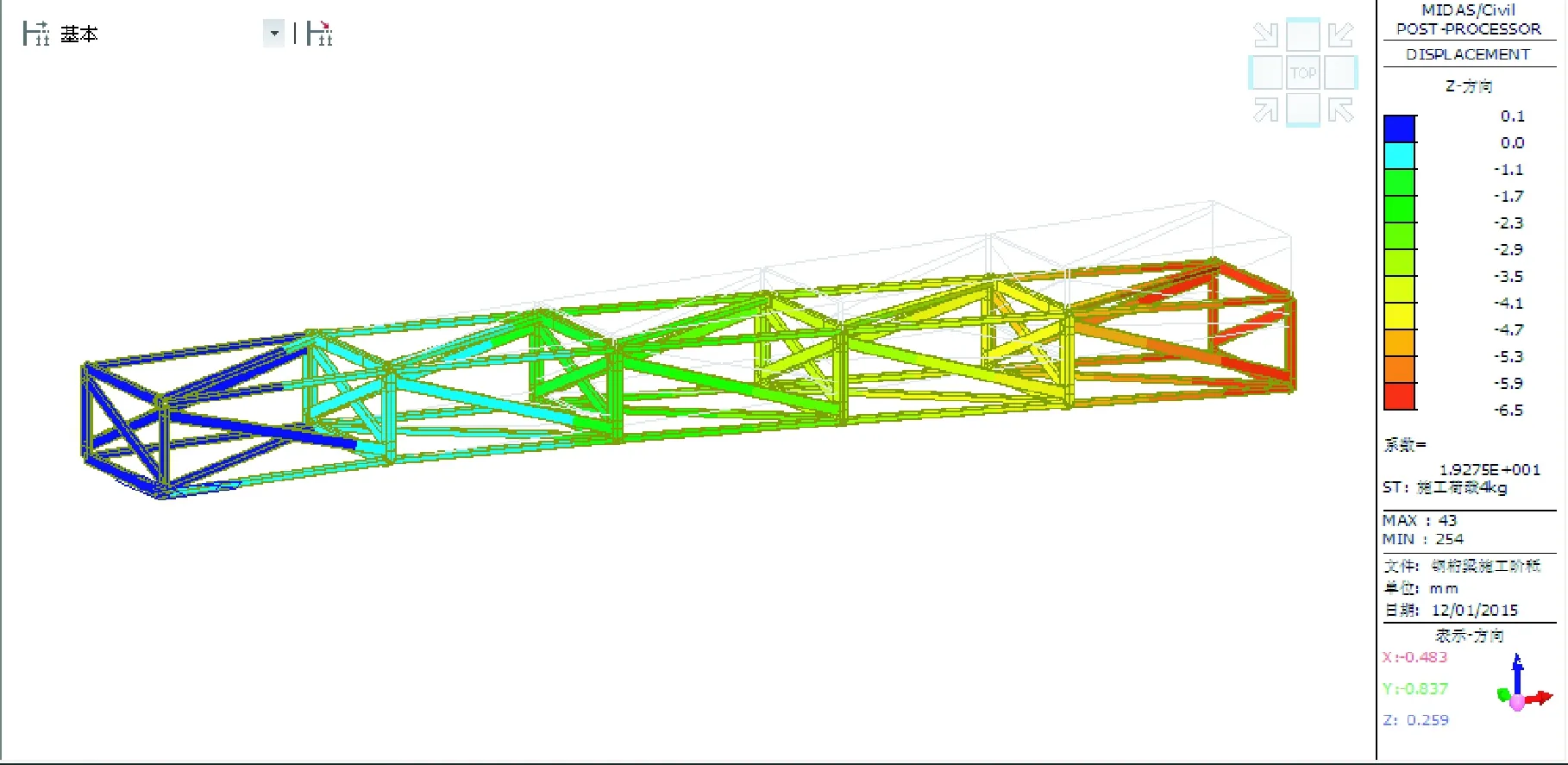
图7 钢桁梁施加荷载后的变形图

3.3 计算与实测结果对比及误差分析

当螺栓暂按刚性连接，建立的钢桁梁有限元模型，经加载荷计算得P4节点的最大变形为6.5 mm，同样条件下，实测钢桁梁的最大变形为11.8 mm，误差达81.5%，表明有限元模型没有很好地模拟实际情况，需要对模拟条件进行调整。究其原因，是由于桁架节与节之间以及桁架与钢管墩之间采用螺栓连接，属于弹性连接，建模初步按刚性连接考虑导致整体刚度偏大，从而导致计算结果偏小。

3.4 有限元模型中螺栓刚度的模拟

采用弹性连接来模拟螺栓连接，如图8所示，N1和N2节点之间采用弹性连接，其连接共有6个自由度，在Midas Civil软件中定义了6个刚度来进行描述，分别为SDx、SDy、SDz、SRx、SRy、SRz。其中：SDx、SDy、SDz分别表示连接在x、y、z轴方向的刚度；SRx、SRy、SRz分别表示连接在x、y、z轴方向的转动刚度。在这6个刚度中，影响本模型总体刚度的是SDx(纵向)和SDz(竖向)，故主要对该两刚度值进行识别。

图8 弹性连接模拟螺栓连接

3.5 螺栓纵向连接刚度的确定

对纵向连接刚度初步采用解析法确定，该刚度与螺栓的刚度CL和被连接件的刚度Cm有关。

根据文献[15]给出的温度与预紧力的关系式可知有:

(1)

对于螺栓的纵向刚度可以根据文献[16]中给定的公式进行计算，

(2)

式中：CL为螺栓的刚度(N/mm)；EL为螺栓材料的弹性模量，MPa；A为螺栓光杆部分截面积，mm2；As为螺栓的公称应力截面积，mm2；L1、L2、L3见图9。

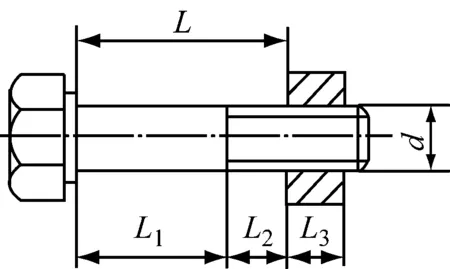
图9 螺栓构造尺寸图

本试验用的螺栓为直径d=4 mm普通螺栓。有：EL=2.06×105MPa；L1=0；L2=24 mm；L3=3.2 mm；A=πd2/4=12.6 mm2；As=8.78 mm2。代入式(2)得到：CL=67 kN/mm。

对被连接件的刚度Cm的计算采用文献[11]给出的解析公式初步确定。

(3)

式中：a为螺栓孔的半径,mm;b为螺母的半径,mm；h为被连接件的厚度，mm;υ为被连接件材料的泊松比;E为被连接件材料的弹性模量[11]，GPa。

对本试验模型，有：a=2.25 mm；b=3.5 mm；h=12 mm(考虑2 mm间隙)；υ=0.3；E=190 GPa；代入式(3)得到:Cm=2.07kN/mm,代入式(1)得到C=64.9 kN/mm。

由于存在安装误差和螺栓未拧紧等因素的影响，实际连接刚度往往与计算刚度有较大差别。在此，定义有效刚度系数λ来反映实际发挥效用的连接刚度，故有限元建模刚度:SDx=λC，其中：0≤λ≤1。

3.6 螺栓剪切连接刚度的确定

螺栓剪切连接刚度是螺栓在弯、剪共同作用下发生复杂变形的综合等效刚度[17]，计算式如下:

(4)

式中:K为螺栓剪切连接刚度；F为施加在螺栓上的剪切力；ΔS为螺栓沿剪切力方向产生的相对位移。K难以计算确定，故采用间接法识别。

3.7 螺栓刚度有限元试算法识别

分别取λ=0.1，0.2，…，1.0；SDz=5 000、500、50、5、0.5 N/mm，其他旋转刚度不约束，对模型结构进行有限元反复试算，得P4节点对应的纵向位移见表1。

表1 螺栓连接刚度不同取值时的P4节点位移

由表1可知,当λ=0.1、SDz=5 N/mm时，P4节点有限元计算位移为11.8 mm，与实测结果11.8 mm吻合。

3.8 刚度调整后有限元模型正确性验证

按照识别到的螺栓弹性连接刚度参数为SDx=6.49 kN/mm、SDz=5 N/mm，对悬臂钢桁梁拼装A5节后P4节点最大位移进行预测，以便对螺栓刚度取值合理性进行验证。重新建模计算得到的位移见图10。

由图10可知，P4节点有限元计算位移为16.2 mm。同时采用百分表对P4节点在A5节桁架右端角点施加4 kg荷载的变形进行了测量，如图11所示。

施加荷载前后百分表读数分别为7.30、23.75 mm，P4节点实测位移为16.45 mm。实测位移与计算位移16.2 mm之误差仅为1.5%，可见识别到的螺栓连接刚度基本与实际相符。基于识别到的螺栓连接刚度的有限元模型较准确的模拟了结构实际状态，可为后续桥梁施工控制提供基准有限元模型参考。

图10 拼装A5节后重新建模计算得到的位移

图11 拼装A5节后P4节点百分表实测位移

4 结 语

通过悬臂钢桁梁模型试验、有限元分析及螺栓连接刚度识别，可以得出以下结论：

(1) 在对采用螺栓连接的钢结构有限元建模过程中，将螺栓完全采用刚性连接模拟将导致计算变形值偏小，这种处理方法是不合理的，应采用一般弹性连接进行模拟。

(2) 采用一般弹性连接对螺栓进行模拟时涉及连接刚度的取值问题，由于实际安装误差的影响，有限元建模时的连接刚度与螺栓整体刚度及被连接刚度存在较大的区别，本文提出采用有效刚度系数来反映实际轴向连接有效刚度。

(3) 通过钢桁梁模型试验实测位移和有限元计算结果的对比分析可知，位移预测误差仅为1.5%；可见：识别到的螺栓连接刚度的取值是合理的。进一步验证了本文提出的采用实测静力位移后有限元试算的间接识别螺栓连接刚度的方法是可行的。

(4) 基于识别到的螺栓连接刚度的有限元模型较准确的模拟了结构实际状态，可为后续桥梁施工控制提供基准模型参考。

[1] 中华人民共和国建设部.钢结构设计规范GB50017-2003 [S].北京：中国计划出版社,2003.

[2] 邱式中.桥梁施工控制技术[J].预应力技术,2008(5):33-40.

[3] 陈德成,魏震松,曲广吉,等.有限元模型修正技术的工程应用[J].中国工程科学,2001,3(10):59-63.

[4] 何旭辉,余志武,陈政清.既有铁路钢桁梁桥基准有限元模型建立与验证[J].振动与冲击,2007,26(12):117-121.

[5] 夏卫明,郑 翔,杨晓俊.基于ANSYS的盲孔螺栓联接的有限元仿真[J].机械设计与制造,2009(7):42-44.

[6] 沈 诣,洪荣晶,高学海,等.大型结构的螺栓连接有限元简化方法与验证[J].机械设计与制造,2012(8):26-28.

[7] 沈国辉,陈 震,郭 勇,等.螺栓节点板抗剪连接的有限元模拟方法研究[J].工程力学,2013,30(1):119-125.

[8] 高 旭,曾国英.螺栓法兰连接结构有限元建模及动力学分析[J].润滑与密封,2010,35(4):68-71.

[9] 杨国庆,王 飞,洪 军,等.螺栓被连接件刚度理论的计算方法[J].西安交通大学学报,2012,46(7):50-56.

[10] 杨国庆,王 飞,洪 军,等.螺栓被连接件轴向刚度高精度计算的半解析方法[J].西安交通大学学报,2012,46(9):37-42.

[11] 李晓阳,王西旺,张琳琳,等.螺栓被连接件刚度的解析计算[J].北京工业大学学报,2015,41(4):514-518.

[12] 刘 剑,刘永健,徐 晖.刚性悬索加劲钢桁梁桥施工过程随机有限元分析[J].中国科技论文在线,2010,5(7):535-542.

[13] 徐 晖.钢桁梁桥施工过程Monte-Carlo随机有限元分析[D].西安：长安大学,2010.

[14] 王 伟.组合有限元法在钢桁梁桥计算中的应用研究[J].四川建筑,2004,24(6):94-95.

[15] 张红兵,杜建红.有限元模型中螺栓载荷施加方法的研究[J]. 机械设计与制造,1999(6):32-33.

[16] 成大先.机械设计手册[M].北京：化学工业出版社，2008.

[17] 张永杰,孙 秦.带预紧力受剪螺栓连接刚度分析[J].强度与环境,2007,34(4):22-25.

Finite Element Analysis to a Cantilever Steel Truss Girder and Study on Bolt Connection Stiffness Recognition Based on Midas

YUANXiang-rong，LIUHui，HUBang-yi，CAIKa-hong，ZHANGPan

(School of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

In order to simulate the cantilever construction state of steel truss girder that is connected by bolts is studied by using finite element method (FEM). The finite element software Midas Civil is applied. By comparing the measured results of static displacement and the results by FEM calculation, the bolted connection stiffness is identified successfully. The results demonstrate that the simulation by rigid connection of bolt is completely unreasonable, and it should be simulated by using the general elastic connection. The selection of the bolted connection stiffness identified by FEM pilot calculation is reasonable. The prediction error of static displacements is only 1.5%. It obtains the more accurate finite element benchmark model for the steel truss girder.

steel truss girder; finite element analysis; bolt connection; parametric recognition

2015-12-28

国家自然科学基金资助项目(51078093,51278137)；广州市科技计划项目(12C42011564)

袁向荣(1957-)，男，河北故城人，博士，教授，研究方向：桥梁工程、数字图像处理。

Tel.: 020-39366669； E-mail: rongxyuan@163.com

U 448.21+1； U 213.5+2

A

1006-7167(2016)08-0116-05