基于改进核范数的2DPCA人脸识别算法研究

刘 辉，马 文，何 强

(1.重庆邮电大学 通信新技术应用研究中心，重庆 400065； 2.重庆信科设计有限公司，重庆 400065)



基于改进核范数的2DPCA人脸识别算法研究

刘 辉1，2，马 文1，何 强1

(1.重庆邮电大学 通信新技术应用研究中心，重庆 400065； 2.重庆信科设计有限公司，重庆 400065)

传统的二维主成分分析法广泛应用于图像特征提取，为了使此算法更加有效，提出了一种结构化二维算法，即核范数2DPCA算法(N-2-DPCA)。该算法基于核范数重构误差准则，将核范数最优化问题转化为基于F范数的最优化问题，然后通过采用迭代方法寻找到最佳投影矩阵，最后运用最小欧氏距离规则识别出待识别人脸的身份。在此基础之上，将N-2-DPCA扩展到基于双边投影的算法(N-B2-DPCA)，采用曲线搜索算法寻找到双边投影矩阵，继而进行识别。最后将提出的算法在FERET和Yale B人脸数据库中进行人脸识别评估，实验结果表明所提出的算法与L1-2DPCA相比，重建误差降低了2.19%，识别率提高了2.03%，性能更好。

二维主成分分析法；特征提取；核范数；重建误差；双边投影

主成分分析法是一种经典的特征提取算法，它广泛应用于模式识别和计算机视觉等领域[1]。因此得到了深入的研究，从而扩展了大量版本。如加权主成分分析法(WPCA)和独立主成分分析法(ICA)。WPCA采用加权距离缓解异常值在投影方向的影响，ICA作为PCA算法的推广，不仅与变量的二阶相关，而且对它们的高阶存在依赖关系。PCA使数据不相关，而ICA使数据尽可能独立，PCA和ICA均是非监督算法[2]。

由于主成分分析法通常是将图像转换为一维向量，从而忽略了图像的结构信息。为了充分利用图像的结构信息，Yang等人提出了基于二维图像矩阵的主成分分析法(2-DPCA)，目前，2-DPCA广泛应用于模式识别和人脸识别当中。众所周知，2-DPCA在图像行上进行操作，而忽略了列上面的信息，为了能考虑到行和列上面的信息，提出了基于双边的2-DPCA算法。他们寻求到的投影矩阵可以提取行信息和列信息。PCA和2DPCA都是基于L2范数度量，对异常值不稳定，考虑到基于L1范数的算法对于异常值的稳健性更好，李等人提出了基于L1范数的二维主成分分析法(L1-2DPCA)，而此算法需要对每一个投影向量进行迭代优化，因此识别时间较长。

基于Frobenius范数(F范数)的方法基本上是采用欧氏距离来衡量不同图像之间的相似性。然而，同一个人的图像由于光照和视觉的不同，图像种类很多，基于F范数的算法对于这些干扰的鲁棒性很差，致使影响识别效果。为了缓解这个问题，顾等人提出了利用核范数度量代替F范数度量图像间的相似性。实验表明，核规范对光照变化不太敏感。因此，他们提出了一种基于PCA核范数算法，即Schatten 1-PCA[3]。

目前，基于核范数的最小化问题在模式识别和压缩感知领域引起了人们的广泛兴趣，核范数在本质上是矩阵秩的凸包络。基于核范数的优化方法已被用于低阶矩阵的恢复、人脸图像的自阴影去除等问题，福纳西尔等人提出将核范数问题转化成F范数，然后结合迭代加权策略解决核范数最小化问题[4]。

由文献[5]启发，本文提出了基于核范数的2DPCA算法(N-2-DPCA)，不同于2DPCA算法，本文模型使用核范数度量重构误差。此外，本文提供了足够的证据说明采用核范数来描述重构误差是有理论依据的。众所周知，顾等人也用范数描述变换后的数据，然而，在最大限度地提高标准算法中，他们对预期获得的投影矩阵强加了额外的约束，即PTP=PPT=I，这就要求投影矩阵是一个正交矩阵。在本文，笔者提出了精确的N-2-DPCA算法，由文献[5]和[6]启发，继而将N-2-DPCA扩展到基于双边投影的核算法(N-B2-DPCA)。

1 算法相关理论

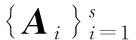
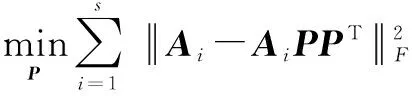
(1)

投影矩阵P通过计算协方差矩阵G最大的前r个特征值对应的特征向量可以获得。

图像矩阵的方法在模式识别中产生了一系列研究成果，具有代表性的是基于L1范数的2DPCA算法，其在低维特征空间中最大化L1范数方差。即为

(2)

众所周知，基于L1范数的2DPCA算法对于异常值的鲁棒性更好。然而，与2DPCA相比较，基于L1范数的2DPCA算法的每个主向量通过迭代运算获得，因此，此算法消耗更多时间。

在接下来的讲述中，笔者主要探讨基于核范数的2DPCA算法，采用迭代策略解决问题[7]。

2 研究核算法的动因

采用核算法获取投影向量最有力的一个理由是作为度量距离算法，核范数比L1和L2范数更加稳定可靠。例如，图1a和图1b为同一个人的图像，图1c为另外一个人的图像。然后通过采用核范数、L2范数和L1范数计算出相同人脸或不同人脸的图像距离。表1为不同范数下的图像间距离比较表。由表1可知，采用L1和L2范数，得到图1a和图1b之间的距离均大于图1a和图1c之间的距离，分类错误，然而，基于核范数得出的结论恰好相反，得出图1a和图1b之间的距离小于图1a和图1c之间的距离，分类正确。即可以对图像进行准确的分类。这个实验促使笔者采用核范数的标准。因此，对N-2-DPCA目标函数定义如下

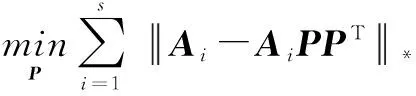
(3)

图1 3张不同的图像

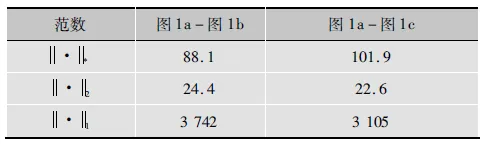
表1 不同范数下的图像间距离比较表

3 核算法研究

3.1 单边核算法

接下来将研究如何解决问题(1)，由文献[8]启发，将公式中的核范数优化问题转换为F范数优化问题，为此，给出下面的引理。

引理1：对于矩阵X∈Rp×q，

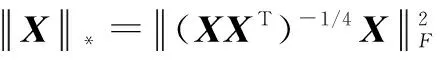
(4)

引理1表明核范数可以用F范数表示，为解决问题开避了一条新的道路。引理1中假定矩阵X的秩为r，其第a次权重可得

UΣVT是X的奇异值分解，Σ=diag(σ1,…,σr)，由引理1得，目标函数(1)可以改写为

(5)

Wi是权重矩阵，定义为

Wi=((Ai-AiPPT)(Ai-AiPPT)T)-1/4

(6)

采用迭代加权的方法来解决目标函数，该过程包括以下迭代。

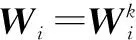
约束条件PPT=Ir

(7)

2)设定P=Pk+1，更新Wi如下

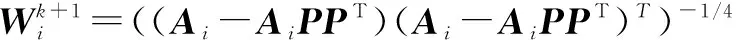
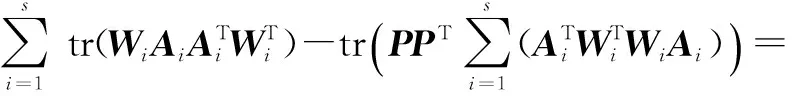
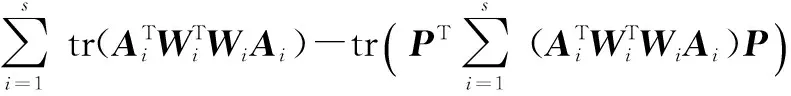
(8)

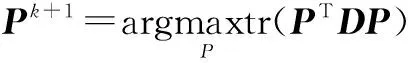
(9)

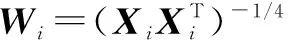
(10)

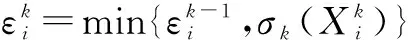
通过算法1获得投影矩阵P后，对于任意给定的测试样本A，它的特征矩阵B通过B=AP可以获得，特征矩阵B代替图像A进行分类。

算法1：N-2-DPCA迭代加权算法

输入：训练数据A1,…,As，投影维数为r。

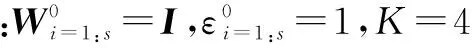
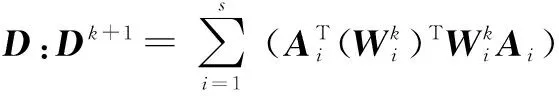
3)更新P:Pk+1=[d1,…,dr]，di是Dk+1的i个最大的特征值对应的特征向量。

4)计算Xi和εi：

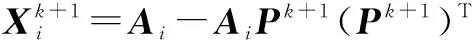
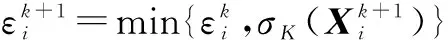
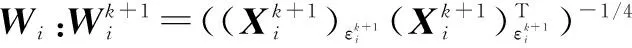
6)如果εi=0，执行第2)步，否则，从第2)步开始执行。

7)输出：最佳投影矩阵Pk+1。

3.2 基于双边核算法

N-2-DPCA采用单侧投影方案，该算法比PCA需要更多的系数来表示图像。N-B2-DPCA作为N-2-DPCA的延伸被提出来了，该算法左右投影方向均需要计算，此外采用N-B2-DPCA表示图像比N-2-DPCA需要更少的系数。双边N-B2-DPCA定义如下：

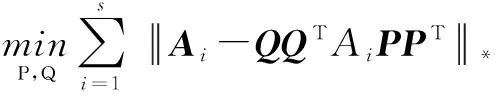
QTQ=It

(11)

在式(6)中，P∈Rn×r和Q∈Rt×m分别为左右乘积投影矩阵，接下来更新变量P和Q。

指定Q=Qk，更新P如下

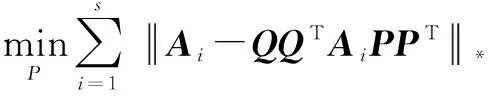
(12)

指定P=Pk+1，更新Q如下

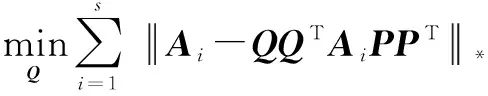
(13)

与解决N-2-DPCA算法类似，同样采用迭代加权法解决问题(12)和(13)。

对于式(12)，迭代包括以下过程：

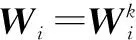
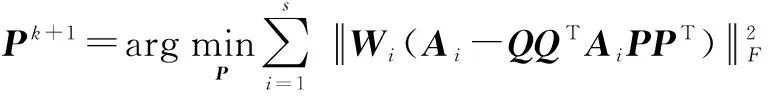
约束条件PPT=Ir

(14)

2)令P=Pk+1，更新Wi如下：

(15)

最关键的一步是解决方程(14)的最优化问题。目标函数(14)可以改写为

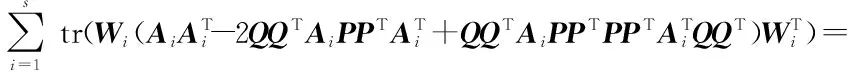
(16)

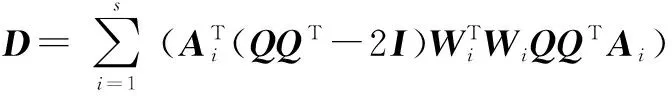
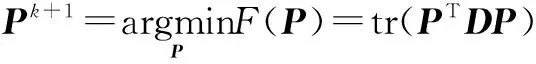
(17)

在方程(17)中，矩阵D是不对称，通过寻找特征向量，不能找到问题(17)的解决方案，因为非对称矩阵的特征值和特征向量不能全面表示图像信息。

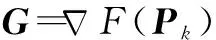
(18)

(19)

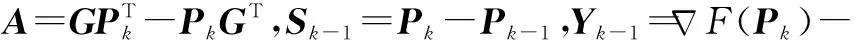
基于算法2，问题(12)的解决步骤总结后得到算法3。

算法2 ：解决问题(15)的曲线搜索算法

1)初始化：P0，r，终止误差因子ε，k=0。

2)搜索方向Y(τ)如方程(18)。

3)选择合适的步长τk如方程(19)。

4)更新Pk+1=Y(τk)。

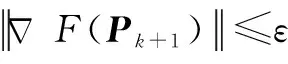
6)输出：最优矩阵Pk+1。

算法3：解决问题(12)的迭代加权算法

输入：训练数据A1,…,As，投影数量r，左投影矩阵Q。

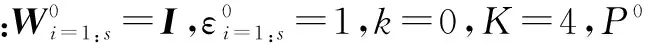
2)通过算法2更新P。

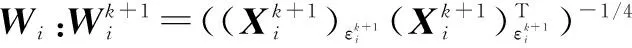
4)如果εi=0，执行步骤5，否则，从第2)步执行。

5)输出：最优矩阵Pk+1。

算法4：解决问题(11)的交替迭代算法

输入：训练数据A1,…,As，投影数量r，t。

1)初始化：Q0=I，k=0。

2)采用算法3更新Pk+1。

3)采用算法3更新Qk+1。

4)如果标准(21)满足，执行步骤5)，否则，从第2)步执行。

5)输出：最优矩阵Pk+1，Qk+1。

算法4总结了N-B2-DPCA的详细步骤，在算法4中，使用平均重建误差相对率来检查N-B2-DPCA的收敛性，平均重建误差在第k步定义为

(20)

算法4的收敛性可以通过相对差分为基础的收敛准则来判断[11]。

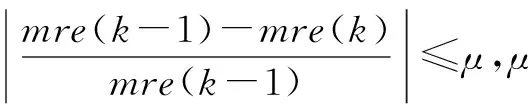
(21)

通过算法4获得投影矩阵P和Q，对于任意给定的训练样本A，图像A的特征矩阵C通过C=QTAP获得，特征矩阵C用来表示图像进行分类识别。

4 实验与分析

作为一种非监督子空间分析算法，最新提出的2DPCA-L1算法不利用标记信息。因此，为了公平比较，在方法性能比较中均采用非监督子空间算法。比较的算法包括2DPCA-L2，MPCA，PCA-L2，PCA-L1，2DPCA-L1以及本文算法。其中，2DPCA-L1，2DPCA-L2和MPCA是以图像矩阵为基的算法，而PCA-L1和PCA-L2是以图像向量为基的算法，这里的PCA-L2算法即是经典的PCA算法。

(22)

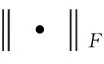
图2 归一化的FERET人脸数据库样本图像

图3 经矩形噪声处理后的部分FERET图像

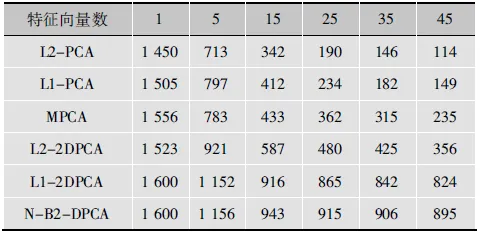
表2 不同算法下平均重建误差随特征向量数变化表

表2为L2-PCA、L1-PCA、MPCA、L2-2DPCA、L1-2DPCA以及N-B2-DPCA这6种算法下平均重建误差随特征向量变化表。图4展示了这六种算法的平均重建误差随特征量个数的变化规律。可以发现，当特征值个数大于10，N-B2-DPCA性能优越性体现的更加明显。L1-2DPCA和L2-2DPCA性能好于L1-PCA、L2-PCA和MPCA，与L1-2DPCA相比，重建误差降低了2.19%。图4为平均重建误差与特征量个数关系图。

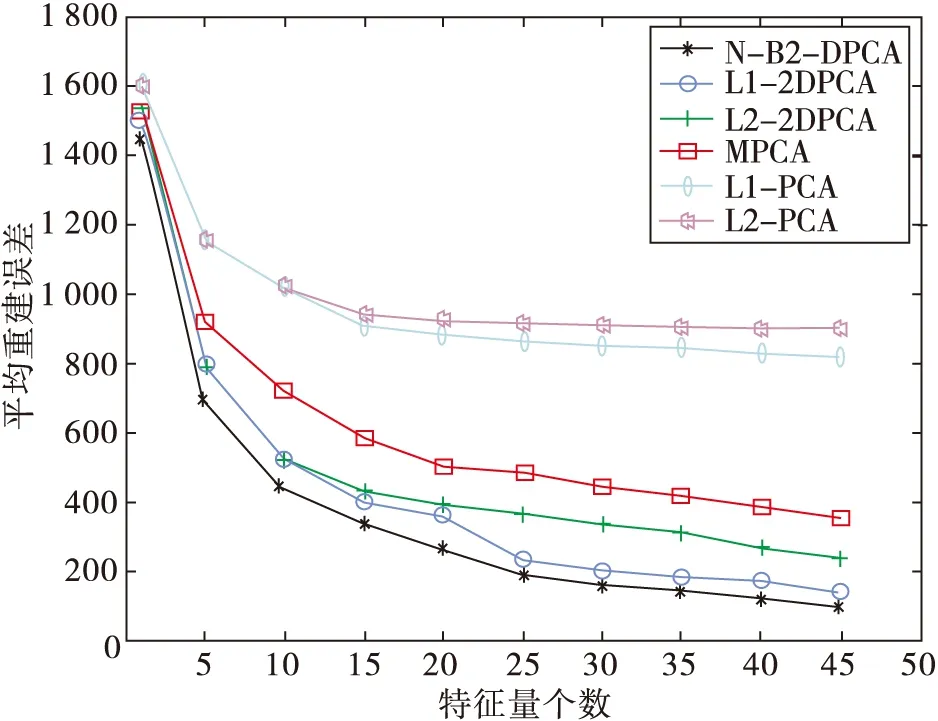
图4 平均重建误差与特征量个数关系图

在第二个实验中，采用了扩展的Yale人脸数据库，此数据库包含38个主题，每个主题有32张图片，每张图像重塑为96×84。根据光照条件不同，将数据库图像分为5个子集。每个子集中的2个样本图像如图5所示。对于每一个主题，一半的图像被随机选择出来作为训练图像，余下的作为测试图像。图6显示了2DPCA、L1-2DPCA以及N-B2DPCA这3种算法识别率随特征向量数的变化曲线图。由图可知，采用本文算法识别率更高，与L1-2DPCA相比，识别率提高了2.03%，这是由于采用搜索算法获得的投影向量提取图像信息的能力更强，最终保障了较高的识别率[13]，表3为3种人脸识别算法不同特征向量数对应的识别率表。

图5 扩展Yale B的5个子空间的样本图像

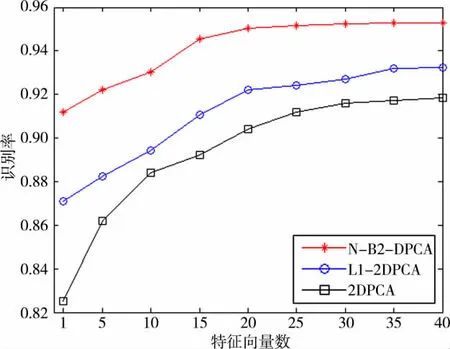
图6 3种算法识别率随特征向量数变化曲线图

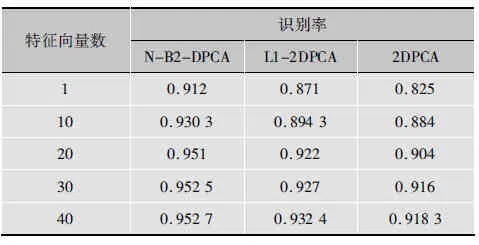
表3 3种人脸识别算法不同特征向量数对应的识别率表

5 结论

本文提出了一种基于二维的子空间模型，即基于核范数的2DPCA核范数图像特征提取算法。该模型的核心思想是利用核范数代替常规的L2-范数度量重构误差。该模型通过迭代加权算法求解。此外，N-2-DPCA进一步扩展到N-B2-DPCA，基于双边投影的2DPCA核算法压缩率比单边投影的2DPCA核算法更高。在人脸数据库上的实验结果表明所提出的方法优于其他特征提取方法，与L1-2DPCA相比，重建误差降低了2.19%，识别率提高了2.03%。

[1]JOLLIFFE I T. Principal component analysis[M].2nd ed. New York： Springer-Verlag，2002.

[2]赵庆苓. 主成分分析在人脸识别研究中的应用[J]. 贵州大学学报(自然科学版)，2010，27(5)：67-71.

[3]焦斌亮，陈爽. 基于PCA算法的人脸识别[J]. 计算机工程与应用，2011，47(18)：201-203.

[4]钟秀峰. 基于改进的主成分分析的人脸识别算法研究[D]. 汕头：汕头大学，2012.

[5]KONG H，WANG L，TEOH E K， et al. Generalized 2D principal component analysis for face image representation and recognition[J]. Neural networks，2005，18(5/6)：585-594.

[6]YANG J， LIU C. Horizontal and vertical 2DPCA-Based discriminant analysis for face verification on a large-scale database[J]. IEEE transactions on information forensics & security， 2008， 2(4)：781-792.

[7]CANDES E J，RECHT B. Exact matrix completion via convex optimization[J]. Communications of ACM，2012，55(6)：111-119.

[8]FORNASIER M，RAUHUT H，WARD R. Low-rank matrix recovery via iteratively reweighted least squares minimization[J]. Siam journal on optimization， 2010， 21(4)：1614- 1640.

[9]WEN Z，YIN W. A feasible method for optimization with orthogonality constraints[J].Mathematical programming， 2013， 142(1/2)：397-434.

[10]LIWICKI S，TZIMIROPOULOS G，ZAFEIRIOU S，et al. Euler principal component analysis[J]. International journal of computer vision，2013，101(3)：498-518.

[11]MASHHOORI A，JAHROMI M Z. Block-wise two-directional 2DPCA with ensemble learning for face recognition[J]. Neurocomputing，2013，108(2)：111-117.

[12]WANG H. Block principal component analysis with L1-norm for image analysis[J]. Pattern recognition letters，2012，33(5)：537-542.

[13]GAO Q，GAO F，ZHANG H，et al. Two-dimensional maximum local variation based on image Euclidean distance for face recognition[J]. IEEE transactions on image processing， 2013， 22(10)：3807-3817.

刘 辉(1966— )，教授级高工，硕士生导师，主要从事通信新技术研究；

马 文(1988— )，硕士生，主研嵌入式方向；

何 强(1991— )，硕士生，主研计算机视觉、机器学习。

责任编辑：闫雯雯

Human face recognition based on improved nuclear norm 2DPCA algorithm

LIU Hui1，2，MA Wen1，HE Qiang1

(1.ResearchCentreforApplicationofNewCommunicationTechnologiesn，ChongqingUniversityofPostsandTelecommunications，Chongqing400065，China；2.ChongqingInformationTechnologyDesigningCo.，Ltd.，Chongqing400065，China)

The traditional two dimensional component analysis is widely used for image feature extraction. In order to make the algorithm more effective， a structural 2-D method is presented， namely， nuclear norm-based 2-DPCA(N-2-DPCA).The algorithm is based on nuclear norm reconstruction error criterion， by means of converting the nuclear norm-based optimization problem into a series of F-norm-based optimization problems， then by using iterative method to find out the optimal projection matrix， finally adopting the minimum Euclidean distance rule to identify the identity of face recognition. In addition， the N-2-DPCA is extended to a algorithm based on bilateral projection(N-B2-DPCA)， by using the curvilinear search algorithm to find the bilateral projection matrix， then recognize the identity of face recognition. Finally， the proposed algorithm is evaluated in FERET and Yale B face database， the experimental results show that the proposed algorithms compared with L1-2DPCA， the reconstruction error is lower 2.19%， the recognition rate is increased by 2.03% and it performs better.

2-D principal component analysis； feature exaction； nuclear norm； reconstruction error； bilateral projection

刘辉，马文，何强. 基于改进核范数的2DPCA人脸识别算法研究[J]. 电视技术，2016，40(11)：126-131. LIU H，MA W，HE Q. Human face recognition based on improved nuclear norm 2DPCA algorithm [J]. Video engineering，2016，40(11)：126-131.

TP391

A

10.16280/j.videoe.2016.11.026

重庆市研究生科研创新项目(CYS14143)；重庆市研究生创新基金资助项目(CYS151166)

2016-01-12