双重不确定系统对偶控制与RLS辨识控制比较分析
2016-12-21杨恒占钱富才
杨恒占,高 韵,钱富才
(1.西安工业大学 电子信息工程学院,西安710021;2.西安理工大学 自动化与信息工程学院,西安710048)
双重不确定系统对偶控制与RLS辨识控制比较分析
杨恒占1,高 韵1,钱富才2
(1.西安工业大学 电子信息工程学院,西安710021;2.西安理工大学 自动化与信息工程学院,西安710048)
为了辨识双重不确定性系统未知参数,跟踪系统目标输出值,本文对未知参数随机系统分别进行了对偶控制和最小二乘(RLS)辨识控制.提出了双重不确定随机系统对偶控制和最小二乘辨识控制策略.通过双重不确定随机系统仿真,比较分析了对偶控制和最小二乘辨识控制策略的性能.结果表明:该对偶控制策略用于双重不确定性随机系统参数辨识时实时性和稳定性优于最小二乘辨识控制;随机系统在运行过程中未知参数变化时,对偶控制策略仍可有效跟踪系统目标输出值,且对偶控制跟踪误差和切换之前保持一致,而RLS辨识控制不能有效跟踪系统目标输出值,跟踪失效.
双重不确定系统;对偶控制;辨识控制;实时性
随着生产系统愈加复杂,不确定性增加,分析和研究系统所建立的数学模型也愈加困难.事实上,生产过程的数学模型都只是实际系统运行过程的近似[1],不仅受到随机噪声干扰,而且系统模型本身也可能存在不确定性,即系统存在双重不确定性.对于双重不确定性系统,需要对模型中未知参数进行辨识,对采集到的信息进行一定的算法处理,构造出最接近实际的模型.对于双重不确定性系统,传统方法首先对系统进行激励,收集系统运行信息,然后对收集的信息进行处理,辨识出未知参数,最后再依据辨识结果进行控制.在这个过程中,冀望不仅通过辨识参数来减少系统的不确定性,而且能有效跟踪目标[2-4].因此,迫切需要寻找一种有效的控制方法,把对参数进行辨识的学习系统与对系统进行目标跟踪的控制系统结合起来作为整体进行考虑.文献[5]提出对偶控制思想:跟踪理想输出;学习未知参数.由于控制系统要求控制量要尽可能的小以获得好的控制效果,而学习系统则要求控制量要尽可能的大以对系统的状态和参数进行有效辨识,两种作用互相冲突.因此需要在控制与辨识之间实现权衡[6-9],文献[10]通过引入新息序列方差的方法,在控制和辨识方面有良好的权衡,而学习因子具有开环特性,因此受到一定限制.文献[11]对各种次优对偶控制方法进行了分析,取得了一定成果.由于把控制时间分割为若干个单一的阶段,控制器具有主动学习性能.为了阐明对偶控制的良好性能,本文针对双重不确定性随机系统,在系统参数发生变化的情况下,分别采用递推最小二乘(Recursive Least Square,RLS)辨识控制和对偶控制,通过双重不确定随机系统仿真,对最小二乘辨识控制和对偶控制策略的性能进行比较分析,以实现双重不确定性系统未知参数的辨识,系统目标输出值的跟踪.
1 控制策略
1.1 问题描述
考虑如下离散随机动态系统
C(z-1)x(k+1)=D(z-1)u(k)+e(k+1)
(1)
式中:u(k)为控制量;x(k)为系统输出;e(k)为高斯白噪声;k为离散时间;α1,α2,…,αn,β0,β1,…,βn为系统参数;C(z-1)和D(z-1)为n阶多项式,z-1为系统的延迟函数,且有
C(z-1)=1+α1z-1+α2z-2+…+αnz-n;
D(z-1)=β0+β1z-1+β2z-2+…+βnz-n
当系统参数已知时,只有一种不确定性,即系统外部噪声带来的不确定性.若系统中存在未知参数,或运行过程中参数发生变化,系统就具备了双重不确定性特征:①不受控制的系统外部噪声;②系统中可通过学习进行逼近的未知参数.本文考虑具有双重不确定性的系统,控制器设计既要能够对未知参数进行辨识学习,又要能够跟踪控制目标.
考虑离散随机动态系统最优跟踪控制问题,即
(2)
式中:J为系统性能指标;xr(k+1)为系统设定的目标值,不失一般性,取值为零;E(·)为期望.对离散随机动态系统,控制器在k时刻除了知道系统的先验信息,k时刻之前系统的控制量{u(0),u(1),…,u(k-1)}也可知道,以及直到k时刻的测量量{x(1),x(2),…,x(k)}.这些信息是控制器在k时刻进行设计的基础,可记为以下集合形式,即
I(k)={u(0),…,u(k-1),x(1),…,x(k)}
其中I(k)为系统的信息集合.
对于动态未知随机系统,分别采用RLS辨识控制方法和对偶控制方法求控制量u(k),使性能指标J最小.
1.2 RLS辨识控制
辨识控制通过最小二乘方法辨识出未知参数的估计值,把辨识出的参数替代未知参数,系统成为已知系统,再使用常规随机控制方法进行控制.最小二乘辨识过程中,通过伪随机序列对系统进行激励,根据系统输出信息对未知参数进行辨识.
用最小二乘法对未知参数进行辨识,系统可改写为
(3)
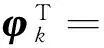
θ=[α1,…,αn,β0,…,βn]T.
用伪随机序列产生N个输入信号u(k)(k= 0,1,…,N-1),依次施加到实际系统上,测量系统对应的输出,可得
xN=ΦNθ+eN
(4)
式中:ΦN为辨识信息矩阵;xN为输出矩阵;eN为高斯白噪声矢量;N为辨识总次数,且有
xN=[x(1),x(2),…,x(N)]T;
eN=[e(1),e(2),…,e(N)]T.
已知xN和ΦN,求θ使估计准则H最小,即
参数估计值为
(5)


(6)
其中f0,f1,…,fn为最小方差控制的系数.
RLS辨识控制把对未知参数的辨识学习和对系统的目标跟踪分为完全隔离的两个阶段,第一阶段进行单纯的参数辨识,第二阶段则依据辨识的结果进行单纯的目标跟踪控制.
1.3 对偶控制
对偶控制能够在对系统未知参数进行辨识的同时,对目标进行跟踪.对偶控制原理如下:①给未知参数赋初值,系统运行产生输出;②根据系统输入、输出信息通过卡尔曼滤波对参数进行辨识;③用辨识的参数设计控制器对系统进行控制;④重复②、③步骤.
系统模型由差分形式转化成状态方程,即

(7)
式中:x(k+1)为系统输出;Φ(k)为控制信息;y(k+1)为系统参数;e(k+1)为高斯白噪声.且有
Φ(k)=[u(k),…,u(k-m),-x(k),…,-x(k-n)];
y(k)=[β0(k),β1(k),…,βn(k),α1(k),α2(k),…,αn(k)]T;其中β0(k),β1(k),…,βn(k),α1(k),α2(k),…,αn(k)为系统未知参数.
通过Kalman滤波,可得状态方程中参数y(k)的递推估计为
(8)

为系统实现一边控制,一边学习,根据动态规划方程,对性能指标加入学习权重λ(k),且大于1,则性能指标为
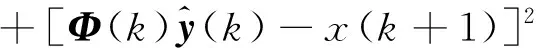
(9)
对式(9)求导容易得出最小性能指标,因此,使得性能指标最小的控制量为
(10)
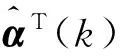

2 仿真及分析
单输入-单输出随机系统为
x(k)+α1x(k-1)+α2x(k-2)=β0u(k-1)+β1u(k-2)+e(k)
(11)
式中:e(k)为高斯白噪声,且e(k)~N(0,0.05);定义Ω为参数集合,且有
Ω={β0,β1,α1,α2}.
假定系统参数真值在20步发生切换:
20步前参数真值Ω1={1,0.5,-1.7,0.7};
20步后参数真值Ω2={0.5,-1,1,-1}.
2.1 RLS辨识控制仿真
采用最小二乘对参数进行辨识,经过20步后对参数辨识的结果见表1.可以看出辨识结果已经接近真值.图1为对目标值的跟踪控制情况.在系统参数切换前,通过最小方差控制对其进行控制,可以看出,系统输出值很快趋近目标值.第20步参数发生切换,由于系统运行过程中仍然使用最初的辨识参数值,最小方差控制最小方差控制无法对系统进行有效的控制.
2.2 对偶控制仿真
图2为对偶控制对未知参数的辨识,其中实线是参数真值,虚线是系统参数辨识值.由图2可以看出,在系统参数切换前,参数辨识值逐渐逼近参数真值;系统参数切换后,参数辨识值仍然能够逐渐逼近真值.
表1 最小二乘参数辨识结果
Tab.1Parameteridentificationresultsofrecursiveleastsquares

参数值β0β1α1α2辨识值1.0910.521-1.6950.695真值1.0000.500-1.7000.700

图1 RLS辨识控制目标跟踪

图2 对偶控制参数辨识
图3为对目标值的跟踪控制情况.在系统参数切换前,系统输出值经过短暂动荡后(对应参数辨识最初阶段)很快趋近目标值.第20步参数发生切换后,系统输出值经过短暂动荡后(对应新参数辨识最初阶段)很快又趋近目标值.RLS辨识控制尽管在系统新启动情况下初期阶段控制效果好于对偶控制,但是付出的是前期系统专用于参数辨识的代价,系统运行过程汇总参数发生漂移或切换,就无法达到控制目标.而无论是系统新启动或参数发生切换时,对偶控制均能够重新调整控制策略,对控制目标进行良好跟踪.

图3 对偶控制系统目标跟踪
3 结 论
1) 本文针对双重不确定性随机系统,分别进行对偶控制和递推最小二乘辨识控制,提出了双重不确定随机系统对偶控制和最小二乘辨识控制策略.仿真实验表明,该控制策略稳定性、实时性优于传统辨识控制.
2) 系统在运行过程中参数发生突变时,对偶控制可进行系统参数有效辨识,而RLS辨识控制难以有效跟踪系统目标输出值.
3) 文中针对线性系统,而对于非线性系统的未知参数辨识和目标输出值跟踪误差还有待深入研究和讨论.
[1]PIEREL,MICHAELA,DAVIDAK.SomePropertiesoftheDualAdaptiveStochasticControlAlgorithm[J].IEEETransonAutomaticControl,1981,26(2):1001.
[2]TSEE,BARS.AnActiveAdaptiveControlforLinearSystemswithRandomParametersviaDualControlApproach[J].IEEETransonAutomaticControl,1973,18(11):109.
[3]FELDBAUMAA.DualControlTheory:I[J].AutomationandRemoteControl,1960,21(2):874.
[4]FELDBAUMAA.DualControlTheory:II[J].AutomationandRemoteControl,1960,21(3):1033.
[5]FELDBAUMAA.DualControlTheory:III[J].AutomationandRemoteControl,1961,22(2):12.
[6]QIANFC,XIEG,LIUD,etal.OptimalControlofLQGProblemwithanExplicitTrade-offBetweenMeanandVariance[J].InternationalJournalofSystemsScience,2011,42(2):1957.
[7]LID,QIANFC,FUPL.VarianceMinimizationApproachforaClassofDualControlProblems[J].IEEETransAutomaticControl,2002,47(12):2010.
[8]BRIANDO.Twenty-fiveSeminalPapersinControl[J].IEEEControlSystemsMagazine,2002,20(1):69.
[9] 郭尚来.随机控制[M].北京:清华大学出版社,1999.
GUOShanglai.RandomControl[M].Beijing:TsinghuaUniversityPress,1999.(inChinese)
[10] 李鹏波,胡德文.系统辨识基础[M].北京:中国水利水电出版社,2006.
LIPengbo,HUDewen.SystemIdentificationBasis[M].Beijing:ChinaWaterConservancyandHydropowerPress,2006.(inChinese)
[11] 郑大钟.线性系统理论[M].北京:清华大学出版社,2002.
ZHENGDazhong.TheLinearSystemTheory[M].Beijing:TsinghuaUniversityPress,2002.
(inChinese)
(责任编辑、校对 张 超)
Comparative Analysis of Dual Control and RLS Identification Control for System with Dual Uncertainties
YANGHengzhan1,GAOYun1,QIANFucai2
(1.School of Electronic Information Engineering,Xi’an Technological University,Xi’an 710021,China;2.School of Automation and Information Engineering,Xi’an University of Technology,Xi’an 710048,China)
In order to identify unknown parameters and to track system target output value in dual uncertainty system,dual control and recursive least squares (RLS) identification control are presented for the stochastic system.The control strategy of double dual control and the recursive least squares identification controland is put forward.Through dual uncertain stochastic system simulation, the dual control and least squares identification performance of the control strategy are comparatively analyzed.The results show: The dual control strategy is used for dual uncertainty parameter identification of stochastic system,its realtime performance and stability are better than the least squares identification control; When the unknown parameters of stochastic system change in the running process,dual control strategy can still be effective track system for the target output value,and the tracking error is consistent with the value before switching;RLS identification control cannot effectively track system output value,and fails to track.
dual uncertainties system;dual control; identification control;real-time
10.16185/j.jxatu.edu.cn.2016.10.013
2015-11-23
国家自然科学基金重点项目(61533014);国家自然科学基金(61273127; 61304204);陕西省国际科技合作重点项目(2015KW-024);陕西省教育厅专项科学研究计划项目(16JK1364)
杨恒占(1976-),男,西安工业大学讲师,主要研究方向为随机系统、最优控制.E-mail:yanghengzhan@xatu.edu.cn.
TP13
A
1673-9965(2016)10-0843-05
