基于信噪比的GNSS随机模型分析

柴大帅,王胜利,卢秀山

(1.山东科技大学 测绘学院,青岛 266590;2.山东科技大学 海洋工程研究院,青岛 266590)



基于信噪比的GNSS随机模型分析

柴大帅1,王胜利2,卢秀山2

(1.山东科技大学 测绘学院,青岛 266590;2.山东科技大学 海洋工程研究院,青岛 266590)

使用差分进行定位时,观测值仍然含有残余的大气延迟以及受到噪声影响。由于信噪比能够很好的反映噪声部分的影响,卫星的高度角与信号传播路径上的大气延迟有很高的相关性,所以利用基于卫星高度角和信噪比的随机模型可以一定程度的削弱这些误差的影响。本文以实测数据对等权随机模型、高度角随机模型和信噪比随机模型的处理效果进行分析,实验结果证明，信噪比随机模型的处理效果最好,高度角随机模型次之,等权随机模型的处理效果最差。同时本文分析了信噪比对伪距观测值质量的影响,并在此基础上对这三种随机模型进行分析,实验结果显示:在数据预处理时选取合理的信噪比可以使这三种模型的定位精度有所提高。

信噪比;GNSS;等权随机模型;高度角随机模型;信噪比随机模型

0 引 言

卫星导航定位中存在各种误差源,如大气延迟、卫星钟差、接收机钟差、噪声等[1]。通常情况下,要想获得较高精度的点位定位结果一般选用差分技术。虽然差分之后卫星钟差、接收机钟差被消除,大气延迟误差被削弱,但是仍然存在残余的大气延迟和未被削弱的多路径等误差[2-3]。由于不同环境、不同卫星、不同观测时刻的观测值的精度是不同的,因此,建立比较切合实际情况的随机模型,尤其是在观测环境不好的情况下,对提高GNSS定位精度具有重要的现实意义[4]。当前随机模型有很多,比如等权随机模型、高度角随机模型和信噪比随机模型等[5]。等权随机模型最简单,但是没有考虑到实际情况。高度角随机模型是依据卫星高度角和信号传播路径上大气延迟具有相关性而建立的模型,较符合实际情况,是应用较广泛地随机模型,但是实际中并不是高度角越大,观测值质量就会越好。信噪比随机模型是根据观测值信噪比(SNR)信息建立的模型,而信噪比信息能够很好的反映观测值的质量情况,通常情况下信噪比越大,观测值的质量也会越高,对此很多学者对信噪比模型进行了研究[6-7]。三系统接收机接收到的卫星数目较单系统多,极大的改善了卫星的空间几何结构[8]。本文使用三系统数据(GPS、GLONASS、BD)在分析信噪比对伪距质量影响的基础上,分析了这三种随机模型对伪距差分定位结果的影响,实验结果表明，选择合理的信噪比能够提高定位精度。

1 数学模型

1.1 组合差分定位模型

在双差模型中,伪距差分定位的观测方程为[9]

(1)

1.2 随机模型

1) 等权随机模型

等权模型一般可以分位两种:一种是不考虑观测值之间任何相关性的随机模型;另一种是只考虑观测值之间数学相关性的随机模型。本文采用的是只考虑观测值之间数学相关性的等权随机模型,对应地协方差矩阵能够通过误差传播定律得到[10]:

(2)

式中: σ称为观测值的单位权中误差;P称为双差观测值的权矩阵。

2) 高度角随机模型

不同的卫星在不同时刻具有不同的高度角,导致卫星发射的信号具有不同的传播路径,卫星高度角越低,信号传播经过的路径就越长,大气延迟等误差通常会越大,观测值的质量也就越差[11]。根据高度角建立的随机模型有很多,常用的是[12]:

(3)

式中,E为卫星高度角。

3) 信噪比随机模型

信噪比指信号功率和噪声功率的比值,通常用载噪比(C/N0)表示,单位为dB-Hz.它主要受到相关性能、天线增益性能和多路径效应的影响。依据信噪比建立的随机模型能够很好地反映观测数据的噪声情况[13],通常情况下信噪比越高,观测值的质量越好,信噪比随机模型可以表示为[7]

(4)

式中: C/N0表示信噪比; Ci通常取1.61×104mm2[6].

利用误差传播定律可以得到高度角和信噪比随机模型的双差观测值协方差矩阵为[10]:

(5)

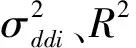
(6)

(7)

式中: r、i分别表示参考卫星与非参考卫星的编号; f、u分别表示参考站与移动站的编号。

2 算例分析

为了比较这三种随机模型对伪距差分定位的影响,本文采用实测的三系统静态数据进行分析,系统间采用等权策略。实验地点为山东科技大学校园内,基站架设在S2实验楼顶,坐标精确已知,移动站架设在南门附近,部分有遮挡。基站和移动站相距约326 m,观测时间2015年5月26日9:38-12:42,卫星截止高度角为10°,采样率为0.05 s.

为了直观地反映信噪比对观测值质量的影响程度,本文做了如下实验:运用自编软件对实验数据进行载波双差解算,求出移动站的坐标。将求出的移动站坐标带入公式(1)中,求出双差伪距观测值,可以认为是精确的双差观测值,然后将与通过观测文件求出的双差观测值进行求差,将划分为不同的区间,统计在各个区间中信噪比各自所占的比例。本文取1小时实验数据对上述方案作出统计,结果如表1、表2所示。

表1、表2直观地反映了信噪比对伪距的影响程度,从表中能够看出信噪比对C/A码与P2码伪距的影响相似。随着信噪比的增大,信噪比所在的|ΔPt-ΔPi|区间有变小的趋势。这说明信噪比越大,观测值的质量越好,噪声越小,观测值越接近真值。比较表1、表2可以看出在|ΔPt-ΔPi|<1 m的区间,表1中占95.78%,表2中占93.78%,所以信噪比对C/A码与P2码伪距质量影响程度基本一致。

由表1、表2可以看出,如果不对观测数据进行处理,直接将观测值用于定位计算,将会有一些质量不好的观测数据被引入观测方程中,影响定位精度。

图1、图2示出了这三种随机模型不经过预处理时的C/A码与P2码伪距双差定位结果。

从图1、图2可以看出等权随机模型的结果跳动比较严重,这主要是由衍射、噪声等误差引起的,而信噪比随机模型和高度角随机模型的结果较平滑,基本没有跳动情况,并且图1、图2中(a)的结果优于图1和图2中(b)的结果,这说明信噪比随机模型和高度角随机模型都能够降低这些误差对定位结果的影响。对于高度角随机模型,低高度角的卫星观测值被赋予了较小的权重,可以降低残余的大气延迟等误差的影响,但是对于高度角较高的卫星观测值如果受到这些误差的影响,将仍然会被赋予较高的权重,影响定位的结果。对于信噪比随机模型,只要卫星信号受到干扰,信噪比就会变小,所以,信噪比较高度角更能准确的反映卫星观测值的质量。虽然这两种随机模型都能够提高定位结果的精度,但是信噪比随机模型的效果优于高度角随机模型。

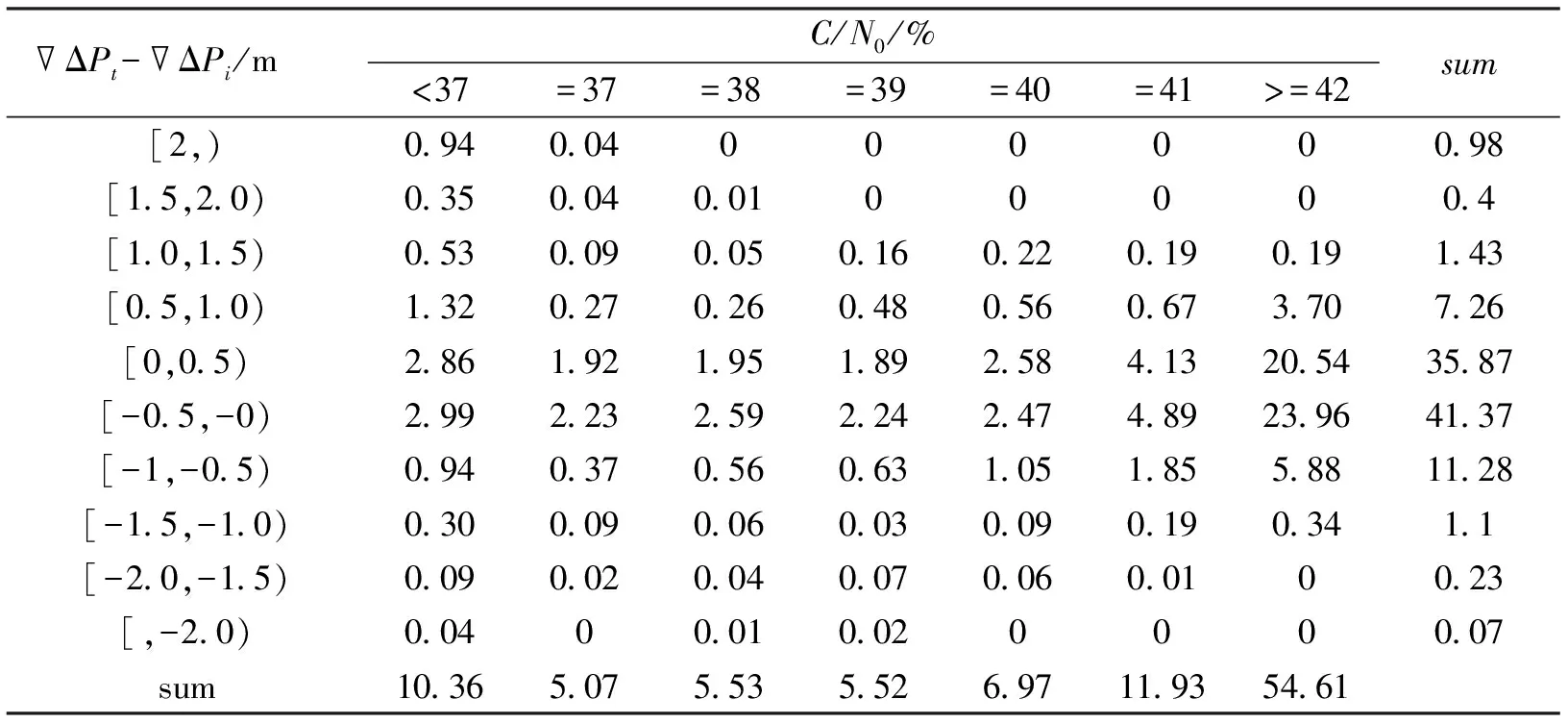
表1 信噪比对C/A码伪距的影响统计

表2 信噪比对P2码伪距的影响统计

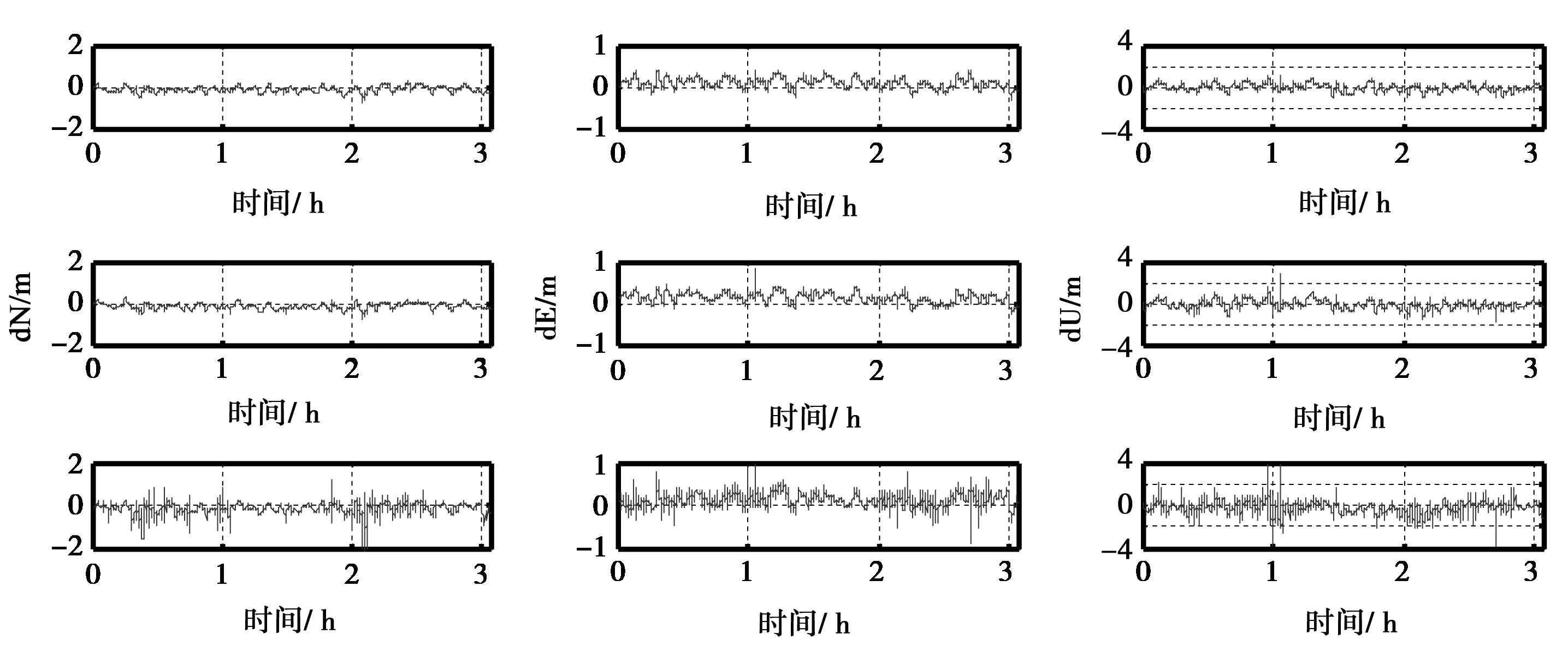
图1 C/A码伪距双差(第一行信噪比模型；第二行高度角模型；第三行等权模型)

图2 P2码伪距双差(第一行信噪比模型;第二行高度角模型;第三行等权模型

为了体现信噪比对伪距的影响本文做了如下实验:以信噪比为条件对数据进行预处理,将质量不好的卫星剔除。图3、图4分别为加入数据预处理的C/A码和P2码伪距双差结果。本文C/A码的信噪比阈值取29,P2码的信噪比阈值取39.

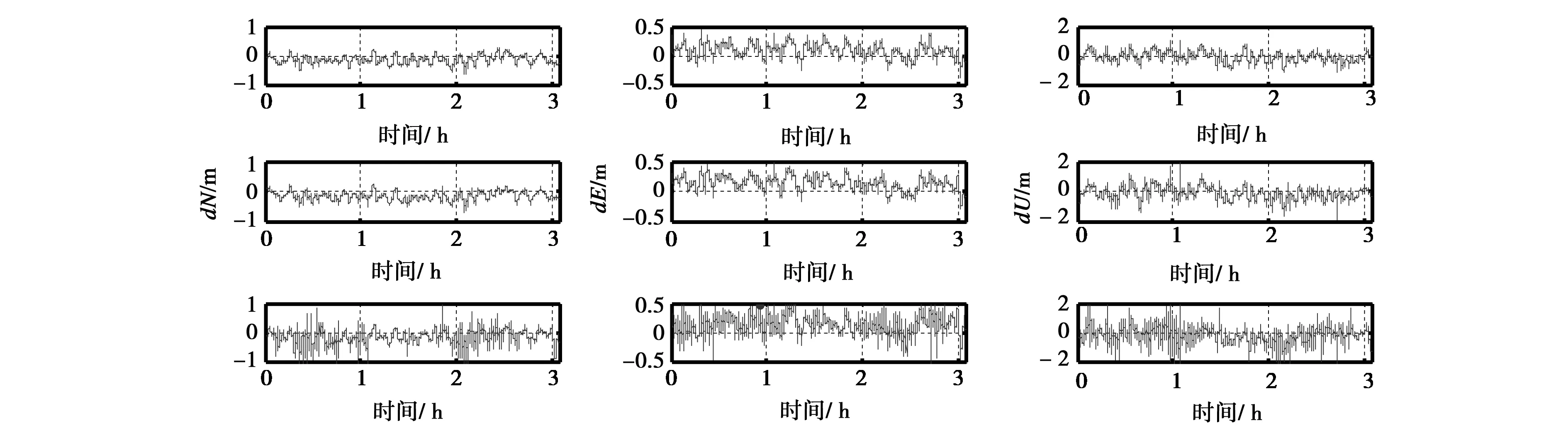
图3 预处理后的C/A码伪距双差(第一行信噪比模型;第二行高度角模型;第三行等权模型)

图4 预处理后的P2码伪距双差(第一行信噪比模型;第二行高度角模型;第三行等权模型)

比较图3、图4可以看出信噪比随机模型和高度角随机模型优于等权随机模型,但是相比图1、图2而言,图3、图4的等权随机模型的结果有所提高,并且等权随机随机模型的结果与另外两种随机模型的结果差距较图1、图2减小。这是因为通过预处理将观测值质量较差的卫星剔除,质量较高的观测值被用于定位计算,而信噪比随机模型和高度角随机模型的本质是对质量较差的方程赋予较小的权重,降低其在定位解算中的作用。

表3 不进行预处理的不同模型N、E、U方向的RMS值

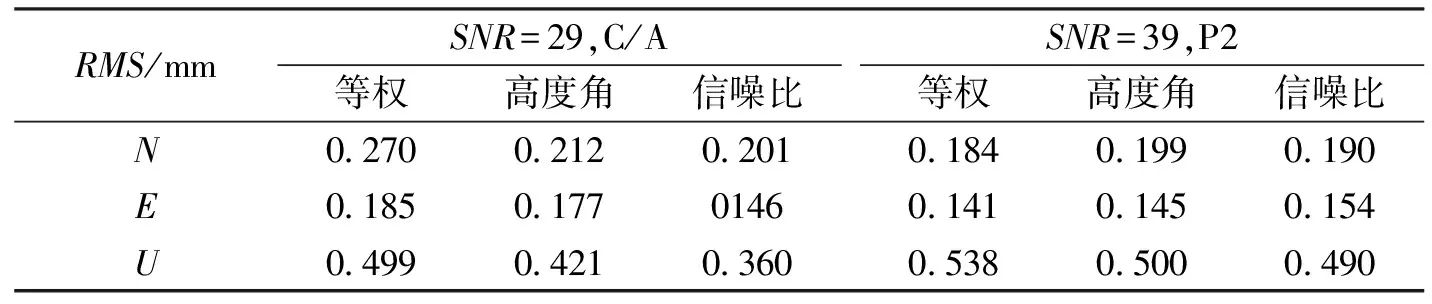
表4 进行预处理的不同模型N、E、U方向的RMS值

表3列出了不根据信噪比进行预处理时这两组实验N、E、U方向的RMS,表4列出了根据信噪比进行预处理时这两组实验N、E、U方向的RMS.从表3可以看出,对于SNR=0的两栏,信噪比随机模型和高度角随机模型的RMS都优于等权随机模型,并且信噪比随机模型的RMS小于高度角随机模型的RMS.当观测数据依据信噪比进行预处理时,从表4中可以看出,这三种随机模型的RMS较不进行预处理时的RMS都有一定程度的减小,并且等权随机模型的RMS与另外两种随机模型的RMS差异较不采用信噪比进行预处理时变小。所以,通过合理的选择信噪比大小使高质量的卫星观测值用于定位计算中,能够提高定位结果的精度。

3 结束语

本文在利用信噪比对伪距质量的影响进行统计分析的基础上,使用等权随机模型、高度角随机模型和信噪比随机模型对伪距双差定位结果的影响进行分析得出如下结论：

1) 信噪比随机模型和高度角随机模型优于等权随机模型,有助于提高定位精度,但是信噪比模型要优于高度角随机模型；

2) 信噪比信息较高度角信息能更好地反映卫星观测值的质量情况；

3) 合理选择信噪比大小可以一定程度的提高伪距双差定位精度；

4) 通过合理选择信噪比大小将高质量的卫星用于定位计算,能够减小等权随机模型与高度角随机模型和信噪比随机模型之间定位结果的差距。

本文的方法仍然存在不足之处:信噪比信息不是强制输出的,有些观测文件中可能没有信噪比信息;通过合理选择信噪比剔除质量不好的卫星来提高定位精度的方法,会使参与定位计算的卫星数目变少,对于卫星数目较少的情况仍需进一步研究。

[1] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:78-89.

[2] 吉绪发,卢辰龙.GPS多路径误差滤波方法比较研究[J].测绘通报,2015(4):10-13.

[3] 刘超,王坚,胡洪,等.动态变形监测多路径实时修正模型研究[J].武汉大学学报(信息科学版),2010,35(4):481-485.

[4] 刘志强,黄张裕,金建平.利用卫星高度角和信噪比提高GPS定位精度的试验分析[J].测绘工程,2008,17(4):54-58.

[5] 徐锐,黄丁发,廖华,等.VRS动态随机模型建模方法的综合比较[J].武汉大学学报(信息科学版),2010,35(3):290-293.

[6] BRUNNER F K, HARTINGER K H,TROYER L,etal. GPS signal diffraction modeling: The stochastic sIGMA-Δ model[J]. Journal of Geodesy, 1999(73): 259-267.

[7] HARTINGER K H, BRUNNER F K. Variances of GPS phase observations: SIGMA-ε model[J]. GPS Solutions, 1999, 4(2): 24-35.

[8] 潘林,蔡昌盛,戴吾蛟,等.一种联合多历元信息的GPS/BD组合单点定位方法[J].测绘通报,2015,(2):5-9.

[9] 王胜利.多系统融合GNSS定位地面增强关键技术研究[D].南京:东南大学,2013:13-17.

[10]戴吾蛟,丁晓利,朱建军.基于观测值质量指标的GPS观测值随机模型分析[J].武汉大学学报(信息科学版),2008,33(7):718-722.

[11]刘超,王坚,路鑫,等.GPS载波相位观测值随机模型的比较研究[J].测绘科学,2010,35(67):151-154.

[12]刘云朋,尹潇,楼立志.高度角信噪比联合随机模型的抗差GPS/COMPASS实时差分定位算法分析[J].大地测量与地球动力学,2014,4(4):145-148.

[13]辛星,崔有祯,李继林,等.一种BD/GPS接收机单频定位精度分析[J].测绘科学,2016,41(2):34-38.

Comparing GNSS Stochastic Models Based on SNR

CHAI Dashuai1, WANG Shengli2,LU Xiushan2

(1.CollegeofGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266590,China; 2.InstituteofOceanEngineering,ShandongUniversityofScienceandTechnology,Qingdao266590,China)

When DGNSS was used, observations still were affected by noise and residual atmospheric delay. Because the SNR can well reflect the impact of the noise, and the elevation angle of satellite has a correlation with atmospheric delay of signal propagation path, so stochastic model of satellite elevation angle and SNR can be used to weaken these influences. In this paper, these models of identity, elevation angle and SNR was analyzed in this paper, and experimental results show that the effect of SNR model was the best, elevation angle model was followed, and identity model was the worst. Simultaneously, the affect of SNR to Quality of pseudo-range was analyzed in this paper, and on this basis these models were analyzed. The results show that selecting appropriate SNR value in preprocessing can increase the accuracy of these models.

Signal to Noise Ratio; GNSS; identity stochastic models; elevation angle stochastic models; SNR stochastic models

10.13442/j.gnss.1008-9268.2016.05.008

2016-04-10

大地测量与地球动力学国家重点实验室开放基金(编号:SKLGED2015-3-1-E)； 海洋公益性行业科研专项经费(编号:201305034)

P228.4

A

1008-9268(2016)05-0042-06

柴大帅 (1991-),男，硕士生,主要从事GNSS数据处理研究。

王胜利 (1981-),男，博士、讲师,主要从事GNSS数据处理等研究。

卢秀山 (1961-),男，博士、教授、博导,主要从事3S集成等研究。

联系人： 柴大帅 E-mail: 1552101053@qq.com