基于改进蚁群最优算法配电网故障恢复重构的研究

文 | 肖惜明，贾铁军，张福杰，刘文文

基于改进蚁群最优算法配电网故障恢复重构的研究

文 | 肖惜明，贾铁军，张福杰，刘文文

配电网故障恢复重构问题是一个非常复杂的多时段、多目标、多约束、多组合的非线性优化问题，最后得到的解是一系列开关动作的组合。然而，由于此问题的复杂性和难测性，很难简单地从数学优化的角度去找到它的最优解，若想要得到能够满足要求的可行解运算的时间也非常长。在实际应用过程当中，有工作经验的调度员通常可以根据自己常年工作经验和一些启发式的方法来寻找最优方案，从而能够快速有效地达到恢复供电的目的。

故障恢复是一个非线性的优化问题，解决此类问题主要是应该确定最优的搜索方向，常用的方法是启发式搜索方法。Taylor等人曾经提出过基于启发式方法的最优搜索树的方法。启发式搜索方法所得到的结果的好坏一般与网络结构有关，不能保证肯定找到最优解。其它方法像模拟退火法（Simulated Annealing）、爬山法和列表寻优法（Tabu search）等，通常我们将这些方法统称为搜索算法。

蚁群算法作为现代智能型算法家族的新成员之一，它具有十分特殊的优良特性，现在已经在电力系统的许多领域中得到应用。近年来，由于蚁群算法的优越性能，使其在许多领域得到非常广泛应用，如电力调度问题（Scheduling Problem）、功率优化（Continuous Optimization）等。

恢复重构的数学模型

一、恢复重构的数学模型

按照不同的应用场合和目的，可以定义不同的恢复重构的数学模型，一般来说，其数学模型可描述如下：

其中，f（S,X）是数学模型的目标函数，S为控制变量，X为状态变量，g为不等式约束，h为等式约束，T为所求问题的解空间。

二、目标函数

对于恢复重构来说，其主要目的是：

1.尽量恢复停电用户的供电

2. 降低网损

3. 平衡负荷

4.开关操作的次数尽量小

上述目的目标函数为：

（1）尽量恢复停电用户的供电

式（5）中：Li为支路长度，Si和Smax分别为支路负荷和最大允许负荷。

（2）网损最小

式（6）中：ik为支路k上的电流，Rk为支路k上的电阻，n为配电网的支路数。

（3）平衡负荷

式（7）中：St为元件的实际负荷，Stmax为元件最大允许负荷，n为元件数。

（4）开关操作的次数

式（8）中：Nop为开关操作的次数。

三、 约束条件

配电网的约束条件及其数学描述：

1.配电网的潮流约束

2. 馈线的容量约束

3. 线路电流的约束

4. 母线电压的约束

5.网络结构的约束

它们的目标函数为：

（1）配电网的潮流约束

其中： Di为节点i上所连的出线的集合，为节点i的注入有功功率、无功功率，为节点 i的有功负荷、无功负荷，连在节Z点i上的第m条支路上流过的有功功率、无功功率，连在节点 i上的第m条支路上的有功损耗、无功损耗。

（2）馈线的容量约束

（3）线路电流的约束

（4）母线电压的约束

（5）网络结构的约束

改进型蚁群最优故障恢复算法

一、算法策略

为了叙述方便，作如下定义：Skt为第k只蚂蚁t时刻连入树的节点集合；Wkt为第k只蚂蚁t时刻未连入树的节点集合；Ekt为t时刻在两节点集合间所有可选路径的集合；Ak为t时刻Ek中引入的新的可选边的集合；Pk为t时刻各t条路径上的信息素概率。具体的更改步骤如下面所示：

令某待恢复供电的配电网络中全部联络开关闭合后形成的联通图中的可操作开关集数为K，且K与独立环路数对应，任意开关集i中可操作支路数为（ i＝1－K）。因此故障恢复规划重构问题可用如下模型表示：任一点i（ i＝1－K）与ni条相关支路（环路i中的可操作支路）连接，任一点相连的各支路中必须且仅能确定一条支路断开。q（i,j）（j＝1－ni）代表与节点i相关联的支路j上的“信息素密度”。

蚂蚁遍历生成树的过程如下：

令各相关支路上的初始“信息素”密度为C0，蚂蚁的数目为m，在蚁群最优（Ant Colony Optimization，ACO）算法的每次迭代过程的一个周期中，让所有蚂蚁都集中在第1个点。每只蚂蚁根据转换概率来选择与该点相连的一条边并让其开断。转换概率与各节点相连的ni条相关支路上释放的“信息素”密度有关。当m个蚂蚁都选好后，集中到第2个点，直到选择出所有K个点相连支路中应予以唯一分段的开关为止，这就形成了m个样本解。

Step2：蚂蚁k在t时刻先以概率Pkt随机从集合Ekt中选择边l（s，w）。

Step3：检查是否Ekt中包含w？如果包含则断开l，返回Step2；否则执行Step4。

Step5：Wkt是否为空？若是则结束，所有的负荷节点都被连入树；否则执行Step6。Step6：更新集合令 。

在选择信息素更新时，设置一个中心控制蚂蚁为路径更新依据，其作用是找出当前最优解。

在完成对一个周期的搜索后，对各支路上的“信息素”密度进行更新，即：

式中：ρ为系数， 1－ρ代表周期t至t＋1之间各支路上的“信息素”蒸发系数；τ（t）为周期t内各支路上留下的总“信息素”量； Δτ（t,t＋1）为周期t至周期t＋1期间各支路上的“信息素”改变量，即：

式中Δτr（t, t+1）为周期t至t＋1之间第r只蚂蚁释放在各支路上“信息素”的数量，其表达式为

式中：Q为常量；fr为第r只蚂蚁恢复供电策略方案所对应的网损目标函数值。为计算网络中的线路损耗，本文采用了前推回代的配电网潮流算法。

在1个周期中，第r只蚂蚁根据转换概率pr（i,j）来选择并分段与节点i相关的某一支路 ，其表达式为：

由式（6）可知，pr（i,j）取决于各节点相关支路上“信息素”密度的大小。在故障恢复重构算法程序实现过程中，根据各支路的“信息素”密度，采用类似于遗传算法的转盘赌的方式确定某环路的分段开关。

当一次循环完成后，ACO算法从所有蚂蚁形成的m个重构方案中选择具有最小目标函数值的解方案，并与当前保存的最优解方案进行比较。如果该最优解方案比当前保存的最优解方案还要好，则用该最优解方案更新当前保存的最优解方案，否则维持当前的最优解方案不变。重复上述过程，直至达到预先指定的最大迭代次数Nmax为止。

二、算法的计算流程

算例及仿真

某实际配电网络的接线图见图2。线路参数和负荷数据见表1。

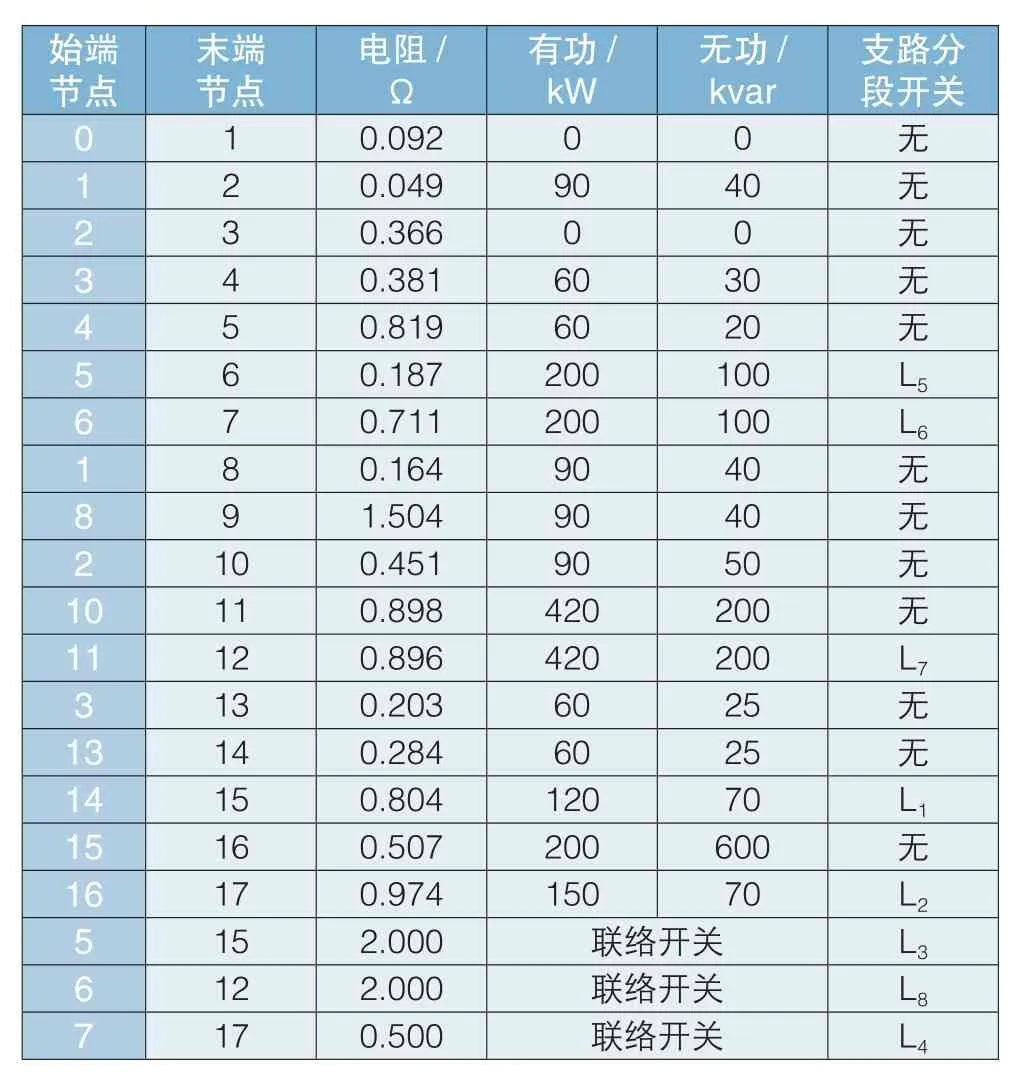
表1　节点的配电系统数据

其中根节点0为平衡节点（电压值为10.5kV，相角为0°），L为联络开关。利用改进的蚁群最优恢复重构算法对2个操作集中各自应分段的支路进行搜索，同时注意公共支路的处理问题，从而得到其最优恢复重构方案。首先初始化“信息素”C0＝1.0，最大迭代次数Nmax＝20，蚁群数量m＝5，“信息素”蒸发系数ρ＝0.9，常量Q＝1.0。然后根据上述所介绍的算法对其进行迭代搜索最优方案。

用本文所介绍的改进的蚁群最优故障恢复重构算法和遗传算法（GA）、支路交换法（BEM），可以将对配电网络图2所包含的数据进行带入运行运行之后得到的仿真图像如下图3所示。

根据上述的结果可以看出，改进后的蚁群最优算法相对于启发式的支路交换算法的优点是其具有更少的迭代次数，缺点是收敛至全局最优解的次数较大和收敛耗时较大；而其相对于遗传算法来说，其优点是迭代次数少和收敛耗时小，缺点是收敛至全局最优解的次数较大。因此，利用改进蚁群最优算法来解决故障恢复问题具有更少的迭代次数，耗时较小，应用在实际电力系统过程中，其收敛至全局最优解的次数少，其内存更小、实时性更强、全局稳定性更好。

结束语

在配电网故障恢复重构问题的研发中，由于所学知识领域的限制，仅研发了适用于大电力系统运行状态下配电网管理系统，在后期条件允许的情况下，可以进一步加上分布式发电，重要是风力发电、太阳能发电等一些不稳定的分布式电源并网问题的电力系统。除了应用目前的算法来解决问题之外，之后还可以结合以前常规的计算分析方法和智能控制部分对配电网故障恢复重构进行进一步的研究。

（作者单位：肖惜明，贾铁军，张福杰：上海电机学院；刘文文：枣庄电信分公司）