基于小波变换的声雷达模拟信号去噪研究

郭凤霞，戚 俊，陈斐楠，吕祚坤，江世海，李 燕，叶荣辉，龚大伟

(中国科学院合肥物质科学研究院应用技术研究所, 合肥 230088)



·仿真技术·

基于小波变换的声雷达模拟信号去噪研究

郭凤霞，戚 俊，陈斐楠，吕祚坤，江世海，李 燕，叶荣辉，龚大伟

(中国科学院合肥物质科学研究院应用技术研究所, 合肥 230088)

雷达信号模拟和信号处理技术对雷达系统研制具有重要的意义。文中分析了描述回波幅度和功率谱分布的统计模型，并深入研究了幅度服从一定分布同时具有特定功率谱的声雷达回波信号的建模与仿真方法，实现了声雷达探测大气回波信号的模拟。基于小波变换理论对回波信号进行了去噪方法研究。利用MATLAB仿真对各种影响小波去噪性能的参数进行了比较，确定将db20小波用于声雷达回波信号去噪处理。并通过对比试验得到适用于回波信号的最佳分解层数和阈值，实现了声雷达回波信号中杂波和噪声的去除，仿真结果验证了文中方法的有效性。

风廓线声雷达；幅度分布；功率谱分布；小波变换；阈值函数

0 引 言

多普勒声雷达是一种基于大气湍流对声波的散射作用实现对流层低层大气结构和风场等物理量探测的主动大气遥感装备，可广泛应用在大气边界层气象研究、污染天气监测、风电场复杂地形测风和大气环境评价等方面，其提供的低层三维风场结构适用于对空气污染气象背景的监测和预测；可以捕获详细的边界层现象，如夜间低空急流，边界层白天的对流结构以及高空逆温现象；还可以为湍流建模领域提供大气边界层湍流结构的信息等。

声雷达的应用也存在一定的局限性，例如由于噪音污染使其不能应用于人口密集地区，地面的非均质性会影响声雷达的测量结果等。并且在研制过程中由于开发环境及实验条件的限制，使得声雷达模拟技术对于声雷达系统的设计、分析以及调试具有特别重要的意义。雷达模拟技术可以模拟雷达各种工作环境，从而缩短雷达的研制周期，减少雷达的研制费用，同时也方便信号的理论研究。近年来，大气遥感领域扫描技术的模拟在雷达气象领域取得了一定的成就，如：天气雷达[1]、毫米波云雷达、边界层风廓线雷达[2]等；Charlotte E W[3]等进行了基于大涡模拟的声雷达模拟器的研究。

本文对声雷达回波信号的模拟技术进行了探索和研究，分析了描述回波幅度和功率谱分布的统计模型，并深入研究了声雷达大气回波信号、噪声和杂波信号的建模与仿真方法，分别模拟出幅度服从一定分布并具有特定功率谱的大气回波信号、噪声以及杂波信号的随机序列；利用小波变换理论对受噪声和杂波污染的大气回波信号进行了去噪方法的研究，实现了在杂波和强噪声干扰下的声雷达回波信号中杂波和噪声去除。研究结果对声雷达的使用和研制具有一定的科学意义和参考价值，对声雷达技术的发展也具有极其重要的意义。

1 声雷达回波信号模拟

风廓线声雷达信号包括大气湍流的散射回波、均匀背景噪声、地物杂波和间歇性杂波。雷达模拟的核心就是建立雷达大气回波信号及各种杂波信号散射、传播特性的模型。

1.1 大气回波模型

来自声雷达散射体的信号和散射波接收的功率强度，可近似地由下列雷达方程表示

(1)

式中：C为散射体内的平均声速；τp为脉冲宽度；σs为距离R处的后向散射截面；PR为接收信号的电功率；Pt为发射信号的电功率；E为电声-声电转换效率；α(r)为距离r处的大气声波衰减系数；A为天线有效面积；G为天线有效面积系数；R为到达散射体的距离。在局地均匀各向同性湍流后向散射中，声波散射截面为[4]

(2)

根据雷达方程可以求出一定条件下雷达回波信号的功率大小。当检测范围内目标信号数目不止一个并且它们的信号相互之间存在一定关系时，就要考虑它们之间的相位关系。单个散射体的反射信号的相位为[3]

Φ=exp[-j2π(fT+fs)t]

(3)

式中：fT为发射信号载频；fs为散射体与雷达的相对运动引起的多普勒频率。

(4)

式中：vr为散射体相对雷达的径向速度。包含散射体振幅和相位信息的接收信号的表达式为

(5)

通过对来自单个散射体，既包括幅度信息又包含相位信息的接收信号进行模拟，再对信号采用相干求和的方法，就可以模拟来自多个散射体的合成信号。由于大气回波信号的复杂性和多样性，通常采用一些比较接近而又合理的统计模型进行分析，大气回波信号模拟也就等于模拟具有特定的幅度概率密度和功率谱密度的随机过程。本文拟产生幅度分布服从瑞利分布，功率谱满足高斯谱模型的随机序列来模拟大气回波信号，如图1所示。

1.2 杂波信号建模

杂波信号是由大气湍流之外的物体，通常为桅杆、树木、建筑物等环境物体反射回来的回波。雷达杂波是来自雷达分辨单元内的许多散射体回波的矢量和，由于雷达分辨单元内一般包括许多随机分布的散射体，而每一部分反射回来的回波，其振幅和相位都是随机的，通常用杂波幅度的概率分布模型和杂波相关模型来描述。目前常用的幅度分布模型有：瑞利分布、对数正态分布、韦布尔分布、K分布等[5]，其中瑞利分布是雷达杂波中最常用也是用的最早的一种统计模型，可以描述气象杂波、海杂波、地物杂波等。常用的谱模型有两种：高斯谱和平方谱模型。大量的测试结果及理论分析表明，大多数杂波功率谱展宽可用高斯曲线来逼近。因此，本文拟产生幅度分布服从瑞利分布，功率谱满足高斯谱模型的随机序列来模拟雷达杂波信号，如图2所示。从时域上看，地杂波相对于湍流回波信号变化较为缓慢，具有较大振幅并有较长的相关时间[6]。

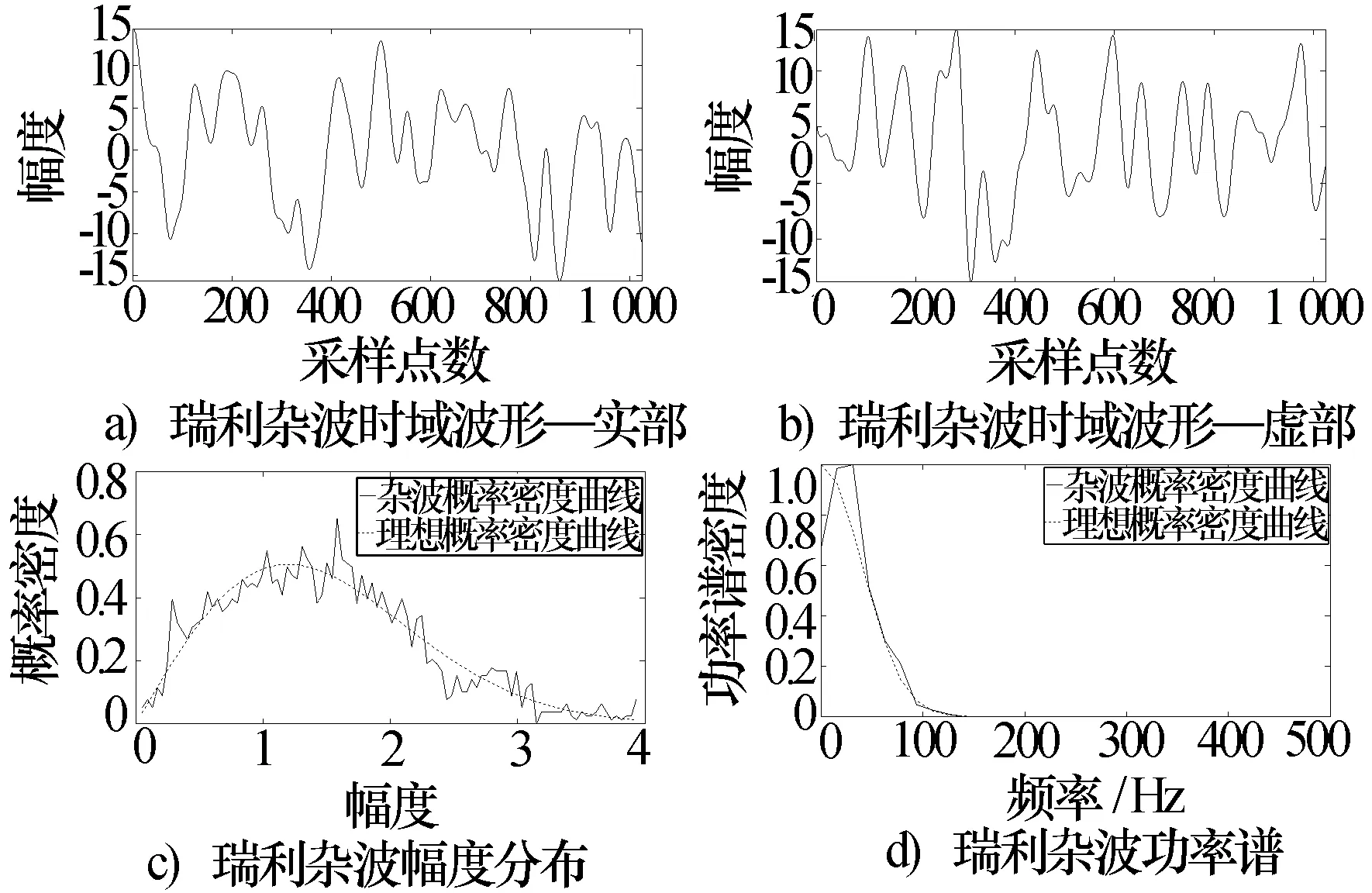
图2 瑞利分布杂波仿真序列

1.3 噪声信号模拟

雷达回波信号的噪声来源主要是环境背景噪声和内部噪声，通常用分布模型和信噪比来描述噪声。内部噪声主要由接收机中的馈线、放电保护器、高频放大器等产生。一般情况下，回波中的内部噪声看作是高斯白噪声。外部噪声是由雷达天线进入接收机的各种人为干扰和工业干扰等，来源包括机械设备如发电机、公路运输、重型机械、飞机以及昆虫鸟类等。其中的某些噪声源产生的宽带信号和声雷达频带宽度重叠，降低了声雷达的信噪比，从而降低了声雷达所能探测的最大距离[7]。Bradley[8]给出环境背景噪声为粉红噪声，从功率(能量)的角度来看，其能量从低频向高频不断衰减，曲线为1/f。图3、图4分别给出了为模拟得到的高斯白噪声和粉红噪声的时间序列及其频谱。

图3 高斯白噪声仿真序列及其频谱

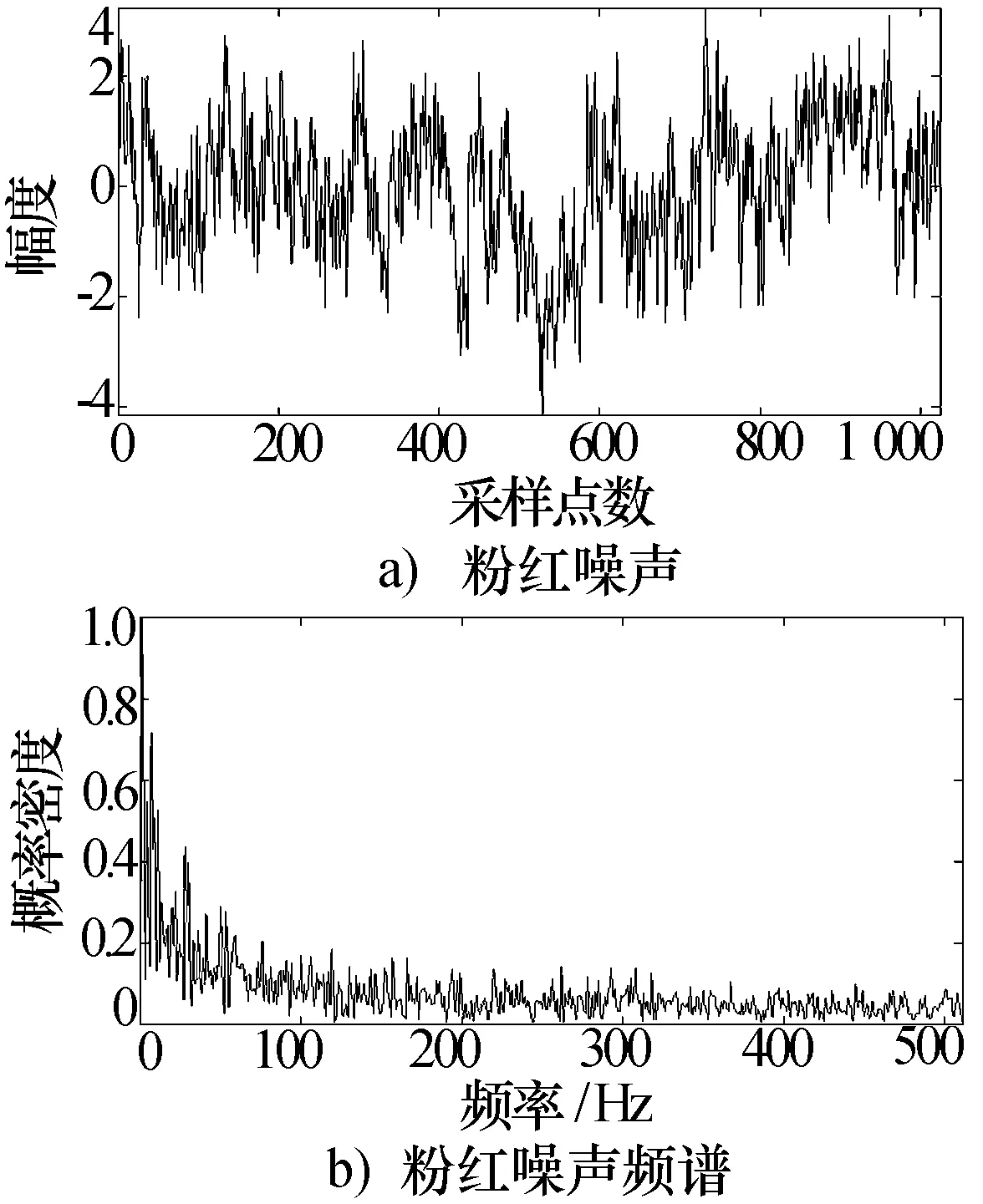
图4 粉红噪声仿真序列及其频谱

1.4 风廓线声雷达回波信号合成

将大气回波信号、杂波信号和噪声合成为声雷达探测大气回波信号，其中信噪比为0，杂信比为15，如图5所示，由于杂波信号具有较强振幅，风廓线声雷达的大气回波信号已经完全被其掩盖，此时信号的特征主要表现为杂波的特征。

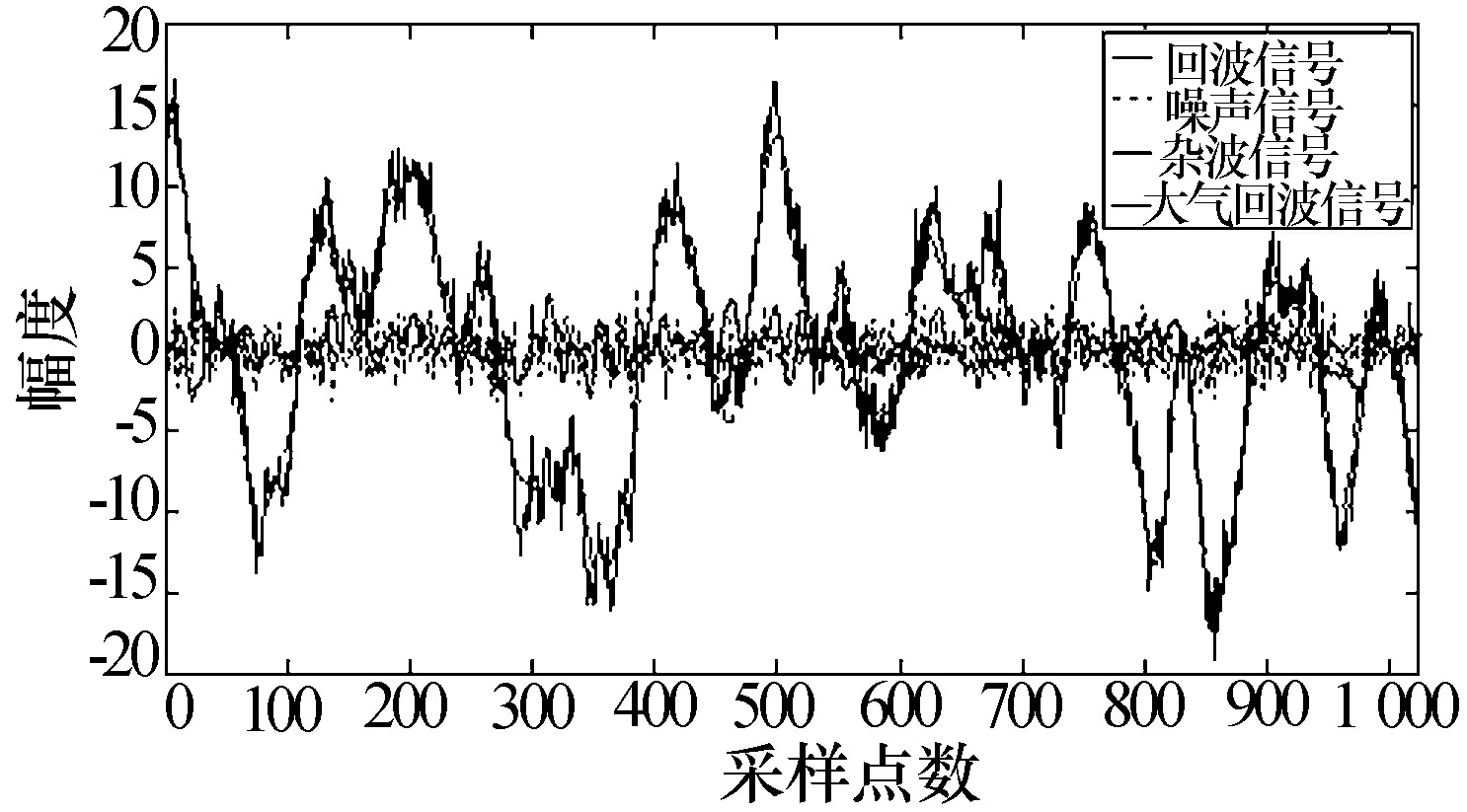
图5 声雷达探测大气回波信号

2 小波变换

小波变换是一种新型的信号处理方法，具有平移、伸缩的特性，在时、频两域同时具有良好的局部化特点，可以由粗及细地逐步观察信号，适合分析非平稳信号。下面简单介绍小波函数的概念及小波变换去噪的基本原理。

给定一个基本函数Ψ(t)，令

(6)

式中：若a,b不断地变化，可以得到一族函数Ψa,b(t)。给定平方可积的信号f(t)，即f(t)∈L2(R)，则f(t)的小波变化(WT)定义为

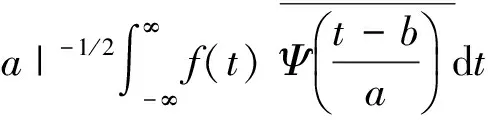
a≠0

(7)

式中：b是时移因子；a是尺度因子；Ψ(t)称为基本小波，或母小波；Ψa,b(t)是母小波经移位和伸缩产生的一族函数，称之为小波基函数，或简称小波基。

3 杂波及噪声抑制算法实现

针对本文所模拟得到的声雷达回波信号的杂波和噪声的去除，主要经过两个步骤：首先，根据杂波和大气回波信号小波变换系数的不同特征，去除含有杂波成分的小波变换系数；然后，根据大气回波信号和噪声的不同特点，去除回波信号中的噪声成分。

目前，阈值去噪方法由于简单有效且易于实现，成为众多小波变换去噪方法中研究最为广泛的方法[9]。由于传统的软阈值或硬阈值处理方法本身存在的一些不足，因此很多文献对软、硬阈值去噪方法作出了一定的改进，在硬阈值函数和软阈值函数之间作一个折中，并对阈值的选取作出一定的改进。本文选用一种半软阈值函数[10]，有效地去除了杂波和噪声，提高了重构信号的信噪比，且保留了原始信号的细节特征。

进行小波变换去噪的第一步是要选择适用于研究信号的小波基函数和最佳分解层数。小波基函数的选择主要考虑两点：光滑性和相似性。本文分别采用Matlab中提供的Symlets、Daubechies、Coiflet和Biorthogonal四种离散小波系来进行多次检验，根据各种小波处理信号的实际效果来确定适合声雷达回波信号的小波基函数。小波基函数确定后，输入相同信号，对采用不同分解层数的重构波形进行比较，即可确定最佳小波基下的最佳分解层数。

对于上述模拟的声雷达回波信号，通过Matlab大量仿真试验对比发现：db20由于具有平滑和慢变的特点，和杂波信号具有较强的相似性，相比其他小波函数，重构信号具有较高的信噪比。因此，本文选择db20小波对声雷达回波信号进行去除杂波处理，通过仿真试验对比得到最佳分解层数为4，可以保证杂波信号能量集中在最低层的低频系数上，最大程度地将杂波信号和有用回波信号分解在不同的层次上，有利于后续的处理。对去除杂波后含有噪声的大气回波信号同样经过上述检验，得到噪声抑制的最佳小波基函数为db20，最佳分解层数为3，其中低频部分和大尺度的高频部分含大气回波信息比较多，而第一个尺度高频部分就以噪声为主。图6分别给出大气回波信号、杂波信号、噪声及合成回波信号经db20小波变换的系数，可以看出，白噪声的能量分散于大量的小波系数上，分解后的白噪声的小波系数仍是白噪声，幅度分布比较平均，且最大幅度不超过5。而大气回波信号的小波系数分布在较小的范围内，并且对应分解层数的不同，小波系数的幅度具有明显的变化，其最大幅度在11之内。杂波的小波系数分布在更小的范围内，在不同的分解层数下，小波系数的幅度具有更为明显的变化，由于杂波信号强度比大气回波信号和噪声强很多，其小波分解后系数值也大很多，其最大幅度达到近70。根据各种信号在小波域的不同表现特征，选择合适的阈值进行滤波，可以有效的将杂波和噪声信号去除。

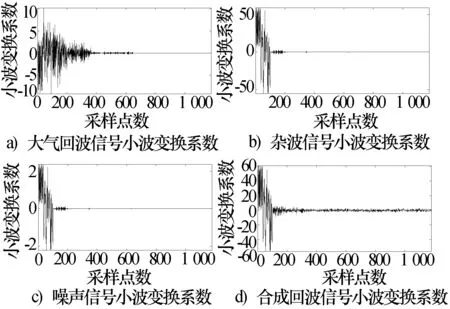
图6 各种信号db20小波变换系数

将小波域中确定为杂波成分的较大系数予以截取，可以去除回波信号中的杂波。对于截取阈值的选取，传统的做法是选取后一半小波系数的最大值作为截取阈值[6]，但其存在以下潜在的缺点：阈值可能会过小而使得有用回波信号也被滤除，阈值可能会过大而保留过多的杂波信号。这里首先采用3σ准则，去除最邻近低频信号的高频系数中的“粗差”信号，然后选择该层高频系数的最高值作为阈值。该方法成立的基础是认为经过上述小波变换的处理，将杂波信号和回波信号分解在不同的小波层次上，杂波信号绝大部分存在于低频信号中，因此主要针对小波变换的低频系数进行处理就可以很好地滤除杂波信号。但在高频层次上不可避免的仍然存在一定数量的杂波信号，残余杂波的去除是下一步研究的重点。图7给出杂波去除前后的对比结果，并与大气回波信号和噪声的合成信号进行比较，二者比较接近，重构效果较好。

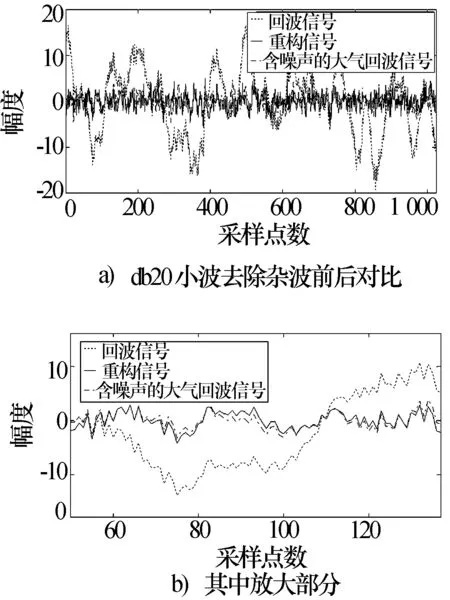
图7 杂波去除前后对比图

去除杂波信号的回波信号中仍然含有噪声信号，下一步是对高斯白噪声进行去噪。本文采用3σ准则，提取每层的阈值，其具体流程见文献[11]。3σ准则主要是根据高斯噪声的分布特点来考虑的，若高斯分布的噪声均方值为σ，则根据其分布规律，瞬时值绝对值大于3σ的概率仅为3%，认为其是粗大误差。对大气回波信号与高斯噪声的迭加信号进行小波变换，噪声在每层高频系数中仍是服从高斯分布的随机序列，而大气回波信号的突变部分在小波的高频分解系数中表现为一系列脉冲。因此，可将大气回波信号的突变部分在小波分解系数中的表现看作“粗差”，而噪声的小波分解系数仍是高斯“误差”，从而运用3σ准则检测出大气回波信号分量。然后，利用半软阈值函数[9]对每层高频系数进行阈值处理，处理后的高频系数和低频系数进行重构，得到去噪信号。去噪效果如图8所示，与模拟的大气回波信号相比，不仅二者吻合效果较好，而且用最小均方误差和信噪比这两种评价指标进行客观评价，也获得满意的效果。例如，在干燥天气下，声雷达探测大气回波信号信噪比为0 dB，经以上小波变换方法去噪后增加为7 dB以上。

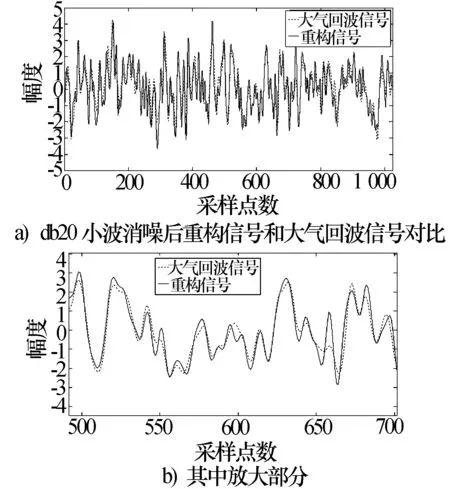
图8 去噪后重构信号和大气回波信号对比图

4 结束语

本文基于多普勒声雷达信号的基本原理和相关参数特性，以Matlab软件作为信号仿真工具，对声雷达探测大气的回波信号进行了理论分析和仿真验证研究。讨论了大气回波信号的数学模型及杂波统计建模方法，给出同时具有特定幅度概率密度和功率谱密度的随机序列的模拟方法，并通过仿真验证了方法的有效性。此外，分析了声雷达回波信号的噪声来源和类别，介绍了噪声建模的方法。最后，对上述各模拟信号进行合成得到声雷达探测大气模拟回波信号。

模拟得到的声雷达回波信号中杂波和噪声的去除需要经过两个步骤：首先，根据杂波和大气回波信号小波变换系数的不同特征，去除含有杂波成分的小波变换系数；然后，根据大气回波信号和噪声的不同特点，去除回波信号中的噪声成分。采用一种半软阈值函数，结合3σ准则，有效的去除了高斯白噪声，从低信噪比回波信号中恢复大气回波信号波形，提高了重构信号的信噪比，保留了原始信号的细节特征。

[1] MAY R M, BIGGERSTAFF M I, XUE M. A Doppler radar emulator with an application to the detectability of tornadic signatures[J]. Journal of Atmospheric and Oceanic Technology, 2007, 24(12): 1973-1996.

[3] WAINWRIGHT C E, STERANIAN P M, CHILSON P B, et al. A time series sodar simulator based on large-eddy simulation[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31(4): 876-889.

[4] LITTLE C G. Acoustic methods for the remote probing of the lower atmosphere[J]. Proceedings of the IEEE, 1969, 57(4): 571-578.

[5] 赵 翠，江朝抒，马 静，等. 基于ZMNL的相关广义复合分布雷达海杂波仿真[J]. 现代雷达，2015, 37(2): 75-78. ZHAO Cui, JIANG Chaoshu, MA Jing, et al. Simulation of correlated generalized-compound-distributed radar sea clutter based on ZMNL transformation[J]. Modern Radar, 2015, 37(2): 75-78.

[6] JORDAN J R，LATAITIS R J，CARTER D A. Removing ground and intermittent clutter contamination from wind profiler signals using wavelet transforms[J]. Journal of Atmospheric and Oceanic Technology, 1997, 14(6): 1280-1297.

[7] CRESCENTI G H. The degradation of doppler sodar performance due to noise: a review[J]. Atmospheric Environment, 1998, 32(9): 1499-1509.

[8] BRADLEY S. The noise part of sodar signal-to-noise[C]//Extended Abstracts of Presentations from the 16th International Symposium for the Advancement of Boundary-Layer Remote Sensing. Boulder, Colorado:[S.l.], 2012: 271-274.

[9] 赵红怡. 基于小波变换阈值的信号去噪[J]. 现代雷达，2001, 23(2): 37-39. ZHAO Hongyi. Wavelet transform application for signal denoising[J]. Modern Radar, 2001, 23(2): 37-39.

[10] SANAM T F, SHAHNAZ C. A semisoft thresholding method based on teager energy operation on wavelet packet coefficients for enhancing noisy speech[J]. EURASIP Journal on Audio, Speech, and Music Processing, 2013(25): 1-15.

[11] 张秀秀，赵 薇，李 封，等. 3σ准则在心电信号小波消噪处理中的应用[J]. 机械设计与制造，2006(11)：107-109. ZHANG Xiuxiu, ZHAO Wei, LI Feng, et al. Application of de-noising of ECG signal based on wavelet transform of 3σrule[J]. Machinery Design & Manufacture, 2006(11): 107-109.

郭凤霞 女，1980年生，工程师。研究方向为光电检测仪器测量原理及核心算法。

戚 俊 男，1971年生，博士，研究员。研究方向为光电测控。

陈斐楠 男，1986年生，博士，助理研究员。研究方向为大气光学检测。

吕祚坤 男，1986年生，硕士，助理工程师。研究方向为信号处理与信号传输。

A Study on Noise Suppression Methods for Sodar Analog Signals Based on Wavelet Transform

GUO Fengxia，QI Jun，CHEN Feinan，LV Zuokun，JIANG Shihai，LI Yan，YE Ronghui，GONG Dawei

(Institute of Applied Technology, Heifei Institute of Physical Science,Chinese Academy of Sciences, Heifei 230088, China)

It is practically significant of radar signal simulation and signal processing technology for radar invention．The simulated echo signal of sodar for detecting atmosphere was produced based on the statistical model and the method of modeling and simulation for atmosphere return signal, noise and clutter that meet certain amplitude and power spectrum. Wavelet denoising methods was carried out on echo signal polluted by clutter and noise so that to ensure the sodar signal processing ability. The db20 wavelet proved best scheme of wavelet denoising for sodar echo signal, simulated by MATLAB, various parameters that influence the performance of wavelet denoising were studied. The comparison experiments showed the optimal wavelet decomposition level and the appropriate threshold. The simulation results achieved reducing the clutter and noise from sodar echo signal, validated the proposed method.

wind profiler sodar; amplitude distribution; power spectrum distribution; wavelet transform; threshold function

10.16592/ j.cnki.1004-7859.2016.03.018

中国科学院合肥物质科学研究院院长基金资助项目(YZJJ201330)

郭凤霞 Email：fxguo@rntek.cas.cn

2015-10-13

2015-12-15

TN957

A

1004-7859(2016)03-0086-05