低速轴流涡轮叶片层流分离流动的数值模拟方法比较*

王晓东 刘晓杰 梁丽萍 康顺/华北电力大学能源动力与机械工程学院

低速轴流涡轮叶片层流分离流动的数值模拟方法比较*

王晓东 刘晓杰 梁丽萍 康顺/华北电力大学能源动力与机械工程学院

0 引言

叶轮机械内部流动本质上是复杂的三维粘性非定常流动。低速涡轮内流动可能涉及到流态的转变、层流分离和显著的径向二次流动[1]，其内部流动更为复杂。小型燃气轮机的低速涡轮进口雷诺数可能低至25 000，远低于大型燃气轮机低速涡轮的进口雷诺数[2]。低雷诺数进口条件使得低速涡轮偏离设计点工况，其气动性能严重下降。因此，研究低速涡轮内部的分离流动和二次流，尤其是在低雷诺数进口条件下的流动，具有重要意义。

目前，国内外对高转速涡轮内部流动的研究较多，但是对低转速涡轮内三维流动细节研究相对较少。在低进口雷诺数下，叶片通道内大部分区域保持层流。Treuren等[3]研究了进口雷诺数在25 000～50 000的叶栅内部流动。发现在低雷诺数下，进口湍流度在1％时，叶片吸力面发生大的分离，但分离流动是稳定的。提高进口湍流度到8％左右，分离流动变的不稳定。在较高雷诺数下，即使进口湍流度很低，分离流动也不稳定。Bernardini等[4]在低速叶栅实验中发现当雷诺数在25 000～75 000的范围内时叶栅吸力面表面产生的分离泡很薄。当雷诺数低至20 000时，分离泡会延伸至尾缘下游而不再附于叶片表面。Matsunuma[5]对某低速轴流涡轮内部流场进行了细致的实验研究，详细分析了在低雷诺数进口条件下静动叶通道内的流动细节，发现静叶通道内边界层主要为层流边界层，静叶吸力面发生层流分离，分离流有很大的径向运动。Schobeiri等[6]采用人工尾迹的方法研究了低速涡轮叶栅在不同雷诺数下的边界层发展、转捩和分离的过程。提高叶栅进口的湍流度和雷诺数有助于减小叶片吸力面的分离区。Mahallati和Sjolander[7]采用类似的模型研究了更低雷诺数下涡轮叶栅内部流动。研究发现来流尾迹对叶片流动分离的抑制作用很有限，但是转捩可以使分离流提前再附。Maclsaac等[8]通过实验测得了某低速涡轮平面叶栅下游的时均流场和湍流流场，详细阐述了叶栅下游二次流损失形成的机理，并指出准确模拟湍流脉动是准确计算叶栅总压损失的关键。Reinaldo等[9]采用实验研究了低速涡轮平面叶栅的叶片表面层流分离引起的Bypass转捩，并与采用转捩模型的数值模拟进行了比较。结果显示数值模拟难以正确捕捉转捩的初始扰动，转捩区域较小。

根据以上的研究结论可知，低速涡轮在低雷诺数进口条件下的主要流动特征是层流分离和转捩流动，而当前数值模拟对于同时捕捉层流分离和转捩较为困难。本文以文献[5]中的低速轴流涡轮为研究对象，分别采用全层流模型、全湍流模型、AGS转捩模型和DES方法，研究了低速涡轮级静叶片通道内的流动结构。

1 计算模型

本文研究的模型基于文献[5]的单级轴流低速涡轮。静叶和动叶叶片数分别为28和31，动叶转速为402r/min。静叶和动叶叶高H分别为75mm和74mm，叶顶间隙为1mm。叶片采用自由涡方法生成，动叶顶部有较大的进口负攻角，根部有较大的正攻角。动叶的折转角较大，其出口气流角约60°。涡轮的几何参数可以参考文献[5]。

文献[5]在低速回流式风洞试验台对该涡轮进行了实验研究。试验段进口的湍流强度为0.5％，进口气流角为0°，进口平均速度为4.7m/s。以静叶弦长和进口速度定义的雷诺数为20 000。以静叶出口速度定义的雷诺数为47 900；而以动叶弦长和动叶出口速度定义的雷诺数为35 000。由此可见，此实验中，该涡轮工作在非常低的雷诺数下。

静叶通道进出口的绝对马赫数分别为0.013和0.031，动叶通道进出口的相对马赫数分别为0.014和0.027，均远小于0.3，因此本文采用了不可压缩工质。

2 计算方法及边界条件

计算域及网格：计算域进口设置在静叶前缘上游30mm处，即ZST/Cax,ST=-0.706，其中Z表示轴向距离，下标ST表示静子，Cax表示轴向弦长。出口设置在动叶叶中尾缘下游3倍轴向弦长处。采用AutoGrid软件生成单通道多块贴体结构网格。为验证网格无关性，共生成了网格总数从134万至1 088万共7套网格，详见文献[6]。图1给出了网格总数约213万的计算域和网格图，其中叶顶间隙内网格总数约为4.5万。静叶网格点数为89×161×65（周向×轴向×展向），动叶网格点数为121×137×65（周向×轴向×展向），间隙内展向网格点数为9。静叶近壁面y+值小于0.6，动叶近壁面y+值小于1.6。

图1 计算网格

边界条件：进口给定总温300K，及速度沿径向的分布。进口位移边界层在叶顶的厚度为1.85mm，叶根的厚度为1.68mm，形状因子约为2.3，接近层流边界层的形状因子。出口给定静压110kPa。通道两侧为非匹配连接的周期性边界，转静子交接面采用完全非匹配连接的一维无反射边界，采用混合平面法处理。端壁及叶片表面为绝热无滑移固壁。

根据文献[5]，静叶通道内的边界层主要为层流边界层。而由于静叶尾缘与动叶前缘的干涉作用，动叶通道内边界层主要为湍流边界层。因此一个自然的想法是静叶内采用层流模拟，动叶内采用湍流模拟。因此，采用FINE/Turbo软件包在静叶通道内进行了层流方程的求解，动叶通道内仍采用全湍流模型，Spalart-Allmaras一方程湍流模型。该模型被广泛应用于叶轮机械数值模拟中，被证实具有极高的可信性[10-11]。不可压缩流动采用了Merkle低速预处理方法[12]。为了加以对比，同时进行了静叶内采用全湍流模型和AGS转捩模型[13]的模拟。

计算时选用了二阶精度的中心离散格式，时间离散采用四阶Runge-Kutta法，并采用了全多重网格初场处理，以及多重网格迭代加速收敛。残差收敛到10e-5～10e-6的量阶。

3 计算结果与分析

图2给出了采用7套网格计算的绝热效率。由图可见网格1与其他网格计算结果差距较大，网格2与网格7的之间的误差约为2.7％。网格6和网格7的差别非常小，仅为0.12％。图3给出了静叶出口下游15.4％弦长处周向平均的总压损失系数沿径向的分布。由该图可以看到各网格计算结果差别很小，在大部分范围内与实验结果贴合很好，仅在80％叶高附近和根部10％叶高附近计算的总压损失均较实验值偏小。考虑到网格6, 7的计算量很大，网格2计算量较小，且其与网格7的误差也不大，因此本文后继计算主要采用网格2。

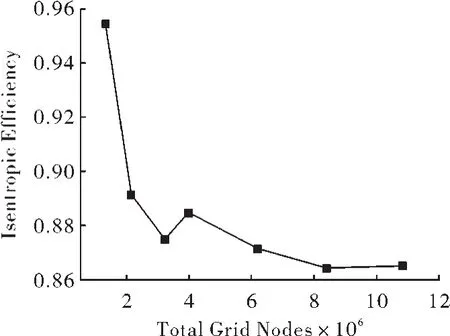
图2 不同密度网格计算的绝热效率曲线图

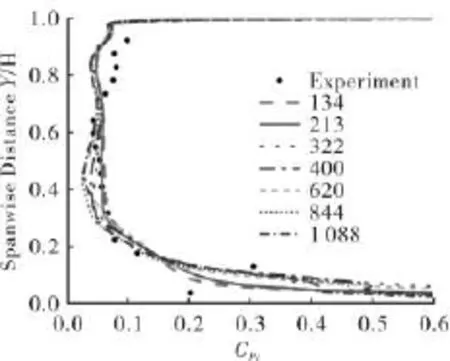
图3 静叶下游周向平均的总压损失系数分布图

图4和图5对比了油流实验与数值模拟得到的静叶吸力面表面的流谱。为了对比层流模拟和全湍流模拟结果的不同，同时给出了静叶通道分别采用全湍流模拟和采用AGS转捩模型的模拟结果。根据图4的实验结果，静叶吸力面表面的流动主要分为A，B，C，D四个区域。靠近静叶前缘的区域A是低雷诺数进口条件下在静叶表面形成的层流边界层区。之后受逆压梯度作用，边界层发生分离，形成层流边界层分离区，为区域B。靠近静叶尾缘存在一个回流区C。在静叶根部和顶部还存在明显的通道涡区域。在尾缘根部附近，根部通道涡与回流区相互掺混形成混流区D。

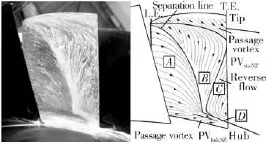
图4 静叶吸力面油流实验图[5]

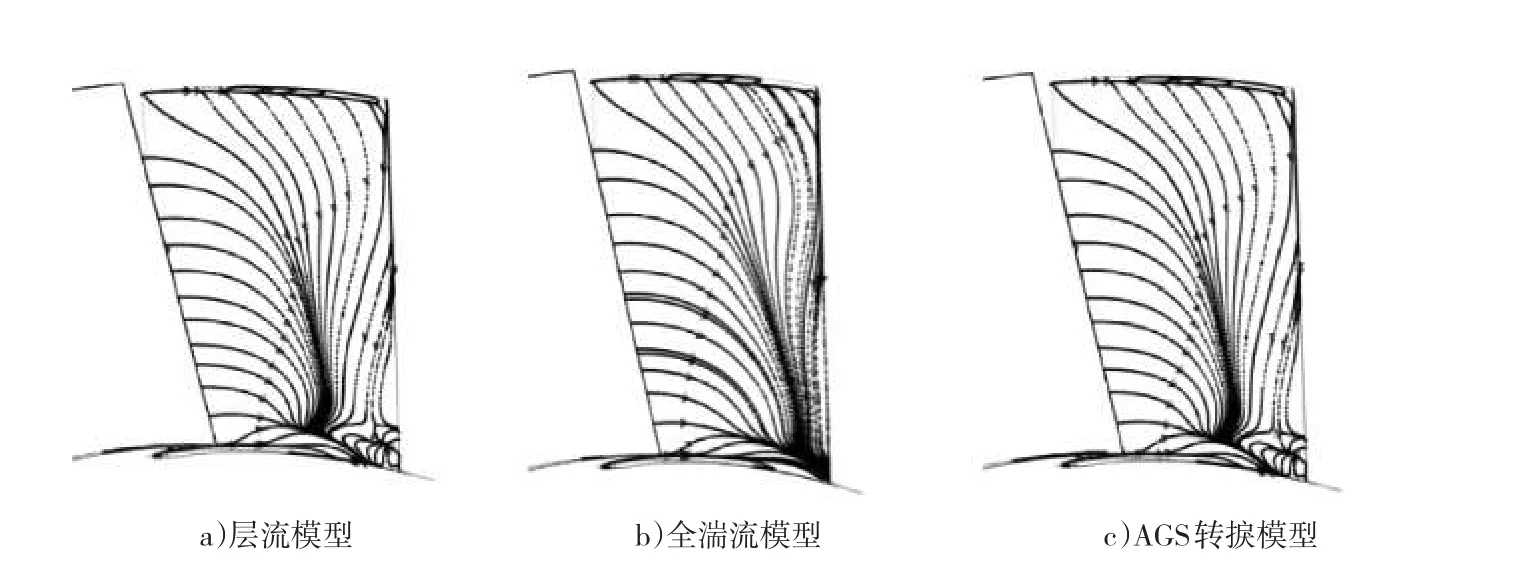
图5 静叶吸力面极限流线图谱

从图5的模拟结果来看，采用层流和AGS转捩两种模拟方法的模拟结果基本相同，均与油流实验得到的结果高度相似，准确地捕捉到了层流边界层区、分离区、回流区、混流区和根部通道涡区域，达到了良好的模拟效果，由此可以推断，边界层转捩应该发生在层流分离之后。全湍流模拟结果相较于油流实验，分离线明显后移，向叶片尾缘靠近，分离延迟。无明显的回流区和壁角处混流区。由以上对比分析可以确认，在静叶吸力面表面流体转捩之前发生了层流分离，并在分离区内实现转捩。静叶通道求解层流方程能够很好地捕捉到静叶表面层流分离的位置，最准确地模拟出叶片表面的流动状况。但是，采用全层流的模拟方法没有观察到顶部通道涡，其他两种方法模拟得到的顶部通道涡区域的范围也均小于实验结果。

图6展示了静叶下游1.154倍轴向弦长截面处绝对速度分布的模拟结果与文献[5]的实验结果进行对比，并用静叶出口平均速度进行无量纲化。由于采用AGS模型与层流模型得到的结果基本相同，图中只给出了层流模拟结果。与图5结论一致，采用层流模拟与实验结果大部分区域吻合良好，仅轮毂处的边界层厚度比实验结果偏大。尾迹和二次涡流在静叶尾缘下游形成了一条从根至顶的狭长低速带。其中，根部通道涡强度较大，能够观察到明显的低速核心区；而顶部通道涡受分离流的影响大幅拉伸，没有形成集中的涡核，强度较弱。由于层流对于通道涡引起的速度亏损模拟不足。因此，在根部通道涡位置处层流模拟的速度略大于实验值和湍流模拟结果。由以上分析可知，层流模型可以准确捕捉静叶吸力面的层流分离，但是对于分离后的湍流和通道涡等二次流引起的速度亏损和总压损失模拟不足。因此本文考虑采用分离涡模拟（DES）方法进行模拟。由于进行整级的分离涡模拟需要生成全周网格，计算量很大。因此，仅对静叶进行分离涡模拟。静叶单通道网格数为149万，计算域进口条件与前述条件一致。出口压力根据实验结果给定转静交界面处压力。

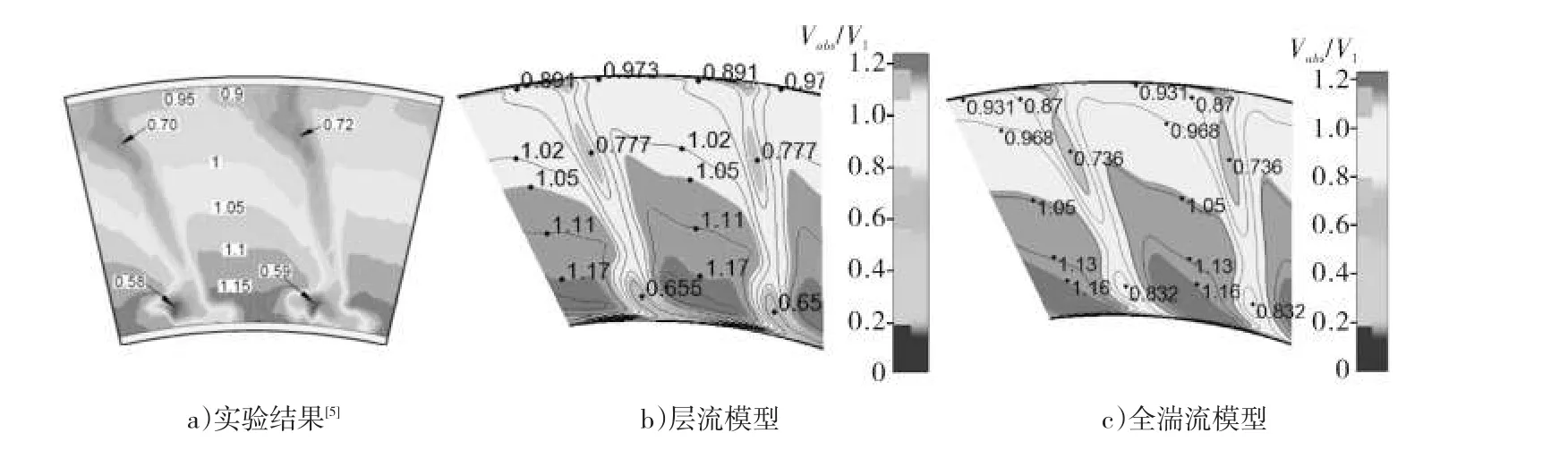
图6 静叶尾缘下游截面速度分布云图

图7给出了DES模拟获得的静叶下游1.154倍轴向弦长处截面的绝对速度云图。与图6相比，DES的结果更接近实验结果。根部通道涡沿周向的拉伸更为明显。叶顶的通道涡也比层流和全湍流模拟结果更为明显。

图8和图9分别给出了静叶下游1.154倍轴向弦长处截面周向平均的绝对总压损失和绝对速度沿展向分布与实验结果的对比。各模拟结果与实验值的分布趋势一致。

图7 分离涡模拟的静叶下游截面速度分布云图

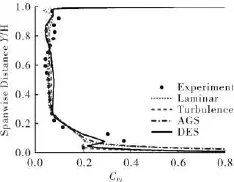
图8 静叶总压损失系数沿径向分布图

图9 静叶下游绝对速度沿径向分布图

分析实验值并结合云图可知，由于根部通道涡的存在，13％叶高附近总压损失显著增加，速度发生大幅亏损。靠近叶片顶部还存在较大范围的不明显的速度亏损，这是由静叶顶部通道涡引起的。受径向强压力梯度作用顶部通道涡沿展向拉伸，没有形成集中的涡核，其特点是尺度大。采用层流和AGS转捩模拟得到的结果几乎重合。采用全湍流模拟，轮毂处边界层与实验值贴合较好。采用DES模拟比其他方法更好地捕捉到了根部速度亏损和总压损失，并精确计算出轮毂壁面边界层厚度约为3％。全湍流模拟计算的轮毂边界层厚度也较为准确，其他方法模拟出的边界层较厚。采用全湍流模拟得到了根部速度亏损的趋势，但是由于其预估的边界层分离推迟，使得模拟得到的速度偏大。因此，在叶中位置处，DES模拟的总压损失较其他结果稍偏大，而全湍流模拟的总压损失又略大于层流模拟和AGS模拟。

图10给出了层流模拟获得的静叶通道内三维空间流线图与沿流向分布的8个截面绝对速度分布云图。截面1位于静叶前缘位置，截面2至截面7分别位于前一截面下游的10％弦长。截面8位于转静交界面。截面1上主流区的速度近似为均匀分布，靠近叶根和叶顶的低速区为上下端壁发展的边界层。在截面2,3和截面4，速度在吸力面侧加速。在截面5，在叶片表面附近观察到两个小的分离区，分别对应与根部通道涡和顶部通道涡。截面6，靠近叶顶的分离区迅速增大，并沿径向延伸。在截面7上，上下分离区相接。截面8上速度分布与图6相似，一条狭窄的尾迹区形成三个低速带，分布对应叶顶通道涡叶根通道涡和分离流。根据文献[14]提出的涡轮内部二次流模型，压力面侧的马蹄涡分支离开前缘后在周向压力梯度作用下向相邻叶片的吸力侧运动，并在主流的携带下与来流边界层形成一个多涡系统。该多涡系统到达相邻叶片吸力面的大约1/4弧长处与吸力面的马蹄涡分支相遇，逐渐形成一个较强的单涡结构，即通道涡。

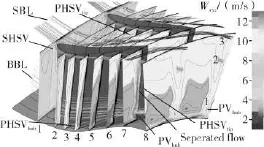
图10 静叶通道内三维空间流线与沿流向截面的速度分布云图

图10显示了详细的二次流发展过程。其中，HSV表示顶部马蹄涡，tip表示叶顶。SHSV和PHSV分别为马蹄涡在吸力面和压力面侧的两个分支。与前述的经典二次流模型不同的是PHSVtip发生从叶顶到叶根的径向运动，而非与吸力面侧的SHSVtip融合。正是叶顶马蹄涡压力面分支的径向运动对吸力面的来流边界层（以BBL标示的流线）产生扰动，导致层流分离。SBL标示的流线表示在叶顶端盖发展的边界层这部分流体沿着端盖在沿流向运动的同时在横向压力梯度的作用下向相邻叶片的吸力面运动，在到达吸力面之前流出了叶片通道，形成了低速区3。由于叶顶马蹄涡的径向运动使得叶根通道涡的强度增强，而叶顶通道涡强度减弱。叶顶通道涡没有形成一个集中的涡核，而是沿径向拉伸至叶中附近。分离流区主要位于低速区1和2之间。由于分离流区非常薄，引起的尾迹较弱，因此层流分离对动叶通道内的影响较小。

4 结论

本文重点研究了低速轴流涡轮在低雷诺数进口条件下，叶片通道内的层流分离流动与二次流动。结论如下：

1）低雷诺数进口条件下，静叶吸力面的分离流发生在转捩之前。求解层流方程可以准确捕捉层流分离的位置。层流分离流有很大的径向运动，且没有再附于叶片表面。

2）AGS模型不能很好模拟分离转捩。DES模拟对层流分离和二次流动模拟结果表现出一定优势。但本文采用的DES模拟网格数量不多，对DES模拟结果可能造成一定影响。今后将进一步针对DES模拟展开网格密度对模拟结果的影响研究。

3）综合比较计算结果可得出DES模拟可以很好地求得低速轴流涡轮内的流动结构，在模拟其他进口条件为低雷诺数的低速轴流涡轮时应优先考虑DES模拟，如果计算资源较匮乏时则可考虑求解层流方程。

4）顶部马蹄涡在吸力面分支的径向运动是引起边界层分离的扰动源。分离流的径向运动导致分离区很薄，分离流没有再附于叶片表面，而是卷入叶片根部的通道涡。

[1]孙爽,雷志军,朱俊强，等.粗糙度对超高负荷低压涡轮边界层影响[J].推进技术,2014,35(3):356-364.

[2]Bons JP,Sondergaard R,Rivir RB..The Fluid Dynamics of LPT Blade Separation Control Using Pulsed Jets[J].ASME Journal of Turbomachinery，2001,124(1)：77-85.

[3]Van Treuren K.W.,Simon T,von Koller M,etal.Measurements in a Turbine Cascade Flow Under Ultra Low Reynolds Number Conditions[J].ASME Journal of Turbomachinery，2002,124(1)：100-106.

[4]Bernardini C.,Benton S.I.,Bons J.P..The Effect of Acoustic Excitation on Boundary Layer Separation of a Highly Loaded LPT Blade[J].ASME Journal of Turbomachinery，2013,135(5): 051001-9.

[5]Matsunuma T.Unsteady Flow Field of an Axial-flow Turbine Rotor ata Low Reynolds Number[J].ASME Journalof Turbomachinery,2007,129(2):360-371.

[6]梁丽萍.低速轴流涡轮内部流动的CFD模拟[M].北京：华北电力大学，2015.

[7]M.T.Schobeiri,B.Öztürk,David E.Ashpis.Effectof Reynolds Number and Periodic Unsteady Wake Flow Condition on Boundary Layer Development,Separation,and Intermittency Behavior Along the Suction Surface of a Low Pressure Turbine Blade[J].ASME Journal of Turbomachinery,2007,129(1): 92-107.

[8]Ali Mahallati，Steen A.Sjolander.Aerodynamics of a Low-pressure Turbine Airfoil at Low Reynolds Numbers-partⅡ:Blade-wake Interaction[J].ASME Journal of Turbomachinery,2012,135(1):011011-10.

[9]Maclsaac G D,Sjolander S A,Praisner T J.Measurements of Losses and Reynolds Stresses in the Secondary Flow Downstream of a Low-speed Linear Turbine Cascade[J].ASME Journalof turbomachinery,2012,134(6):061015-12.

[10]Reinaldo A.Gomes,Stephan Stotz,Franz Blaim,etal.Hot-film Measurements on a Low Pressure Turbine Linear Cascade with Bypass Transition[J].ASME Journal of Turbomachinery,2015, 137(9):091007-11.

[11]宁方飞,徐力平.Spalart-Allmaras湍流模型在内流流场数值模拟中的应用[J].工程热物理学报,2001,22(5):304-306

[12]王晓东,康顺.低速轴流涡轮非定常数值模拟的非线性谐波法[J].工程热物理学报,2009,30(6):949-952.

[13]Merkle C.L.,Sullivan J.Y.,Buelow P.E.O.,etal.Computation of flow with arbitrary equations of state[J].AIAA J.,1998,36(4): 515521.

[14]Abu-Ghannam,B.J.and Shaw,R.,Natural Transition of Boundary Layer the Effect of Turbulent Pressure Gradient and Flow History[J].Journal of Mechanical Engineering Science, 1980,22(5):213-228.

[15]Wang X.D..CFD Simulation of Complex Flows in Turbomachinery and Robust Optimization of Blade Design[D].Belgium: Vrije UniversiteitBrussel,2010.

■

在低雷诺数进口条件下，低速涡轮叶片绕流可能存在大范围的层流流动、层流分离流动、边界层转捩和显著的径向二次流动，流动结构复杂，给精确的数值模拟提出挑战。本文对AIST低速轴流单级涡轮内部流动进行数值模拟，其中静叶通道分别采用全层流模型、全湍流模型、Abu-Ghannam＆amp;Shaw (AGS)转捩模型和分离涡模拟(DES)方法，动叶通道求解RANS方程，湍流模型为Spalrat-Allmaras一方程模型。与实验结果对比显示，层流模型准确地捕捉到了静叶叶片吸力面层流分离的分离位置。三维流动结构分析显示，在很低的雷诺数条件下，静叶吸力面层流分离流产生很大的径向运动，没有再附于叶片表面，被卷入叶片根部的通道涡中。

轴流涡轮；低速；数值模拟；层流分离；二次流

Comparisons of Numerical Simulation Methods of Lam inar Flow Separation on Blade Surface W ithin a Low Speed AxialTurbine

Wang Xiao-dong,Liu Xiao-jie,Liang Li-ping,Kang Shun/School of Energy Power and Mechanical Engineering,North China Electric Power University

Abstract：Under inlet conditions with a low Reynolds number,laminar flow, laminar flow separation,transition flow and radial secondary flow may exist in large range on the blade surface of a low speed turbine.The complex flow structuremakes accurate numerical simulations a challenges.Numerical simulations are performed on internal flows within the low speed single stage axial turbine of AIST.Different models,such as fully laminar flow model, fully turbulent flow model,Abu-Ghannam ＆amp;Shaw(AGS)transition model,and detached eddy simulation(DES)are used respectively within the stator blade passage.The RANSequations are solved in the rotor blade passage.One equation turbulence model,the Spalart-Allmaras model,is employed for turbulence modeling.According to the validation with experimental result,the laminar simulation accurately captures the position of laminar separation on the stator blade's suction surface.The three-dimensional flow structure analysis reveals that the laminar separated flow has large spanwise movement, which is wrapped into the hub passage vortex rather than reattaching the blade surface.

axial turbine；low speed；numerical simulation laminar separation；secondary flow

TH133;TK05

A

1006-8155（2016）03-0025-06

10.16492/j.fjjs.2016.03.0073

国家自然科学基金（51206052）；中央在京高校重大成果转化项目（ZDZH20141005401）；中央高校基本科研业务费专项资金资助（2014ZZD04）

2015-09-18北京102206