二分法快速求解Duffing混沌阈值的微弱信号检测
2016-12-20叶家敏
张 菁, 王 斌, 叶家敏
(1. 上海工程技术大学 电子电气工程学院,上海 201620;2. 上海西南工程学校,上海 201100)
·计算机技术应用·
二分法快速求解Duffing混沌阈值的微弱信号检测
张 菁1, 王 斌2, 叶家敏2
(1. 上海工程技术大学 电子电气工程学院,上海 201620;2. 上海西南工程学校,上海 201100)

针对改进型Duffing混沌系统检测微弱信号,求解Lyapunov阈值时间过长问题,提出二分法实现快速求解Duffing系统由混沌到周期态的阈值。首先, 以0.1步长的Lyapunov指数确定一个粗略的阈值;然后根据对分法快速收索Duffing-Holmes振子混沌阈值的精确值,这一算法大大提高了阈值搜索速度,通过识别微弱信号仿真事例证明这种方法的有效性。
二分法; Duffing; 微弱信号; Lyapunov指数
0 引 言
微弱信号检测技术是采用电子学、信息论、计算机及物理学的方法,分析噪声产生的原因和规律,研究被测信号的特点与相关性,检测被噪声淹没的微弱有用信号。传统的建立在FFT的信号处理无法在强噪声中识别或提取微弱的奇异信号[1],考虑到改进型Duffing混沌系统对外界干扰的极端敏感性,可用于微弱信号的检测[2]。该方法的目的是找到Duffing(LY)系统从混沌态到周期态变化的阈值,同时能够获得Duffing(LY)系统状态会随内置摄动力r的从小变大出现有规律的变化,因此搜索阈值微弱信号混沌检测中的一个重要内容。应用前需确定该系统是混沌的,这就涉及到混沌判别[3]。本文给出了基于改进型Duffing混沌系统,利用Lyapunov特性指数判别法并结合二分法快速求解Duffing系统阈值从而检测出微弱信号的方法。
1 Duffing混沌系统的改进型—Duffing(LY)
原Duffing系统方程为:
x″(t)+kx′(t)-ax(t)+bx3(t)=r cos ωt
(1)
由于原Duffing系统对不同的信号敏感程度不同,建立对信号敏感的混沌系统是信号检测的首要条件。为了更好地检测微弱信号,应对Duffing系统方程进行改进。从微弱信号的检测能力的下限,混沌系统检测信噪比,以及系统混沌判定的几方面综合考虑[4-5],得到改进型Duffing系统为:
x″(t)+kx′(t)-bx3(t)+cx5(t)=r cos ωt
(2)
其中:k为阻尼系数;-bx3(t)+cx5(t)为改进后的非线性恢复力;rcosωt为系统摄动力。式(2)称为改进型Duffing(LY)并对状态的变化非常敏感,可通过判别系统处于混沌态还是周期态,检测信号中是否含有微弱奇异信号[6]。
2 Lyapunov指数定量判别方法
判别系统混沌态和周期态的临界点就是找到系统的阈值,如果无法找到阈值,表示系统不存在混沌[7]。Lyapunov特性指数是一个经典的混沌判别方法,是对混沌系统敏感性的度量,它表征了系统在相平面中运动轨道的收敛或发散的平均指数率[8],其定义由文献[9]给出。
将方程(2)作如下变换:
(3)
当系统呈现大尺度周期状态时,2个Lyapunov指数(LE)均是负值;当系统为混沌状态时,至少有1个Lyapunov指数是正值。
设初始条件为x(0)=1,x′(0)=1, 在r=[0.5, 1]选择30个点值分别计算LE,r的计算精度是小数点2位。图1是LE的曲线图,在r=0.70, 系统呈现混沌状态;r=0.78, 系统呈现周期态,见图2和图3。
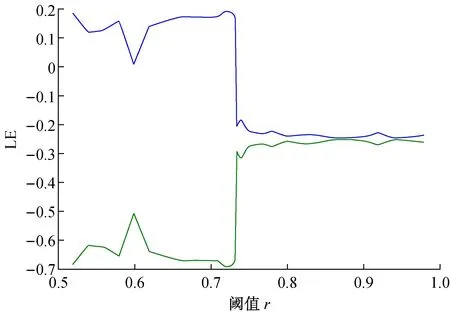
图1 Lyapunov指数与r的关系

图2 r=0.70时系统时域响应、相平面和LE
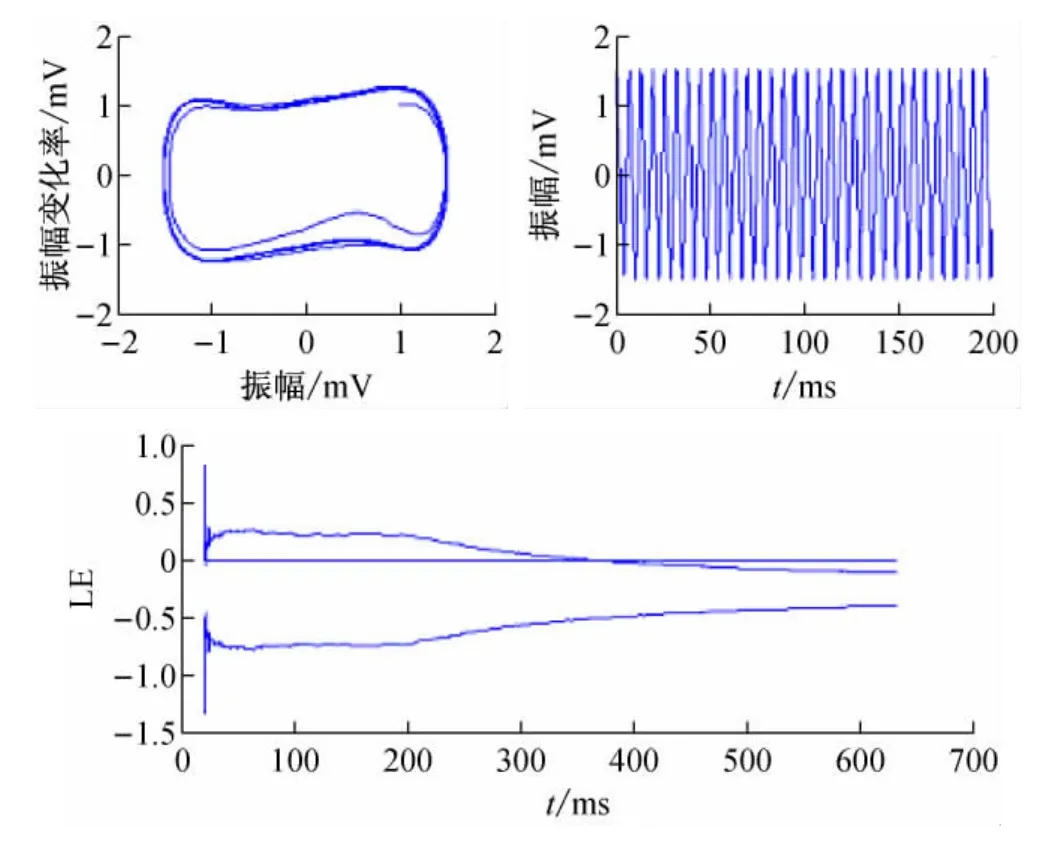
图3 r=0.78时系统时域响应、相平面和LE
3 二分法与直观法确定系统精确域值
由于二分法适用于快速求取最优解[10],可将其用于对阈值进行精确定位。首先粗略计算Lyapunov指数(初始条件为x(0)=1,x′(0)=1,有效位为1),得到系统的阈值大致范围为r=[0.7,0.8]。随后,在该区间内用二分法快速求取精确阈值(精度为6),步骤如下:
(1) 由于0.7对应系统混沌态,而0.8对应周期态,取 0.7~0.8的中间值r=0.75。
(2) 由于r=0.75对应周期态,所以取r的区间为[0.7,0.75]。然后r从0.7~0.75以步长为0.01 增加到0.71,该值对应混沌态,0.72对应周期态,取0.71 ~ 0.72的中间值r=0.715。
(3) 由于0.715对应的是混沌态,此时r的取值范围是[0.715,0.72]。然后r从0.715~0.72以步长为0.001增加到0.718,r=0.717对应周期态,而0.718对应混沌态,取0.717~0.718的中间值0.717 5。
(4) 由于0.717 5对应的是混沌态,所以r的取值范围是[0.717,0.717 5]。然后r从0.717~0.717 5以步长为0.000 1增加到0.717 3,r=0.717 3对应混沌态,而0.717 4对应周期态,取0.717 3~0.717 4的中间值0.717 35。
(5) 由于0.717 35对应的是周期态,则r的取值范围是[0.717 3,0.717 35]。然后r从0.717 3~0.717 35以步长为0.000 01增加到0.717 32,r=0.717 32对应混沌态,而0.717 33对应周期态,0.7173 2~0.717 33的中间值是0.717 325。
(6) 由于r=0.717 325对应的是周期态,所以r的取值范围是[0.717 325,0.717 33]。 然后r从0.717 325到0.717 33以步长为0.000 001增加到0.717 329,r=0.717 329这个值对应混沌态,而0.717 33对应周期态。
(7) 最后的阈值确定为0.717 329。当弱周期信号嵌入到系统(3)时,这个系统呈现大尺度周期态。这个计算过程见表1。

表1 二分法求系统阈值
从计算过程看出,确定一个6位阈值最多搜索运行30次,阈的求解速度得到很大改进。
4 结 语
提出了利用改进型Duffing混沌系统检测微弱信号的方法。具体过成为:先将要检测的信号做为扰动输入到Duffing(YL)系统作为外部摄动力;再通过确定合理的阈值识别检测信号中是否含有微弱的奇异信号。而阈值的确定需要将二分法与Lyapunov指数算法相结合运用。首先通过Lyapunov指数判别法确定阈值的范围;随后在该范围内用二分法快速求出阈值。这种算法能够快速得从混沌到周期的系统临界阈值,确定Duffing(YL)系统的阈值,降低系统Lyapunov指数的计算时间。
[1] 高振斌,张 晨,李景春. 混沌算法和子空间算法应用在微弱信号检测中的比较[J]. 科学技术与工程,2014,14(1): 235-239.
[2] 夏均忠,刘远宏,冷永刚,等.微弱信号检测方法的现状分析[J].噪声与振动,2011, 31(3): 156-161.
[3] 孙玉胜,詹小霞,石 军,等.基于Duffing振子的微弱信号检测[J].郑州轻工业学院学报,2012,27(5):81-84.
[4] Dr Ivana Kovacic, Michael J. Brennan.The Duffing Equation: Nonlinear Oscillators and their Behaviour[M].New York City:John Wiley & Sons,2011:82-84.
[5] 樊养余,李利品,党瑞荣,等.基于随机共振的任意大频率微弱信号检测方法研究[J].仪器仪表学报,2013,34(3):566-572.
[6] 程凤芹,曲 娜,赵 璐,等.基于特定混沌系统的微弱信号检测仿真研究[J].计测技术,2011,31(5):1-2.
[7] Patel V.N. Tandon N., Pandey R.K.. Defect detection in deep groove ball bearing in presence of external vibration using envelope analysis and Duffing oscillator[J].Measurement,2012,45(5):960-970.
[8] Ch. Skokos. Dynamics of Small Solar System Bodies and Exoplanets[C ].New York City: Spinger,2010:63-135.
[9] Lai-Sang Young. Mathematical theory of Lyapunov exponents[J].Mathematical and Theoretical, 2013,46(25):1916-1930.
[10] Bachrathy, Dániel, and Gábor Stépán. Bisection method in higher dimensions and the efficiency number[J].Mechanical Engineering,2012,56 (2): 81-86.
[11] Damodarasamy S., Raman S.. Inexpensive system for classifying tool wear states using pattern recognition[J]. Wear,1993, 170(2):149-160.
[12] Wanqing song, and ZHANG Jing: Tool State Detection by Harmonic Wavelet and Sample Entropy [J]. Chinese Journal of Mechanical Engineering, 2011, 24(6):1068-1073.
[13] Yao Y X, Li X, Yuan Z J. Tool wear detection with fuzzy classification and wavelet fuzzy neural network[J]. International Journal: Machine Tool & Manufacture 1999,39(10): 1525-1538.
[14] Cho S. S., Komvopoulos K. Correlation Between Acoustic Emission and Wear of Multi-Layer Ceramic Coated Carbide Tools[J]. Transactions of the ASME,1997,119(2):238-246.
[15] Ding Liu, Haipeng Ren, Li Song. Weak Signal Detection Based On Chaotic Oscillator[C]. Xian (China): Industry Applications Conference, Fourtieth IAS Annual Meeting, 2005, 3: 2054-2058.
[16] Julien Clinton Sprott.. Chaos and Time-Series Analysis[M]. University Press, Oxford, UK & New York, USA, 2003.
[17] Florian Grond, Hans H. Diebner. Local Lyapunov exponents for dissipative continuous systems[J]. Chaos, Solitons and Fractals,2005, 23(5): 1809-1817.
[18] 聂春燕,石要武. 基于互相关检测和混沌理论的弱信号检测方法研究[J]. 仪 器仪表学报, 2001,22(1):33-35.
[19] 刘立,孙军. 基于混沌振子的微弱信号检测方法研究[J]. 沈阳农业大学学报,2005, 36(6):667-67.
[20] Udwadia F E, von Bremen H F. Computation of Lyapunov characteristic exponents for continuous dynamic system[J]. Zeitschrift für Angewandte Mathematik und Physik (ZAMP), 2001, 53(1):123-146.
Quickly Solving the Threshold of Duffing Chaos System for Weak Signal Detecting by Bisection Algorithm
ZHANGJing1,WANGBin2,YEJia-min2
(1.School of Electronic & Electrical Engineering, Shanghai University of Science and Engineering,Shanghai 201620, China; 2.Shanghai Southwest Engineering School, Shanghai 201100, China)
In the improved Duffing system, detection signal is quite weak, hence, solving the chaos threshold takes a lot of time when one applies Lyapunov exponent criterion. The paper proposes a bisection algorithm to solve the problem. The algorithm can figure out the threshold value whcih makes Duffing system transfer from chaos state to period state. First, we take 0.1 as the step length to find a threshold roughly based on the Lyapunov exponent. Then the bisection algorithm figures out the exact value for the threshold. The speed of calculating is speeded a lot, Simulation result proves the validity of this method.
bisection algorithm; Duffing; weak signal; Lyapunov exponent
2015-07-09
国家自然科学基金项目(51477099和51477100)
张 菁(1969-),女,上海人,副教授,主要研究方向为电气工程及其自动化、机械电子等。E-mail: 1768283350@qq.com
TN 98
A
1006-7167(2016)02-0086-03
