永磁同步电动机调速系统动态分段控制策略

吴国中,丁 强,2

(1.南京工业职业技术学院,南京 210023; 2.南京航空航天大学,南京 210016)



永磁同步电动机调速系统动态分段控制策略

吴国中1,丁 强1,2

(1.南京工业职业技术学院,南京 210023; 2.南京航空航天大学,南京 210016)

转速动态性能是高性能永磁同步调速系统主要性能指标之一。为提高调速系统转速动态调节的控制精度及响应时间，提出一种算法设计实现简便的动态分段控制策略，该算法建立在详细分析转速动态三段调节的基础上，根据每段的不同特点分别设计不同的控制算法加以控制。最后，通过仿真和实验验证所提控制策略的正确性和有效性。

永磁同步电动机；调速系统；动态性能；分段控制

0 引 言

伴随稀土永磁材料的发明，永磁电机由于在体积、效率、功率密度等方面的优势逐渐被工业界和学术界所关注[1-4]。采用正弦波驱动的永磁电机称为永磁同步电动机(以下简称PMSM),而采用方波驱动的永磁电机称为永磁无刷直流电动机(以下简称PMBLDC)。在高性能调速领域，由于较小的转矩脉动利于调速系统动、静态性能的提升，使得永磁同步电动机应用多于永磁无刷直流电机。

转速稳态精度和动态调节性能是高性能调速系统首要关注的两个方面，通过合理设计转速控制环的控制策略能够实现这两方面性能的兼顾。现有的PMSM转速闭环控制通常是建立在直接转矩控制和矢量控制基础上的，常用的控制策略为PI控制。然而，PI控制由于存在参数局部适应性及动态性能折中的问题，使得诸如自适应控制、滑模变结构控制、自抗扰控制及智能控制等先进控制策略均被引入转速调节中[5-8]，但先进的控制策略不可避免的使得控制算法设计和实现较为复杂。

为克服PI控制动态过程转速响应和超调无法兼顾的不足，同时克服先进控制策略算法设计与实现复杂的问题，本文提出一种算法设计及实现简单的转速动态分段控制策略，并在阐述算法设计原理基础上，进行相关仿真和实验验证。

1 PMSM数学模型与矢量控制

永磁同步电动机在两相旋转坐标系下的数学模型由电压方程、磁链方程、转矩方程和运动方程组成，其中电压方程:

(1)

磁链方程:

(2)

转矩方程:

(3)

运动方程:

(4)

式中：ud，uq，id，iq，ψd，ψq，Ld，Lq分别表示电机d,q轴电压、电流、磁链、电感；ω，J，pn分别表示电角速度、转动惯量和转子极对数；Te，Tl分别表示电磁转矩和负载转矩。

依据上述数学模型，可以对PMSM采取矢量控制策略。在所有矢量控制策略中，id=0控制最为简单且电枢电流全部用于产生转矩、永磁体不存在退磁风险，其原理框图如图1所示。

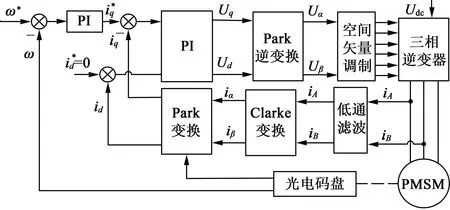
图1 id=0矢量控制原理图

2 转速动态分段控制策略

传统PI控制的PMSM的转速控制策略，存在动态响应时间与超调折中设计的问题，响应时间和超调量无法兼顾，为解决该问题本文提出一种新型转速动态分段控制策略。

2.1 转速动态过程分析

假定给定转速t1时刻突降，电机转速动态调节过程如图2所示。

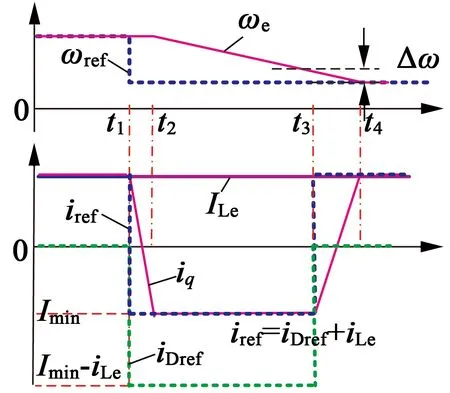
图2 电机转速动态调节过程分析

第一阶段(t1～t2)由于电流环响应的延迟，造成转速响应的滞后，可近似认为转速不变。该阶段时间较短，通常一个控制周期内即可完成。

第二阶段(t2～t3)由于电流环开始响应工作，转速处于为恒减速阶段。该阶段为动态调节时间的主要部分，直接影响转速动态响应时间。若能够缩短此阶段持续时间，有利于提高转速响应速度。

第三阶段(t3～t4)为转速稳定阶段。该阶段实际转速与给定转速较为接近，其调节效果影响转速超调量。

2.2 电流给定算法设计

在转速突变的过程中，电流给定值iref由动态分量iDref和稳态分量iLe两部分组成。动态分量作用时间由转速调节过程决定，稳态分量由电机负载决定。

(5)

假定转速调节过程，负载转矩保持不变，根据上节动态调节过程分析可知，缩短第二阶段(t2～t3)调节时间能够减小动态调节过程且不会影响转速响应超调，因此，第二阶段电流给定值iref2可设置较大。此外，由于第一阶段(t1～t2)第一阶段调节时间非常短，在此区间内的电流给定值iref1设置为等于iref2。

(6)

式中：Im为保证电机及功率变换装置正常工作下可输出最大电流。

第三阶段(t3～t4)影响转速超调量，需要进一步细化分段控制，其给定电流iref3可采取如下分段函数实现。

(7)

式中：ωerr为给定转速与实际转速的差值；m为控制切换阈值。

2.3 降阶负载转矩观测器

由上节电流算法设计过程可以看出，转速调节三个阶段动态电流分量给定值都与稳态分量iLe相关。然而，上述过程是假定负载转矩不变的前提下进行，在电机实际运行中该假设不一定任意时刻都能得到满足。因此，为消除负载转矩变化对控制性能的影响，本文根据电机数学模型设计降阶负载转矩观测器以补偿转矩变化的影响。

根据PMSM的数学模型，可以设计降阶观测器状态方程:

(8)

为适应数字控制，上式经过离散化可得:

(9)

式中：H=[h1h2]T为观测器控制参数。

由式(9)可以得到降阶转矩观测器原理图，如图3所示。

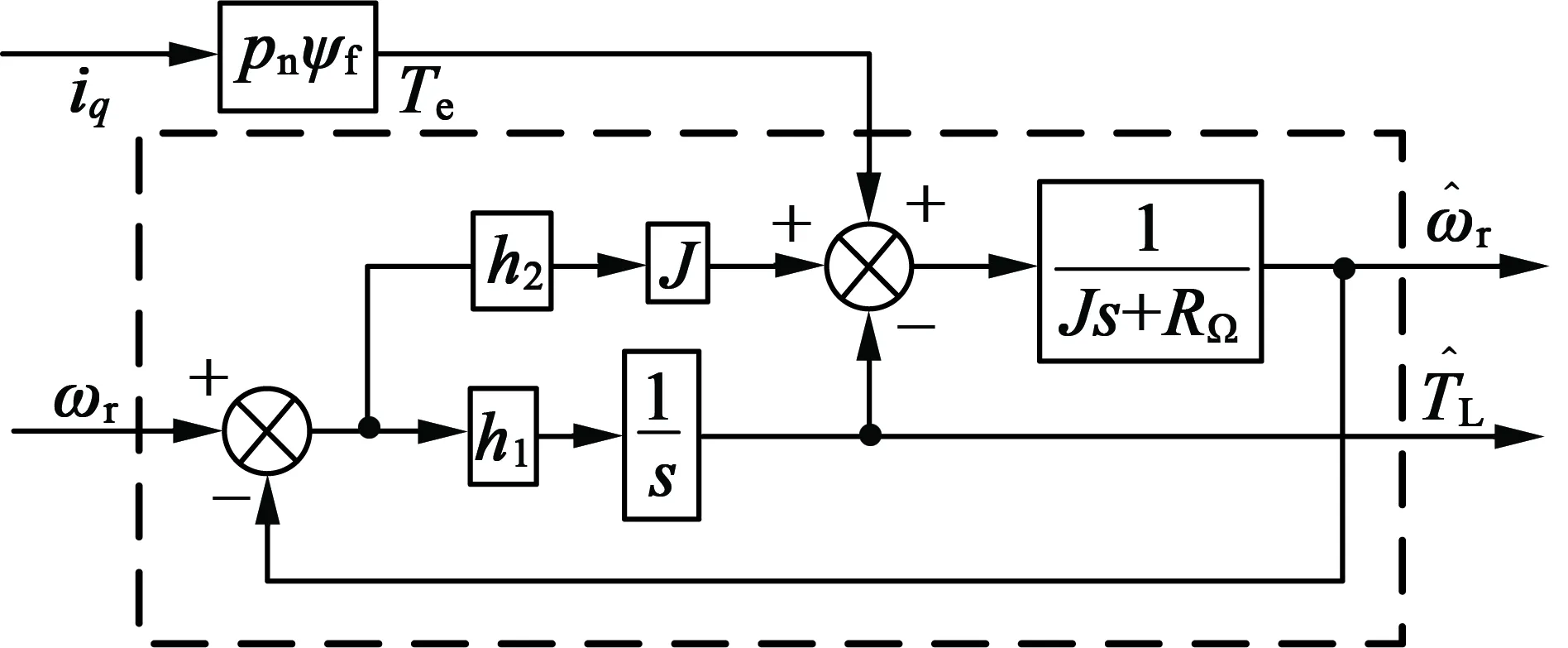
图3 转矩降阶观测器原理框图

3 实验结果及分析

为验证本文所提分段控制策略的有效性和正确性，在一台永磁同步电动机上进行相关的仿真和实验验证。仿真电机的参数如表1所示。

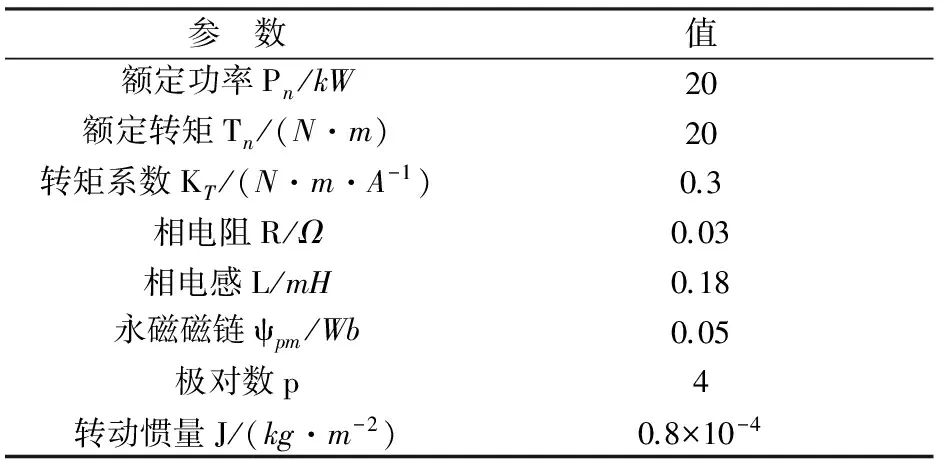
表1 电机主要参数

图4为转矩观测器的仿真波形。仿真过程中电机给定转速为6 000r/min(即628rad/s)，在0.06s时电机转矩从满载(20N·m)突变为半载状态(10N·m)。可以看出，从转矩观测器得到的计算转矩和计算转速能够较好跟踪实际转矩和实际转速且不存在稳态误差。此外，转矩观测器的动态响应较好，动态调节过程在10ms内能够完成。

(a) 转速观测效果

(b) 转矩观测效果

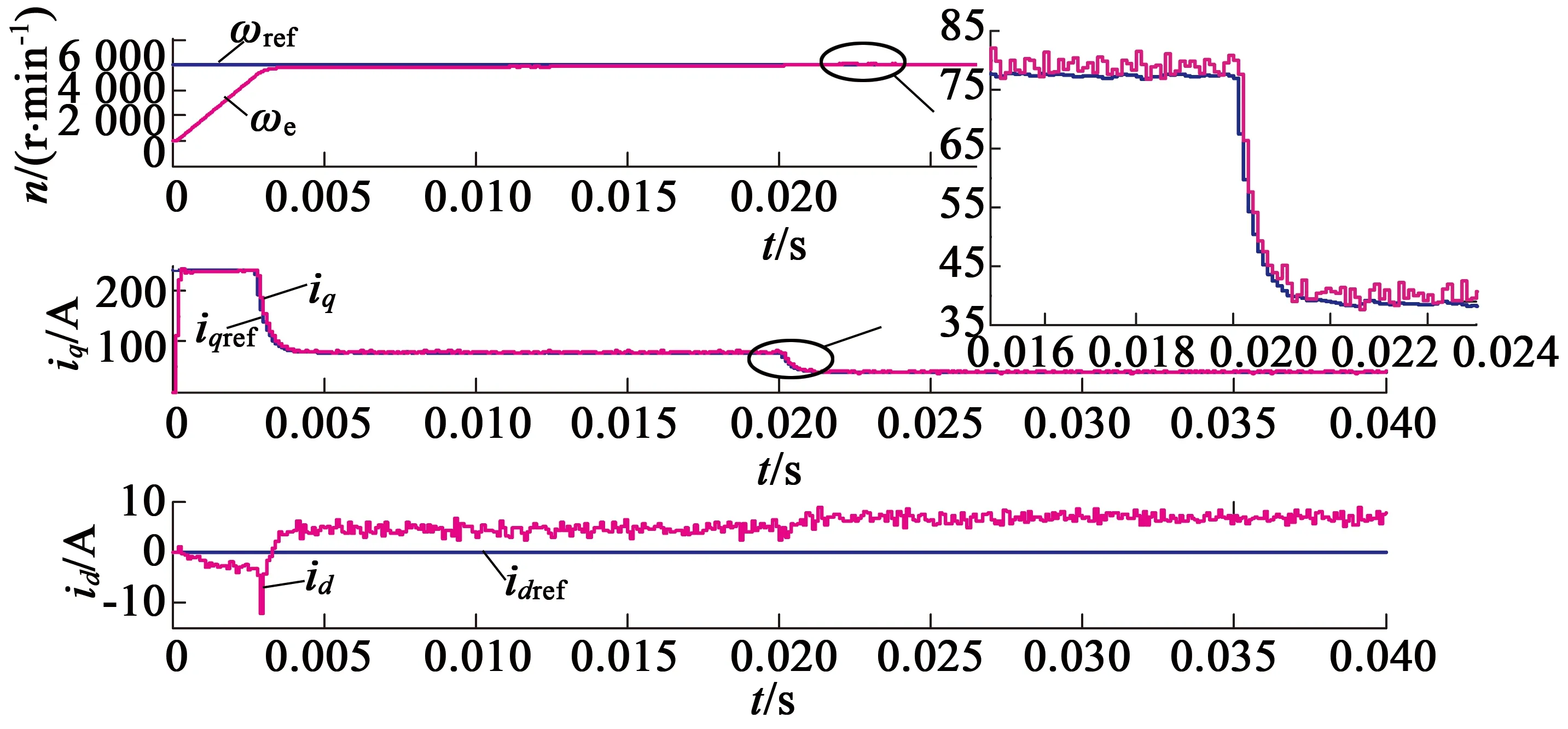
为验证本文所提分段控制策略的有效性，对电机转速和转矩突降分别采用传统PI控制和分段控制。仿真过程中，在0.02s时电机转速由6 000r/min突变为3 000r/min；负载转矩由20N·m变为10N·m；PI控制器限幅值和分段控制策略的Im设为相同，以保证公平对比。图5和图6为其相关仿真波形。对比图5和图6可以看出，采用PI控制转速响应存在超调且动态调节时间为2.5ms，负载转矩突变时PI控制下电流环响应时间为3ms，而采用分段控制时转速响应无超调且响应时间为1ms且负载突变时电流环响应时间为0.5ms。因此，无论转速响应还是超调量分段控制策略均优于PI控制。

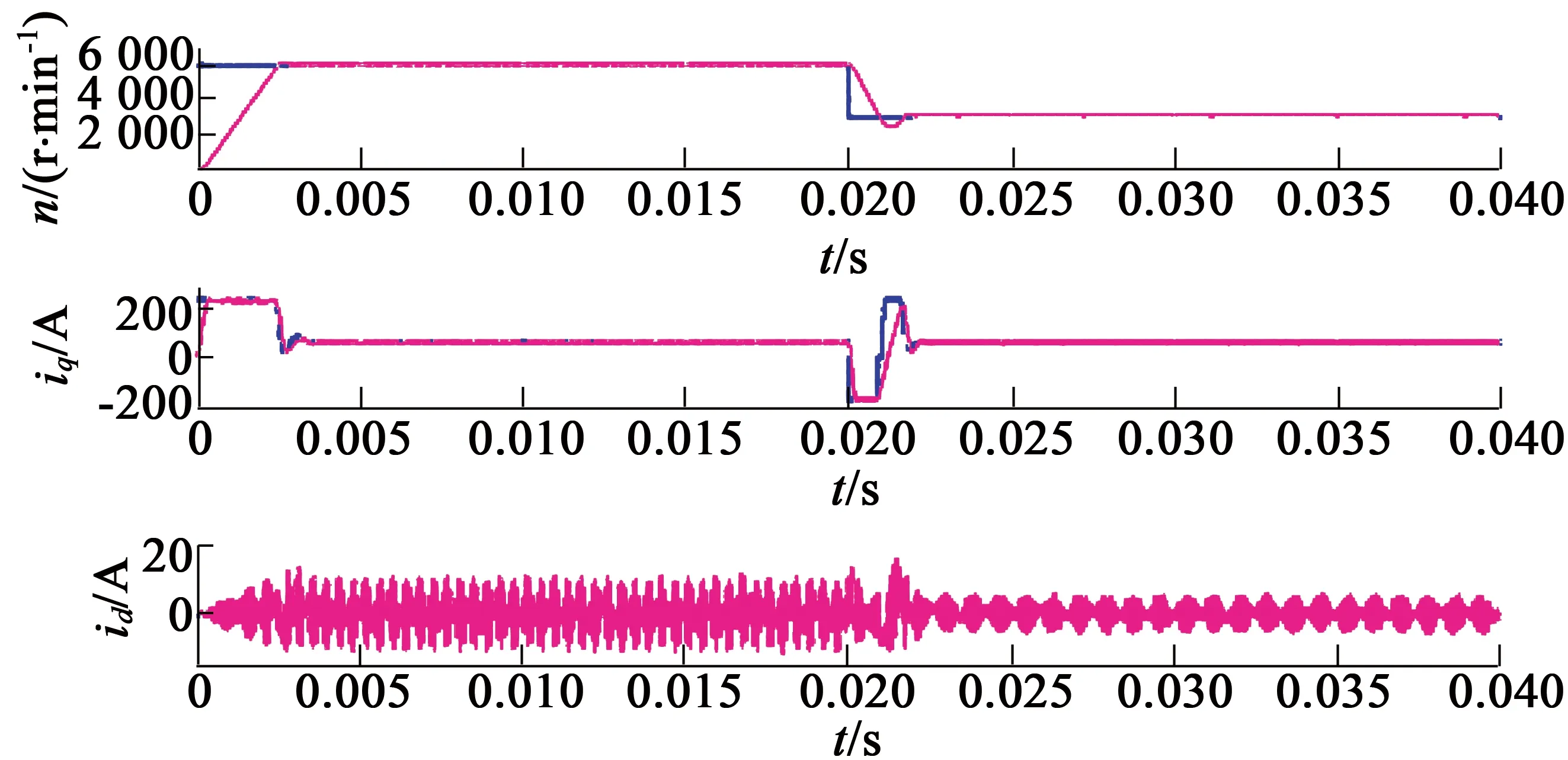
(a) 转速突变

(b) 转矩突变

(a) 转速突变

(b) 转矩突变

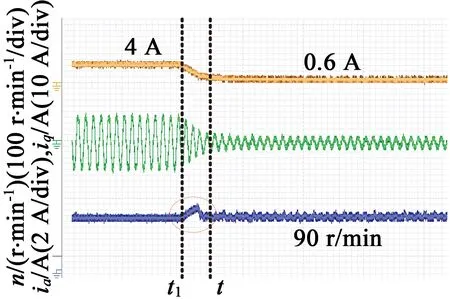
为验证分段控制策略的有效性，在一台永磁同步电动机上进行实验验证，主控制芯片采用TIDSP28335。实验过程中，同样对比PI控制与分段控制策略的控制效果，实验波形如图7和图8所示。在t1时刻电机给定转速从200r/min突变为450r/min。可以看出，转速响应无超调且动态调节时间为

(a) 转速响应波形

(b) 突降负载波形

(a) 转速响应波形

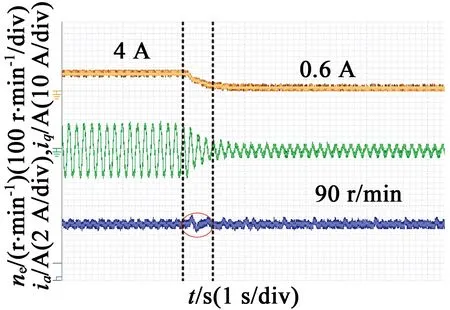
(b) 突降负载波形

140ms，要优于PI控制下240ms的响应时间。此外，当负载由4N·m突降时，分段控制策略的动态过程最大转速波动为8r/min，而PI控制下最大转速波动为35r/min。

4 结 语

本文为提高永磁同步电动机调速系统的动态性能提出一种转速动态分段控制策略，在阐述该算法基本控制原理后，给出具体设计流程。在此基础上为验证所提算法的有效性同时进行仿真和实验验证。仿真和实验结果表明该算法可以有效减小转速调节响应时间和动态调节过程转速波。

[1] 张涵,谢宝昌.永磁同步电动机转子优化设计与研究[J].微特电机,2015,43(1):25-27.

[2] 张永平,段小丽,郭英桂.内置式永磁同步电动机转子加装工艺设计[J].微特电机,2015,43(11):83-85.

[3] 田兵,安群涛.基于磁饱和效应的表贴式永磁同步电动机初始位置检测方法[J].电工技术学报,2016,31(1):155-164.

[4] 郝雯娟,邓智泉.一种定子齿错位的模块化直线永磁磁通切换电机[J].微特电机,2015,43(11): 14-18.

[5]LIShihua,ZONGKai,LIUHuixian.Acompositespeedcontrollerbasedonasecond-ordermodelofpermanentmagnetsynchronousmotorsystem[J].TransactionsoftheInstituteMeasurControl,2011,33(5):522-541.

[6]EKERI,AKINALSA.Slidingmodecontrolwithintegralactionandexperimentalapplicationtoanelectromechanicalsystem[C]//ComputationalIntelligenceMethodsandApplications.2005.

[7] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.

[8] 曹先庆,朱建光,唐任远.基于模糊神经网络的永磁同步电动机矢量控制系统[J].中国电机工程学报，2006,26(1):137-141.

Dynamic Subsection Control Strategy for PMSM Speed Regulation Systems

WU Guo-zhong1, DING Qiang1, 2

(1.Nanjing Institute of Industry Technology,Nanjing 210023,China;2. Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

Dynamic performance of speed regulation is one of important performance index for high performance permanent magnet synchronous machine drive systems. To improve control accuracy and response time of speed control, a simple dynamic subsection control strategy was proposed in this paper. On the basis of detailed analysis about three stages of dynamic regulation, different control algorithms were imposed on different stages. Finally, relevant simulations and experiments were performed to verify the correctness of proposed strategy.

PMSM; speed regulation system; dynamic performance; subsection control

2016-05-03

江苏省品牌专业建设工程项目(PPZY2015B189);第三批高校中青年优秀教师出国研修项目(苏教师[2013]8)

TM351;TM341

A

1004-7018(2016)10-0061-03

吴国中(1974-)，男，副教授，硕士研究生，研究方向为电机控制。