兆瓦级风电制动器热-结构耦合仿真研究
2016-12-20沙智华刘楠刘宇马付建尹剑张生芳
沙智华,刘楠,刘宇,马付建,尹剑,张生芳
(大连交通大学 机械工程学院,辽宁 大连 116028) *
兆瓦级风电制动器热-结构耦合仿真研究
沙智华,刘楠,刘宇,马付建,尹剑,张生芳
(大连交通大学 机械工程学院,辽宁 大连 116028)*
针对大兆瓦风电制动器制动过程,考虑制动摩擦副作用区域宽度及其影响下的线速度径向差异,提出速度梯度循环法,对制动过程摩擦副进行热-结构耦合分析.基于ANSYS软件建立制动器摩擦副三维瞬态传热有限元模型,运用速度梯度循环法推导出热流密度的加载式,用以计算制动过程中产生的摩擦热流,对制动区域温度场进行数值模拟.从分析结果表明制动闸片摩擦区域温度分布在制动盘径向呈现弧度明显的等温分布,温度梯度随半径增大而增大.以速度梯度循环法将热分析结果代入结构场对闸片摩擦区域受力及变形进行耦合分析并预估其磨损状况.通过与传统均匀加载方法对比发现使用速度梯度循环法的分析结果与实际更为接近.所提出的分析方法为模拟大尺寸盘式制动器的摩擦制动过程提供参考.
风电制动器; 热-结构耦合; 速度梯度循环法 ;有限元仿真
0 引言
风力发电机组在超风速、需要故障排除及日常维护等情况时需要停机制动,为保证在最短时间内停机和在风机维护时的操作安全,需要风电制动器提供机械制动,因此风电制动器是风力发电必不可少的配套装置.在制动器工作时,利用非旋转元件与旋转元件之间的相互摩擦来阻止转动或转动的趋势,最终实现风机系统的停机.在这个过程中制动摩擦时,由于摩擦副接触不均匀,实际接触面积远小于名义接触面积且接触不连续造成接触表面温度分布不均匀,导致盘片发生热变形,直接影响接触状态和接触压力,从而影响摩擦热流输入强度,这种耦合行为导致摩擦材料热弹性不稳定(Thermoelastic Instability, TEI)[1],使得风电制动器产生振动与噪声[2].同时,热应力的作用易使摩擦材料热衰退,产生初始裂纹并加剧摩擦副表面刮削现象[3].由此可见,在制动过程中,温度场、应力场对风电制动器的制动效能有很大影响,二者的耦合分析是制动器设计的重要内容和摩擦副材料选择的重要理论依据.
制动摩擦表面温度模型早期由Bolk[4]提出,后来Jaeger对该理论进行了发展,论证并提出了在半无限体表面矩形移动热源的数学模型[5],此后的研究工作大多集中在多热源以及热源之间的相互作用对摩擦表面温度的影响.华林[6]等人基于盘式制动器制动过程中能量耗散的研究,建立了紧急制动过程中制动盘与摩擦片瞬态温度场分析的有限元模型.王新波[7]等人,运用循环迭代的计算方法加载热流密度.该方法可以较好的模拟制动盘周向的应力应变分布,但其并未考虑制动盘各节点径向旋转线速度差异对实际制动过程的影响.
本文根据某型号大兆瓦风电制动器的实际制动工况,并考虑了温度场、结构场在制动闸片上的耦合问题.采用ANSYS软件建立制动过程的三维瞬态热-结构耦合模型.重点研究制动区域摩擦热流的加载方式,提出速度梯度循环加载的方法,并将在笛卡尔坐标系下的传统耦合模型用柱坐标表达,简化了热载荷的加载.解释了TEI现象对制动闸片应力及应变分布的影响并预估其磨损状况.最后通过与传统均匀加载方法对比论证速度梯度循环法分析的可靠性.
1 制动器热-结构耦合模型的建立
1.1 热传导模型的建立
盘式制动器在进行制动工作时,将生成大量摩擦热,并使制动盘、闸片的温度呈现梯度分布.盘式制动器的主要传热方式为热传导和热对流,由于制动过程中温度较高,也会产生少量热辐射.因此在建立热传导模型时,本文做以下假设:
(1) 制动的过程中摩擦系数μ不变;
(2) 制动时,制动盘、闸片的接触面上各个点的瞬时温度对应相等,热流密度根据盘与闸片的材料属性自然分配;
(3) 制动盘、闸片的接触界面为理想平面;
(4) 制动过程中的摩擦功全部转化为摩擦热.因此在计算时,可将制动盘、制动闸片的热流输入作为边界热流输入,则摩擦表面输入热流密度满足.
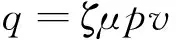
(1)
为简化后续热流密度加载算法,选择柱坐标系,可将式(1)改写为
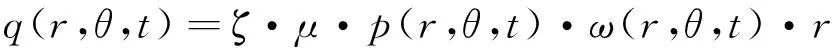
(2)
其中,q(r,θ,t)为t时刻制动盘柱坐标下(r,θ)处吸收的热流密度,ζ为摩擦热分配比例,μ为摩擦系数,p(r,θ,t)为摩擦副的面压力,ω(r,θ,t)为制动盘角速度.
(5)制动盘与制动闸片的材料为各向同性材料,在制动过程中材料的热物性参数不随温度变化而改变.
在制动过程中,制动盘与制动闸片之间存在自然热传导和摩擦热流密度输入[8].根据假设(3)制动闸片的温度与制动盘的温度相等,即自然热传导和摩擦热流密度输入关系为:
(3)
其中,λp为制动闸片热导率,Tp为制动闸片的温度.
1.2 热应力的计算
假设材料在制动过程中只发生线弹性变形.物体由于热膨胀只产生线应变,剪切应变为零.
这种由于材料热变形产生的应变可以看作是物体的初应变.在计算应力时包含初应变项,代入热流密度可以得出热应力的关系式为
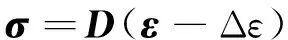
(4)
其中,σ为材料应力矩阵,D为材料弹性矩阵,ε为材料应变矩阵,Δε为温度变化引起的温度应变.
对于三维模型,综合制动闸片温度表达式[9]得出:
(5)
其中,α为材料应力矩阵,Tp为制动闸片的温度,T0为初始温度.
1.3 边界条件
根据制动器实际工况,可以认为制动闸片不动,制动盘做逆时针转动.由于制动压力作用在制动闸片摩擦面背面,假设作用在此作用面上的压力是均布的,但考虑制动盘、制动闸片的弹性变形.制动闸片是固接在制动连杆上并将闸片两侧凹槽安装在导轨上可沿导轨上下滑动,故对制动闸片施加X,Z轴两个方向的固定约束,如图1所示.
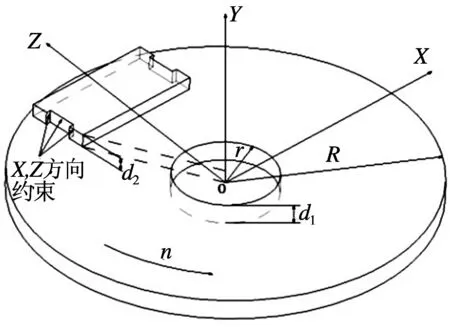
图1 制动摩擦副相对位置关系及位移约束示意图
2 热流密度速度梯度循环加载方法
热流密度的加载是温度场模拟的关键,温度场的准确模拟也是热应力的计算以及后续得出有效热结构耦合分析结果的基础.
为了给制动区域的每一摩擦作用单元准确分配实际工况下的热流密度,在加载式的推导过程中采用归一化思想用以确定比例系数.
2.1 热流密度加载式的理论推导
由式(2)可知,热流密度是关于摩擦热分配比例、摩擦系数、摩擦副的面压力、角速度以及径向半径的函数,由假设(1)、(3)可知:摩擦系数μ不变,制动闸片受均布压力,故摩擦副的面压力p不变,因此热流密度与制动盘的转速和半径r有关.且热流密度与柱坐标半径(制动盘旋转轴距制动区域的每一摩擦作用单元的距离)成正比,即
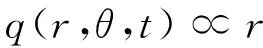
(6)
设比例系数为k1,因此公式可改写为
(7)
在制动过程中整个制动区域每一时刻的总热流密度
(8)
其中,n为此有限元模型中制动区域在该时刻的有效摩擦面积上的单元数;qi为制动区域任意摩擦作用单元的热流密度.
将式(8)适当变形从而求得比例系数
(9)
将式(9)代入式(8)最终得到每一摩擦作用单元的热流密度
(10)
2.2 摩擦功加载式理论推导
基于假设(4)摩擦热全部由摩擦力做功产生,所以本小节首先对摩擦力的加载进行理论推导.
制动区域摩擦作用点的摩擦功W与摩擦线速度v成正比.因为
v=ωr
则有:
W∝r
设比例系数为k2,因此公式可改写为
W=k2r
(11)
所以只需要计算出k2值就能较为准确的求解制动区域每一摩擦作用点的摩擦功Wi.
由于制动过程中整个制动区域每一时刻的总摩擦功
=k2r1+k2r2+…+k2ri+
(12)
其中,n为此有限元模型中制动区域在该时刻的有效摩擦面积上的节点数.
将式(12)适当变形从而求得比例系数
(13)
将式(13)代入(11)最终得到每一摩擦作用点的摩擦力
(14)
3 基于速度梯度循环法的热-结构耦合的算例分析
以某型号兆瓦级风电制动器的结构为例,制动闸片的材料为铜基粉末冶金复合材料.在有限元计算分析中,使用ANSYS中APDL模块编写相应命令流,实现材料属性边界条件的施加,其中制动盘制动过程的初始转速为2 000 r/min,施加制动压力载荷为17 000 N.基于速度梯度循环法编写热流密度加载函数,在制动闸片顶面施加制动载荷,然后通过函数加载的方式施加制动闸片底面摩擦区域的摩擦热流,设置载荷步进行热分析,之后将前面生成的温度场中的热单元转化成结构单元,加载摩擦载荷,最后将热分析生成的*.rth文件作为体载荷加载到制动闸片结构分析文件上,时间步长及其加载时间通过全局命令流控制.分析计算所需材料参数如表1所示.
图2为制动闸片的约束条件及载荷施加示意图,根据实际工况要求假设制动盘逆时针转动,以仿真坐标系作为参考坐标系,由上一部分对边界条件的分析可知制动闸片左侧凹槽表面受X,Z方向的约束、底而受Y方向约束,并在如图2所示表面施加压力及模拟施加热流密度及摩擦力.图3表示了热-结构耦合理论流程.
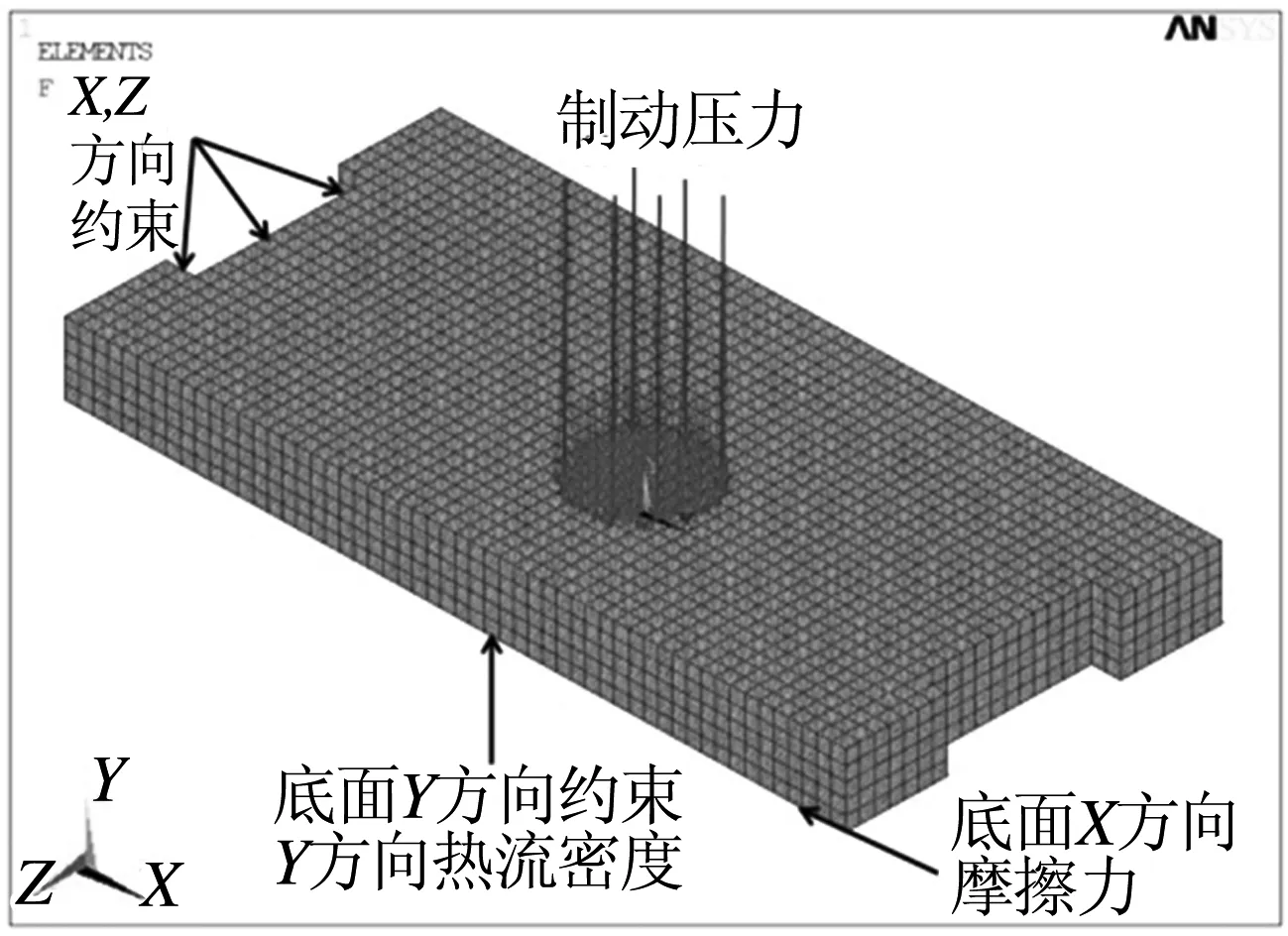
图2 制动闸片的约束条件及载荷示意图
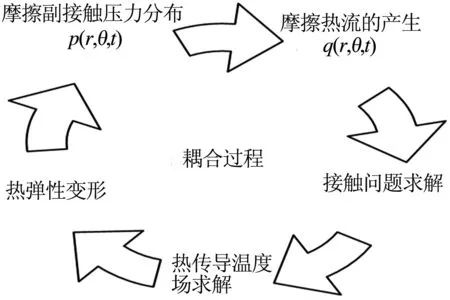
图3 热-结构耦合过程示意图
根据以上理论、边界条件、有限元模型、计算公式,采用ANSYS求解器对制动器制动过程温度场进行计算,得到制动闸片的温度场、结构场分布.
3.1 制动器闸片的温度场分布特性
图4为采用速度梯度循环法加载的制动闸片在制动过程结束即19.16 s时的瞬态温度场分布云图,从图4(a)可以看出,制动过程中制动闸片温度分布不均匀,以图中右侧为Z轴正向则闸片等温线向右侧倾斜即呈“左高右低”分布且闸片温度值也服从“左高右低”的分布规律,图4(b)闸片底面高温区集中在沿制动盘半径方向的外侧(图中为Z轴负向),温度最大值分布在在闸片底面远离制动盘旋转中心的端点处.
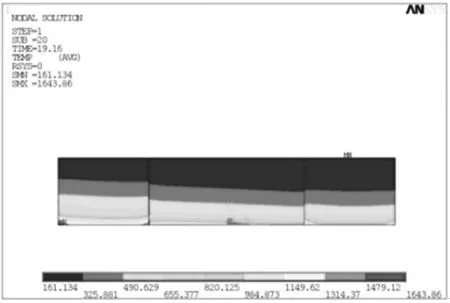
(a) 闸片左侧面
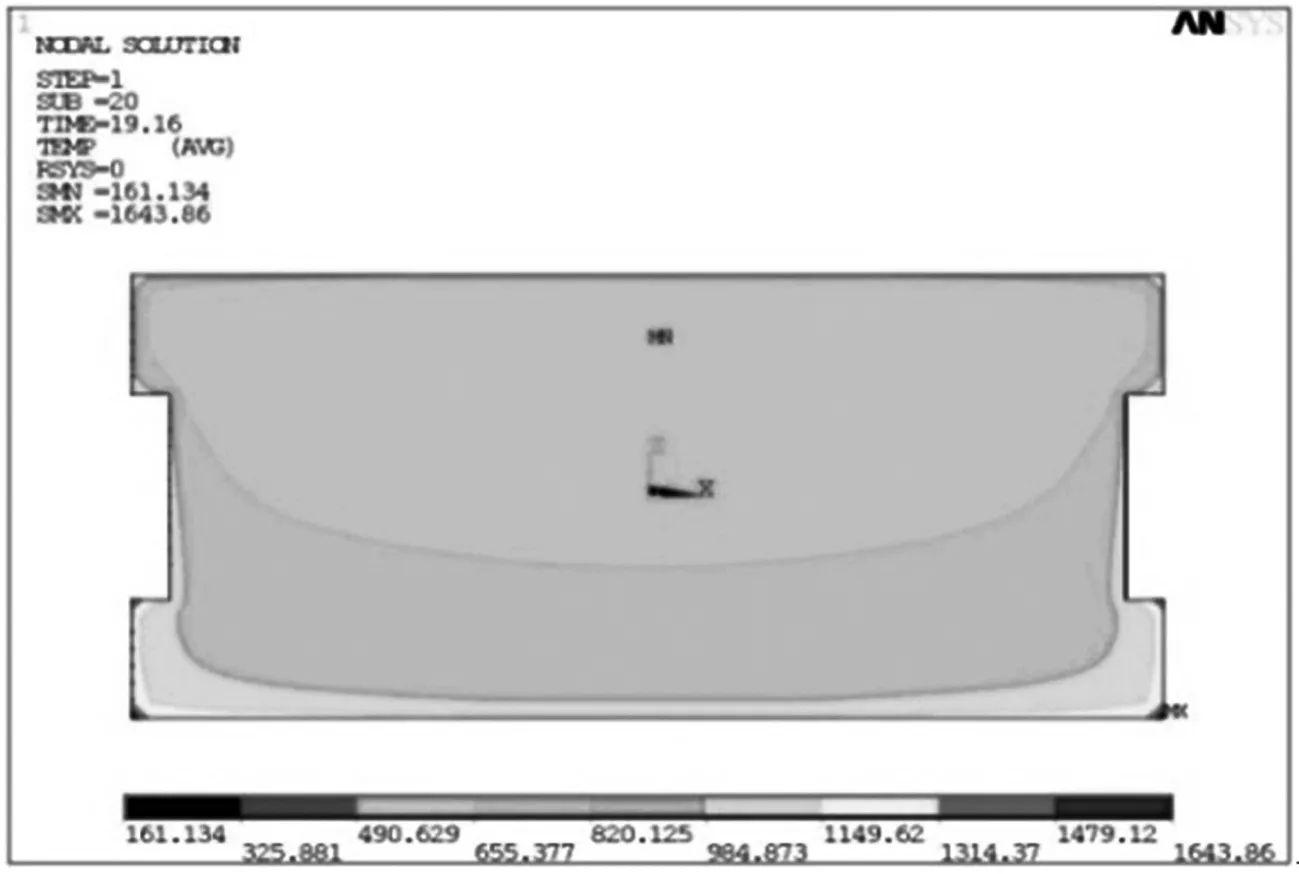
(b) 闸片下底面
制动过程产生的摩擦热流作用于闸片底面并向闸片厚度方向传热,但摩擦热流在底面分布是不均匀的,由于闸片沿制动盘半径方向的外侧线速度大于内侧,而线速度大往往导致摩擦热作用明显并且产生热流大,所以外侧温度高于内侧温度.
3.2 制动器闸片的应变分布特性对比分析
由于在建模过程中对闸片的位移约束施加在如图2所示方向,所以图5所示制动闸片下底面合位移分布云图中闸片沿X轴方向的变形左侧大于右侧,图5(a)为采用平均热流密度分布法加载的制动闸片在19.16 s时的瞬态温度场分布及闸片在制动器位移分布云图,与图5(b)采用速度梯度循环法的云图对比,可以发现两图制动闸片应变均沿制动盘相对运动方向增大并沿制动盘径向递增,最大变形区域集中在沿X轴正方向的右侧,但在沿制动盘半径方向图5(b)比图5(a)变化趋势明显,并且图5(b)应变变化区域呈由X轴偏向Z轴方向的波浪线分布.

(a) 闸片左侧面

(b) 闸片下底面
闸片在X轴方向受到位移约束,其摩擦应变由远离约束端到靠近约束端递减;又因为闸片沿制动盘径向的摩擦线速度递增使单位面积产生的热流密度递增,闸片底面高温区集中在沿制动盘半径方向的外侧,由于耦合作用的存在,使闸片摩擦应变沿X轴正向偏向Z轴负向递增.这也验证了使用速度梯度循环法与传统均匀加载方法相比的准确性.
3.3 制动器闸片的应力分布特性对比分析
图6为制动闸片在19.16 s时的等效应力分布云图,其分别采用均匀加载法如图6(a)和速度梯度循环法如图6(b)加载.由于闸片主要受作用于闸片顶面的压力载荷和底面与制动盘摩擦产生的摩擦力,将速度梯度循环法与均匀加载方法相比较,可以看出采用速度梯度循环法加载处理后,闸片底面的等效应力分布沿制动盘方向由内向外递增.由于制动器实际制动过程中制动盘逆时针旋转而闸片左侧面受到导轨的约束,制动盘、闸片摩擦作用产生的应力集中在闸片的左侧,又因为沿制动盘半径方向速度梯度的存在,从而导致外侧摩擦作用更为明显,而速度梯度循环法可有效模拟该工况,使仿真分析结果与实际相一致.
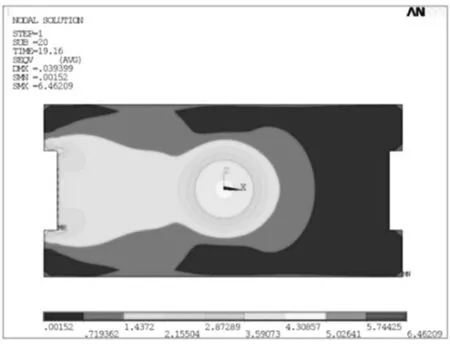
(a) 采用均匀加载方法
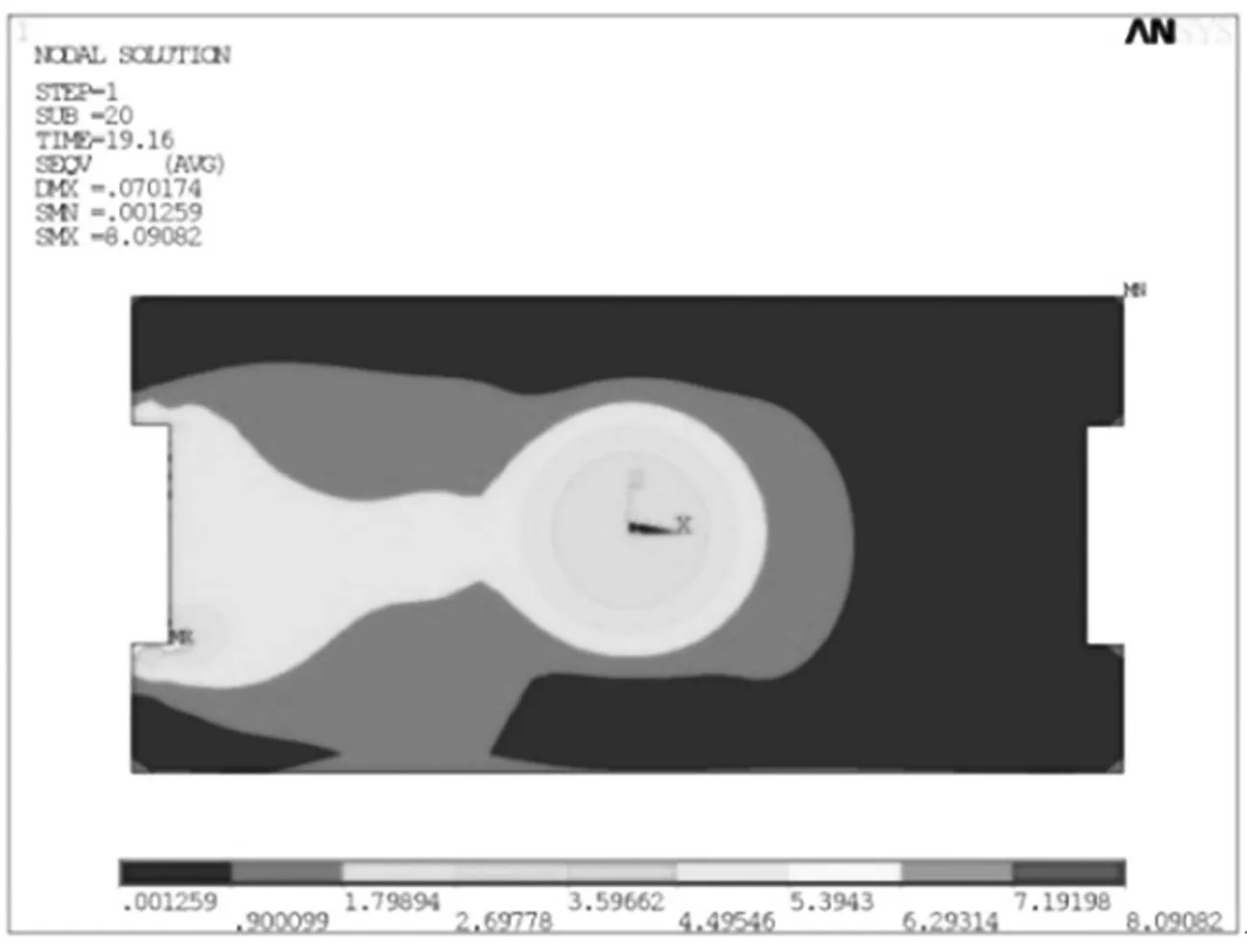
(b) 采用速度梯度循环法
结合图4,沿制动盘半径方向制动闸片摩擦面外侧材料累积的热量高于材料内侧,因此闸片外侧温度明显高于内侧温度,从而在制动盘径向产生温度变化梯度,这一温度梯度使得制动闸片摩擦区域变形要向径向扩展,但受到非温升的约束而不能自由进行,导致闸片在摩擦高温区域沿制动盘径向产生了很大的压应力.
由于闸片沿制动盘半径方向(图中为Z轴负向)等效应力分布靠向外侧,又有外侧线速度大于内侧,而底面高温区又分布在外侧,由摩擦学相关理论[11]可推测出制动闸片底面材料的磨损在外侧要比内侧严重.
4 结论
本文基于大兆瓦风电制动器制动摩擦副的结构特性,考虑作用于制动闸片的相对线速度径向差异及其影响下的摩擦热流与应力的耦合过程,提出速度梯度循环法,并推导出热流密度的加载式,建立了大兆瓦风电制动器三维热-结构耦合瞬态有限元模型对制动闸片热-结构耦合过程进行分析.得出以下结论:
(1)在风电制动器制动过程中,制动闸片的温度场与应力场之间存在耦合关系,使用速度梯度循环法可有效模拟实际工况.并得出制动闸片摩擦区域沿制动盘半径方向呈现出弧度明显的等温带且温度梯度沿半径尺寸增大方向递增,较准确的反应制动过程中闸片温度场与应力应变分布特性;
(2)制动闸片沿制动盘半径尺寸方向外侧温度明显高于内侧温度,从而闸片在制动盘半径方向产生温度梯度,导致闸片在摩擦高温区域沿制动盘径向产生了很大的压应力.且通过以上分析得出制动闸片摩擦表面的磨损沿制动盘半径增大方向外侧比内侧严重.
[1]黄健萌, 高诚辉. 盘式制动器热-结构耦合的数值建模与分析[J].机械工程学报, 2008(2):145-151.
[2]KWANGJIN L, BARBER JR. Frictionally excited thermoelastic instability in automotive disk brakes[J]. ASME Journal of Tribology, 1993, 115: 607-614.
[3]ZAGRODZKI P, LAM KB, BAHKALI EA, et al. Nonlinear transient behavior of a sliding system with frictionally excited thermoelastic instability[J]. ASME Journal of Tribology, 2001, 123:699-708.
[4]BOLK H. The flash temperature concept[J]. Wear, 1963, 6:483-493.
[5]EVTUSHENKO OO, IVANYK EH, HORBACHOVA NV. Analytic methods for thermal calculation of brakes(review)[J]. Materials Science, 2000, 36 (6):857-862.
[6]华林, 向上升.汽车气压盘式制动器瞬时温度场研究[J].润滑与密封, 2007, 32(5): 8-11.
[7]王新波.风电制动器的热-结构耦合分析[D]大连:大连理工大学, 2010.
[8]马保吉, 朱均.摩擦制动系统摩擦表面的摩擦学研究[J].机械科学与技术, 1999(1):14-16.
[9]胡育勇.风机主轴制动器摩擦副热-力耦合有限元分析[D].南昌:南昌大学, 2014.
[10]刘建秀.铜基粉末冶金摩擦材料研制及其高温疲劳磨损和冲击性能研究[D].河南:中国工程物理研究院, 2003.
[11]温诗铸.摩擦学原理[M].4版,北京:清华大学出版社, 2012.
Study on Coupling Analysis of Thermal-Structure for Megawatt Wind Turbine Brakes
SHA Zhihua, LIU Nan, LIU Yu, MA Fu Jian, YIN Jian, ZHANG Shengfang
(School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028)
In view of the braking process for megawatt wind turbine brakes and considering the effects that the width of brake friction area and linear velocity radial difference, the gradient of velocities circulation method is put forward, and the thermal-structure for the brake in braking process is analyzed. First, the model of three dimensional transient heat transfers for brake friction pair is build based on ANSYS. Then heat flowing density is loaded by the gradient of velocities circulation method. At last, geometrical parameters are determined, and the loading function of heat flowing density is plugged. The result of temperature field analysis in the disc brake friction slice of temperature radius direction presents a radian obvious temperature zone. Direction of increased temperature gradient along the radius size is reduced. Using gradient of velocities circulation method integrated the results of thermal analysis generation into the structure under coupling analysis of force and deformation analysis of brake friction slice, wear condition can be forecasted. Compared with traditional uniform loading method using the analysis of the velocity gradient method is closer to the actual results. The analysis method provides the reference for simulation of the large size disc brake friction braking condition process.
wind turbine brakes; thermal-structural coupling; gradient of velocities circulation method; finite element simulation
1673- 9590(2016)06- 0066- 06
2016-06-03
国家自然科学基金资助项目 (51475066); 辽宁省自然科学基金资助项目(2015020114); 辽宁省教育厅优秀人才计划资助项目(LR2015012)
沙智华(1973-),女,教授,博士,主要从事CAD/CAM/CAE,机械结构优化设计方面
A
E- mail:zhsha@djtu.edu.cn.
