携能通信协作认知网络稳态吞吐量分析和优化
2016-12-20阔永红贺冰涛
阔永红,贺冰涛,陈 健
(西安电子科技大学 通信工程学院,陕西 西安 710071)
携能通信协作认知网络稳态吞吐量分析和优化
阔永红,贺冰涛,陈 健
(西安电子科技大学 通信工程学院,陕西 西安 710071)
在携能通信协作认知网络中,针对主用户和认知用户的非饱和数据传输问题,研究主用户网络和认知用户网络稳态吞吐量之间的相互作用关系,并对认知网络进行稳态吞吐量的优化.首先,提出一种“概率协作”的传输策略,采用排队论的方法对该场景进行网络层建模和分析,求解出系统的稳态吞吐量域,并以此反映主用户网络和认知用户网络的相互作用关系.其次,通过求解“概率协作”策略中认知用户的最优协作传输概率,在保证主用户系统稳定的情况下,最大化认知用户的稳态吞吐量.仿真结果和分析表明,采用“概率协作”的传输策略能使认知用户获得最大的稳态吞吐量,同时,主用户网络相比于无协作时的系统性能也有了较大的提升.
携能通信;认知无线电;协作通信;稳态吞吐量
协作认知无线电网络(Cooperative Cognitive Radio Network, CCRN)中认知节点通过对授权节点协作与授权网络共享频段,是一种高频谱利用率的双赢通信技术[1-2].然而,在现实中充当协作中继的认知用户并不是充足供能的基站,而是一些低功耗的节点[3],这些节点由于仅装载储能有限的电池进行通信,很大程度上制约了网络的生存时间[4].基于携能通信的协作认知网络[3]在传统的CCRN中采用无线携能通信技术(Simultaneous Wireless Information and Power Transfer, SWIPT),可使认知用户在感知和接收主用户射频信号的同时,通过能量回收技术(Energy Harvesting, EH)从承载信息的无线电射频信号中获得传输能量,实现能量与信息的并行传输,可有效解决CCRN中节点能量受限的问题,延长节点生存时间,为进一步提升谱效和能效提供了有效的手段.
在采用携能通信技术的CCRN中已有大量文献[3,5-6]采用香农容量来表征系统的最大可达速率,并以此来衡量和分析系统性能.在实际的数据传输中主用户和认知用户并非时刻都有数据需要传输,即数据包的产生时刻和传输持续的时间具有不确定性,这使得用户缓存器中的数据包队列是非饱和的,而采用香农容量并不能描述在该情况下系统的长程性能(队列的稳定性及时延等[7]).针对数据的非饱和传输问题,文献[8]在基于携能通信认知网络中采用排队论的方法进行了网络层的系统性能优化,在保证主用户系统稳定的同时,通过优化认知网络的传输概率使认知网络的稳态吞吐量最大化.然而,该研究并未涉及主用户与认知用户间的相互协作.针对协作通信中非饱和数据传输问题的研究,文献[9]在三节点的携能通信协作中继网络中,分析了中继节点能量收集与数据包协作传输间的切换对系统性能的影响.文献[2,10]在传统的CCRN中分别对单认知用户节点和多认知用户节点的协作场景,通过稳态吞吐量域直观反映了该多接入网络中,主用户稳态吞吐量和认知用户稳态吞吐量之间的相互作用关系.在采用携能通信的CCRN中,认知用户的稳态吞吐量不仅会受到主用户业务传输强度的影响,同时也会受到自身传输能量的制约.一方面,随着主用户传输的频繁,认知用户可以更多地从主用户传输的信号中获得传输能量用于自身的数据传输,但主用户频繁占用信道使得认知用户的传输机会减少; 另一方面,由于认知用户对主用户的协作增大了认知用户的传输机会,但同时认知网络又要消耗部分的能量进行协作传输.因此,在非饱和通信情况下,对携能通信的CCRN的稳态吞吐量的分析,需要联合考虑主用户活动、认知用户能量状态及认知用户的传输机会.
综上所述,针对携能通信的协作认知网络中的非饱和数据通信问题,笔者分析主用户网络和认知用户网络稳态吞吐量之间的相互作用关系,并最大化认知网络系统的稳态吞吐量,使认知网络能够承载较高的数据包到达率.首先,在该场景中提出一种部分协作策略[11],即对主用户进行概率性的协作,并采用排队论求解出该系统的稳态吞吐量域,来反映主用户网络和认知用户网络稳态吞吐量之间的相互作用关系; 其次,在保证主用户网络队列稳定的前提下,通过求解最优协作概率c,使认知网络的稳态吞吐量最大化; 最后,通过仿真分析了在不同协作策略下系统的稳态吞吐量域,及不同能量转化效率对系统性能的影响.
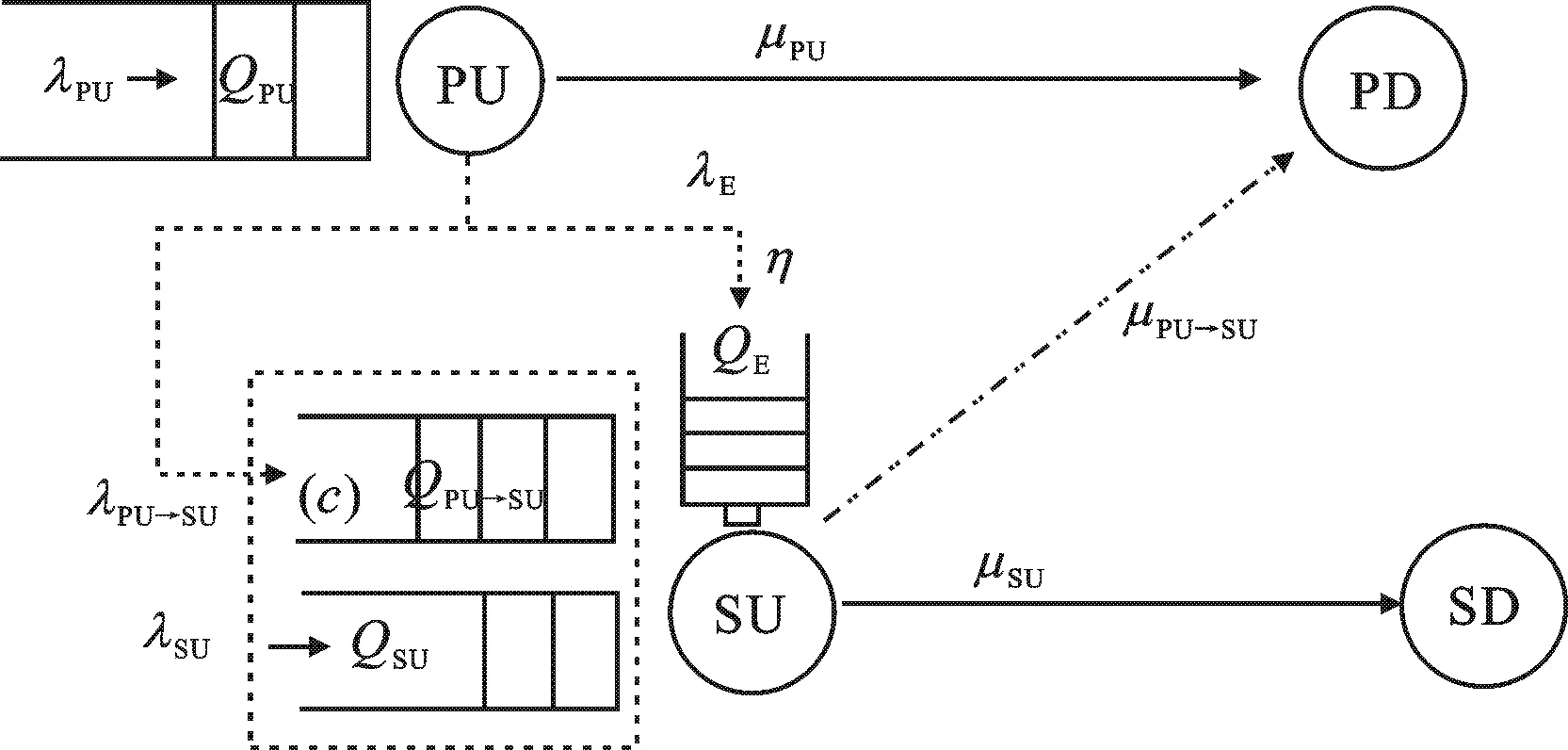
图1 系统模型
1 系统模型
在图1所示的系统中,由主用户基站PU、主用户接收端PD和认知用户节点SU、认知用户接收端SD构成.图中PU有1个无限长缓存器QPU,用来存储主用户随机到达的等长数据包.SU有2个无限长缓存器,QPU→SU用来存储主用户目的端PD未成功接收而SU成功接收的主用户数据包;QSU用来储存认知用户随机到达的等长数据包.QPU、QSU中数据包的到达过程均为伯努利过程.PU为能量非受限节点,SU仅通过射频能量回收技术从PU发送的射频信号中获取能量,并储存在无限长的能量储存装置QE中,其能量的转化效率为η[8].
主用户和认知用户的信道接入方式设定如下[8,10]:
(1) 当主用户有数据传输时(缓存器QPU的数据包队列非空)会占用授权信道进行传输,认知用户只能在未被主用户占用的时段内进行数据传输.
(2) 主用户或认知用户的目的端成功接收到各自用户发送的信息后,会通过完美的反馈信道来广播ACK应答消息; 若未成功接收,则广播NACK,且在下一个时隙内进行数据包的重传.
(3) 对主用户目的端未成功接收到的数据包,若该数据包能成功被认知用户接收,认知用户可选择不协作而直接将该数据包丢弃,此时主用户需进行重传.也可选择协作主用户重传,将该数据包储存在协作缓存器QPU→SU,并等待空闲时刻传出,此时主用户会将该传输失败的数据包从队列中移除不重传该数据包.
(4) 认知用户的传输包含两个缓存器的传输(QPU→SU、QSU),当认知用户获得空闲时间进行数据传输时,要优先传输储存在节点中主用户的数据,即只有当协作缓存器QPU→SU中没有数据包时才可传输自己的数据包.同时认知用户能量受限,因此,只有当能量储存装置QE非空时,才能进行数据传输.
(5)pPU→PD、pPU→SU、pSU→PD、pSU→SD分别表示主用户PU数据包成功被目的端PD接收的概率、主用户PU数据包成功被认知用户SU接收的概率、储存在QPU→SU中的数据包成功被主用户目的端PD接收的概率、认知用户自身数据包成功被认知用户目的端SD接收的概率.
笔者将一个等长数据包传输的时间作为一个时隙,且一个数据包传输所消耗的能量为一个单元块,相比于传输所消耗的能量,可忽略感知和信号处理所消耗的能量[12].
2 稳态吞吐量的建模和分析
本节对携能通信的协作认知网络的系统稳定性进行分析,并求出系统的稳态吞吐量域.由Loynes定理可得系统能够处于稳定状态的条件:
其中,λPU、λPU→SU和λSU分别为主用户数据包的到达率、协作数据包的到达率和认知用户数据包的到达率;μPU、μPU→SU和μSU分别为主用户数据包的服务率、协作数据包的服务率和认知用户数据包的服务率.主用户和认知用户的最大稳态吞吐量可定义为满足系统稳定性条件下,主用户节点和认知用户节点所分别能承载的数据包的最大到达强度,即λPU及λSU的上界.系统的吞吐量域为所有满足系统稳定条件的服务率对(λPU, λSU)所组成的集合.下面针对主用户网络和认知用户网络分别求出μPU和μSU及系统的吞吐量域.
2.1 主用户网络
在该协作场景中,主用户网络的平均服务率μPU可表示为
当PU发送的数据包未能被PD成功解码而被SU成功解码后,SU可以概率c选择协助主用户传输该数据包.c ∈ [0,1],当c取0时,表示认知用户不协助主用户;当c取1时,表示认知用户完全对主用户进行协作.认知用户通过协作可尽快清空主用户队列为认知用户创造更多传输机会,但由于节点的能量受限,使得一部分空闲时间并不能被用来传输认知用户的数据.因此,在下一节会对c进行优化,使认知用户的传输能量和传输机会达到最优折中.
主用户的数据包的到达率为λPU,则主用户占用信道的概率UPU可以表示为主用户队列QPU非空的概率,由Little定理可得
2.2 认知用户网络
认知用户网络的平均服务率μSU可表示为
其中,Pr[QPU=0]=1-UPU.为求得认知用户协作缓存器中队列为空的概率Pr[QPU→SU=0],应求出协作缓存器中数据包的到达率λPU→SU及服务率μPU→SU.
其中,ψ表示数据包未成功被PD接收,但成功被SU接收事件;Pr[QE≠ 0]为认知用户能量队列非空概率,即认知用户有能量进行传输的概率.由于认知用户是通过主用户发射的信号获取能量,在一个时隙内可接收到单位能量的概率为UPU.认知用户的能量到达率 λE= UPUη,η为能量转化效率,认知用户能量队列非空的概率Pr[QE≠ 0]可由文献[13]得到:
综上可得,认知用户网络的平均服务率μSU为
2.3 系统稳态吞吐量域
由系统的稳定条件可得系统的稳态吞吐量域为
其中,Δ=c pPU→SU(1-pPU→PD).在该系统中主用户网络所能达到的最大稳态吞吐量受协作概率c的影响,认知用户可达到的最大稳态吞吐量由主用户的业务传输强度(数据包到达率λPU)、协作概率c和能量转化率η共同决定.对于固定能量转化率的认知用户为使其能达到最优的性能,需要根据主用户的传输行为来自适应地调整自己的协作策略,从而最大化自身的稳态吞吐量.
3 协作概率优化
由上述分析,下面在保证主用户队列稳定的前提下,通过优化协作概率c,最大化认知网络的稳态吞吐量,即
将式(10)写为有关λPU和λSU的表达式为
分别将F(1)、F(2)对c求导,有
通过求导可知,F(1)为单调递减函数,F(2)的增减性只取决于pPU→PD和pSU→PD的关系.下面针对 pPU→PD> pSU→PD和 pPU→PD≤ pSU→PD两种情况分别对最优的协作概率c进行求解.
(1) pPU→PD>pSU→PD: 主用户自身传输成功的概率高于认知用户协助传输成功的概率,此时λPU的取值范围为(0,pPU→PD).F(1)、F(2)均为单调递减函数,在该条件下最大化问题即为根据约束条件求c的下界.将约束条件式(11b)、(11c)和式(11d)写为如下形式:
对于任意的λPU∈(0,pPU→PD),由式(14a)与式(14d)可求得c的下界为负数,又 c ∈ [0,1],最优的协作概率c均为其下界取值0.这表明当主用户自身传输成功的概率高于认知用户协助传输成功的概率时,为使认知用户稳态吞吐量最大化,认知用户不应当对主用户进行协作.这是因为,虽然认知用户对主用户协作能尽快清空主用户的数据包使认知用户获得更多的频谱接入时间,但在空闲的时间内认知用户要优先传输主用户未能成功传输的数据包,而认知用户协作主用户重传所耗费的时间却高于主用户自身重传所耗费的时间,这样一方面使得认知用户传输自己数据包的机会减小,另一方面,使认知用户只能用更少的能量来传输自身数据包.
(2) pPU→PD≤pSU→PD: 即认知用户协助传输成功的概率高于主用户自身传输成功的概率,此时λPU的取值范围为(0,pSU→PD).F(1)为单调递减函数,F(2)为单调非减函数,μSU的最大值可在F(1)和F(2)的交点处取得.令 F(1)= F(2),可求得交点处对应的协作概率c,记作cst1.
在该条件下μSU的最大化问题,需根据约束条件求c的取值范围并判断cst1与c的取值范围的关系来求解最优的协作概率c.将约束条件式(11d)化简,可得
不等式(16)左右两边的正负性会受到λPU取值的影响从而使c的取值范围发生变化,下面将在λPU不同的取值区间分别对最优的协作概率c进行求解.
(1) 当pSU→PD> λPU>pPU→PD时,可将约束条件式(11b)、(11c)和式(11d)写为如下形式:
为保证系统稳定,应有cst3> cst2,cst3> cst4,由此可得
可由约束条件求得c的上界为min(cst3,1),c的下界为max(0,cst2,cst4).当交点cst1大于c的上界时,最优的c应取上界; 当交点cst1处于c取值范围内时,最优的c应取交点cst1; 当交点cst1小于c的下界时,最优的c应取下界.在该条件下的最优协作概率c可表示为
(2) 当pPU→PD≥λPU时,可将约束条件式(11b)、(11c)和式(11d)简化为如下形式:
同理可得,在该条件下的最优协作概率c为
认知用户的最优协作概率受主用户的传输和能量转化率的联合约束,下面结合仿真结果做具体分析.
4 仿真结果与分析
从上面的分析中可知,在pPU→PD>pSU→PD时,认知用户最优的协作概率恒为0.为研究协作对系统性能的影响,下面将对主用户传输成功概率低于认知用户协助传输成功概率 (pPU→PD≤ pSU→PD)的情况进行仿真.不同传输路径下数据包成功传输的概率假设如下: pPU→PD= 0.5,pPU→SU= 0.8,pSU→PD= 0.9,pSU→SD= 0.8[2].
图2给出了在能量转化率η=0.8时,不同协作策略下系统稳态吞吐量域.图3给出了在能量转化率 η=0.8 时,不同协作策略下主用户未占用信道的概率和认知用户能量非空的概率曲线.从图2中可看出,采用最优协作概率的“概率协作传输”策略相比于无协作传输和完全协作传输策略有更大的稳态吞吐量域.
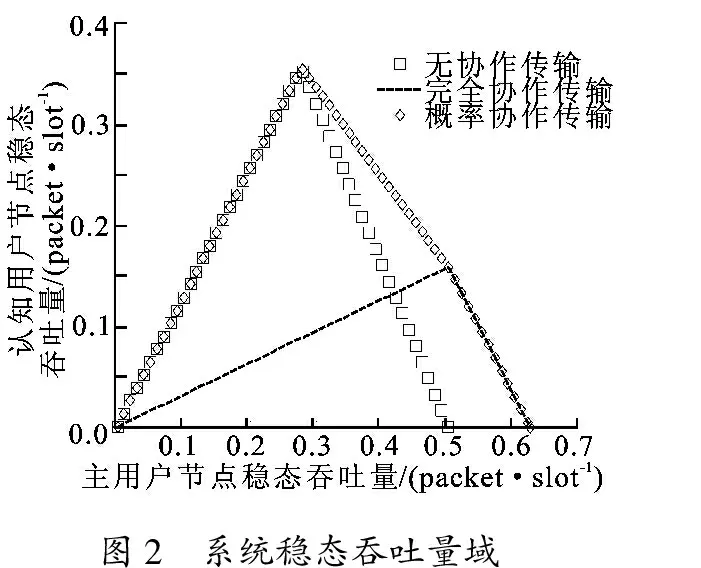
图2 系统稳态吞吐量域
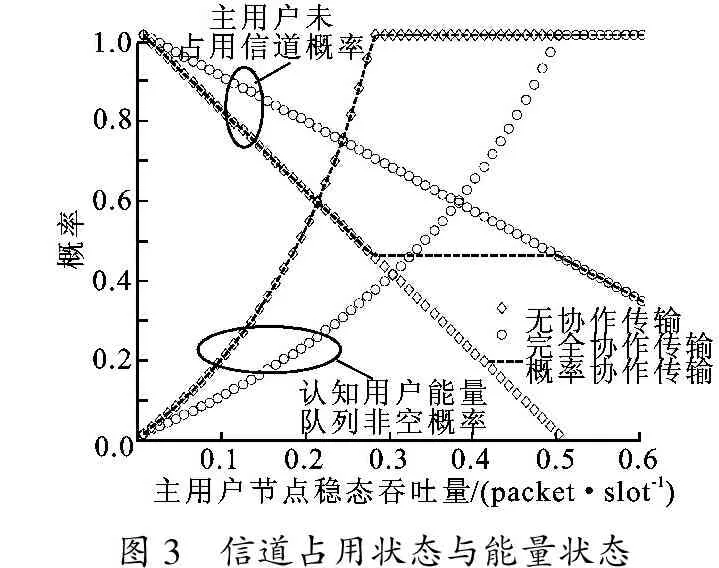
图3 信道占用状态与能量状态
结合图2和图3进行分析,当λPU≤0.28(式(22)中cst1≤0)时,“概率协作传输”策略的最优协作概率为0,即“无协作传输”.由图3可知,此时认知用户虽有大量传输机会,但认知用户可获得的射频能量较少导致系统稳态吞吐量较低.当λPU由0.00增大到0.28时,认知用户损失了部分传输机会,却获得更多能量用于自身数据包传输,使认知用户的吞吐量逐渐上升.当λPU继续增大时,认知用户可获得的传输能量逐渐趋于饱和态,即能量队列中总有剩余能量,但主用户更多地占用信道却使认知用户的传输机会大幅减少.“概率协作传输”策略将以一定的概率协作主用户清空主用户队列,“完全协作传输”策略相比于“概率协作传输”策略可使认知用户获得更多传输机会,但一方面使认知用户从主用户信号中获得总能量的频率减少,另一方面却需消耗更多能量进行协作传输.“概率协作传输”策略通过动态调整认知用户的协作概率,将认知用户的传输能量和传输机会很好地折中.当 λPU≥ 0.5时,认知用户最优协作概率为1,即“完全协作传输”.
图4给出了不同能量转化率下认知用户的最优协作概率取值.图中λPU的取值受到式(11)的约束,因此,在不同能量转化率下的可取的最大值不同.当能量转化率较低 (η= 0.1,η= 0.4)时,认知用户的最大协作概率均不能达到1,即不能采用“完全协作传输”策略,这是由于在较低的能量转化率下认知用户获得的能量较少,认知用户只能对主用户传输失败的部分数据包进行协作.若对主用户传输失败的所有数据包都进行协作,则会使认知用户的服务率小于数据包的到达率,不能满足QPU→SU队列的稳定条件.从图中可看出,随η的增大,c的曲线会在更小的λPU下有数值且以更快的速度增长到1.这是由于在较高的能量转化率下,认知用户在较小的λPU便可获得较为充足的能量, 因此, 可以将一部分能量用来协助主用户传输, 尽快清空主用户的数据包,使自身获得更多传输机会,并利用协作所获得的传输机会来传输自身的数据包.

图4 不同能量转化率下的协作概率

图5 不同能量转化率下的系统稳态吞吐量域
图5给出了采用概率协作策略时,不同能量转化率下的系统稳态吞吐量域.能量转化率越高,系统可获得的吞吐量域越大.但从图中可看出,认知用户的稳态吞吐量增加的幅度越来越小.在较低的能量转化率下,增大能量转化率意味着认知用户有更多的能量来传输自己的数据包,但随着转化率的不断增大,传输机会的限制使得认知用户并不能将收集到的全部能量用于自身的数据传输.
5 结 束 语
在携能通信协作认知网络中考虑更为实际的非饱和通信,对该系统进行网络层的建模分析.通过求解该系统的稳态吞吐量域直观反映主用户和认知用户吞吐量之间的相互影响.针对认知用户的传输机会和能量之间的折中问题,提出概率协作传输策略最大化认知用户的稳态吞吐量.通过仿真分析,在保证主用户队列稳定的前提下,采用“概率协作”传输策略的系统的性能优于“无协作传输”和“完全协作传输”策略; 增大能量转化效率可提升认知用户的稳态吞吐量,但这种影响会随着能量转化率的增大而减弱.
[1] CAO B, MARK J W, ZHANG Q Y, et al. On Optimal Communication Strategies for Cooperative Cognitive Radio Networking [C]//Proceedings of IEEE International Conference on Computer Communications. Piscataway: IEEE, 2013: 1726-1734.
[2]KOMPELLA S, NGUYEN G D, WIESELTHIER J E, et al. Stable Throughput Tradeoffs in Cognitive Shared Channels with Cooperative Relaying [C]//Proceedings of IEEE International Conference on Computer Communications. Piscataway: IEEE, 2011: 1961-1969.
[3]ZHENG G, HO Z, JORSWIECK E A, et al. Information and Energy Cooperation in Cognitive Radio Networks [J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2290-2303.
[4]LIU L, ZHANG R, CHUA K C. Wireless Information Transfer with Opportunistic Energy Harvesting [J]. IEEE Transactions on Wireless Communications, 2013,12 (1):288-300.
[5]WANG Z H, CHEN Z Y, LUO L, et al. Outage Analysis of Cognitive Relay Networks with Energy Harvesting and Information Transfer [C]//2014 IEEE International Conference on Communications. Piscataway: IEEE Computer Society, 2014: 4348-4353.
[6]KRIKIDIS I, TIMOTHEOU S, NIKOLAOU S, et al. Simultaneous Wireless Information and Power Transfer in Modern Communication Systems [J]. IEEE Communications Magazine, 2014, 52(11): 104-110.
[7]SADEK A K, LIU K J R, EPHREMIDES A. Cognitive Multiple Access via Cooperation: Protocol Design and Performance Analysis [J]. IEEE Transactions on Information Theory, 2007, 53(10): 3677-3696.
[8]LU Y, WANG W, ZHANG Z Y, et al. Random Access for a Cognitive Radio Transmitter with RF Energy Harvesting [C]//2014 IEEE Global Communications Conference. Piscataway: IEEE, 2014: 923-928.
[9]KRIKIDIS I, TIMOTHEOU S, SASAKI S. RF Energy Transfer for Cooperative Networks: Data Relaying or Energy Harvesting? [J]. IEEE Communications Letters, 2012, 16(11): 1772-1775.
[10]FANOUS A, EPHREMIDES A. Stable Throughput in a Cognitive Wireless Network [J]. IEEE Journal on Selected Areas in Communications, 2013, 31(3): 523-533.
[11]PAPPAS N, JEON J, EPHREMIDES A, et al. Wireless Network-level Partial Relay Cooperation [C]//Proceedings of IEEE International Symposium on Information Theory. Piscataway: IEEE, 2012: 1122-1126.
[12]JEON J, EPHREMIDES A. On the Stability of Random Multiple Access with Stochastic Energy Harvesting [J]. IEEE Journal on Selected Areas in Communications, 2015, 33(3): 571-584.
[13]KASHEF M, EPHREMIDES A. Optimal Partial Relaying for Energy Harvesting Wireless Networks [J]. IEEE/ACM Transactions on Networking, 2016, 24(1): 113-122.
(编辑:李恩科)
Stable-throughput analysis and optimization of cooperative cognitive radio networks based on information and energy cooperation
KUOYonghong,HEBingtao,CHENJian
(School of Telecommunications Engineering, Xidian Univ., Xi’an 710071, China)
According to the unsaturated data traffic in wireless communications, this paper studies the interaction between primary users (PUs) and secondary users (SUs) in a cooperative cognitive radio network which is based on information and energy cooperation, and optimizes the stable-throughput of SUs. A probabilistic cooperation scheme has been proposed and the stable-throughput region has been characterized in order to reflect the interaction between PUs and SUs by using the Queuing Theory. Then by deriving the optimal value of the relaying probability, the stable-throughput of secondary users can be maximized under the constraint of the primary queue stability. Simulation results and theoretical analysis show that the probabilistic cooperation scheme can achieve maximal stable-throughputs for SUs, and meanwhile PUs can also have a better performance compared to the non-cooperative case.
simultaneous wireless information and power transfer;cognitive radio;cooperative communication;stable-throughput
2015-06-27
时间:2016-04-01
国家自然科学基金资助项目(61440056);高等学校学科创新引智计划资助项目(B08038)
阔永红(1967-), 女,教授,博士,E-mail:yhkuo@mail.xidian.edu.cn.
http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.002.html
10.3969/j.issn.1001-2400.2016.06.001
TN92
A
1001-2400(2016)06-0001-07
