贝叶斯非线性混合效应模型及其应用研究
2016-12-20王明高孟生旺
王明高,孟生旺
(1.山东工商学院 统计学院,山东 烟台 264005; 2.中国人民大学 应用统计科学研究中心,北京100872)
【统计理论与方法】
贝叶斯非线性混合效应模型及其应用研究
王明高1,2,孟生旺2
(1.山东工商学院 统计学院,山东 烟台 264005; 2.中国人民大学 应用统计科学研究中心,北京100872)
由于常用的线性混合效应模型对具有非线性关系的纵向数据建模具有一定的局限性,因此对线性混合效应模型进行扩展,根据变量间的非线性关系建立不同的非线性混合效应模型,并根据因变量的分布特征建立混合分布模型。基于一组实际的保险损失数据,建立多项式混合效应模型、截断多项式混合效应模型和B样条混合效应模型。研究结果表明,非线性混合效应模型能够显著改进对保险损失数据的建模效果,对非寿险费率厘定具有重要参考价值。
混合效应模型;非线性模型;保险损失;贝叶斯
一、引 言
混合效应模型在教育、医学、社会和金融保险等领域具有广泛的应用价值。很多保险数据需要进行分层分析,比如同一地区的车辆和房屋等保险标的都具有相似的风险特征,而不同地区的这些保险标的具有一定的差异性,这些保险标的的损失数据都不满足相互独立的假设条件。对于不满足独立性假设并具有层次性的纵向数据,普通的回归模型将不再适合,而考虑数据间的相关性和层次性的混合效应模型既含有固定效应参数,又含有随机效应参数,能够更好地分析纵向数据。混合效应模型的核心思想是通过在模型中加入随机效应,来体现组内数据的相关性和不同组数据的异质性。对于观察数据比较少的个体,混合效应模型的推断结果会产生向平均值聚集的倾向,从而得到更加稳健的估计结果[1-2]。
线性混合效应模型假设变量之间存在简单的线性关系。为了描述变量之间的非线性关系,需要借助于非线性混合效应模型,该模型能够很好地处理同一个体重复观测数据的相关性以及变量之间的非线性关系。多项式在非线性回归模型中较常使用,但其缺陷是,当多项式的阶数较低时模型的拟合效果不佳,而增加多项式的阶数又会产生不稳定的结果[3]。Hastie 等提出了广义可加模型[4]112-113;Wood在广义可加模型中考虑了连续变量的平滑效应,使模型的拟合效果更加符合实际[5]45-78。对于分层数据的处理,Ruppert 等探讨了广义可加混合效应模型的应用[6]67-86[7];Brezger 等应用MCMC方法估计该类模型的参数[8-10];Silva 等应用贝叶斯混合效应B样条来分析健康指标在各地区间的非线性变化[11];Rigby 等提出了基于位置、尺度和形状参数的广义可加模型(GAMLSS)[12],该模型可以进一步扩展为对因变量的多个参数通过连接函数建立解释变量的可加模型,并在回归方程中包含解释变量的线性效应、连续变量的非线性平滑效应等[13]223-226。
为了探索非线性混合模型在非寿险精算中的应用,分析一组具有非线性关系的保险损失数据,尝试应用一般多项式、截断多项式和B样条三种非线性表达式建立非线性混合效应模型,这些非线性形式在上面的文献中都有涉及。但是,根据响应变量的分布特征,本文进一步探讨因变量服从混合分布条件下的建模问题,并对混合分布中的每一个分布进行非线性回归分析。通过对各种模型的比较分析,可以发现非线性混合效应模型可以有效改善对保险损失的预测效果。
二、非线性混合效应模型
线性混合效应模型假设均值参数的回归方程中含有线性可加的解释变量[14]254-256,虽然线性混合效应模型的适用范围较为广泛,但是变量之间的非线性关系也比较常见。最简单的非线性形式是多项式,该形式能够给出数据整体性的趋势变化,但是缺乏对局部异常波动的拟合能力。在一些实际应用中,非线性表达式的形式是未知的,需要通过数据进行估计,这种非线性关系称为非参数形式。在回归模型中,如果只有部分变量具有非线性效应,这就生成了半参回归模型[15]。Wu 等讨论了如何应用似然方法处理非参数混合效应模型[16]341-342,本文将主要应用贝叶斯方法建立非线性混合效应模型。
假设观察数据中共有m个不同的观察对象,每个观察对象具有n个观察值{yij,i=1,2,…,m,j=1,2,…,n},每个观察值服从下述的指数分布族:
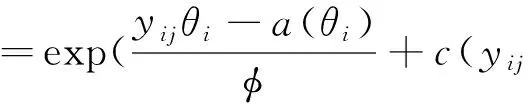
(1)
上述分布的均值为E(yij)=μij=a′(θi),均值的回归方程为g(μij)=ηij,其中g(·) 为连接函数。
假设数据中有K个解释变量(xij1,xij2,…,xijK),应用非参数的方式进行建模,则均值回归方程可以表示为:
g(μij)=ηij=Xijα+Zijβi+S1(xij1)+…+SK(xijK)
(2)
其中Xij和Zij表示解释变量向量,参数α和βi分别表示固定效应和随机效应,回归方程的前半部分Xijα+Zijβi为线性方程,后半部分为解释变量的平滑函数S(xijk)。本文主要研究的平滑函数为多项式、截断多项式和B样条。
(一)多项式模型
多项式非线性模型比较简单,假设某解释变量xijk的平滑函数S(xijk)为多项式,即S(xijk)=γi0+γi1xijk+…+γilxijkl,这是一个l阶多项式,其中回归参数γ是随机效应参数,也可以定义成固定效应参数。多项式回归方程对于波动趋势不显著的曲线拟合效果较好,但是对于比较复杂的曲线关系,需要在变量xijk的定义区间内选取不同的节点。
(二)截断多项式模型


(3)

(三)B样条多项式模型
l阶的B样条多项式有r个节点,可以表示成r+l+1=K个基函数的线性组合。变量xijk的B样条平滑函数S(xijk)可以表示为:

(4)
其中B样条基函数的定义如下:

(5)
当l=1时的基函数为:

(6)
每一个基函数由区间[κj-1,κj)和[κj,κj+1)上的两个线性部分组成,在节点κj处连接。
更高阶的B样条基函数可以通过下面的递推公式求得:

(7)
(四)惩罚样条(P样条)
在截断多项式回归模型中,最小化下述的惩罚残差平方和可以避免出现较大的参数估计值以及过拟合现象:
(8)
平滑系数λ≥0用于控制惩罚项的影响。当λ→0时,惩罚项的影响消失,得到参数γ的最小二乘估计值;当λ→时,参数估计值为,平滑函数f(yij)即为l阶多项式。
三、贝叶斯非线性混合效应模型的参数估计与模型评价
(一)贝叶斯非线性混合效应模型的参数估计
非线性回归模型的参数估计比较复杂,对于上面介绍的惩罚样条模型除了可以应用惩罚最小二乘方法进行估计外,也可以应用贝叶斯方法对惩罚样条参数进行估计。下面主要对惩罚样条多项式回归模型进行分析。
在贝叶斯方法中,无需单独列出惩罚项,而是给出样条参数γ的先验分布,应用随机游走的动态表达式表示差异性惩罚项,一阶随机游走可以表示为:
γj=γj-1+uj,uj~N(0,τ2),j=2,3,…,K
(9)
对于上面的一阶差分需要给出起点值γ1的先验分布,如果没有任何信息,可以假设γ1的先验分布为p(γ1)∝const,其中const表示任意常数值。其他样条参数的先验分布以条件分布的形式出现:
γj|γj-1,…,γ1~N(γj-1,τ2)
(10)
参数γj的期望值为其滞后值γj-1,误差项uj的方差为τ2,该方差值越大,说明实际值对期望均值的偏离越大。

(11)
可见,该联合分布是多元正态分布。对于更高阶的随机游走过程,可以得出相似的结果。参数γ二阶随机游走先验分布定义为:
γj=2γj-1-γj-2+uj,uj~N(0,τ2) j=3,4,…,K
(12)
无信息初始参数的先验分布为p(γ1)∝const和p(γ2)∝const。根据二阶随机游走的假设,条件分布为:
γj|γj-1,γj-2,…,γ1~N(2γj-1-γj-2,τ2)
(13)
应用贝叶斯方法估计模型参数还需要给出其他未知参数的先验分布,比如方差参数可以选用逆伽玛分布,模型中的一般回归参数可以选用均值为零的正态分布等。假设模型中各参数的先验分布相互独立,可以得出模型各参数的联合后验分布,通过该后验分布可以得出模型参数的估计值及估计区间。本文应用蒙特卡罗方法中的Gibbs抽样,通过模型参数的全条件分布进行重复抽样,得到所估参数的后验分布样本,进而可以得到参数的均值、方差和置信区间等统计量。
(二)贝叶斯非线性混合效应模型的评价
应用Gibbs抽样可以得到模型参数后验分布的一系列样本,这些样本可能存在自相关,因而需要检验样本是否收敛。对于MCMC模拟样本的收敛性检验方法有:模拟样本轨迹图、自相关检验和Gelman-Rubin统计量等[17]。为了得到Gelman-Rubin统计量的估计值,需要同时给出不同初始值生成几个样本链,比较分析样本之间和样本内部的可变性,如果该统计量的结果趋向于1,说明模型参数估计值达到了平稳的收敛状态。
贝叶斯方法可以给出各参数的后验分布,从而求得各个参数的估计值及其信度区间。应用参数估计值的信度区间就可以对参数进行显著性检验,如果该区间内含有零值,说明该参数值是不显著的,具体可参见Kruschke的研究[18]113-117。
一般而言,参数较多的模型对观察数据的拟合较好,但其预测能力较差。在比较和选择不同的模型时,通常使用AIC或BIC统计量,它们都含有一个惩罚项来抵消由于参数增加而增加的模型拟合效果。对于固定效应模型,模型的参数个数比较容易确定;对于混合效应模型,模型的有效参数个数并不明确。如果随机效应的方差较大,该随机效应参数就比较显著;反之,如果随机效应的方差较小,随机效应参数在模型中的作用就比较小。由于混合效应模型含有随机效应参数,所以本文应用贝叶斯模型常用的检验标准DIC(Deviance information criterion)统计量来对不同模型进行比较和评价,它能够估计贝叶斯混合效应模型的“有效”参数个数[19-20]。DIC统计量表达形式如下所示:

(14)

四、案例分析
欧洲交通安全理事会每年统计并发布欧洲31个国家的交通事故伤亡人数数据*参见Ranking EU Progress on Road Safety-8th Road Safety Performance Index Report, http://etsc.eu/ 2014(6)。。本文选用死亡人数数据进行建模分析。由于不同国家的人口数量不同,各国交通死亡人数差别较大,为了便于比较,本文选用百万人口交通事故死亡率(以下简称死亡人数)进行分析。各国死亡人数的观察期为2001年至2013年,图1和图2分别给出了欧洲31个国家13年内交通事故死亡人数分布和各年死亡人数趋势。
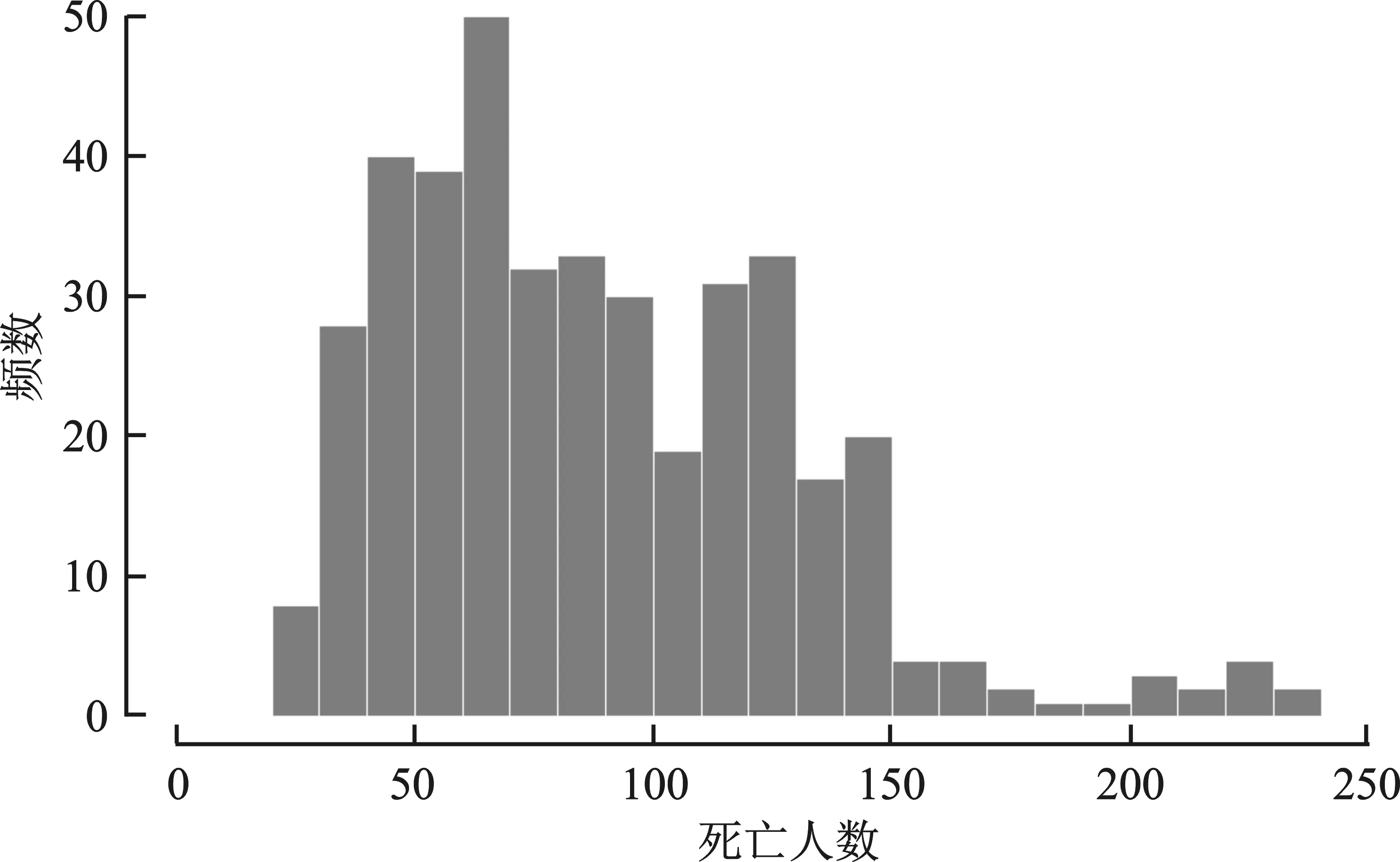
图1 交通事故死亡人数分布图
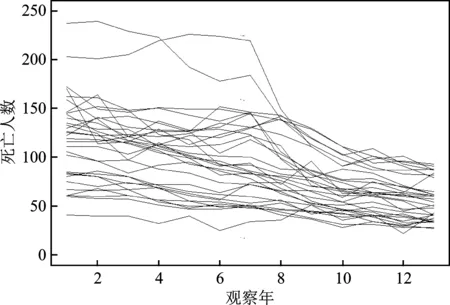
图2 交通事故死亡人数趋势图
从分布图可以看出,死亡人数是多峰结构,且在观察期限内具有非线性变化趋势。下面以死亡人数为响应变量建立回归模型,可以选择的解释变量有人均GDP和观察年度。在建模过程中发现人均GDP的作用并不明显,所以只考虑年度作为解释变量。
假设死亡人数yij服从泊松分布,解释变量各观察年表示为xij,两个下标i=1,2,…,31和j=1,2,…,13分别表示31个国家和13个观察年。
基于本文的数据,可以建立下述10个模型进行比较分析。
模型一:假设死亡人数服从泊松分布,对均值参数建立具有对数连接函数的线性混合效应模型:
yij~Poisson(μij)
log(μij)=γi1+γi2xij
模型二:假设死亡人数服从混合泊松分布,其均值参数的回归方程为线性混合效应模型:
log(μijk)=γik1+γik2xij
模型三:图2表明死亡人数随各年度呈现出非线性变化趋势,所以考虑建立多项式混合效应模型:
yij~Poisson(μij)
模型四:在模型三的基础上假设死亡人数服从混合泊松分布,同时对不同的均值参数建立回归方程:
模型五:图2 显示出死亡人数随年度呈现出递减的变化趋势,且各条曲线波动明显,考虑在均值参数的回归方程中加入截断多项式,假设截断多项式参数为随机效应参数,其他参数为固定效应参数,其中κ1,κ2,…,κm表示节点。
yij~Poisson(μij)
模型六:在模型五的基础上假设死亡人数服从混合泊松分布:
模型七:在模型五的基础上假设回归方程中所有参数为随机效应参数:
yij~Poisson(μij)
模型八:在模型七的基础上假设死亡人数服从混合泊松分布:
模型九:针对死亡人数随年度呈现出递减的变化趋势,考虑在均值参数的回归方程中加入B样条,模型中B样条参数为随机效应参数,其他参数为固定效应参数:
yij~Poisson(μij)
模型十:在模型九的基础上,假设死亡人数服从混合泊松分布:
以上10个模型可以分为四类,模型一和模型二是线性混合效应模型;模型三和模型四是多项式混合效应模型;模型五、六、七、八是截断多项式混合效应模型;模型九、十可以称为B样条混合效应模型。
由于这些模型比较复杂,本文使用贝叶斯方法对模型进行估计。在上述模型中,假设混合效应参数(γi1,γi2)的先验分布为均值为零的二元正态分布,即(γi1,γi2)~N2(0,Σ),其中Σ为超参数,其先验分布为自由度为2的逆沙维特分布(Inv-Wishart),即Σ~Inv-Wishart2(I),I表示二维的单位矩阵。模型三和模型四的混合效应参数服从三元正态分布。
当死亡人数服从混合泊松分布时,模型中含有比例参数p,该参数在(0,1)区间内取值,将其定义为pk=eλk/(eλ1+eλ2+…+eλC),其中λ1=0,当k>1时λk~N(0,1)。经过模型比较发现,当两个泊松分布进行混合时,模型的拟合效果较好,所以在本文中C=2。
在上述模型中分别采用了1阶截断多项式和3阶B样条,并对13个观察年度进行了中心化处理。选取的5个节点分别是-4、-2、0、2、4,所以在截断多项式模型中m=5,即含有5个截断项,在B样条模型中K=9。

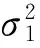
根据表1给出部分参数的估计值和模型拟合统计量,可以对上述模型进行比较分析。在模型三和模型四中,参数γ服从三元正态分布,表1只给出了部分结果,在其他模型中,该参数服从二元正态分布。每个混合效应参数γ有31个估计值,表1中只给出它的协方差矩阵Σ。在表1中给出参数估计值的标准误,进而得出估计值的信度区间,通过信度区间确定估计值的统计显著性,比如大部分参数γ的协方差在其95%的信度区间内含有零值,这说明参数γ之间近似相互独立。参数p给出了两个泊松分布的混合比例。Deviance(负二倍的对数似然函数)和DIC统计量用于模型比较,这两个统计量的值越小表示模型越好。可以看出,混合泊松分布模型的Deviance统计量小于同类模型,但是DIC统计量相对较大。这说明虽然混合泊松分布模型的拟合效果较好,但是涉及参数较多,优势并不明显。从上述十个模型的拟合效果来看,非线性模型的拟合效果优于线性模型,样条多项式优于一般多项式,B样条优于截断样条。总体来看,模型九的Deviance统计量为2 791.28,DIC统计量为2 911,在上述所有模型中是最小的,所以是相对最优的模型。另外模型九涉及参数相对较少,便于操作,更具有实际应用价值。

表1 参数估计结果
注:括号中的数字为估计值的标准误。
五、结 论
由于实际的保险损失纵向数据中,变量之间关系比较复杂,变量间的非线性关系更具有一般性。很多研究为了分析的简便,假设变量之间存在简单的线性关系,这并不适合具体的实际应用。本文基于一组实际保险损失数据建立了截断多项式混合效应模型和B样条混合效应模型,并与一般的线性混合效应模型进行了比较,结果表明,非线性混合效应模型能够更好地拟合该组实际数据。在非寿险损失预测和费率厘定实践中,解释变量与响应变量之间往往存在非线性变化关系,甚至存在波动性的趋势变化,在这种情况下应该考虑建立非线性混合效应模型。非线性混合效应模型是对一般线性混合效应模型的扩展,能够更好地满足实际应用中对复杂保险损失数据建模的需要,对非寿险费率厘定具有重要价值。
[1] 孟生旺,邱子真. 混合效应模型及其在非寿险费率厘定中的应用[J]. 数理统计与管理, 2016(1).
[2] 王明高,孟生旺. 基于贝叶斯偏态线性混合模型的费率厘定[J]. 统计与信息论坛,2015(1).
[3] Klein N, Denuit M. Stefan Lang, Thomas Kneib. Nonlife Ratemaking and Risk Management with Bayesian Generalized Additive Models for Location, Scale, and Shape[J].Insurance: Mathematics and Economics, 2014(5).
[4] Hastie T, Tibshirani R. Generalized Additive Models[M]. London: Chapman and Hall, 1990.
[5] Wood S N. Generalized Additive Models: An Introduction with R[M]. London: Chapmann & Hall, 2006.
[6] Ruppert D, Wand M P, Carroll R J. Semiparametric Regression[M]. Combridge: Cambridge University Press,2003.
[7] Wood S N. Fast Stable Direct Fitting and Smoothnesss Election for Generalized Additive Models[J]. Journal of the Royal Statistical Society (B), 2008(4).
[8] Brezger A, Lang S. Generalized Structured Additive Regression Based on Bayesian P-splines[J]. Computational Statistics & Data Analysis, 2006(3).
[9] Jullion A, Lambert P. RobustSpecification of the Roughness Penalty Prior Distribution in Spatially Adaptive Bayesian P-splines Models[J]. Computational Statistics & Data Analysis, 2007(2).
[10]Lang S, Umlauf N, Wechselberger P, et al. Multilevel Structured Additive Regression[J]. Statistics and Computing, 2014(6).
[11]Silva G, Dean C, Niyonsenga T, Vanasse A. Hierarchical Bayesian Spatiotemporal Analysis of Revascularization Odds Using Smoothing Splines[J]. Statistics in Medicine, 2008(2).
[12]Rigby R A, Stasinopoulos D M. Generalized Additive Models for Location, Scale and Shape (with Discussion)[J]. Applied Statistics, 2005(3).
[13]Fahrmeir L, Kneib T, Lang S, Marx B. Regression-Models, Methods and Applications[M]. New York:Springer, 2013.
[14]Goldstein H. Multilevel Statistical Models[M]. 4rd ed. Chichester: John Wiley, 2011.
[15]Beck N, Jackman S. Beyond Linearity by Default: Generalized Additive Models[J]. American Journal of Political Science, 1998(5).
[16]Wu H, Zhang J T. Nonparametric Regression Methods for Longitudinal Data Analysis[M]. Chichester: John Wiley, 2006.
[17]Gelman A,Rubin D. Inference from Iterative Simulation Using Multiple Sequences[J]. Statistical Science, 1992(7).
[18]Kruschke J K. Doing Bayesian Data Analysis[M].London: Academic Press, 2011.
[19]Spiegelhalter D J, Best N G, Carlin B P, Van Der Linde A. Bayesian Measures of Model Complexity and Fit (with Discussion) [J]. Journal of the Royal Statistical Society(B), 2002(2).
[20]Spiegelhalter D J, Best N G, Carlin B P, et al. The Deviance Information Criterion: 12 Years on [J]. Journal of the Royal Statistical Society(B), 2014(1).
(责任编辑:崔国平)
Bayesian Nonlinear Mixed Effects Models and Their Applications
WANG Ming-gao1,2,MENG Sheng-wang2
(1. School of Statistics, Shandong Institute of Business and Technology, Yantai 264005, China;2. Center for Applied Statistics, Renmin University of China, Beijing 100872, China)
Linear mixed effects models have some limitations to model longitudinal data with nonlinear relationship. The paper extends the linear mixed effects models, and based on the nonlinear relationship of variables and the distribution of dependent variable, different nonlinear mixed-effects regression models are established. Using a set of insurance loss data, the paper establishes polynomial mixed effects models, truncated polynomial mixed effects models and B-spline mixed effects models. The result shows that the nonlinear moixed effects models can significantly improve the prediction of the insurance loss. Models established in this paper extends the application of mixed-effects model, and has important value for non-life insurance ratemaking.
mixed effects models; nonlinear models; insured loss; Bayesian
2016-03-25
国家自然科学基金项目《考虑风险相依的非寿险精算模型研究》(71171193);山东省社会科学基金项目《基于贝叶斯分层MCMC对山东保险市场区域差异及协同发展对策性研究》(15CTJJ01);山东工商学院博士科研基金项目《贝叶斯分层模型的应用研究》(BS201508)
王明高,男,山东日照人,经济学博士,讲师,研究方向: 风险管理与精算; 孟生旺,男,甘肃秦安人,经济学博士,教授,博士生导师,研究方向: 风险管理与精算,应用统计。
O212∶F840.3
A
1007-3116(2016)12-0010-07
