拼装误差对箱型截面拱桥拱圈强度的影响分析

李自林，史旭东，石迎新

（1.天津城建大学，天津 300384；2.中铁十八局集团第二工程有限公司，河北 唐山 063000）

拼装误差对箱型截面拱桥拱圈强度的影响分析

李自林1，史旭东1，石迎新2

（1.天津城建大学，天津 300384；2.中铁十八局集团第二工程有限公司，河北 唐山 063000）

以成贵铁路西溪河大桥为工程背景，利用ANSYS11.0模拟分析拱圈拼装过程中产生的纵向偏差误差及截面偏差角对拱圈强度的影响.结果表明：纵向偏差及截面偏差角均会影响桥梁拱圈的强度；桥梁拱圈内的应力值随纵向偏差及截面偏差角的增大而增大；截面偏差角对桥梁拱圈强度的影响要大于纵向偏差对桥梁拱圈强度的影响.

箱型截面；拼装误差；组合误差；拱圈强度

大跨度拱桥是公路和铁路跨越峡谷、江河和山区深沟的主要桥梁结构形式之一.尤其是钢管混凝土拱桥，其结构轻巧，造型美观，承载能力、跨越能力和地基适应能力强，在现代桥梁建设中得到了广泛的应用［1］.拱圈作为桥梁主体的一部分，对其进行强度分析具有重要的意义.既有拱桥在荷载、基础变位和环境条件等因素的长期作用下，拱圈（拱肋）的轴线不可避免地要发生变化，而拱轴线型形状的改变又直接影响拱圈内力及截面应力的分布［2-3］.拱圈拼装过程中采用支架固定拱圈，利用全站仪测定拱圈线形［4-5］.由于工人操作、环境影响和拱圈自重等因素的影响，拱圈线形难免会产生拼装误差，使拱圈实际线形与设计要求的线形有偏差，从而影响拱圈强度［6］.箱型截面较哑铃形截面抗弯刚度大，造型美观，但由于其截面较为复杂，使得拱圈线形偏差对拱圈强度的影响更为严重［7-9］.本文对拼装误差引起的箱型截面拱桥拱圈强度变化进行研究.

1 工程概况

本工程为成贵铁路西溪河大桥，跨越深切河谷西溪河，全长493.6，m.拱圈由两条拱肋与横向连接系构成，拱趾中心跨度为240，m，拱肋横向内倾7.5°，拱趾处中心距为23.192，m，拱顶两肋中心距为8.71，m.拱轴系数m=2.2，矢跨比约1/4.364.拱肋高5.7，m，宽3.0，m.每肋由4支Φ1，100，mm× 20，mm钢管构成，上弦之间和下弦之间均由两块20，mm厚的钢板联结成空心哑铃型，在拱肋的全长上均为等截面；上下弦之间各由两块16，mm厚的钢板联结，构成实腹段，使拱肋截面呈箱型.

2 拱肋吊装及合龙

2.1 钢管拱制造和运输

钢管拱由专业厂家制造.在工厂将钢管拱肋上、下弦用3～8，m节段钢管加工制造成哑铃型，并进行1/4预拼.各节段预拼装时，应在各接口处做出相应标志.经检查合格后，分段起吊.拱肋通过火车及汽车运至钢管拱存放现场，利用汽车吊将钢管拱按一定顺序起吊存放，并支垫牢靠.

2.2 钢管拱拱肋组拼

在支架上按设计线型位置将拱肋下弦2～3节段对接拼装并固定，然后在其上搭设支架，架设2～3节上弦哑钤型肋段，并将上弦拱肋调整至设计线型，各肋段接头点焊.再将上、下弦拱肋的连接腹板安装上并施焊（自内向外焊接），施焊同时逐步拆除上弦拱肋的支点.按上述步骤从拱肋的拱脚向拱顶，依次由下向上、由内向外，分别安装两实腹段拱肋.与此同时，务必在每一节段完成时，调整一次拱肋的线型.

2.3 钢管拱转体及合龙

在钢管拱拱肋及交界墩拼装施工完毕，并检查合格后，选择在微风或无风气候下，对称张拉交界墩后背索、钢管拱拱肋前扣索和最后一批上转盘的纵向预应力钢束，使钢管拱形成转体状态.在钢管拱肋脱离支架后，通过加载、配重等方法，使其形成以球铰为中心的平衡转体体系.待转体体系检查合格后，将其静置48，h，测量、观察转体体系是否有异常现象，同时通过预埋装置检查半跨钢管拱肋受力是否正常.

在施工两岸各安装一套同步的全自动、全液压、连续牵引的系统.经两套系统试调完成后，将由上转盘转台引出的钢绞线穿入牵引千斤顶.先手动起动转体系统试转，由于起动时转体间的静摩擦系数太大，故需要用辅助千斤顶来帮助主作用千斤顶启动牵引.在手动试转正常后，将辅助千斤顶退出转体工作，主千斤顶即可切换至“自动”运行状态.为防止半跨钢管拱转体超转，转体快到设计位置时，将牵引系统切换至手动、点动操作，以保证拱体精确定位.转体到位后，对两端拱肋进行微调和锁定，最后再进行合龙段的施工.

3 拼装误差对拱圈强度的影响

3.1 拱圈拼装误差原因

拱圈在出厂拼装过程中，虽对拼装的1/4拱圈进行检查，但并不能保证拱圈不产生微小变形或拱圈轴线与设计轴线相一致；拱圈在现场拼装过程中，容易因为现场施工环境、工人操作及其他相关因素影响，致使拱圈实际拱轴线与设计轴线不符；在拱圈进行转体合龙过程中，底座转体不平稳、基础轴线微小偏差、支座轴线微小偏差等因素均会导致拱圈实际轴线与设计轴线不符.

3.2 拱圈拼装误差形式

实际施工过程中，为使合龙时两端轴线符合设计要求，会在合龙端施加一定的力或扭矩，使轴线调整符合设计要求，这就使得拱圈在拼装合龙完成后拱圈内具有一定的初始应力，从而影响拱圈的强度.

本工程拱圈采用转体合龙方式完成拼装，截面横向拼装误差为可调整误差；但拱圈截面纵向及偏差角度均为不易调整误差.故针对拱圈截面纵向误差（如图1），采取施加纵向力，使截面轴线纵向对齐；针对拱圈截面角度误差（如图2），采取施加截面扭转力，使截面轴线对齐；针对同时具有纵向误差及截面偏差角误差的情形（如图3），采取同时施加纵向力及扭矩的方式进行纠偏.

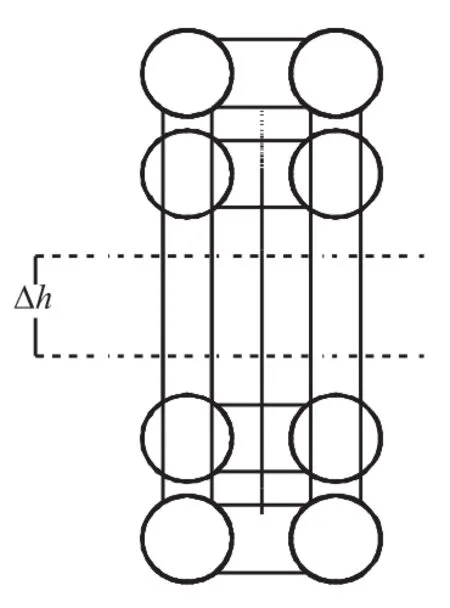
图1 纵向误差

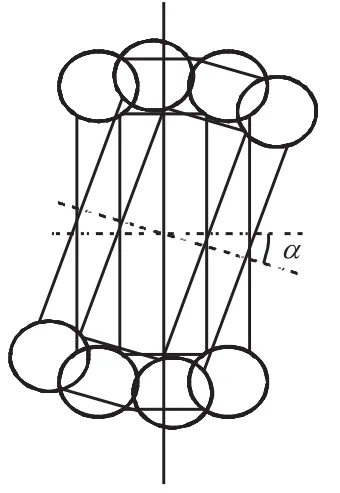
图2 截面偏差角

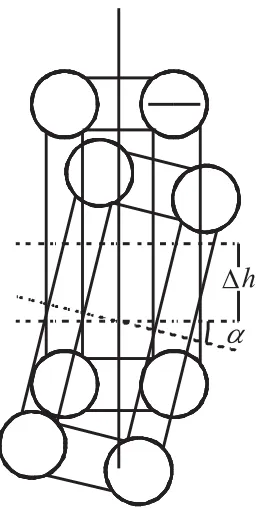
图3 纵向误差+截面偏差角

3.3 拱圈结构模型

桥梁拱圈由双哑铃型截面焊接成箱型截面，每段拱肋由3～8，m钢管焊接而成.结构简化模型如图4所示.

图4 结构简化模型

3.4 拱圈有限元模型

本文采用有限元程序ansys11.0为工具进行模拟分析.桥梁拱圈由Q345钢材制成，材料为理想弹塑形模型，弹性模量E=2.06×106，MPa，泊松比μ= 0.28，钢材屈服强度σy=345，MPa，密度为7，850 kg/m3，考虑到结构的对称性及截面的均匀性，建模时先建模型截面，用截面按桥轴线直接拉伸出拱圈模型.为方便分析，采用soild45单元建模.进行网络划分时，先对整体进行智能网络划分，再对局部进行细化划分.

在实际施工过程中，施工误差值一般不会太大，故本文在进行有限元模型模拟误差计算时，采用微小误差值进行模拟分析，所采用的误差值及形式如表1所示.

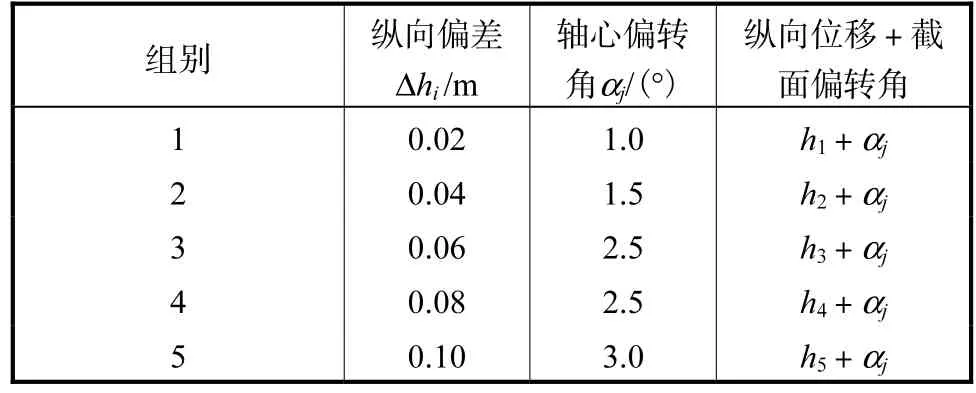
表1 误差表

进行有限元模拟分析时，先对半拱圈进行误差分析，再将得到的半拱圈内力加到拱圈整体中进行模拟分析，得到由误差引起的拱圈内应力情况.计算结果如表2-4所示.

表2 纵向偏差引起的应力值

表3 截面偏差角引起的应力值

表4 组合偏差引起的应力值 MPa

4 拼装误差对拱圈强度的影响

由计算结果绘制出应力值变化图，如图5-7所示.

由图5-7，对本桥梁拱圈进行分析，可以得到如下结果.

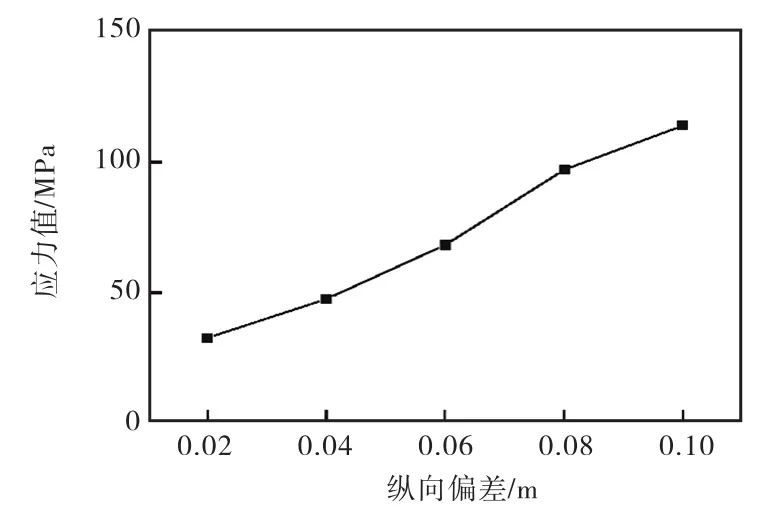
图5 纵向偏差引起的应力值变化

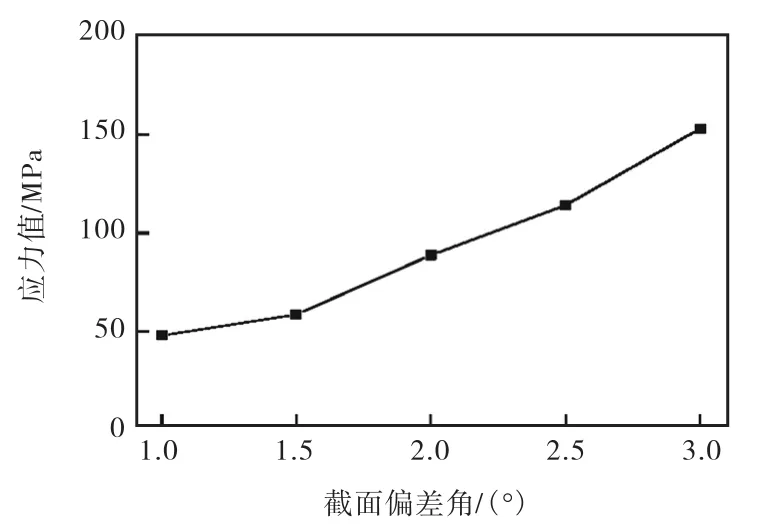
图6 截面偏差角引起的应力值变化

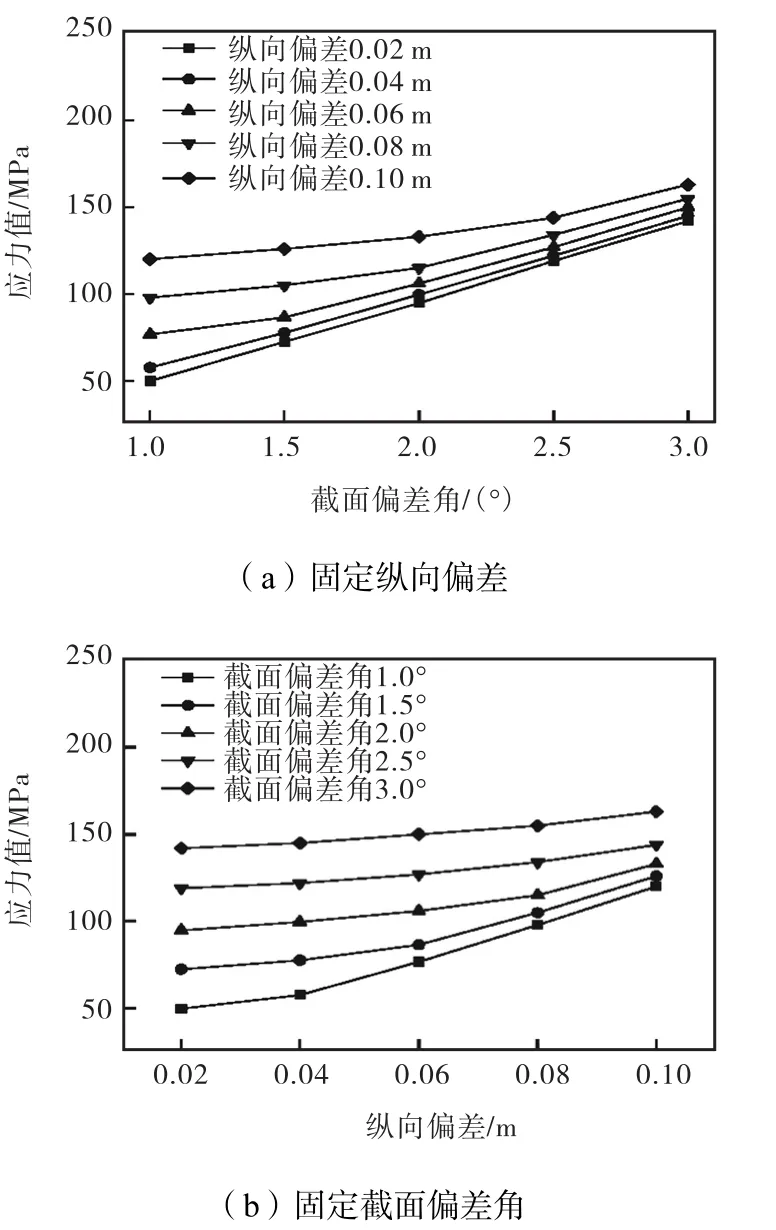
图7 组合误差引起的应力值变化

（1）由拼装引起的施工误差在一定范围内不会引起拱圈结构的破坏，但会降低拱圈的强度，从而对桥梁整体的强度产生影响；由拼装误差引起的拱圈内应力值随拼装纵向偏差值的增大而增大，且其应力值曲线斜率随纵向偏差值的增大而增大，即由拱圈纵向偏差引起的拱圈内应力值增长率逐渐增大，超过一定数值必将造成拱圈结构的破坏；由拼装误差引起的拱圈内应力值随拼装截面偏差角的增大而增大，且其应力值曲线斜率随纵向偏差值的增大而增大，即由拱圈截面偏差角引起的拱圈内应力值增长率逐渐增大，转角偏差过大，必将造成拱圈结构的破坏.

（2）对同时具有纵向偏差及截面偏差角的拱圈，拱圈内应力值随组合误差值的增大而增大.但拱圈内应力值的增长率随组合误差数值的增大而减小，原因是由组合误差引起的受力十分复杂，与简单受力情况下的应力值增长率并不相同.

（3）桥梁拱圈在同时具有纵向偏差及截面偏差角的情况下，在任一截面上，拱圈内应力值最大处在截面垂直于拱圈轴线的纵向上，如图8（纵向偏差0.10，m，截面偏差角3.0°时拱趾处）所示.

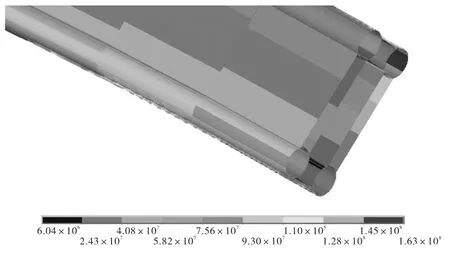
图8 拱趾应力云图

（4）桥梁拱圈在组合误差的情况下，拱圈内应力分布并不均匀，因为拱圈两端受到的力并非对称力.但任一组合误差情况下，拱圈内应力值最大点均位于跨中位置，如图9所示.

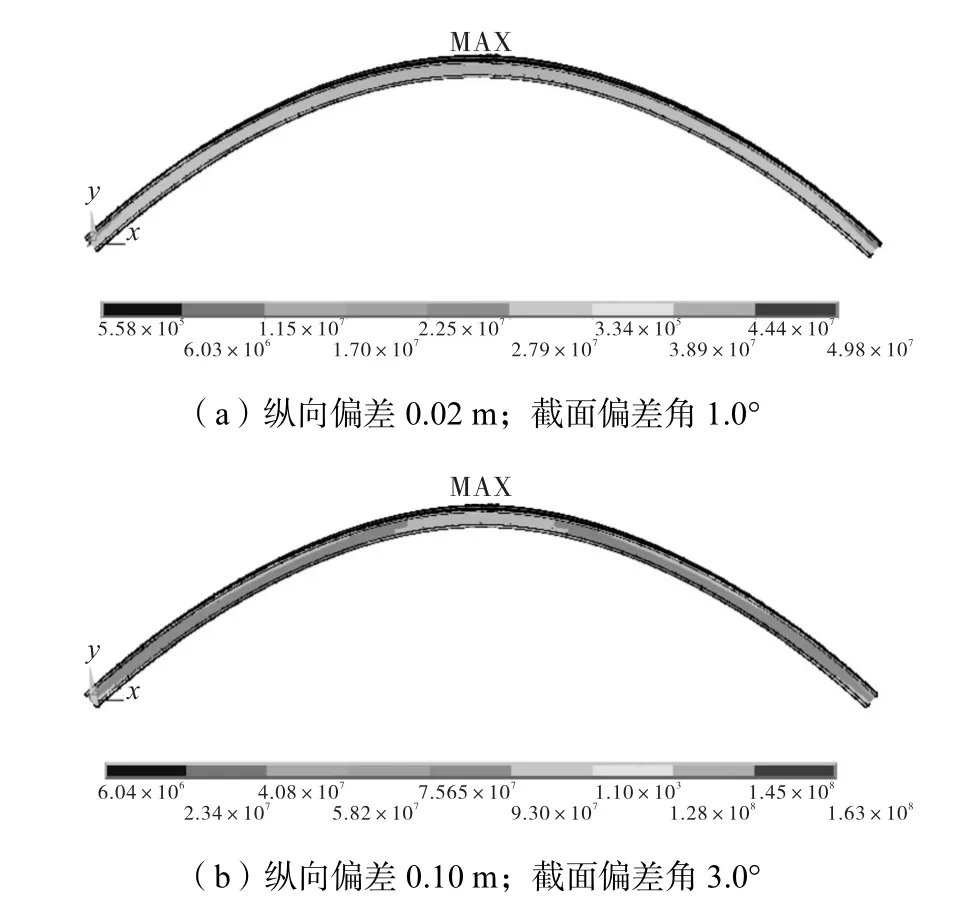
图9 组合误差下拱圈内应力云图

（5）由组合误差引起的应力值在既定纵向偏差数值的情况下，其增长速率随截面偏差角的增大而增大；由组合误差引起的应力值在既定截面偏差角数值的情况下，其增长速率随纵向偏差数值的增大而减小；由组合误差引起的应力值变化曲线可以看出，截面偏转角误差对桥梁拱圈内应力值的影响要大于纵向偏差对桥梁拱圈内应力值的影响.

5 结 论

在实际施工工程中，拱圈拼装误差普遍存在，其对拱圈强度的影响十分明显.本文着重研究了拱圈拼装过程中产生的纵向偏差及截面偏差角对拱圈强度的影响，得到如下结论：

（1）拱圈拼装误差在一定范围内时并不会导致桥梁拱圈的破坏，但会影响桥梁拱圈的强度，从而对桥梁整体造成影响.

（2）拱圈拼装误差引起的拱圈内应力值随误差的类型、大小的变化而变化，拱圈内应力值随各种误差数值的增大而增大.单种误差所引起的拱圈内应力值要比多种误差同时存在情况下拱圈内应力值小，在实际施工过程中，应尽量控制桥梁线形，使之仅有一种误差.

（3）在同时具有纵向误差及截面偏差角的情况下，截面偏差角对桥梁拱圈强度的影响要大于纵向偏差误差对桥梁拱圈强度的影响.在实际施工过程中，应尽量避免截面偏差角.

（4）在纵向误差及截面偏差角均较大时，由拼装误差引起的应力高达150～163，MPa，达到钢材屈服强度的40%，以上，考虑后期叠加正常使用阶段的应力，对拱桥十分不利.故在实际施工过程中，纵向误差值不应大于0.10，m，截面偏差角不应大于2.5°.

［1］李 艳，赵均海，张常光，等.哑铃型钢管混凝土拱肋极限承载力研究 ［J］.计算力学学报，2015，32（2）：99-106.

［2］温庆杰，叶见曙.缺失技术资料的旧拱桥现场调查方法研究［J］.公路交通科技，2006，23（4）：62-65.

［3］钟正强，罗纪彬，彭振斌.拱轴线形激光断面仪的测试方法［J］.中外公路，2009，29（3）：126-128.

［4］陈顺超，黄平明，孙胜江.免棱镜全站仪测量拱圈线性及其精度分析［J］.工程勘察，2011，7：66-69.

［5］陈顺超，黄平明，孙胜江.测定既有拱桥拱圈线性的改进悬高测量法［J］.测绘通报，2012，1：50-52.

［6］刘 剑.大跨径钢管混凝土劲性骨架拱桥主拱圈施工方案研究［D］.西安：长安大学，2007.

［7］陈定波.大跨度刚箱梁斜拉桥施工控制中的误差分析［D］.成都：西南交通大学，2008.

［8］桂许兰.公路桥梁施工状态误差分析及其标准研究［D］.重庆：重庆交通大学，2014.

［9］周 嫚.悬臂拼装曲线连续桥梁施工误差敏感性分析［D］.重庆：重庆交通大学，2012.

Analysis of the Influence of Assembly Errors on the Box Section Arch Strength of Arch Bridge

LI Zilin1，SHI Xudong1，SHI Yingxin2
（1.Tianjin Chengjian University，Tianjin 300384，China；2.The 2th Engineering Co.，Ltd of the 18th China Railway Construction Bureau，Tangshan 063000，Hebei，China）

With the Xixi River Bridge on the route of Chengdu-Guiyang Railway as engineering background，this paper uses ANSYS11.0 to analyze the influence of longitudinal error and cross section deviation angle on the strength of the arch.The research result shows that：①longitudinal error and cross section deviation angle will influence the strength of bridge arch；②the bridge arch stress value increases as longitudinal error and cross section deviation angle increase；③the influence of cross section deviation angle on the strength of the bridge arch is greater than that of longitudinal deviation.

box section；assembly error；combined error；arch strength

U448.22

A

2095-719X（2016）04-0273-05

2015-06-23；

2015-07-07

住建部科学技术项目（2015-K3-021）；天津市自然科学基金项目（13JCYBJC19600）；天津市交通运输委员会科技项目（2014-23）

李自林（1953—），男，河北成安人，天津城建大学教授.