经济新常态下农产品价格波动趋势分析

罗光强，周 黎

（湖南农业大学 经济学院，长沙 410128）

经济新常态下农产品价格波动趋势分析

罗光强，周 黎

（湖南农业大学 经济学院，长沙 410128）

文章利用2008年1月至2015年9月的全国农产品批发价格总指数数据，选择ARMA模型，预测2015年10月至2020年12月的全国农产品批发价格总指数；并以此为基础，运用季节分析法与滤波法分析农产品价格波动的趋势与特征。结果表明：经济新常态下农产品价格波动整体呈现周期性上升态势，农产品价格波动的季节性和周期性特征明显。因此，促进我国农产品市场稳定运行需要谨防季节性和跨周期性的内外冲击。

经济新常态；农产品市场；波动特征

0 引言

农产品价格波动既是一个历史事实，又是一个客观现象；这种现象不论是哪个区域或哪个国家，只要是市场经济环境下总是客观存在的，即使进行市场干预其波动现象仍然是不可避免的。综观世界各国农产品市场，其波动表现总体呈现出周期性、季节性和非常规性等不同形式。因此，掌控农产品市场价格波动规律，防范农产品市场价格异常波动固然成为世界各国宏观调控、中观规制和微观干预的重要指向和指标。引致农产品市场价格波动的因素很多，总体来说，这些因素普遍具有共性特征，只是在各国市场经济的不同阶段和不同环境表现出程度上、时间上、空间上的不同差异。中国正处于一个现代市场经济变革的新时期，亦即经济新常态时期，农产品市场价格波动与我国当期和未期的制度变革、结构转型、产业升级、技术进步等高度相关、密不可分。事实上，中国自改革开放以来，农产品市场价格波动表现频繁，异常波动不断，具有中国经济特征。农产品市场是一个民生市场，农产品价格波动是农产品市场运行的基本特征，规避和防止农产品市场异常波动既是民生福祉基本保障的需要，又是一国经济持续稳定发展的需要。因此，预测经济新常态下我国农产品市场价格波动趋势，分析农产品市场波动的新特征，有利于把握新常态下农产品市场波动规律，促进农产品市场的有效运行。

1 模型选择与数据说明

本文研究的思路是利用既有时间序列数据，预测未来时序表现；因此，本文以下采用时间序列预测模型。考虑到模型的适用性，本文选用ARMA模型。ARMA模型的基本思想是：某些时间序列是依赖于时间t的一组随机变量，构成该时序的单个序列值虽然具有不确定性，但整个序列的变化却有一定的规律性，可以用相应的数学模型近似描述。通过对该数学模型的分析研究，能够更本质地认识时间序列的结构与特征，达到最小方差意义下的最优预测。

首先建立自回归模型AR(p)，p阶自回归模型记作AR (p)，满足下面的方程：

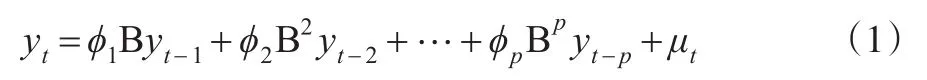
其中ϕ1，ϕ2…，ϕp是自回归模型系数，是模型的待估参数，p为自回归模型阶数；μt是均值为0，方差为σ2的白噪声序列，令模型可简写为

其次建立移动平均模型MA(q)，q阶移动平均模型记作MA(q)，满足下面的方程：

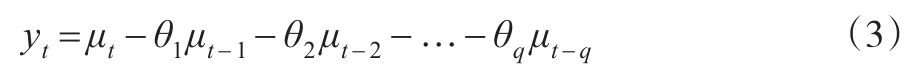
其中：参数θ1、θ2…θq是q阶移动平均模型的系数；μt是均值为0，方差 σ2的白噪声序列，引入滞后算子，MA（q）可简写为 yt=θ（Β）μt，其中 θ（Β）=1-θ1Β-θ2Β2-…-θqΒq。最后将两模型结合有，自回归移动平均模型满足下面的方程：

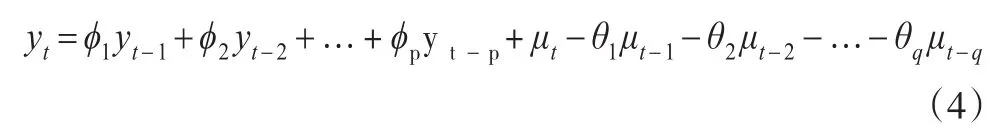
引入滞后算子B，ARMA模型可简记为ϕ（B）yt=θ（B）μt，当然在使用ARMA模型之前应当要检验时间序列的平稳性。

关于本文数据采集基于以下思考。改革开放30多年以来，我国经济基本保持了年均10%左右的增长率，按照经济周期理论，以经济的繁荣、衰退、萧条、复苏为一个经济周期，我们可将2015年前的的经济增长划为四轮周期。第一轮周期是1978—1984年，处于市场经济转型时期，经济增速呈现出V字型走势，呈现出大起大落、忽冷忽热的增长格局。第二轮是1984—1994年，处于市场经济成长时期，经济增速呈现出W型走势，沿袭了上轮周期大起大落、冷热交叉的增长格局。第三轮是1994—2008年，处于市场经济稳定时期，经济增速呈现出宽w字型走势，走出了前两周期大起大落，忽冷忽热的增长格局。第四轮周期从2008年开始至现在，还没有结束。自2008年以来，我国的实际GDP增长率增速开始变缓，经济增长格局也呈现出与往周期增长格局不同，呈现出新的规律，经济增长速度开始放缓，经济结构处于调整转型状态，因而我们可将这种现象定义为新常态时期。基于此，本文选取2008年1月至2015年12月的全国农产品批发价格总指数作为基础数据，并通过该指数趋势图形拟合出与之相似的指数回归曲线，进行ADF检验从而判断是否存在平稳性，最终确定ARMA预测模型。

2 趋势预测

本文以2008—2015年的全国农产品价格（以2000年全国农产品批发价格总指数100为定基）进行我国农产品市场价格的预测分析，数据来源于全国农产品批发市场价格信息网，计量分析软件采用Eviews6.0。首先进行时间序列数据的平稳性检验和处理。全国农产品批发价格总指数时间序列具有明显的递增趋势，近似为一条波动向上的指数函数曲线，是非平稳时间序列，需要对WPI(全国农产品批发价格总指数）进行平稳化处理。将WPI数据进行对数化再取一阶差分后得到DWPI，图1显示出的DWPIA时间序列折线图，可以看出全国农产品批发价格总指数的一阶差分总体上围绕一均值呈现出上下波动状态，较为平稳。

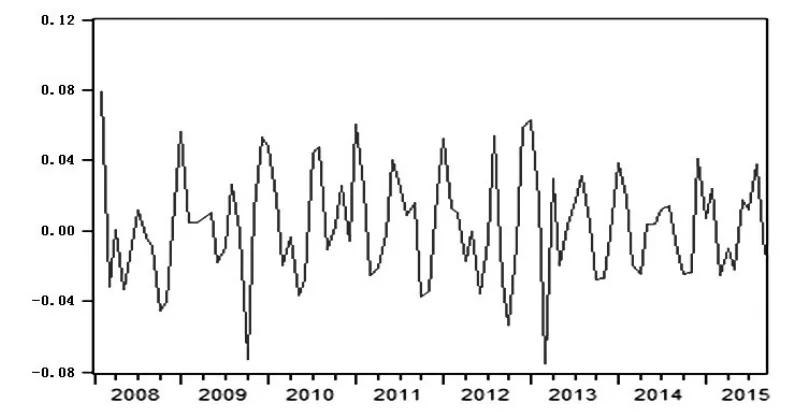
图1 DWPI时间序列折线图

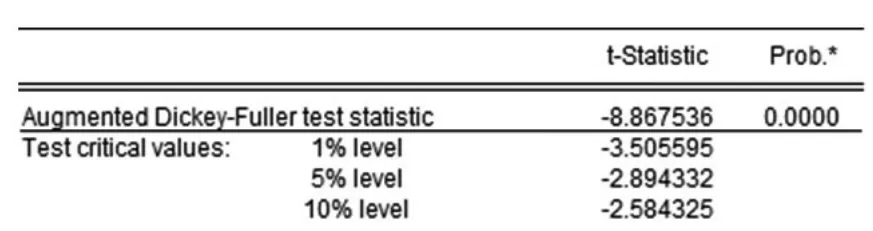
图2 DWPI的ADF检验

对一阶差分序列DWPI进行ADF检验，得到检验结果，如图2所示。由图2中检验结果可知，t统计量为-8.867536，小于检验显著性水平为1%、5%、10%的临界值，而且t统计量对应的概率p值为0.0000，说明时间序列DWPI可以通过ADF检验，即可以认为序列DWPI为平稳序列。我们可以根据DWPI序列建立ARMA模型。

作出DWPI的直到滞后12期的自相关和偏自相关分析图（图3），由图3显示，序列的DWPI的季节性差分SDWPI的自相关与偏自相关系数很快地落入随机区间，但是k=12时取值仍然较大，季节性依然比较明显。对序列进行二阶差分，发现序列季节性并没有得到显著性改善。因而只做一阶季节差分即可。

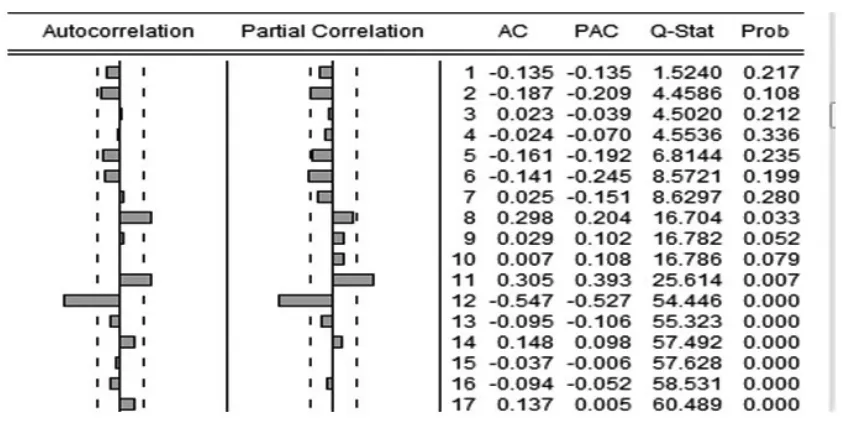
图3 SDWPI自相关一偏自相关分析图

通过以上对模型的时间序列特征分析，可知WPI经过自然对数一阶差分后，序列趋势消除，进过一阶季节差分，季节性基本消除，故而选用ARMA（p，q）模型，现在观察图3 SDWPI自相关一偏自相关分析图，偏相关系数在滞后一期时不为0，在k>2以后都处于95%置信区间内，说明序列的偏相关函数具有截尾性，所以P可以取1，2；从自相关分析可知，q可以取0，1。考虑到AR模型是线性方程估计，相对于MA和ARMA模型的非线性估计容易，故用较高阶的AR模型替换过相应的MA模型。综合考虑，可供选择的（p，q)组合为（1，1）、（2，0）、（2，1)、（3，0）。

通过上述模型的识别，确定了可供选择的（p，q)组合，现运用AIC准则选取最优的（p，q)组合。AIC准则是在模型参数极大似然估计的基础上，对模型的阶数和相应的参数同时给出一组最佳估计。一般来讲，在给出不同模型的AIC计算公式基础上，选取AIC达到最小的那一组阶数为理想阶数[3]。用Eviews6.0完成这一过程，将模型相关检验结果汇总见表1所示。

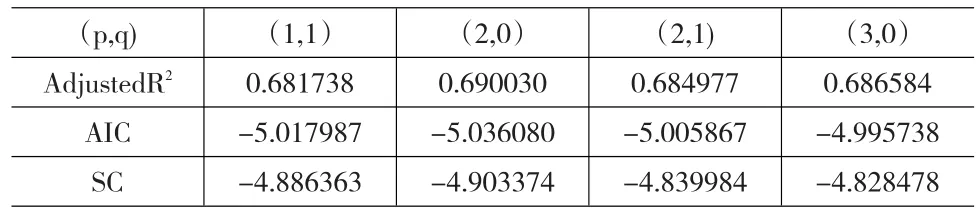
表1 各模型检验结果

经检验，四个模型的滞后多项式倒数根都落入单位圆内，满足ARMA过程中平稳条件及可逆条件。各模型残差都满足独立性假设，模型拟合较好。比较表1中四个模型的检验结果。第二个模型AIC值为-5.036080，SC值为-4.903374与其余三个模型相比其值均小，且第二个模型的可调整系数为0.690030，也优于其他三个模型的可调整系数。由此可以得出，模型ARMA（2，0）比其他三个模型的拟合效果好，因而选择第二个组合模型即ARAM（2，0）模型相对较好。通过检验得到模型ARMA(2，0)的估计结果见表2所示（见下页）。

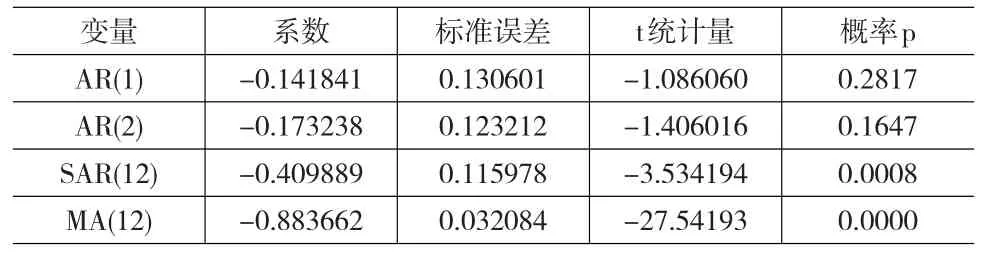
表2 ARMA（2，0）模型的估计结果

由表2写出模型ARMA（2，0）的估计方程式为：

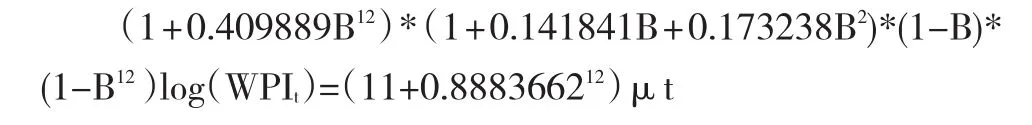
对上述模型进行统计检验分析得到，ARMA(2，0)模型的AR部分的倒数根，都小于1。因此，可以认为所估计的ARMA(2，0)模型是平稳的且是可逆的。

对方程进行估计后，对ARMA（2，0）模型的适合性进行检验，即对模型的残差序列进行白噪声检验。若残差序列不是白噪声序列，意味着残差序列还存在有用信息没被提取，需要进一步改进模型。通过对残差序列进行 χ2检验对所估计的模型ARMA（2，0）的残差进行自相关检验，残差样本的自相关函数都在95%的置信区域以内。自相关函数对应的概率p值也大于检验水平0.05，因此不能拒绝原假设，即可以认为模型ARMA(2，0)模型估计结果的残差序列不存在自相关，也就是说估计结果是有效的。

利用以上建立评价识别后的模型ARMA（2，0）对2015—2020年的全国农产品批发价格预测指数，结果如表3所示。

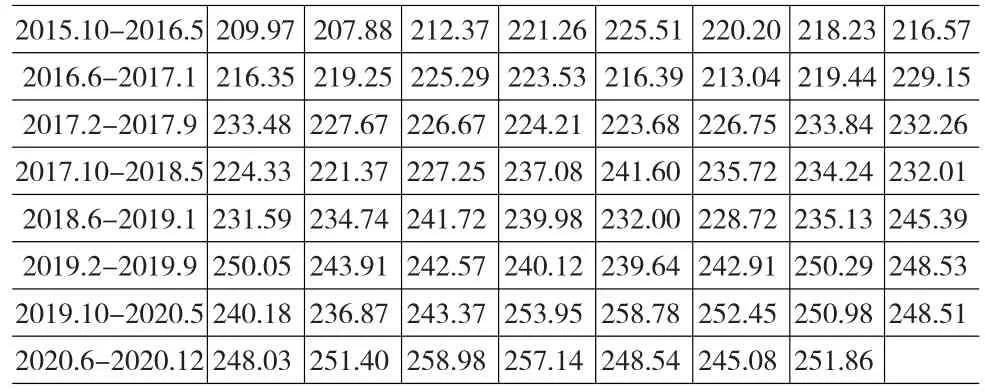
表3 2015—2020年预测结果

将ARMA模型（2，0）预测出的2015—2020年的全国农产品批发价格总指数值与实际值进行对比，得到图4，根据图4不难发现2015年1月至2015年9月的全国农产品价格总指数预测值虽然与实际值有些差距，但是差距却不是很大，这更进一步说明建立的ARMA（2，0）模型是合理的。

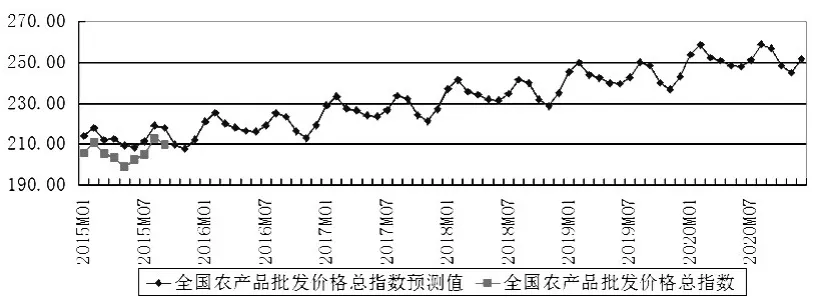
图4 全国农产品批发价格总指数预测值与实际值对比图

根据表3与图4可知，2015年9月至2020月12月全国农产品价格指数处于波幅不大的周期性上行波动之中。

3 特征分析

根据以上数据，进一步对2015—2020年我国农产品市场价格分析，首先运用CensusX12季节分解法，进行趋势循环序列（TC），季节性因素（S）和不规则因素（I）三大因素时间序列分析，然后运用H-P滤波法将趋势循环时间序列（TC）进行再分解，分解出趋势序列（T）和循环序列（C），根据原预测时间序列以及分解出的序列进行农产品市场价格的波动特征分析。

利用CensusX12季节分解方法将2015—2020年全国农产品批发价格的季节性因素分析如图5所示。图5可知，每年初的1月至4月农产品市场价格波动处于“波峰”状态，5月至6月处于“次波谷”状态，7月至9月处于“次波峰”状态，10月至12月处于“波谷”状态。表明季节性因素对农产品价格波动的影响存在显著差异，不过从波动轨迹看其季节性影响具有重复性，亦即农产品价格波动的季节性具有年周期同季节性特征。

图52015 年1月至2020年12月全国农产品批发价格总指数的季节性因素（S）曲线

利用CensusX12季节分解方法将2015年1月至2020年12月的全国农产品批发价格的趋势循环序列分解出来，并用H-P滤波法将TC分解成趋势序列（T)和循环序列（C)得到图6和图7。

图6显示的是经过季节调整和趋势分解后的全国农产品批发价格总指数。由图6可以看出，2015年1月至2020年12月全国农产品批发价格总指数成线性平稳增长趋势。全国农产品批发价格总指数的拟合优度为1，说明2015年1月至2020年12月全国农产品批发价格总指数上涨存在客观规律。

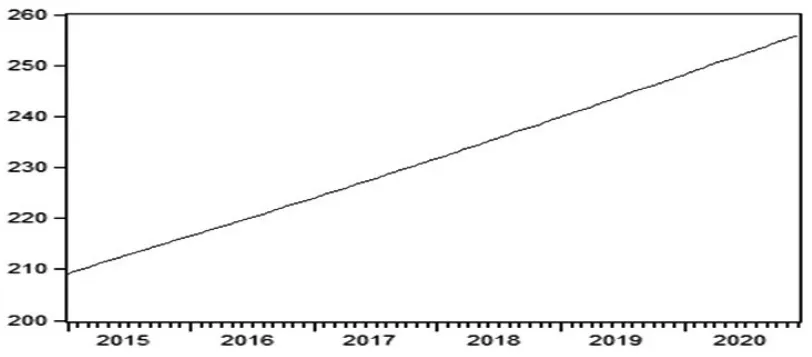
图62015 年1月至2020年12月的全国农产品批发价格总指数趋势图

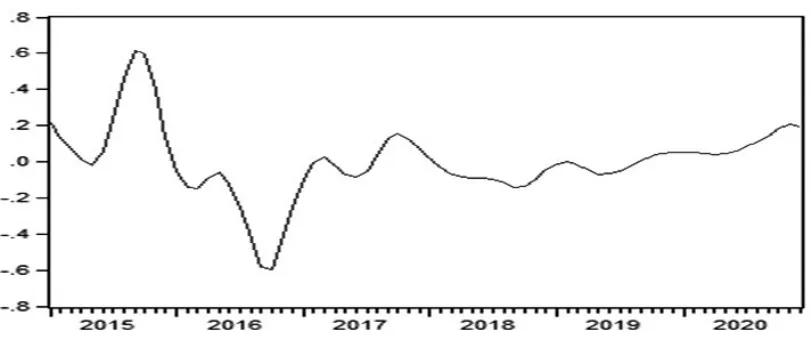
图7 2015年1月至2020年12月的全国农产品批发价格总指数循环序列图

根据图7和一个完整的周期是从波谷（峰）开始上升（下降）到波峰（谷）以后又恢复到波谷（峰），具有明显的上凸（下凹）形态的波动周期划分原则，将预测出的2015年1月至2020年12月的全国农产品批发价格总指数波动大致分为6个周期，如表4所示，周期开始于2015年5月，止于2020年4月。

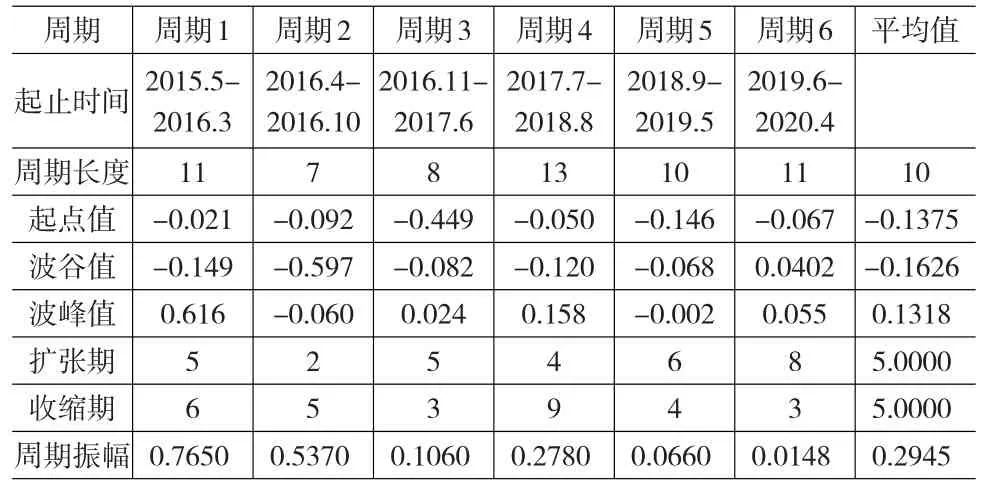
表4 2015年1月至2020年12月全国农产品批发价格总指数周期划分

从周期的扩张期和收缩期分析，2015年1月至2020年12月农产品市场价格波动轨迹中除了周期1中的扩张期与收缩期存在对称性特征以外，其它周期的扩张与收缩期存在着非对称性特征。从周期振幅比较分析，周期1和周期2的振幅比较大，分别达到了0.765和0.537；周期3和周期4的振幅居中，周期5和周期六的振幅比较小。将分析结果与图7和表4进行对比发现，处于价格上涨期的周期振幅比较大，处于价格回落期的周期振幅比较小。

利用CensusX12季节分解方法将2015年1月至2020年12月的全国农产品批发价格的随机性序列（I）分解出来，如图8所示。

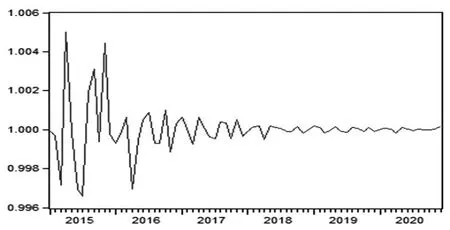
图8 2015年1月至2020年12月的全国农产品批发价格总指数不规则因素图

不规则随机波动序列是一种没有规律且不可预测的波动。随机波动往往是由偶然因素引起的，如地震、旱灾、政策、战争等。由于采用的是乘法模型，如果随机性因素I等于1，表明随机性因素对农产品批发价格总指数没有影响；如果随机性因素I小于1，表明随机性因子会拉低农产品批发价格总指数；如果随机性因素I大于1，表明随机性因素会推高农产品批发价格总指数。根据图8可知，2015—2016年，随机性因素对农产品批发价格总指数的影响比较大，2017年开始，随机性因素的振幅较小，波动幅度逐渐变缓，随机性因素逐步接近于1，趋于稳定，表现出常态。

4 结论

本文分析表明：经济新常态下我国农产品价格波动整体呈现周期性上升态势，农产品价格波动的季节性和周期性特征明显，农产品市场价格波动虽然总会伴随着随机性因素的影响，但其影响总体上处于衰减态势。因此，经济新常态下促进我国农产品市场有效运行需要谨防季节性和跨周期性的内外冲击。相关政策的设计既要目标于市场波动周期运行的稳定性，又要目标于市场波动周期更迭的连续性。周期运行的稳定性有利于衰减中国农产品价格短期波动的季节性和不规则性，防止农产品市场波动的动荡性；周期更迭的连续性有利于提升中国农产品价格跨周期波动的平稳性和预期性，规避农产品市场长期波动的随机性。

[1]任伟宏.农产品市场预测方法探析[J].中国农学通报，2011，27(26).

[2]易丹辉.数据分析与Eviews应用[M].北京：中国人民大学出版社，2014.

[3]薛冬梅.ARMA模型及其在时间序列分析中的应用[J].吉林化工学报，2010，27(3).

[4]罗光强.中国农产品价格波动与调控机制研究[M].北京：经济科学出版社，2014.

[5]钱克明.我国主要农产品供求形势与市场调控的对策建议[J].农业经济问题，2012，(12).

[6]李国祥.我国农产品价格波动分析及其调控思路[J].农村金融研究，2011，(8).

[7]常伟.农产品价格异常波动的机理分析与对策探讨[J].价格理论与实践，2011，(3).

（责任编辑/浩 天）

F201

A

1002-6487（2016）21-0083-04

国家社会科学基金资助项目（15BJY094）；教育部人文社会科学基金资助项目（10YJA790129）

罗光强（1963—），男，湖南湘乡人，教授，博士生导师，研究方向：产业经济。

周 黎（1990—），女，湖南邵阳人，硕士研究生，研究方向：产业经济。