多目标智能加权灰靶决策模型构建及应用

2016-12-20尹庆伟

统计与决策 2016年21期

关键词：局势灰色决策

童峰，尹庆伟

(1.四川外国语大学社会学系，重庆 400031；2.河北金融学院会计系，河北保定 071000）

多目标智能加权灰靶决策模型构建及应用

童峰1，尹庆伟2

(1.四川外国语大学社会学系，重庆 400031；2.河北金融学院会计系，河北保定 071000）

经济水平的提升带动了更为复杂的社会问题决策矛盾，特别是多问题和多方向性筛选对于均衡化决策的重要性日益凸显，而多方案性问题的解决是以其更为复杂前提下的决策均衡化为主要标志的，为此，文章从均衡方案决策的设置、事件以及决策集的参数构建探讨了均衡方案的模型设置与优化，并通过多目标智能加权灰靶决策的均衡方案来形成区间数型属性值和TOPSIS法的筛选，最后结合实证算例的方式论证了通过多目标智能加权灰靶决策的可行性与实践轨迹。

多目标；智能；加权灰靶；均衡决策；方案决策

0 引言

随着经济社会生活越来越倾向于复杂化以及问题解决影响机制和因素复杂化程度的加深，每个决策主体都面临更为复杂的决策过程以及方案筛选。特别是在经济社会步入全面发展阶段，发展中国家的资源、环境等要素成为制约生产合理进步的重要制约，这就要求人们运用科学合理的方案筛选，来逐步比对并优化生产过程中的各项组合决策。而同时，社会生产力的进步和产业细分与专业化水平程度提升都在一定程度上促进了生产力发展，也同时形成了更为复杂的决策要求与矛盾问题。这就要求决策主体以更为全面和科学的决策支持体系，形成符合事物发展规律的科学决策。多目标智能加权灰靶决策融合了基础灰色决策的优势，并突出了其作为决策支持的方案比对扩展属性观测、多目标和多任务决策体系的决策值确立，因此以多目标智能加权灰靶决策为基本模型，进行决策层构建，并通过灰色关联与TOPSIS法，进行进一步的多目标背景下的方案均衡化筛选应用。本文从多元决策的比较角度出发，按照均衡方案筛选的各个竞争性观测点进行基础的灰色关联与TOPSIS的联合验证，并通过区间数型属性值和TOPSIS法的筛选来确保多重决策检验的稳定性，并最终结合算例证实了多目标智能加权灰靶决策的应用合理性。

1 基于灰色原理的灰靶决策模型及其构建

1.1 灰色原理在决策模型中的应用

一般而言，针对决策的灰色模型主要选定均衡决策方案为围绕事件a的方案集，即E={e1，e1，...，em}，那么由此可以确定相应的基本事件发生集为：

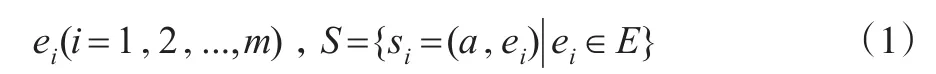
其对应事件不发生所形成的局势集为：

同时，比较该项事件在灰色模型下发生或不发生的效果值，以及由此形成的基本灰色模型和多目标只能加权灰靶决策模型形成的决策情况，即：

其中，i和 j的取值至少在3以上，以确保事件发生或不发生对立情况发生的概念影响。

1.2 灰靶决策模型的构建

结合上述对于多目标智能灰靶决策在事件发生的综合效应中，设定上述式（3）所表示的项目发生联立方程组的参变ωi、vi以及ωj、vj的活动区间为[0，1]。

根据以上分析，可以凭借灰色理论进行一般事件的决策判别，但是当同一项目出现多层事项，尤其是存在多项指标需要决策的时候，会形成时间目标效果的衍生影响。因而，研究针对基础灰靶决策模型进行基于效果测度以及事件发生目标效果，并将对应事件的上下限，这里将事件的发生与否定义成多目标智能灰靶决策中靶以及脱靶，具体过程如下：

第一步，事件及其决策集的构建。

首先，对于任何一个多目标智能灰靶决策的确立需要有基础事件、对策集、目标组合或单一目标以及决策集与映射后的目标效果，确定事件集以及对应的决策集，即对应研究范畴内的样本发生的全体事件集合：E={e1，e2，e3，...，em}，且其对应的决策集为D={d1，d2，d3，...，dn}，这一假设类似于基本一般智能灰靶决策，但根据上述分析，事件的发生存在多项目，也即是多项局势交叉可能，为简化这一过程，将这种交叉局势表述为两项局势对应决策的交叉笛卡尔集，即：

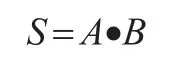
由此可以获得对应上述式（3）的决策集为：接着，确立围绕多目标的决策在效果样本上以映射方式获取的目标效果，即：

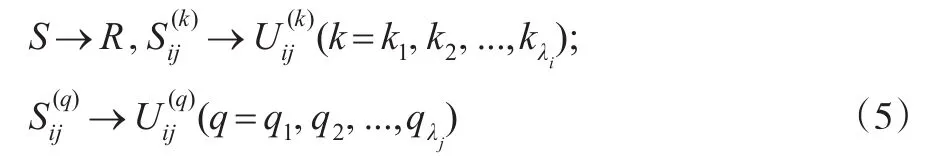
同时，可以将这种仅限于两目标决策的映射模式推广至真正意义上的多层，则相应的目标效果判定为：

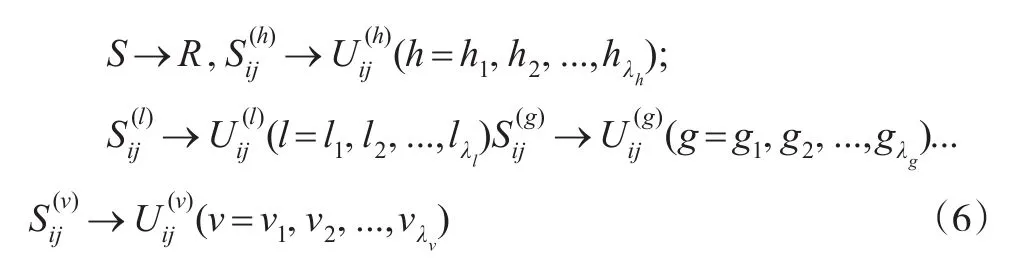
第二步，依据专家评测意见构造权重矩阵。

根据上述分析，假定多目标智能加权灰靶决策存在m类事件或事件对应局势，则令上述多目标体系下的待选方案P={P1，P2，...，Pm}，则在多目标背景下进行智能决策的均衡关键在于前述指标级的构成，基于上述分析，决策样本集表述为：，因此结合相应的决策样本与专家意见，表述局势情况的矩阵可导出相应的决策矩阵：

再次，对中间变量的累积获取最终的式（6）进行目标函数值的局势转化测度。

2 多目标分类加权灰靶效益目标分析

首先，根据多目标智能加权的灰靶靶向结合局势特征分类，即：效益型、投入型、适中型。其中效益型属于目标局势、样本效应与目标值正相关的效益目标，则其对应的两类目标智能灰靶决策的效益目标可表述为：

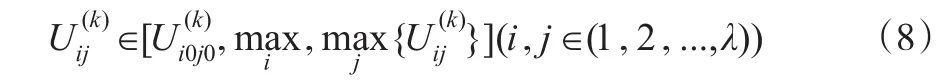
相应真正意义多目标智能灰靶决策项目则表示为：

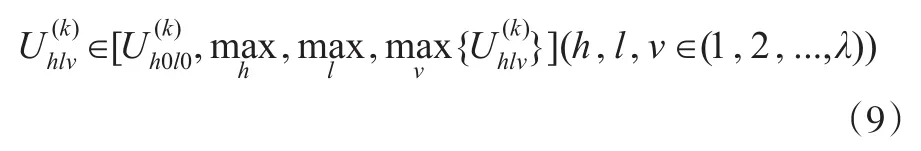
与第一类目标相反，也就是局势、样本效应与目标值恰巧负相关的，则为投入型目标：

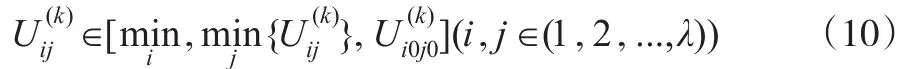
则其相应真正意义上的成本项目可通过下式获得，即：

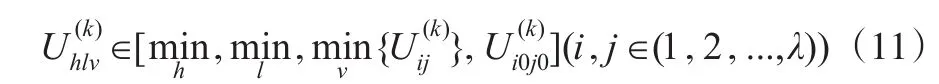
与目标的实现以及局势和效应在投入成本控制基础上，按照样本接近中值的局势定位，则为适中型目标，对照上述分析，可求得相应的两两成本项目，即：

则其相应的真正意义上的适中项目可通过下式获得，即：

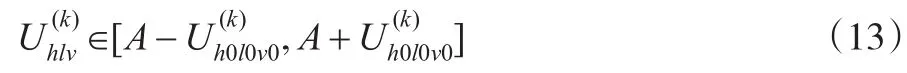
但同时需要注意的是，适中项目需要进一步设定多目标智能加权灰靶决策的上下限，即：

那么可获得对应下限为：

且对应的多目标智能加权上限应该表述为：

相应地，式（15）和式（16）可表述为：

且其对应更多多目标智能加权下限应该表述为：

由此逐步组合出适合于多类型、多目标智能加权灰靶决策的各类型项目目标效应。

3 多目标智能加权灰靶决策的均衡方案及其筛选

3.1 多目标智能加权灰靶决策的均衡方案

首先，需要指出的是根据上述步骤进行的多目标智能加权灰靶决策存在一种决策值接近的可能，而这种可能性将直接影响模型应用的区分度效果，为此研究需要进一步针对决策值接近的方案进行筛选，以获得最终的均衡方案。研究以上述效益方案为例，进行基于多目标智能加权灰靶决策的进一步均衡方案筛选验证。

其次，当对比方案对于事件而言存在决策值λ1、λ1接近且在效益目标范围内，即λ1、λ1两者满足以下条件：

则以多目标智能加权中位于灰靶末端方案的逐一比对，即(λi-λj)...(λh-λl)直至差值位于上述式（19）的设定范围，那么对应的均衡方案均集中在λh方案或者基于多目标决策的联合均衡方案λ(h·l·v)。而当多目标智能加权灰靶决策可供方案均符合上述式（19），那么形成了任选方案的决策值集，此时的均衡方案选择按照λ1、λ1中的决策值大小，也就是说对于收益型目标而言，选择所有列入可选范围的最高决策值方案，即：

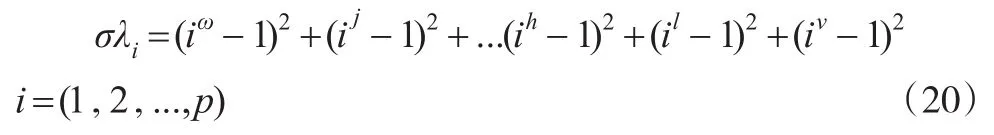
其中，ω、j、h、l、v分别为对应方案在决策值后的序号。

再次，针对多目标智能决策，研究进一步按照方差逐项比对的方法进行均衡方案筛选，即以各组选项进行相应的方案接近程度的比对，主要借助于方差来判定作为选项方案的样本变量在各种方案上的差异距离，并以方差中心距来测度若干多目标智能加权灰靶决策的供选方案的均值接近，也即是方案的现实可行拟合程度。假定多目标智能加权的决策在初始状态下，仅为简单的逻辑对立关系的两两互相决策集，即：

那么，当决策单元仅限于两个对立事件时，将上述事件以及局势对应的决策集可进行相应的数学运算，即：

相应的方向性距离函数为：

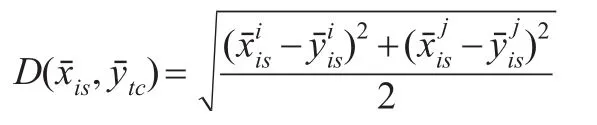
相应地，多目标智能加权灰靶决策集也有对应的决策单元求和、求差、交积项以及相应的多目标方向性距离函数，限于篇幅，不再赘述。

3.2 多目标智能加权灰靶决策均衡方案的筛选

由此，可对带检验的项目区间数型进行基于TOPSIS方法的推广，并为之后的实证验证奠定基础。TOPSIS法，又称逼近于理想解的技术，最初由Hwang和Yoon（1981）两位学者提出，该项技术的获取以设定两个虚拟方案，即最优和最劣方案，且按照实际额测度若干均衡决策方案对于上述最优、最劣方案对应的最优正向方向性距离、最劣方向性距离，并以各个方案间的方向性距离函数评估每个待选方案的优劣性。根据以上分析，研究针对最优、最劣方案集刷选，具体按以下步骤进行：

首先，设定符合基本事件或决策独立的基础据决策矩阵，即令Bˉ=(bˉij)m´n，特别是其中对应的决策值区间数bij，那么基于局势评述因子ε，可以将由此对应的决策矩阵经过转换变为适合于最佳综合预期的算数平均，即：

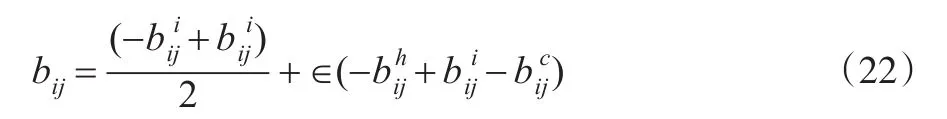
其次，研究撇除适中型而选择效益型以及成本型作为验证对象：

而相应的成本型则可以根据以下的数学关系予以折算：

式（22）和式（23）中参变量h、l、v共有1，2，...，n个迭代次序，接着研究进一步以灰色关联及TOPSIS进行相应的验证。

最后，可以获得基于事件以及局势和决策分类在上述式（20）的偏好最值差异的方案集，再结合式（20）的方向性距离测度，以h决策集为例，根据最优正向距离、最差负向距离实施适选方案的最后筛查，即：

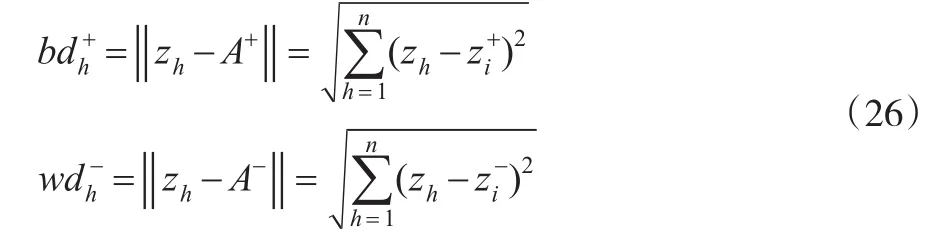
从而获得灰色关联基础上的进行TOPSIS优化的相对贴近值，即：

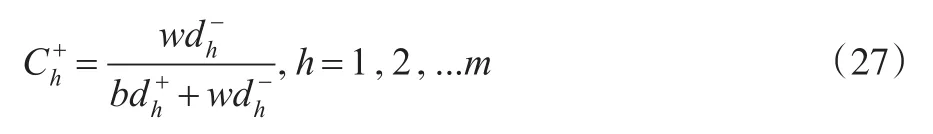
4 算例分析

我国西部地区民用沼气能项目因涉及跨国供应商协作、项目供给以及制造过程复杂程度等方面因素的影响，因此以项目招投标形式完成，其中过程为项目引进方主控工程要求，并由各供选方案提供者形成初选项目，将各初选项目信息披露于工程招投标，涉及竞选项目的各决策观测维度的信息集，并由主控方按照招投标形式决策各类因素对供选初始方案的影响。在这一过程中，西部民用沼气能项目在竞选过程中呈现出了观测维度竞争指标接近的特征，需要进行进一步的均衡决策，具体过程如下：

第一步，记作事件a1，并将对应供选5个方案分别记作b1～b5，相应对策集为：B={b1，b2，b3，b4，b5}，那么根据前述分析可知，针对此项目的多目标智能加权对策集为：

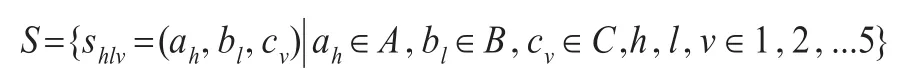
第二步，结合项目对应的常见供选方案构建相应供选方案待测指标。

一般而言，将项目供应商的各种供应方案按照质量、供货量、主体信用以及价格这四类因素记性分目标决策，其中质量主要是指产品项目的服务质量，供货量主要从项目配套建设生产以及交货进度的满足程度上予以衡量；信用则是以主体的行业前景评估、财务状况及其稳定性的角度予以评估；价格因素主要是指在项目供应期间的平均市场价格，四类决策目标对应研究中的多目标智能决策集，其相应的细分测度指标如表1所示。

表1 项目供选方案样本数据测度角度及其属性

根据上述分析，逐步确定基于各项因子权重时序在最优正向距离、最差负向距离的分析偏好，即不同程度的分析偏好按照最后待选方案与最初待选方案的时点比值q，进行对应供选方案的最优性折算，即：

而基于式（19）和式（20）的决策值，以及式（26）的最优正向距离、最差负向距离，形成关于时点比值的等额权差Dω，其计算过程为：

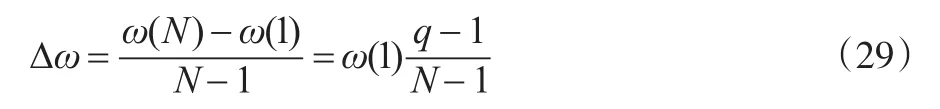
根据上述分析注意获得项目对应各供应商项目的定量化指标样本数据，即供应商项目的供应价格与供应价格对应表1的测度角度可获得如表2的样本数据。

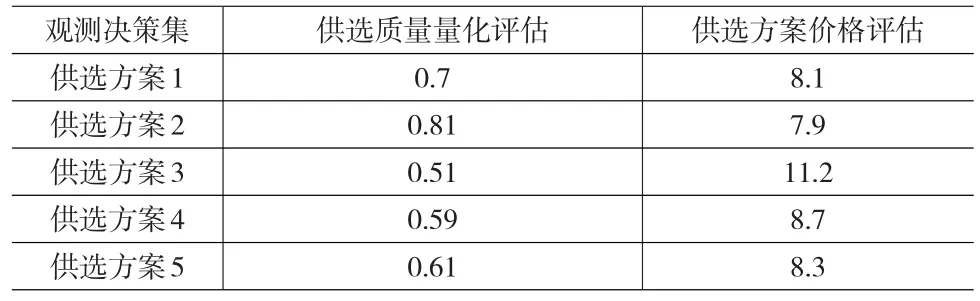
表2 供选方案定量化指标样本

基于以上样本数据的定量化评估，研究可获得基于灰色关联权重，并按照下式逐步进行折算：

即结合多目标智能灰靶决策初始化矩阵（32）利用极差变换法获得供应项目的供应价格及供应质量的规范化加权矩阵（33）：

根据（12）—式（18）求得针对本项目5招投标方案相应的等差递增权序列所对应的正向以及负向Euclid距离，所获正负向方向性距离结果如表3所示。

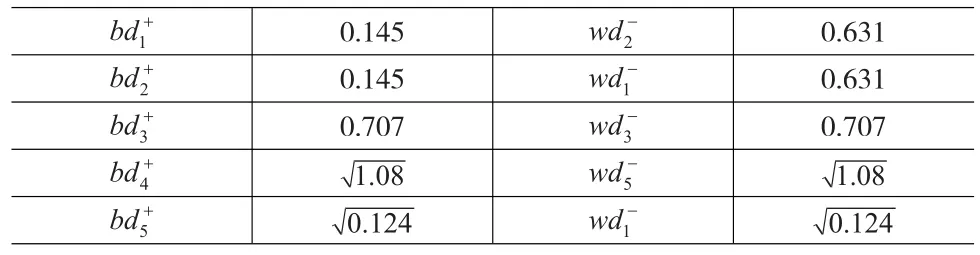
表3 等差递增权序列的正向以及负向Euclid距离

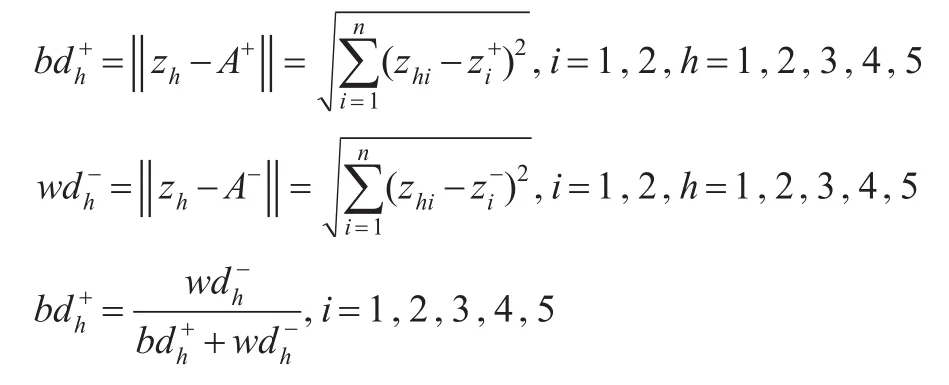
因此根据上述式（26）和式（27）可获得对应的最优正向距离以及针对TOPSIS优化基础上的相对贴近值，即：

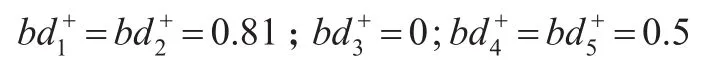
第三步，结合TOPSIS的验证关联排序及关联性分析。

研究主要利用待估项决策需要以方向性距离进行比对分析，最终以比对分析为依据，逐步围绕供选方案与其方案在投入与效率间获得平衡，构建起适用于自身最有用的对策信息集，也就是灰色关联基础上的TOPSIS分解。如表4所示：

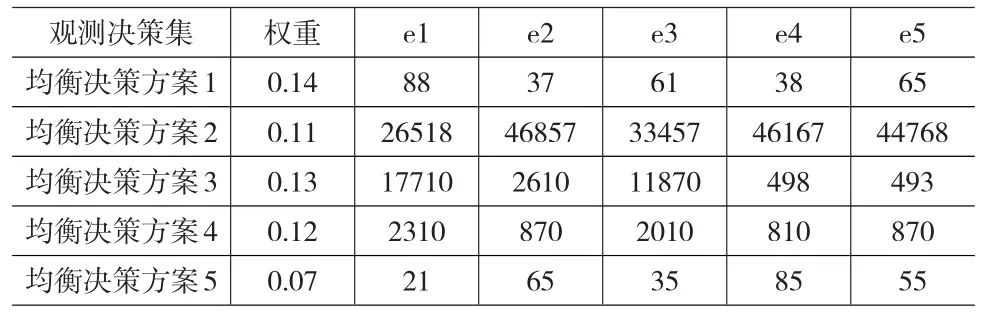
表4 基于灰色关联的TOPSIS分解

首先，运用灰色关联理论求得供选方案1～5的综合观测集效果，即依据上述式（3）和式（6）进行相应的多目标智能加权决策模型的决策映射目标效果：

其次，根据式（31）的灰色关联权重则为：

V=[v1，v2，v3，v4，v5]=[0.98，0.67，0.71，0.65，0.61]

根据前述式（3），令α=0.5，那么据此获得的对应局势集阵为：

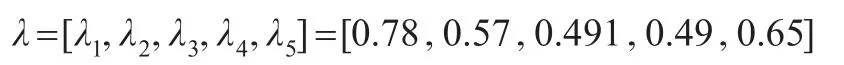
再次，获得多目标智能加权决策模型的供选方案在决策映射目标、对应局势集阵、相对方向性距离等指标上的总体排序为：供选方案1、供选方案2、供选方案5、供选方案3、供选方案4。

最后，研究就多目标智能加权决策模型的供选方案的观测分析维度扩展至决策映射目标、对应局势集阵、相对方向性距离等多目标体系，并进行基于灰色关联以及TOPSIS的验证：

根据决策值λ1、λ1接近且在效益目标范围内的比对，依据式（19）折算均衡阈值结果为0.2，由此多目标智能加权决策的供选方案均衡决策值σλ1～5分别如上表4所示。

根据上述分析，研究将本项目初始供选方案排序为：供选方案5、供选方案1、供选方案2、供选方案3。

5 结论

研究针对当今经济社会发展过程中相对复杂的项目方案筛选及其决策进行了实证分析，均衡决策同样适用于较低量样本数据以及较为集中和均衡的观测集样本对应的多目标决策问题，特别是存在多角度以及多目标方案特征时，针对决策管理进行了智能加权灰靶与关联决策的均衡，树立了多角度多目标决策问题的通过结合灰色关联以及TOPSIS方法的应用。同时需要指出的是，本研究可以在样本量相仿以及类似的供选方案观测指标具有接近程度的案例中得以应用。

[1]Kannan D，Jabbour A B L D S，Jabbour C J C.Selecting Green Suppli⁃ers Based on Gscm Practices：Using Fuzzy TOPSIS Applied to a Bra⁃zilian Electronics Company[J].European Journal of Operational Re⁃search，2014，233(2).

[2]Hwang C L，Yoon K.Multiple Attribute Decision Making.Lecture Notes in Economics and Mathematical Systems[M].Berlin:Spring⁃er，.1981.

[3]戴文战，李久亮.灰色多属性偏离靶心度群决策方法[J].系统工程理论与实践，2014，34(3).

[4]罗党.基于正负靶心的多目标灰靶决策模型[J].控制与决策，2013，28(2).

[5]谭玉叶，宋卫东，李铁一等.采矿方法优选多目标决策一致性组合权重研究及应用[J].北京科技大学学报，2014，(8).

[6]张娟，党耀国，李雪梅.基于前景理论的灰色多指标风险型决策方法[J].计算机工程与应用，2014，（6）.

[7]闫书丽，刘思峰，方志耕等.基于累积前景理论的动态风险灰靶决策方法[J].控制与决策，2013，28(11).

[8]朱丽，朱传喜，张小芝.基于粗糙集的犹豫模糊多属性决策方法[J].控制与决策，2014，29(7).

[9]马金山，孙静.基于决策者偏好的正负靶心灰靶决策方法[J].科技管理研究，2014，(23).

[10]万树平，李登峰.具有不同类型信息的风险投资商与投资企业多指标双边匹配决策方法[J].中国管理科学，2014，22(2).

（责任编辑/浩天）

F202

1002-6487（2016）21-0072-05