信息不确定条件下的风险决策研究

尹文专

(重庆科技学院 工商管理学院，重庆401331)

信息不确定条件下的风险决策研究

尹文专

(重庆科技学院 工商管理学院，重庆401331)

信息在风险决策中扮演关键角色，但决策者在现实情境中却往往无法掌握明确信息，文章试图分析实验参与者在信息明确程度不同的情境中对决策偏好的差异，以探索其与风险态度的关联性。研究发现：决策者会因信息的明确程度不同，而偏好不一样的风险决策；风险决策差异愈大，越容易在不同信息明确程度下做出相异的选择；在信息不明确情况下，决策者相对偏好较稳健的风险决策。同时，发现参与者的金钱效用和机率权重参数与信息明确程度呈现明显的相关性。

风险决策；信息；机率权重函数；Probit模型

0 引言

我们在日常生活中经常会遇到许多事件，在事件中我们常去思考每件事情所能执行的选项，探讨这些可能性会导致怎样的结果，然后决定如何去执行或者处理我们所碰到的事件，不论是购买商品、决定晚餐的菜色，甚至是决定未来要去的学校等事件中，我们都会遇到需要决策的时刻，并且做出对自身来说最为有利的选择，但是事实上每个事件所发生的机率并不一定会是十分明确的。就如在实际生活中一段时间内碰到愉快的事情或者倒霉的事情的机率，这些机率事件中，人们对于机率信息的掌握并不一定能非常精确的判断，人们至多只能通过一些外在信息的收集以及个人主观的判断，去猜测这些事情发生的可能性，事件发生的机率信息的呈现，经常是不明确甚至是含糊不清的情况。更或者，一些完全无法去预测的事件机率，人们甚至没办法通过信息去收集，而只能凭空去臆测出可能发生的机率。以一个简单的例子来说，假设有个实验，有两种情况分别让参与者去选择：情况一、箱子内的总球数为10颗球，其中里面有3颗红球。情况二、箱子内的总球数为5到15颗球之间，其中里面有3颗红球。参与者被告知两边的情况，并且当从箱子内随机抽出1颗球，若抽出来的球为红球，那么参与者可以获得奖赏。那么，参与者在情况一中，可以知道他抽中红球的机率很明确为30%，然而，在情况二中，参与者并不能很明确猜出他抽中红球的确切机率，因为他并不知道箱子内的确切总球数，他只能得知他抽中红球的机率会是20%至60%。那么，参与者评价这两组情况可能并不相同，即使在期望值的计算上可能是一样的，但是在风险决策的判断上并不一定是相同的，甚至可能在评价上会有完全不同的结果。

人们对于机率信息的模糊程度，是否会造成行为决策的影响，一直是实验经济学所十分关心的议题。本文采用实验法模拟一种经济决策，去呈现出机率刺激，并且借这些机率刺激去操弄信息明确程度的高低，仿真机率信息的明确程度，以便去了解人们在面对不同情况的信息的明确程度下，他的判断依据和风险决策是否会有所改变。在决策的评价上，是否也会有不同程度的影响。在选择时，是否会因为信息的模糊程度不同，而导致行为决策的影响。

1 风险决策实验函数设计

1.1 金钱效用函数与机率权重函数

在本文中，金钱效用函数采取幂函数(Power function)形式，函数形式如下：

其中，m代表参与者所面对决策的报酬金额，而α为参与者的金钱效用，是本文所感兴趣的参数。当α<1，表示该参与者为风险规避者；而α=1，表示该参与者为风险中立者；α>1，则表示该参与者为风险爱好者。

在机率权重函数的估计上，本文采取单一参数的prelec函数，函数形式如下：

中，p代表参与者所面对决策的中奖机率，而γ为参与者对中奖机率的权重参数。当γ=1，事实上可视为W(p)=p，代表参与者对机率的评价没有受到扭曲；当γ>1，则机率权重函数会呈现前凹后凸的倒S型；当γ<1，则机率权重函数会呈现前凸后凹的正S型。

因此，参与者对于两边的决策的期望效用，分别为如下形式：

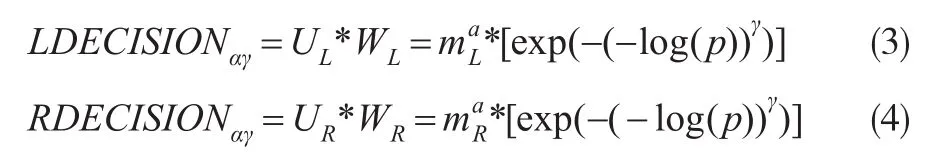
另外，本文同时也思考，模型不加上机率权重参数的情况下，参与者面对不同模糊程度之下的机率信息，对金钱效用参数会有怎样不同程度的影响。因此，本文同时也假设参与者对于两边决策的期望效用，分别为如下形式：

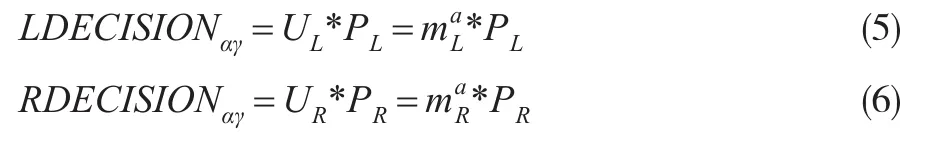
1.2 最大概似法参数估计

假设参与者在面对一对决策组合分别为PL、PR、mL、mR，那么参与者对于两边决策的评价分别是左边决策的期望效用扣除掉右边决策的期望效用，可以得到如下式子：

假设参与者对干扰项e是平均数为0，变异数为k的常态分配，可用以下来表示：

故参与者在评价每组决策时可以假定如下形式：

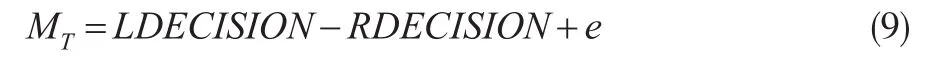
通过上述设定，可知MT为平均数μMT为LDECISION -RDECISION，变异数σMT为k的常态分配。当MT=0时，参与者对两边决策的评价应该是相同的，因此选择左边和右边的机率是相同的。当MT>0时，选择左边的机率比右边高，且MT越大，选择左边的机率就越大；反之，当MT<0时，选择右边的机率比左边高，且MT越小，选择右边的机率就越大，因此若假设选择左边决策的机率为PA，那么PA应该会遵守如下条件：

问题可以引导学生进行思考，促进学生的思维发展，高中物理教师应该设计符合学生认知能力和物理水平的问题，由简到难，通过低起点、多台阶为学生搭建起学习的“脚手架”，让学生能够顺着问题的阶梯“拾级而上”，锻炼学生的思维，让学生在问题中进行思考和质疑，发现知识的规律.教师设计具有层次性的梯度问题，让学生根据情况进行自主思考和合作探究，既能丰富教学内容，体现学生的主体地位，也能让学生的学习更加的平滑，逐步的提升学生的思维品质.

因此，可以通过这些方式，得出每一笔参与者在面对各个决策组合时选择左边决策的机率。当参与者做完整个实验后，可以得到参与者选择的结果，令参与者的选择为Y，当Y=1时，表示参与者选择了左边决策(PL，mL)的组合，当Y=0时，表示参与者选择右边决策(PR，mR)的组合。将每一笔资料取对数后相加，就可以得到最大概似函数LαγK和Lαk：

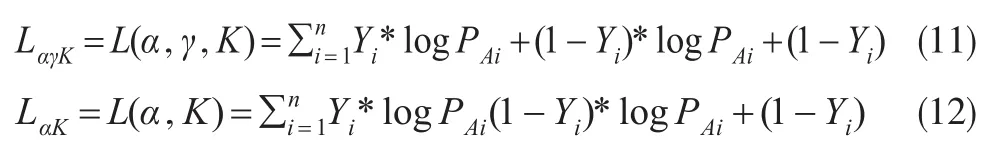
然后通过Matlab的非线性函数求根法，找出一组合适的参数组合(α，γ，K)和(α，K)可以使得LαγK和LαK分别达到极大值，即可获得参数的估计值。

2 参与者资料分析

本实验总共招收28名参与者，其中男性12名、女性16名。参与者的年龄分布在20岁至36岁之间，平均年龄为22.97岁(标准偏差为3.25岁)。参与者所接受的实验刺激皆由Matlab软件中的Psychtoolbox函数库所撰写。实验过程分成三种阶段，在第一阶段中，参与者接受实验人员的指导，进行口头上的指导，并且进行一次含有十二次试验的练习，并在听完实验说明后，填写参与者参与同意书，以让参与者了解整个实验的流程。第二阶段为正式实验，在该实验中，参与者面对9个回合，总共432次的选择试验，若该试验中，参与者较喜好左边的决策组合，则该参与者可以按下键盘的←键选择；反之如果参与者较为喜好右边的决策组合，则该参与者可以按下键盘的→键选择。参与者选择出较为偏好的组合后，经过0.5秒，程序会根据上面的机率刺激，去随机决定参与者在该试验中是否中奖，中奖机率完全依靠参与者在该次试验中所选择决策的机率刺激来决定，且跟先前试验与往后试验的选择无任何关联性。在第三阶段中，参与者将会通过程序的指示，随机抽取1个参与者在第二阶段中所回答过的432个决策试验，并且显示出当时参与者所做出的决策选择。接着程序会根据参与者在该次试验中的回馈信息，显示出参与者在该试验中所选择的决策组合是否中奖。

参与者接受三种不同的机率刺激，分别呈现出长条型、随机点及问号型的机率刺激。而资料结构上面会有两种情况，分别为RC情况和RR情况。

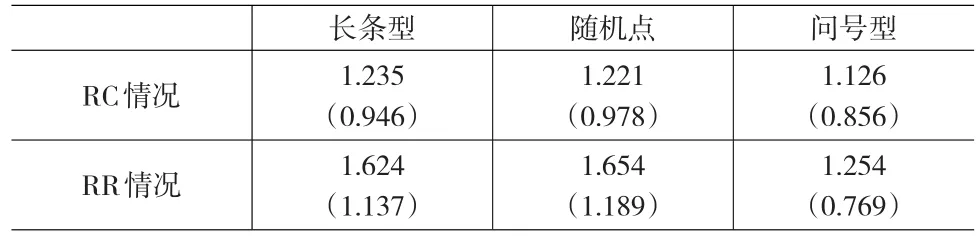
表1 参与者在不同情况下平均反应时间

平均来看，RR情况比RC情况来得久，而在回答长条型及随机点上，平均来说会比问号型来得久。事实上，参与者在面对RC情况时，只需判断其中一边的机率信息，因此在反应速度上更快。

从图1可以看出在RC部分，三组没有明显差异，但在RR部分BA和RA不一致的比例高于BR不一致的比例，甚至差距达到20%之多。

图1 两两机率刺激对照

因此，在参数的评估上主要考察随机点和长条型的机率刺激组。

3 参数分析与模型适配度分析

本文将资料剔除问号型后，以机率刺激为一个变量，以RC和RR为另一个变量，利用前文介绍的Probit模型，算出一组参数使得该概似函数最大的解。主要采用成对样本T检验来验证这两参数。在RC情况下，长条型决策为BARRC、随机点决策为RDSRC；在RR情况下，长条型决策为BARRR、随机点决策为RDSRR。

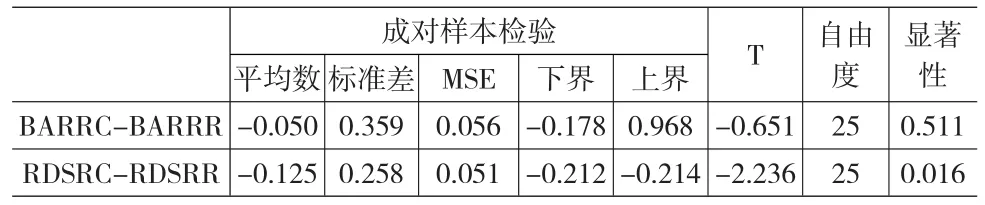
表2 长条型决策下RC和RR的不同的机率呈现，α的成对样本检验

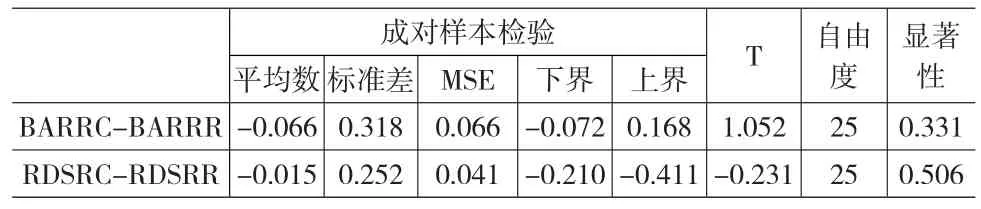
表3 随机点决策下RC和RR的不同的机率呈现，α的成对样本检验

表2中，长条型决策RC和RR的α有显著差异。表3中，不论在RC或RR情况下，参与者的风险决策都没有显著差异。

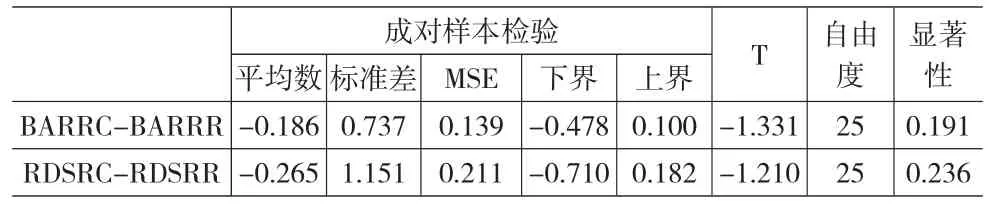
表4 长条型决策下RC和RR的不同的机率呈现，γ的成对样本检验

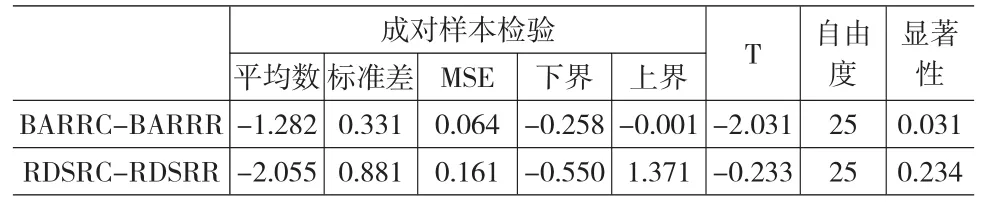
表5 随机点决策下RC和RR的不同的机率呈现，γ的成对样本检验

在γ的部分，表4中长条型决策RC和RR没有形成显著差异。表5中在RC情况下参与者决策的机率权重参数有差异，在RR情况下则无明显差异。

为了探讨参与者估计所得参数和参与者实际选择的情况是否一致，本文设定三个变量来检验这些参数的预测正确性和哪种变量有相关性。第一个变量为EV，若EV模型得到的结果和参与者回答的情况一致，则EV=1，反之则EV=0；第二个变量为EU(A)，表示考虑在Probit模型中估计两个参数(α，γ)时得到的结果和参与者的情况一致，则EU(A)=1，反之则EU(A)=0；第三个变量为EU(AR)，表示考虑在Probit模型中估计三个参数(α，γ，τ)时，得到的结果和参与者的情况一致，则EU(A)=1，反之则EU(A)= 0。

首先，通过描述统计，可以得到分别在RC和RR情况以及两种不同机率刺激下，参与者对着四组资料预测的正确比例有多少，表6即显示出在不同模型下，这四组模型正确的预测比例。

表6 三种模型正确预测参与者实际反应的比例 （单位：%）

为了详细了解参与者会受到哪种因素影响而去选择高风险的决策，令参与者在决策时选择高风险决策为Riskier，当参与者选择高风险决策时Riskier=1，反之则Riskier=0。本文将参与者的因素排除，并且将RR/RC情况、机率刺激的不同、左右两边决策小郭差距以及左右两边的期望值差距，对Riskier作回归分析得出表7。

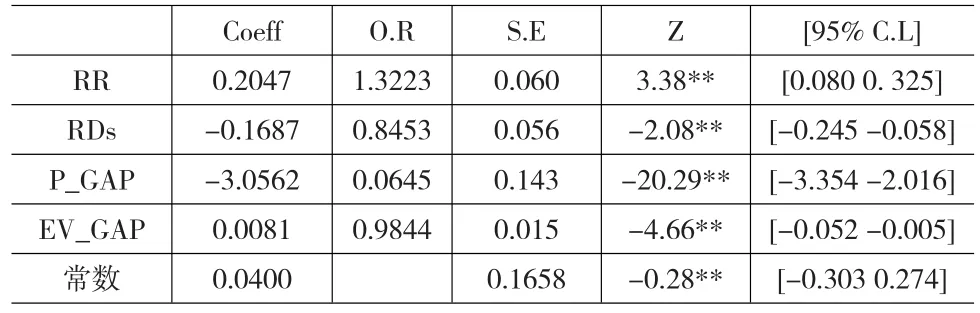
表7 参与者选择Riskier和各变量的Probit模型

当参与者面对RC模式转换到RR模式时，相对变得偏好选择高风险的决策，这反映了所谓的确定性效果；但若从长条型决策转换到随机点情景时，反而相对偏好稳健型的决策选项，代表随着参与者对机率信息的明确掌握程度降低，参与者平均而言偏好稳健型的经济决策。

在EU(A)模型和EU(AR)模型中，参与者预测能力在RC情况预测力相对来说比RR高很多，且不论随机点或者长条型都是如此，而在EV模型下，对于RC和RR情况的预测力，就不如上述来得有明显差异。

在回归分析部分，加入了机率刺激以及针对RC/RR的情况，对于EV、EU(A)和EU(AR)3个变量做3个回归，并检测出这些变量是否会和估计的正确性有相关性。

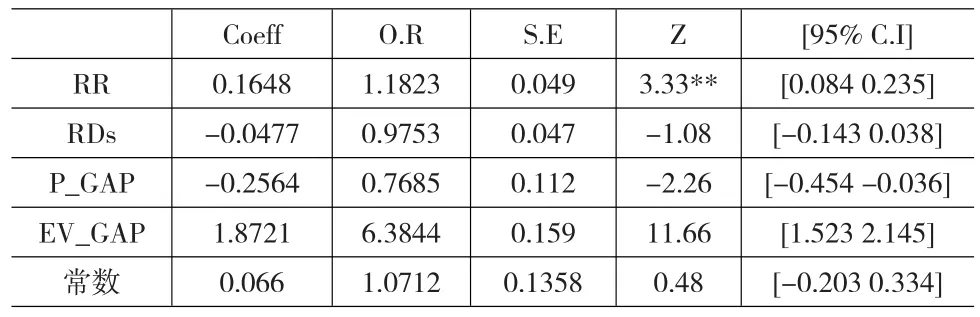
表8 EV模型估计正确性与变量间Probit模型

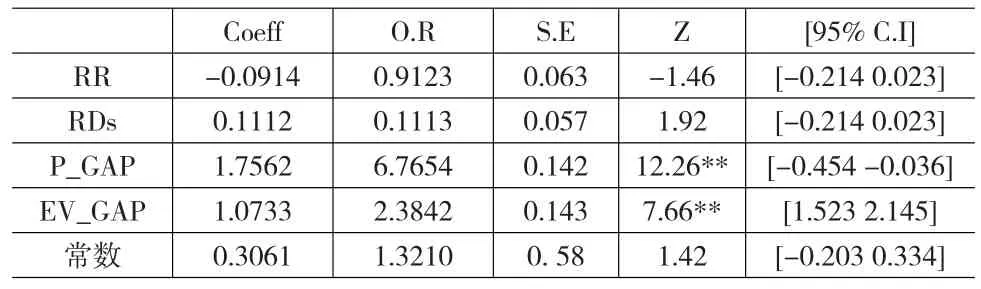
表9 EU(A)模型估计正确性与变量间Probit模型

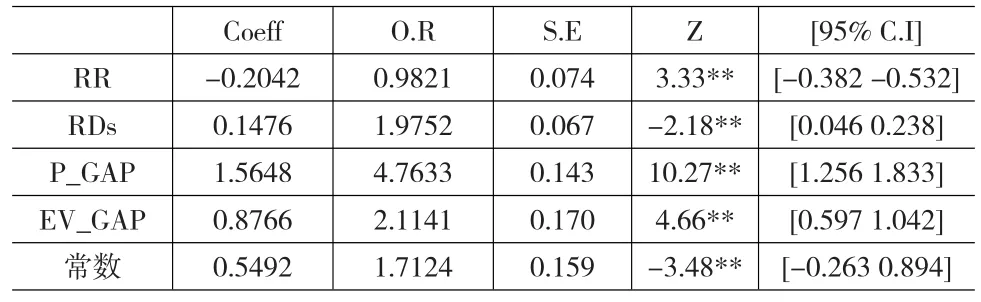
表10 EU(AR)模型估计正确性与变量间Probit模型

从表8至表10可以看出，若参与者面对的决策为RC的情况，则RR=0，而遇到RR的情况，则RR=1。而参与者若面对长条型的决策，则RDs=0，反之若参与者面对随机点决策，则RDs=1。P_GAP和EV_GAP分别是两边决策机率和期望值差距取绝对值，在RC/RR变量中，本文发现EV模型预测能力和EU(A)、EU(AR)有相反的趋势。在EV模型中，平均而言面对RR的情况模型的正确预测能力比面对RC情况更精准，且具有显著的边际效应。但EU(AR)模型则截然相反，在RC情况下，平均而言模型的正确预测能力比RR精准，且具有显著的边际效应。在EU(A)模型中虽然也有EU(AR)模型类似的效果，但并未达到显著水平。

两种模型的机率差距条件下，在EV模型中，当两者机率差距越大时，平均而言模型的正确预测能力相对较低。在EU(A)模型和EU(AR)模型中，当两者机率差距越大时，模型的正确预测能力越高。这3个模型在解释能力上，EU (AR)模型和EU(A)模型比EV模型更精准，也更能精准预测出参与者的反应。在影响预测正确性的变量上，除了机率和期望值差距外，RC/RR变量以及机率刺激的呈现上，也一定程度的会造成预测能力的正确性。

4 结论

本文探讨机率信息明确程度不同的情况下，参与者的风险态度和机率权重是否会受到影响。本文通过实验的方式发现，参与者对不同的机率信息，思考模式和想法会有很大的不同，同时本文还进一步探讨参与者的金钱效用和机率权重参数是否会因为这些变量而有所影响，也发现部分的相关性的差异。

本文了解在不同情况下回答不一致的原因，采用Probit模型去探讨参与者们在不同情况下回答不一致的状况，发现参与者在机率差距越大时，越不容易出现选择不一致的情况，反之当机率差距越模糊时，越容易产生选择不一致的情况。通过Probit回归模型，也可以得知参与者和模型的预测相符度，不仅仅受到机率差距和期望差距的影响，同时也会因为确定性效应的影响而影响预测能力。通过这些问题，本文认为机率信息的不明确程度，对于人们做出决策的影响仍然十分重要。

[1]Anderson R M，Clemen R Toward an Improved Methodology to Con⁃struct and Reconcile Decision Analytic Preference Judgments[J].Deci⁃sion Analysis.2013，(10).

[2]Hao F F，Liu Y K.Mean-variance Models for Portfolio Selection With Fuzzy Random Returns[J].Journal of Applied Mathematics and Com⁃puting，2009，(30).

[3]Ammar E."On Fuzzy Random Multiobjective Quadratic Program⁃ming，European[J].Journal of Operational Research，2009，193.

[4]卢剑峰.混合多属性群决策理想点方法[J].统计与决策，2014，(19).

[5]董坚，陈春芳，温磊.基于等级偏好占优关联系数的群决策模型[J].统计与决策，2015，(5).

[6]李太福，廖志强，辜小花，易军，葛继科.基于BPNN与ISPEA的工业决策参数稳健优化[J].控制工程，2014，(7).

（责任编辑/易永生）

C931

A

1002-6487（2016）21-0040-04

重庆市教委人文社科项目（13SKQ03）

尹文专（1978—），男，重庆奉节人，硕士，讲师，研究方向：企业管理、物流管理。