基于状态空间模型的中国财政支出季节调整研究

侯德鑫

（清华大学 五道口金融学院，北京 100083）

基于状态空间模型的中国财政支出季节调整研究

侯德鑫

（清华大学 五道口金融学院，北京 100083）

文章对中国1998年1季度至2015年4季度财政支出的时间序列构建了基于状态空间形式的季节调整模型，通过卡尔曼滤波对状态方程各量测变量进行最优估计，并通过BHHH极大似然法对模型中的超参数进行估计，得出超参数、量测变量和量测变量相关系数矩阵估计值。根据分离出的循环趋势因素和季节因素，计算季节因素绝对值变化率和HP滤波分解，得到季节因素的趋势项和循环项。通过季节因素绝对值变化率曲线、其趋势项和循环项曲线分析，得到这6个年度波动性显著的原因。研究表明，中国财政支出具有季节性特征，但在特定年份受到国内经济环境和国内财政政策的影响，季节因素具有较大程度的波动性趋势。

状态空间模型；财政支出；季节调整

0 引言

中国公共财政支出是中国宏观经济的重要指标，国内外做了大量对于其作为影响宏观经济变化的指标和其自身结构与合理性的研究。但关于其受季节趋势影响的研究较少，迄今为止，中国尚未公布包括财政支出在内的通过季节调整的经济指标数据。国内对于宏观经济指标中仅有学者利用GDP数据使用状态空间模型进行季节调整，桂文林、韩兆洲考察了GDP的季节性特征；陈飞、高铁梅分别对GDP、社会消费品零售总额、货币供应量做季节性调整分析，但都有一定的局限性。本文采用季节调整的状态空间模型研究中国1998年第1季度至2015年第4季度的财政支出数据的季节性特征，采用处于国际前沿的处理季度时间序列的季节调整方法，基于状态空间模型对我国财政支出季度数据做季节调整研究，分析我国财政支出的季节变化特征。

1 季节调整的状态空间模型

1.1 季节调整的结构时间序列模型

经济指标的时间序列通常由循环项(C )、趋势项(T)、季节因素(S)和不规则因素(I)构成。季节调整问题研究的目标是从结构时间序列中剔除季节因素的影响，分析和测定经济指标的实际运行和波动情况。季节等因素通常以不可观测成分在时间序列中出现，可基于状态空间模型估计不同状态向量进行分析和观测。

假设中国财政支出时间序列{PFEt}由趋势因素(Tt)、循环因素(Ct)、季节因素(St)及不规则因素(It)四种因素构成，其中，循环因素Ct是波动周期为几年或几十年。由于本文研究的主要内容为财政支出{PFEt}的季节调整问题，因此，将{PFEt}中的趋势因素Tt和循环因素Ct合为同一变量，即趋势循环因素TCt。结构时间序列模型的分类有以下四种模型，即加法模型、伪加法模型、乘法模型和混合模型，将时间序列{PFEt}通过加法模型表示为：

通过乘法模型表示为：

其中，TCt为{PFEt}的趋势循环因素；St为{PFEt}的季节因素；It为{PFEt}的不规则因素。St和It在加法模型中是绝对量，St和It在乘法模型中是相对量。本文采用乘法模型对结构时间序列进行季节调整。通过对乘法模型等式两端同时取log对数，可以得到两边取对数形式的加法模型：

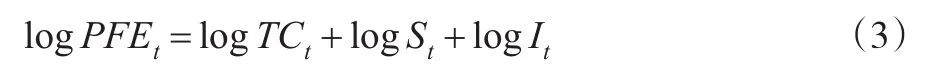
因此，乘法模型的季节调整方法可通过对数形式的加法模型得到。

经济时间序列通常是非平稳时间序列，假设时间序列{PFEt}是非平稳的，通过对时间序列{PFEt}进行d阶差分可以得到平稳的时间序列。结构时间序列的非平稳性是由其趋势循环因素非平稳引起的，趋势循环因素体现出结构时间序列的真实变动。因此，要先考察时间序列{PFEt}的非平稳性，再建立趋势循环因素TCt的表达式，将其表达式写成状态空间模型如下：

式中，L为滞后算子；βt是一个平稳时间序列；ut为零均值且方差为的随机扰动项；νt是零均值且方差为的随机扰动项。

季节因素St是以一年为周期的波动。设一年中的季节数为s（对季度数据s=4），则三角函数形式的随机季节模型可表示为：

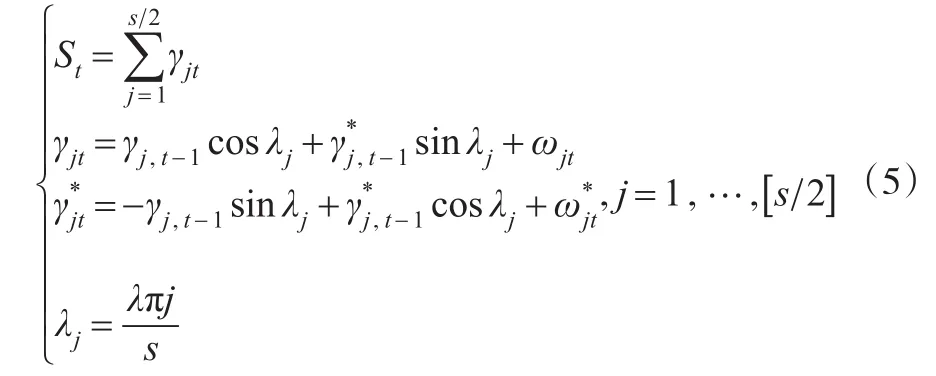
式中，ωjt是均值为零，方差为的随机扰动项。

不规则要素It为一平稳的ARMA(p，q ) 过程：

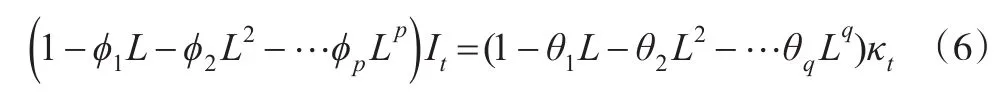
式中，L为滞后算子，κt为扰动项，ϕ1，ϕ2，…ϕp和θ1，θ2，…θp为模型参数。

1.2 季节调整模型的状态空间表示

季节调整的主要思想是将时间序列模型表示为状态空间模型的形式，再通过状态空间模型的算法估计模型中状态向量，从而实现季节调整的目的。卡尔曼滤波是在t时刻基于所有可得到的信息计算状态向量的递推过程，它是状态空间模型的核心算法。扰动项和初始状态向量服从正态分布时，通过分解预测误差来计算似然函数，进而对未知参数进行估计，卡尔曼滤波可以在计算得到新观测值时对状态向量的估计值进行连续修正。

为描述时间序列模型中各成分变量的表示形式，需要利用ARIMA模型和状态空间模型之间的等价关系，建立对应的状态空间模型。以季度模型为例(s =4)，结构时间序列模型的量测方程表示为：

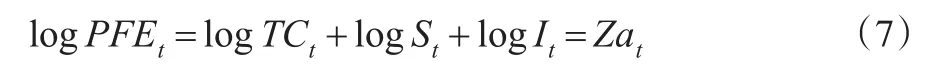
其中，状态向量at为：

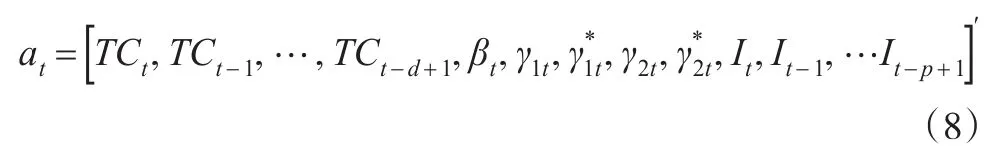
式中，p是季节因素ARIMA模型的自回归阶数。量测矩阵Z为：

1.3 求解状态空间形式的季节调整模型

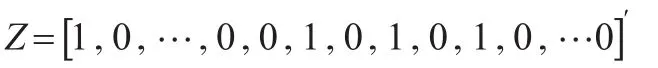
（1）通过卡尔曼滤波对状态空间模型进行估计。假设系统矩阵 Z，T，R，Q已给定，利用卡尔曼滤波对at(t=1，2，…n)的分布进行反复迭代计算，t-1期的at-1假设服从分布，此时，at的分布按下式计算得到：

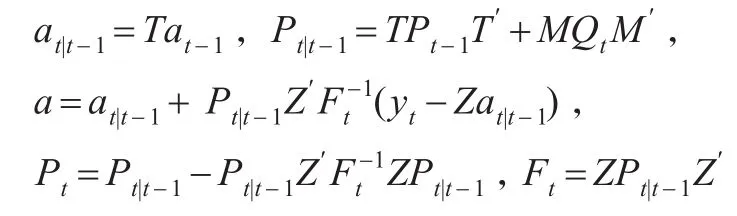
给定初值后，根据上述迭代公式可计算出at(t=1，2，…n)的分布是

（2）初值a0和P0的计算方法。将{PFEt}按时间反序排列并记作（k>0充分大），按照卡尔曼滤波方法迭代计算，得到a和P作为初值a0和P0的值。

（3）超参数估计。通常用极大似然估计法求解。{PFEt}的对数似然函数可表示为：

采用拟牛顿法求解上式，给定初始值ψ1和正定对称矩阵Π1，带入上式进行l次迭代计算得到收敛值ψl=(l=1，2，…)，ψl就是超参数向量ψ的最优估计量，进而用卡尔曼滤波进一步求出状态向量at，即求出财政支出的趋势循环因素TC、季节因素S和不规则因素I。

2 中国财政支出季节调整的检验

2.1 模型的估计和参数检验

数据选取的范围采用1998年1季度至2015年4季度我国财政支出季度数据。数据来源于中国财政部官网（http://www.mof.gov.cn/）、北京大学CCER数据库（http:// www.ccerdata.com/），获得的数据均为本年度该季度累积数据，通过ADF检验，中国公共财政支出季度数据为二阶单整时间序列。

本文实证研究所用软件为Eviews8.0。首先创造一个状态空间对象，根据式（7）及其状态方程，季节调整的财政支出状态空间模型在Eviews8.0软件状态空间窗口内定义量测方程为：log(pfe)=su1+su2+su3

将状态方程转化为回归方程的形式，通过OLS方法计算超参数的初始值，进一步带入初始值对超参数进行估计，如表1所示。

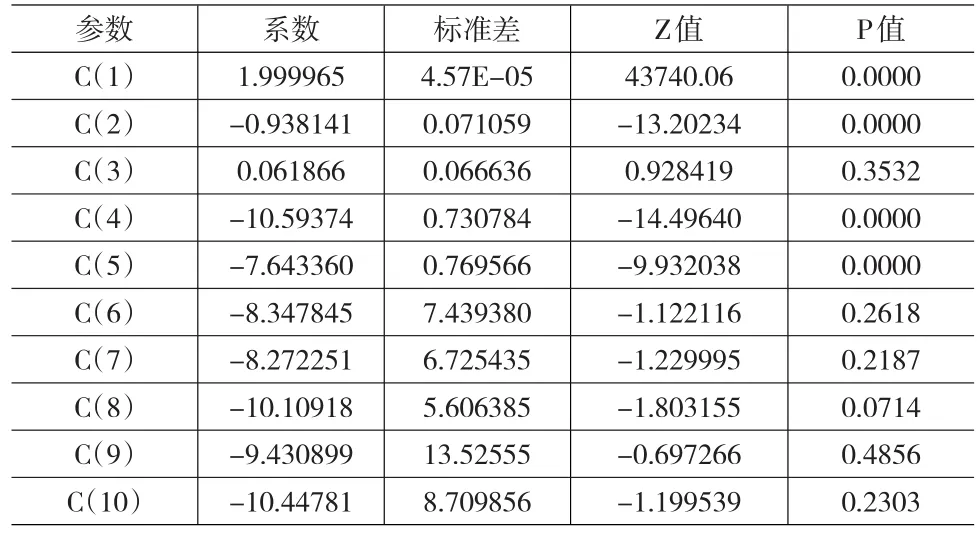
表1 中国财政支出状态空间季节调整的超参数估计和检验

表1显示了通过BHHH极大似然估计后得到的参数的估计结果。其中，表1显示了模型中超参数c（1）至c（10）的估计值、标准差、Z统计量和P值。P值中c（1）、c (2)、c（4）、c（5）均小于5%的显著性水平，c(8)小于10%的显著性水平。同时，如表2所示，模型估计的结果中还显示了最终状态向量的一步向前预测值an+1|n、均方根误差值、Z值和P值。最终状态向量对应的P值su1、su4、su5、su7均小于5%的显著性水平，其余状态向量对应P值大于5%的显著性水平。可见，超参数和最终状态向量值在模型中部分显著。此外，模型对数的极大似然估计值为36.68944，AIC、Schwarz准则和Hannan-Quinn标准分别为-0.741373、-0.425170和-0.615492均较小，可见模型总体拟合效果较好。进一步采用平滑序列的方法产生量测序列su1f-su9f。

表2 中国财政支出状态空间季节调整的最终状态估计

2.2 中国财政支出季节的调整

模型通过检验后，通过卡尔曼滤波估计得到量测变量的估计值，进一步分离出趋势循环因素、季节因素和不规则因素的估计值。考虑到模型采用的是乘法模型，还应将log形式的加法模型转化为乘法模型的形式，对三个量测变量进行指数化运算，得到相应的估计值。将使用的财政支出的季度数据和分离出的趋势循环因素估计值以同一坐标表示，如图1所示。

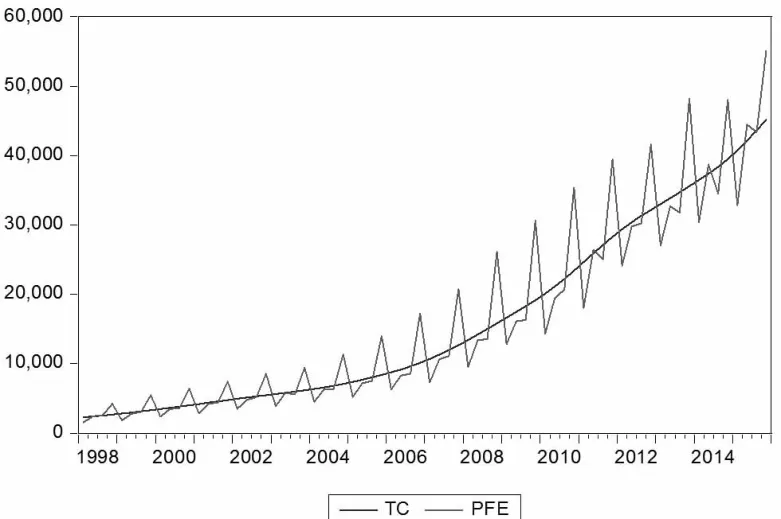
图1 财政支出的实际值及趋势循环因素

图1显示，在1998年一季度至2015年四季度这段时间内，中国的季度财政支出呈指数上升的波动性增长趋势，波动周期为一年，且每年财政支出1季度增加最小，2季度显著增加，3季度与2季度持平，但4季度财政支出呈跳跃式增长，这表明中国财政支出具有季节性特征。同时，趋势循环因素平稳增长，实际财政支出围绕趋势循环因素曲线波动，趋势循环因素平稳增长，表明我国财政支出中存在稳健的确定性趋势。从中长期看，中国政府的财政支出具有一个稳定持续的快速增长趋势，表现出典型的政府规模不断扩张的特点，即基于绝对量衡量的政府规模正在不断稳步扩大，而且这种增长趋势并没有受到经济、政治、自然等各种波动性因素的冲击的影响而有所改变。这些冲击不仅包括季节因素影响，还有1998年的特大洪涝灾害，2001年加入WTO，2003年的SARS与中国航天事业的研发，2008年奥运会的举办和年底的国际金融危机等影响。

剔除趋势循环因素和不规则因素后，可得到1998年1季度至2015年四季度中国财政支出的季节性因素（如图2所示）。图2显示出中国财政支出受季节性因素的影响程度，总体季节性因素对财政支出每年特定季度的影响程度相近，在第1季度影响较小，随后2季度大幅增加，3季度影响较小与1季度接近，但4季度的影响有显著的跳跃性增长达到最大。这种影响程度呈现出周期性波动，且波动周期为一年。图2显示，在1999年、2004年、2005年、2006年、2007年和2008年这六年中中国财政支出的季节性因素的最大波动幅度较为明显，这可能受特定年分的发生的重大事件、外界经济环境影响或是国家的政策调节因素的影响。而2009—2015年最大波动幅度逐渐降低。根据财政支出季节性因素的绝对值环比变化趋势（如图3所示），季节性因素绝对值环比变化呈周期性波动，且波动周期为一年，波动幅度相近，保持在-17%到17%之间波动。

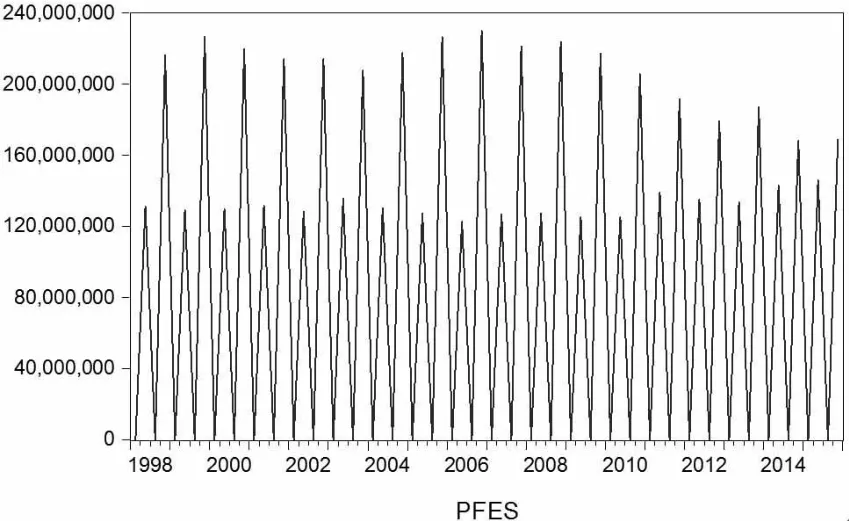
图2 中国季度财政支出的季节特征

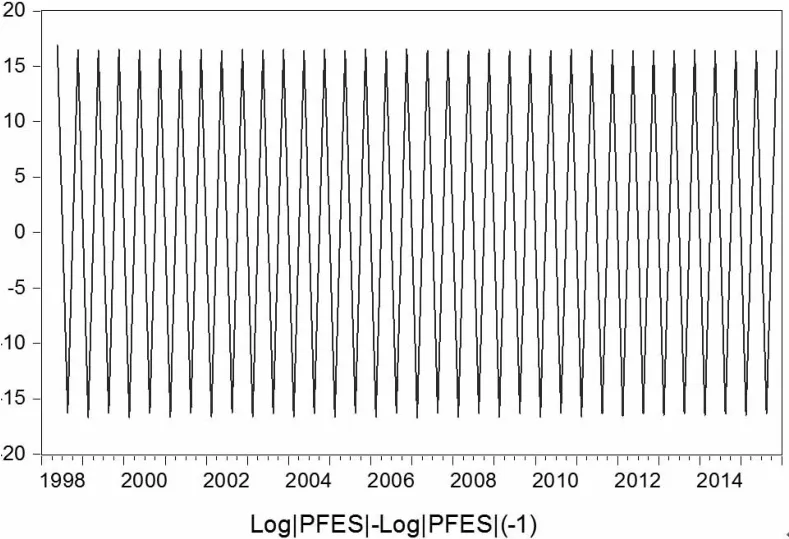
图3 中国财政支出季节性因素绝对值环比变化趋势

将得到的财政支出季节性因素进行Hodrick-Prescott滤波分解。由于是季度数据，令λ=1600，可以得到季节性因素的趋势项因素和循环因素，如图4所示。其趋势项因素趋于平缓，说明每年度季度性因素基本趋于稳定，即每年中国财政支出的季节效应基本相同。但分离出来的循环因素确具有一定的波动性，可见中国财政支出季节性因素的变化，即季节效应的大小，主要受循环因素的影响，且循环因素的波动呈规律性的跳动，可能由于财政支出受到特定经济周期或国家特定时间段内的总体政策影响，如五年计划等。

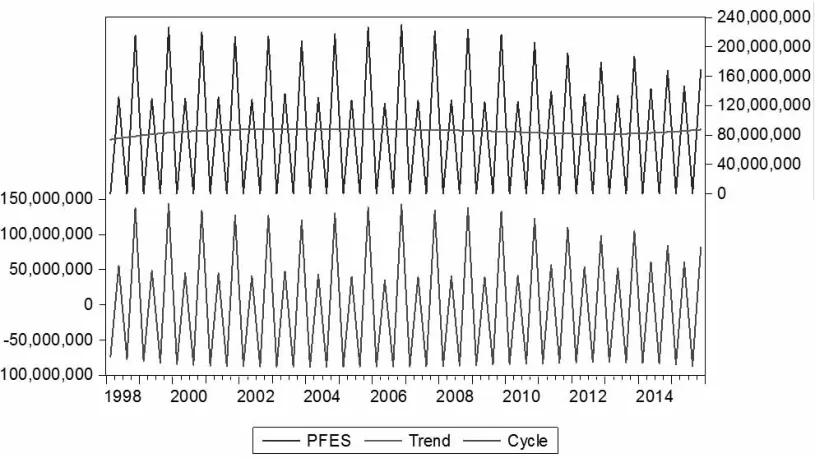
图4 基于HP滤波方法的中国财政支出季节性因素的趋势曲线与循环曲线

3 季节性因素波动原因分析

从1998年1季度至2015年4季度中国财政支出的季节性因素波动曲线（图2）看出，在1999年、2004年、2005年、2006年、2007年和2008年这6年中，中国财政支出的季节性因素的最大波动幅度较为明显，其结果表现出较大波动幅度的显著性，致使影响财政支出的季节效应变化趋势不稳定，这可能受特定年份发生的特定重大事件、外界经济环境影响或国家政策调节因素的影响。

1999年，中美两国政府签署了关于中国加入世贸组织的双边协议。我国为加入WTO制订了相关的法规政策，鼓励外商投资，大力开展基础设施建设，财政支出有较大规模的增长，1999年中国财政支出较1998年增长22.13%，从而使得财政支出的季节效应变化呈现不稳定趋势。

2004年，我国政府推行财政支出“六大重点”的政策，进一步扩大了财政支出的规模，包括“三农”、就业和社会保障、教育、卫生、科技、文化、体育、地方的转移支付等，这些投入加大了财政支出规模的波动性，使得季节效应的变化程度显著增加。

2005年，我国财政部实行稳健的财政政策，为实现保证宏观政策的稳定性，加快农业和农村经济结构调整和改革发展稳定的目标，同年减少建设型国债的发行量，增加财政收入，减少财政支出，这对于季节性效应的财政支出具有结构性冲击，也导致季节性因素的结构有较大幅度的波动。

2006年，是我国“十一五规划”实施的第一年，我国取消了农业税，加大了财政对农业的支持力度，促进城乡协调发展，进一步扩大财政支出规模，增加季节性因素的波动性。

2007年，我国经济的高速增长带动中国股市达到了繁荣的顶点，国内房屋与商品价格普遍上涨与经济过热的效应使得我国政府实行稳健的财政政策，财政支出结构有较大幅度变化，整个市场的繁荣与预期是导致政府财政政策变化的重要因素，宏观政策对财政政策的季节性冲击较明显。

2008年，国际金融危机的爆发与国家为应对危机推行4万亿的经济刺激计划对市场产生重大的冲击与影响，这导致财政支出规模的进一步扩大。奥运会的举办也使政府对国内重要城市的基础设施及文化建设加大投入，财政支出又达到了新的高峰，对财政支出的季节性增长机制有一定的结构冲击。

基于以上国内经济环境的变化和政府关于财政政策的实行等原因导致中国财政支出在这6年中波动性增长，中国财政支出的季节效应也随之有较大幅度的波动。

4 结论

我国财政支出显示较强程度的波动性增长。本文构建了中国1998年1季度至2015年4季度财政支出的季节调整的状态空间模型，通过卡尔曼滤波对模型中状态向量进行了最优估计，并通过BHHH极大似然法估计模型中的超参数。季节调整的状态空间模型成立，拟合效果良好。分离出的趋势循环因素平稳增长，实际财政支出围绕趋势循环因素曲线波动。通过HP滤波的方法从季节性因素分离出来的循环因素具有一定的波动性，而趋势因素平稳，表明中国财政支出季节性因素的变化主要受循环因素的影响。通过以上分析验证了中国财政支出的季节性效应。

本文通过季节调整的状态空间模型研究1998第1季度到2015第4季度中国财政支出的季节效应，得到的结果显示：中国财政支出具有一定程度的季节性特征，但在特定年份受到国内经济环境和国内财政政策的影响，季节性因素具有较大程度的波动性趋势。显著的季节性特征使得近18年来的财政支出在第1季度影响较小、随后2季度有一个小幅增加，3季度影响较小与1季度接近，但4季度的影响最大、有显著的跳跃性增长。同时，季节因素受外部效应导致其周期性波动，这对于国家财政政策的制定与财政部门的政策把握、投资者投资决策及时机的选取、完善和改善政府支出结构、宏观经济的稳定具有十分重要意义。财政支出的数额逐年呈波动性增长，得出基于绝对量衡量的政府规模呈不断扩大趋势的结论。

[1]严成樑，龚六堂.财政支出、税收与长期经济增长[J].经济研究，2009，(6).

[2]赵文哲，周业安.基于省际面板的财政支出与通货膨胀关系研究[J].经济研究，2009，(10).

[3]李永友.中国地方财政支出规模的膨胀趋势与公共管理成本[J].经济学，2009，(10).

[4]贾俊雪，郭庆旺.市场权力、财政支出结构与最优财政货币政策[J].经济研究，2010，(4).

[5]陈守东，杨东亮.国财政支出不确定性对居民消费影响的实证研究[J].数量经济技术经济研究，2009，(9).

[6]桂文林，韩兆洲.基于状态空间模型的中国季度GDP季节调整（1996—2009年）[J].数量经济技术经济研究，2011，(7).

[7]陈飞，高铁梅.结构时间序列模型在季节调整方面的应用—与X-12季节调整方法的比较分析[J].系统工程理论与实践，2007，(11).

[8]高铁梅.计量经济分析方法与建模—EViews应用及实例（第二版）[M].北京:清华大学出版社，2009.

（责任编辑/刘柳青）

F810.45；0212

A

1002-6487（2016）21-0029-04

侯德鑫（1992—），男，黑龙江哈尔滨人，博士研究生，研究方向：金融经济学、数量金融学。