空间索网天线展开递推动力学建模方法研究

刘付成,孙宏丽,朱东方,孙 俊

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109)



空间索网天线展开递推动力学建模方法研究

刘付成1、 2,孙宏丽1、 2,朱东方1、 2,孙 俊1、 2

(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109)

针对大型空间可展开天线自由度多、非线性强特点，为对其展开实施有效控制，提出一种周边桁架空间机构的多自由度系统快速递推建模方法。用有限段方法处理杆件弹性部分，用等效力矩代替腹杆的驱动和锁定作用，将周边桁架双重闭环构型等价为链式多体系统。对索网大型天线用空间算子代数递推建模，求解动力学响应可模拟获得天线变形的运动和所需各驱动力矩。数值算例中获取了加速段和减速段关节空间的角位移和角速度，以及关节空间驱动力矩。研究表明该法是一种高精度、高效率的动力学递推建模方法，可适于大型可展开机构的快速计算，对实际工程中天线展开的参数设计和力学分析有一定的指导意义。

空间索网天线； 展开过程； 等效力矩； 周边桁架双重闭环构型； 链式多体系统； 空间算子代数； 角位移； 角速度； 空间驱动力矩

0 引言

随着航天任务多样化，星载大型桁架式网状抛物面天线是满足移动通信、对地遥感和深空探测等空间应用的关键设备。这种天线质量小、强度高，在空间展开式天线领域也有广阔的发展前景[1]。展开过程动力学分析是空间可展结构研究的关键之一，但其几何拓扑关系复杂，杆件和节点多，机构自由度多，若用经典多体力学理论分析桁架结构的展开运动过程，未知量多、建模复杂、效率低[2-3]。另由于弹性的存在，弹性变形成为不可忽略的因素，与整体的刚性大位移存在强耦合，使展开过程的动力特性十分复杂，对其展开过程的控制涉及振动、轨迹、展开速度控制等多方面[4]。文献[5]基于多刚体系统动力学Lagrange方法，采用广义坐标法并考虑耗散力、铰链处扭簧的驱动力及索网预张力对展开过程的影响，建立了周边桁架可展天线展开过程的动力学模型，根据规划的天线展开运动得出相应的驱动力。文献[6]在可展结构中设置刚性体以有效提高展开效率，保证形状精度。文献[7]用递推动力学建模方法对星载天线机构进行了动力学分析，表明该算法可满足动力学实时仿真及控制系统设计要求。索网天线的刚度和强度主要是由桁架的竖杆提供，中间部分的拉索只用于调节网状形面精度[8-9]。商业软件虽能对索网活动节点位置进行预测，但难以进行控制应用[10]。为此，本文用刚度分析方法对天线展开过程系统参数预估及其受力状态设计进行了研究。

1 索网天线展开建模方法

1.1 基本空间算子定义

定义第k个刚体于内铰Ok处建立连体坐标系。常用基本算子有：刚性力移位算子φ(k+1,k)；为铰Ok+1，Ok间位移矢量的叉乘矩阵；Rk+1,k为第k+1，k个连体坐标系间旋转变换矩阵；第k体空间惯量质量；J(k)∈R3×3为相对Ok处的惯量张量；p(k)为第k体质心至连体坐标系原点的位移矢量；为位移矢量对应的叉乘矩阵；m(k)为第k体质量；H(k)∈Rnr(k)×6为从状态空间至关节空间的投影算子；nr(k)为第k个铰关节的自由度。

1.2 一般树形拓扑结构说明

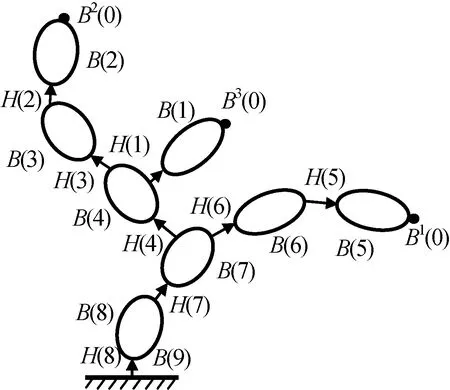
图1 一般树形多体系统拓扑结构Fig.1 Tree topology of multibody system dynamics

表1 低序体列阵

由表1可知：Pa(k)列中未出现的体号1、2、5属末端体，重复出现的体号4、7属分枝体，且重复出现数次，表明有多个分枝(此处为2个)。链式系统是树形系统的特例，因其Pa(k)=k+1。组成的低序体列阵中，不被其它列包含的低序体列阵为一个分支链，此处一个分链由体1、4、7、8组成；一个分链由体2、3、4、7、8组成；另一个分链由体5、6、7、8组成。

1.3 混合动力学递推算法

根据机构各铰关节状态，可将问题归为两类：反向动力学用于求出各驱动关节力或力矩；正向动力学用于求出各关节的角加速度。混合动力学可同时计算上述两类问题，特别适于欠驱动系统的动力学建模。索网天线铰驱动关节按预定轨迹展开，属于反向动力学问题。展开过程会影响卫星本体的姿态指向，为正向动力学问题。

混合递推与正向动力学建模相似，可包括以下步骤：按铰接体惯量方法计算系统的惯量；从顶端n体到基体1体的残余力的递推计算；正向动力学加速度计算。

a)铰接体惯量计算

P+(0)=0；

fork=1，…，n，

P(k)=φ(k,k-1)P+(k-1)φ*(k,k-1)+Mm(k)∈R，

ifk∈Ia，

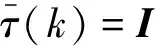
else

D(k)=H(k)P(k)H*(k)∈R，

G(k)=P(k)H*(k)(D(k))-1∈R，

K(k+1,k)=φ(k+1,k)G(k)∈R，

end if

b)冗余力递推计算

z+(0)=0，

fori=1，…，n，

ifk∈Ia，

z(k)=φ(k,k-1)z+(k-1)+P(k)×a(k)+H*(k)β(k)+b(k)+K(k)ϑ(k)，

z+(k)=z(k)，

else

z(k)=φ(k,k-1)z+(k-1)+P(k)×a(k)+b(k)+K(k)ϑ(k)，

ε(k)=T(k)-H(k)z(k)，

v(k)=(D(k))-1ε(k)，

z+(k)=z(k)+G(k)ε(k)，

end if

end loop

式中：z+(0)为分支末端体外结点处偏置力；a(k)为第k个体的哥氏加速度、离心加速度算子；β(k)为铰关节空间速度；b(k)为第k个刚体哥氏力、离心力算子；K(k)为刚体移位Kalman增益算子；ϑ(k)为关节角度；ε(k)为关节驱动递推移位算子；T(k)为状态空间力偶；v(k)为关节空间加速度。

c)系统加速度和主动力递推计算

α(N+1)=0，

fori=1，……，n，

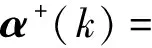
ifk∈Ia，

T(k)=H*(k)f(k)，

else

end if

end loop

式中：α(k)，f(k)，T(k)，χ(k)分别为第k体加速度、关节广义力、状态空间广义力和绝对加速度。借鉴Kalman滤波方法的计算结构，即分为向内的滤波过程和向外的递推过程平滑。通过找到满足与离散卡尔曼滤波的Riccati方程类似的微分方程实现。

2 索网天线展开过程等效模型

两个桁架单元的展开如图2所示。展开原理为连续的展开索依次穿过桁架单元的可伸缩对角杆，通过电机带动展开索收缩展开环形桁架。在结点B、D、F处各有同步齿轮1对，保证整个桁架在展开过程中的同步，即在展开过程中各矩形单元始终保持形状相同。当桁架运动至完全展开状态时，可伸缩对角杆AE、CE中的细管分别顶在顶点A、C，阻止其进一步运动，同时弦杆运动至与竖杆垂直位置，节点盖板间的填充限位件与弦杆连接件紧密接触，阻止其转动。

(a)收缩状态 (b)展开过程中 (c)完全展开图2 两个桁架单元展开Fig.2 Deploying sketch map of two truss cell

分析发现其中含双重闭环，问题非常复杂，对其进行简化，先去除腹杆，只剩下3主杆根，用等效力矩替代腹杆的驱动和锁定作用，则就转为对链式结构进行动力学建模，如图3所示。

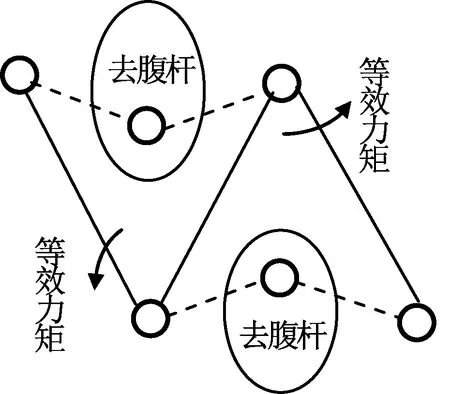
图3 用等效力矩简化Fig.3 Simplification by equivalent moment

3 数值实例

本文以周边桁架天线展开为研究对象，仿真中取参数为：弹性模量90 GPa，泊松比0.33，天线杆件直径0.035 m，每个竖杆和横杆的长度1.414 m，竖杆、横杆、对角杆密度1 900 kg/m3，卫星本体质量3 404.5 kg，质心位置(1 069，-2，2 340)，转动惯量

设卫星初始位置和速度置分别为

桁架展开过程规划经历加速-匀速-减速过程，共用时1 800 s，不同时间的规划展开铰链角速度如图4所示。

图4 规划的铰链展开角速度Fig.4 Angle velocity of joint deploying

仿真时间2 000 s，分别对50个桁架单元的桁架结构展开进行数学仿真计算，其中加速段0～200 s中部分关节铰链的驱动力矩如图5、6所示；减速段1 600～1 800 s内关节铰链的驱动力矩如图7、8所示。不同自由度展开机构展开过程所需时间：桁架单元50个为47.971 s；桁架单元100个为1 min 32.483 0 s；桁架单元1 000个为15 min 45.202 0 s。

图5 加速段关节1铰链驱动力矩Fig.5 Drive moment of joint 1

图6 加速段加速段关节10铰链驱动力矩Fig.6 Drive moment of joint 10

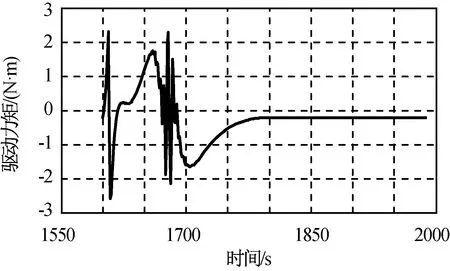
图7 减速段关节1铰链驱动力矩Fig.7 Drive moment of joint 1

图8 减速段关节10铰链驱动力矩Fig.8 Drive moment of joint 10

由仿真结果可知：按电机驱动角速度设计策略桁架能保持平稳展开。分析铰链中间处铰链展开驱动力矩，可发现在加速和降速段，铰链1处的最大力矩分别为13，2.2 N·m，最小力矩分别为约-15.5，-2.5 N·m；铰链10处的最大力矩分别为22 000，7 500 N·m，最小力矩分别为约-18 000，-7 800 N·m。总体来说，本文规划能使桁架有效展开，用递推动力学建模算法对多自由度大型桁架或天线结构的展开计算分析可行。

4 结束语

本文用空间算子代数动力学递推建模方法，将

含双闭环索拓扑结构的网动力学建模转为采用等价力矩的链式多体系统动力学模型，理论上提高了动力学模型的复杂性和计算速度。该方法适于大型可展开机构的快速计算。对实际工程中天线的展开过程的参数设计、力学性能分析具有一定的指导意义，但实用性还有待试验确认。

[1] HIROAKI T. Design optimization studies for large-scale contoured beam deployable satellite antennas[J]. Acta Astronatica, 2006, 58: 443-451.

[2] 赵孟良, 吴开成, 关富玲. 空间可展桁架结构动力学分析[J]. 浙江大学学报(工学版), 2005, 39(1): 1669-1674.

[3] 李波， 陈晓峰. 空间杆状构架式展开机构拓扑型综合与分析[J]. 上海航天， 2015， 32(1)： 25-29.

[4] 张逸群, 张志华. 柔性周边桁架可展开天线展开过程动力学分析和组合控制方法[J]. 高技术通讯, 2011, 21(7): 750-755.

[5] 李团结, 张琰, 李涛. 周边桁架可展天线展开过程动力学分析及控制[J]. 航空学报, 2009, 30(3): 444-449.

[6] 吴明儿, 项平. 含刚性体可展开结构的展开过程动力学分析方法[J]. 计算力学学报, 2011, 28(5): 653-681.

[7] 游斌弟, 赵志刚, 魏承, 等. 基于空间算子代数的星载天线机构动力学计算[J]. 兵工学报, 2011, 32(1): 85-90.

[8] 保宏, 段宝岩, 尤国强. 索网式展开天线网面精度调整的控制方法[J]. 应用力学学报, 2008, 25(1): 154-157.

[9] 杨东武, 仇原鹰, 保宏. 基于Moore-Penrose逆的索网天线预拉力设计方法[J]. 机械工程学报, 2012, 48(21): 22-27.

[10] 郭永卫, 王启明. 索网机构的理论建模与位置求解[J]. 机械工程学报, 2010, 46(1): 18-23.

[11] 刘云平, 吴洪涛, 方喜峰, 等. 移位算子及其对多体系统结构的描述[J]. 南京航空航天大学学报, 2008, 40(5): 687-691.

Study on Recursive Dynamic Modeling and Simulation of a Cable-Truss Deployable Space Antenna

LIU Fu-cheng1, 2, SUN Hong-li1, 2, ZHU Dong-fang1, 2, SUN Jun1, 2

(1. Shanghai Space Intellective Control Technology Lab, Shanghai 201109, China; 2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

Due to many degrees of freedom and nonlinearity of large deployable space antenna, a fast recursive modeling with multi-degree of freedom system of a cable truss deployable space mechanism was given in this paper in order to give a better control to the deployment. The elastic parts were treated by the finite segment, and meanwhile the driven and locking of brace were replaced by the equivalent moment. As a result, the large cable-truss double closed loop was equivalent to the chain multi-body system. Large cable-truss antenna was modeled by spatial operator algebra, and the antenna deformation motion and driven moment were obtained by computation of solving dynamic response. The spatial angular displacement, angular velocity and driving moment of the joint in acceleration and deceleration phase were gained in a sample. The study showed that the method proposed was a recursive dynamic modeling with high accuracy and efficiency which was suitable to the fast computation of large deployable mechanism. The study is valuable to the parameter design and mechanic analysis of the antenna deployment in engineering.

Cable-truss deployable space antenna; Deployable process; Equivalent moment; Cable truss double closed loop; Chain multibody system; Spatial operator algebra; Angular displacement; Angular velocity; Spatial driving moment

1006-1630(2016)04-0021-05

2015-12-13；

2016-04-26

上海市自然科学基金资助(16ZR1415700)

刘付成(1973—)，男，研究员，主要从事航天器姿态控制研究。

V443.4； TP391.9

A

10.19328/j.cnki.1006-1630.2016.04.004