星敏感器慢变误差校准方法研究
2016-12-20吴德安汪礼成刘德庆谢任远
徐 樱,吴德安,汪礼成,刘德庆,谢任远
(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109)
星敏感器慢变误差校准方法研究
徐 樱1、 2,吴德安1、 2,汪礼成1、 2,刘德庆1、 2,谢任远1、 2
(1.上海市空间智能控制技术重点实验室,上海 201109; 2.上海航天控制技术研究所,上海 201109)
对星敏感器慢变误差(LFE)校准方法进行了研究。根据星敏LFE主要是源于周期性的空间热环境变化的机理,将星敏的LFE作为周期信号,用傅里叶级数表述。用最小二乘法估算陀螺常值漂移中的周期量,再由常值漂移估计辨识出星敏LFE的参数,确定LFE傅里叶级数中正弦和余弦函数的振幅。根据傅里叶级数形式的LFE模型和估得的LFE参数,模拟产生LFE的表达式,对星敏的输出进行补偿校正。给出了星敏LFE的辨识过程。研究表明:星敏LFE补偿后,改善了姿态估计精度和陀螺常值漂移估计准确度,显著提高姿态确定系统的性能。
卫星姿态确定; 星敏感器; 慢变误差; 周期性; 空间热环境; 校准; 陀螺常值漂移; 最小二乘法
0 引言
高分辨率对地观测要求星上有效载荷能精确控制指向,或通过卫星姿态确定系统获取有效载荷光轴指向信息[1]。在星上姿态确定系统中,由星敏感器和陀螺组成的姿态确定系统精度较高,是众多航天任务的首选[2]。星敏感器和陀螺姿态确定系统的性能依赖于星敏感器的精度,星敏感器观测量中常包含LFE,LFE主要是由太阳照射角度变化产生的冷热交变的热环境,使星敏感器安装结构形变而形成的,属于星敏感器安装误差。因太阳照射角度依轨道周期变化,慢变误差可视为周期信号,其变化周期近似等于卫星轨道周期[3]。据报道,在PROBA,CHAMP,ALOS等多个航天器上都发现了周期性的星敏感器低频误差的影响[4-6]。慢变误差难以用现有的姿态确定卡尔曼滤波算法予以消除,会存在于姿态确定结果中,从而影响姿态确定精度[7]。文献[8]提出了一种慢变误差校准方法,将慢变误差建模为一阶高斯-马尔可夫过程,并将其与卫星姿态和陀螺漂移一起进行估计,其缺点是对陀螺测量精度的要求非常高。文献[9]提出一种基于多模型自适应估计的慢变误差校准方法,采用多模型自适应估计算法,根据陀螺漂移估值的频谱估计慢变误差,其局限性是多模型自适应算法复杂,计算量较大。文献[10]用具成像能力的卫星有效载荷获取地标方向矢量数据,将其作为姿态基准对星敏感器低频误差进行估计和补偿,根据有效载荷提供的一个时间序列中的地标方向矢量测量信息,采用批处理方式,基于最小二乘法估计星敏感器LFE参数,但不足之处是需要有效载荷提供数个轨道周期的地标方向矢量,工程操作较繁琐。为减小LFE对姿态确定结果的影响,本文研究了一种适于工程应用的LFE校准方法。将LFE建模为傅里叶级数,基于最小二乘算法,由陀螺的常值漂移估计星敏LFE的参数,即傅里叶级数中各正弦和余弦函数的振幅,根据傅里叶级数形式的LFE模型和估得的LFE参数,模拟产生LFE的表达式,并进行补偿。
1 慢变误差校准方法设计
星敏感器是用星光方位确定卫星姿态的精密姿态测量部件,能根据多颗恒星矢量的观测数据给出其光轴矢量在惯性系中的坐标。卫星在轨运行中受太阳照射角呈现周期性变化影响,故自身结构受热不均匀,星敏感器安装结构会受其影响而产生形变,导致星敏感器测量输出相对本体坐标系基准发生动态偏离。此外,星敏感器观测恒星过程中,其光轴所指向的天区随卫星轨道运动发生周期性变化,导致光学系统误差、标定误差和星表误差随恒星进出视场而变,也会造成周期性误差[5-6]。分析在轨卫星遥测数据认为,慢变误差可视为周期信号,而周期信号可用傅里叶级数(多个正弦和余弦函数的和)表述。
一般,用扩展卡尔曼滤波(EKF)进行姿态确定得到姿态角和常值漂移的估计结果。慢变误差会导致估计姿态角的周期性变化,因为可能将真实姿态角的周期性变化误认为是慢变误差变化,因此不能根据姿态角的估计结果对慢变误差进行辨识。
假设陀螺无安装误差,且陀螺的安装矩阵为单位阵。姿态确定过程中,陀螺的常值漂移是通过陀螺的测量值与星敏得到的角速度信息进行比较得到的。因以星敏的输出为基准,当其输出存在周期性变化时,与陀螺无周期性变化的输出比较,会导致陀螺的常值漂移估计中也包含周期性变化。因常值漂移的估计达到稳态时为常量,故可利用常值漂移的估计辨识慢变误差。
1.1 星敏感器的慢变误差
建立星敏的测量坐标系S-xyz,此处:Sz轴为星敏光轴;xSy平面与光轴垂直。一般情况下,星敏在光轴向的误差较大,在垂直光轴向的较小且十分接近,而慢变误差的性质与其类似。设慢变误差
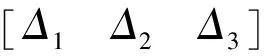
(1)
式中:Δ1,Δ2,Δ3分别对应为Δx,Δy,Δz。此处:Δi为i轴方向的慢变误差(i=x,y,z),且
Δi= vic1cos(ω1k)+vis1sin(ω1k)+
vic2cos(2ω1k)+….
其中:ω1为慢变误差基频角速度;k为序列,且k=1,…,n;vic1,vis1分别为余弦量和正弦量系数。可假设
Δ1=Δ2=Δ3.
(2)
vLFE(b)=SvLFE=-Δ1Δ3Δ2T.
(3)
因慢变误差为小量,故可近似转换为四元数形式


综合式(2)、(4)及仿真设置,取y轴向慢变误差为负,可知

(5)
1.2 慢变误差与常值漂移估计关系
陀螺误差仅考虑常值漂移和系统噪声时,陀螺输出可表示为
ωout=ωbi+b+vg.
(6)
式中:ωbi为卫星的真实角速度;b为陀螺的常值漂移;vg为系统噪声。
由星敏反解出的卫星的角速度
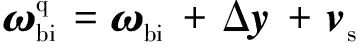
(7)
式中:Δy为由慢变误差引入的周期变化量;vs为噪声;上标q表示由星敏输出地绝对角速度。
陀螺常值漂移的滤波估计为

(8)

1.3 由常值漂移估计辨识慢变误差
卫星姿态运动学方程可表示为
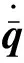
(9)

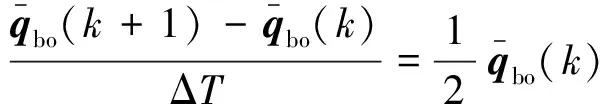

(10)



(11)
简化问题,暂不考虑其他噪声影响,只考虑慢变误差,有
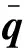
(12)
设卫星的真实姿态角为[0 0 0 1]T,则
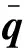
(13)
将式(4)代入式(13),可得

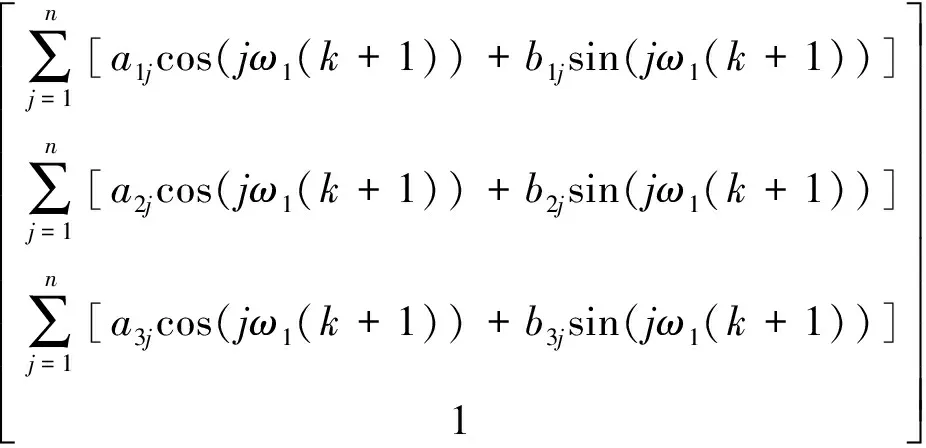
(14)
式中:ω1为周期量的基频,与轨道角速度为相同量级,因此ω1很小。将式(14)中的正弦量展开近似有
ajcos(jω1(k+1))+bjsin(jω1(k+1))≈
bjsin(jω1k)+bjjω1ΔTcos(jω1k)=
(aj+bjjω1ΔT)cos(jω1k)+
(bj-ajjω1ΔT)sin(jω1k).
(15)

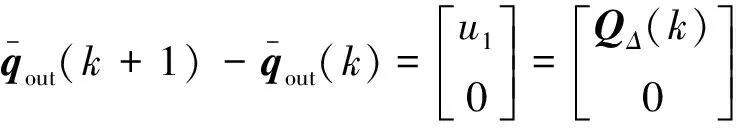
(16)
此处:

ajjω1ΔTsin(jω1(k))].

1.将白菜切成宽约2厘米的条,海带用开水焯透,切成约1厘米的条。猪肉切成片备用,胡萝卜切成片备用,虾皮准备好。

(17)
QLFE(k)的量级远大于QΔ(k),故有

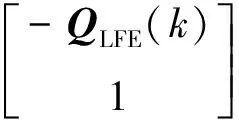
(18)
则


ajjω1sin(jω1k)].
(19)


(20)
式中:

T11=1+(q1)2-(q2)2-(q3)2;
T12=2q3+2q1q2;
T13=-2q2+2q1q3;
T21=-2q3+2q1q2;
T22=1-(q1)2+(q2)2-(q3)2;
T23=2q1+2q2q3;
T31=2q2+2q1q3;
T32=-2q1+2q2q3;
T33=1-(q1)2-(q2)2+(q3)2.
设轨道为圆轨道,则ωoi(k)=[0 -ωoi0]T,则有


(21)
综上,将式(19)、(21)代入式(11),可得

(22)
式中:
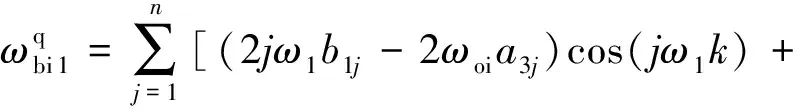
(-2jω1a1j-2ωoib3j)sin(jω1k)];

2jω1a2jsin(jω1k)]-ωoi;
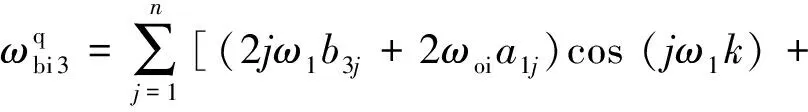
(-2jω1a3j+2ωoib1j)sin(jω1k)].
将式(6)、(22)代入式(8),可得

(23)
式中:

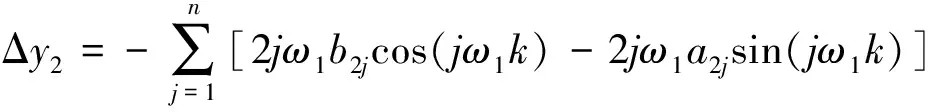

(-2jω1a3j+2ωoib1j)sin(jω1k)].
设经EKF滤波后得的常值漂移中的周期性分量为
Δyb=

(24)

由式(8)应有-Δy=Δyb,令对应项相等,矩阵形式为
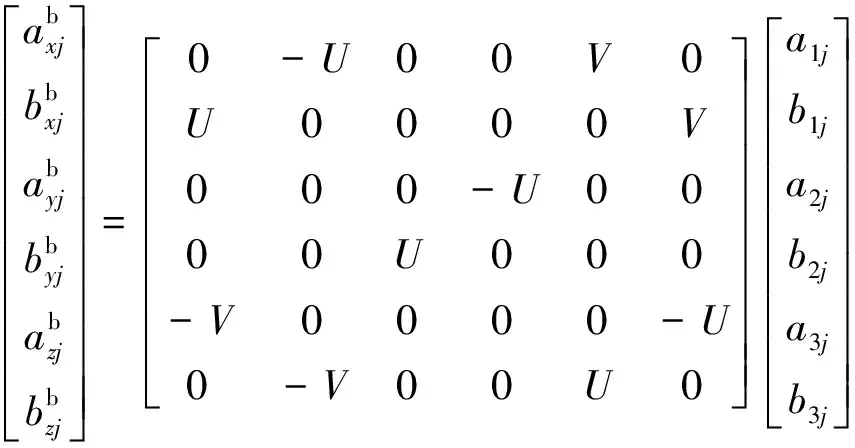
(25)
式中:U=2jω1;V=2ωoi。
2 星敏慢变误差辨识过程
根据常值漂移辨识和补偿星敏感器慢变误差的流程为:
a)对估得的常值漂移进行快速傅里叶变换(FFT),得到慢变误差的基频ω1,j的值;



b0(k)= Δyb=

(26)
再由FFT变换可得ω1,j的各个取值。最后,对每个j及b0的分量分别用最小二乘法求解。对某个确定的j0以及b0的第i个分量(i=x,y,z),有
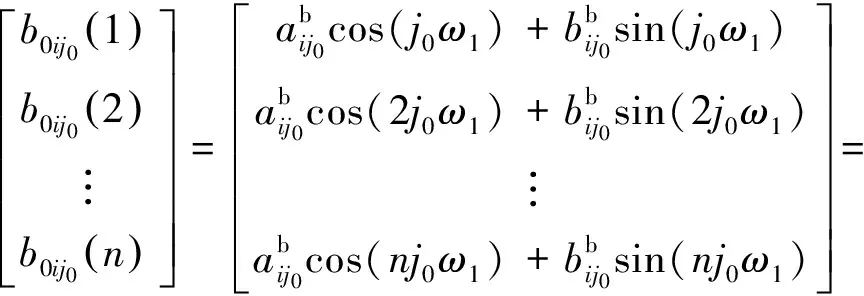

(27)
根据最小二乘法有
x= (ΦTΦ)-1ΦT×
bi0j0(1) bi0j0(2) … bi0j0(n)T.
(28)
仿真中,设置慢变误差的角频率为ω1,2ω1,即j0=1,j1=2,则
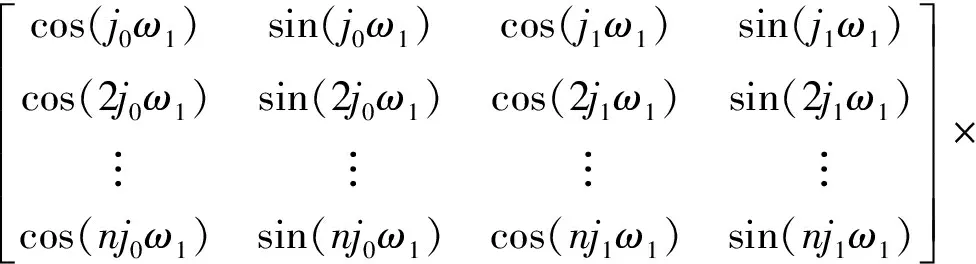

(29)
式中:



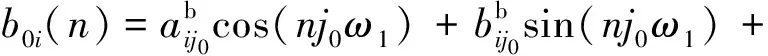
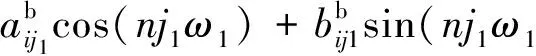
从而求出i向的系数。
说明2:步骤c)中,式(25)中的a2j,b2j与其余分量解耦,总能求出。其余系数a1j,b1j,a3j,b3j,当ω1=ωoi即慢变误差的周期与轨道周期相同时,在j=1时,式(25)的系数矩阵发生奇异,不能求逆,
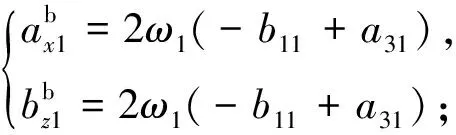
(30)
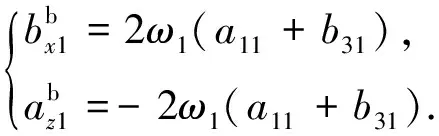
(31)

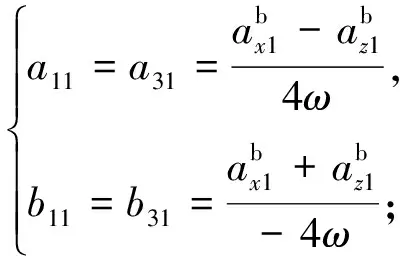
(32)

(33)
3 数值实例
取仿真参数为:陀螺输出只包括常值漂移和绝对误差,不包括随机漂移和随机游走,真值与轨道角速度相同[0 -0.001 103 5 0]Trad/s;星敏感器的误差包括LFE和测量误差,其中LFE
vLFE=VLFEsin(4ω1t)+VLFEcos(2ω1t),
此处:ω1为LFE的基频,与轨道角速度的大小相同(0.001 1 rad/s),VLPE为幅值,为使LFE的影响更显著,取VLFE=100×[6″ 6″ 40″]T;滤波初值,姿态四元数估计为[0 0 0 1]T,陀螺常值漂移为[10 10 10]T(°)/h。姿态角和陀螺的常值漂移的估计结果分别如图1、2所示。
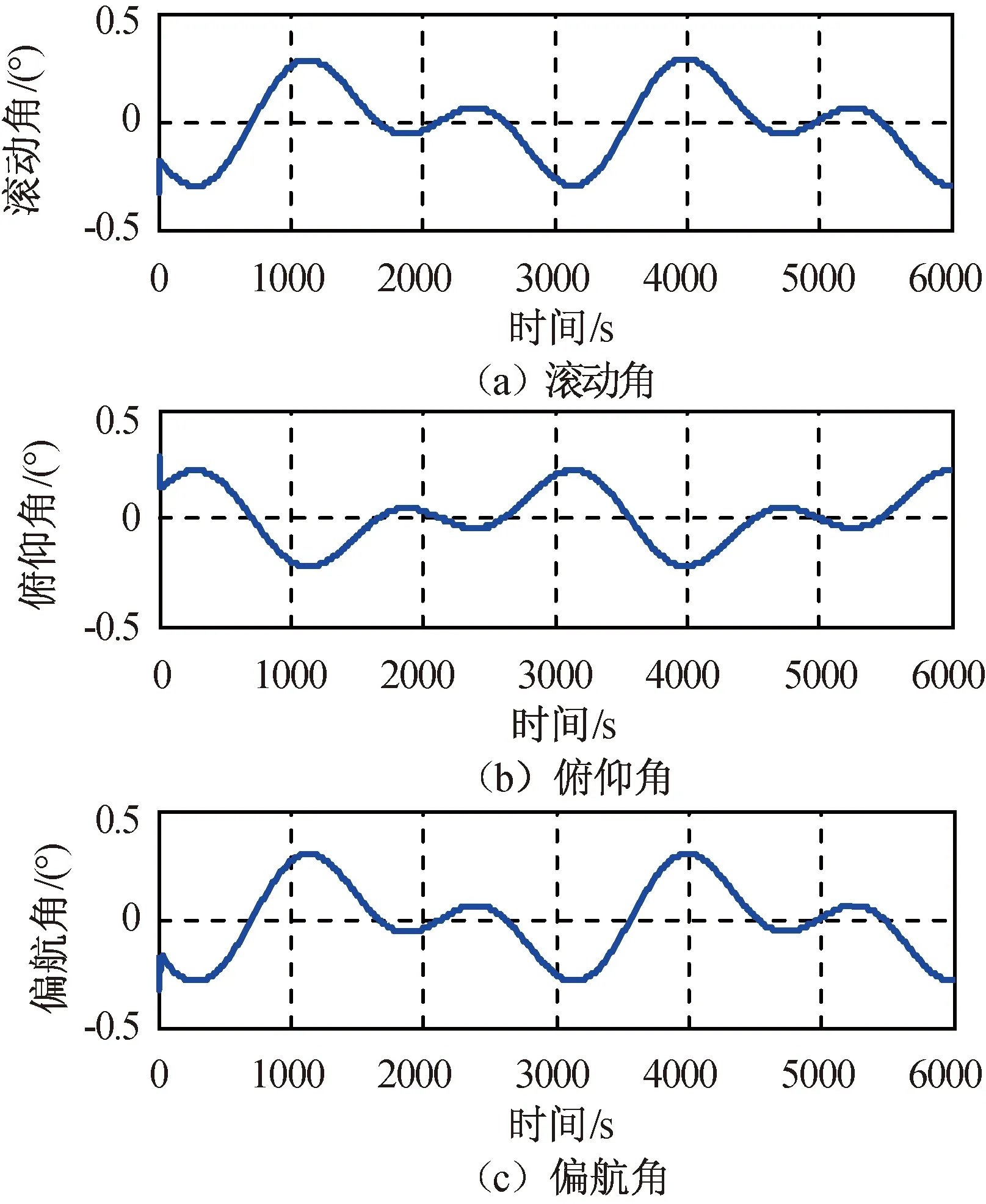
图1 姿态估计结果Fig.1 Estimated attitude angle

图2 常值漂移估计结果Fig.2 Estimated constant drift of gyro
由图1可知:卡尔曼滤波不能消除慢变误差的影响,姿态估计存在周期性变化,且由于慢变误差扩大为原来的100倍,使姿态估计精度下降,滚转和偏航向的姿态估计精度为0.5°,俯仰向的估计精度为0.5°,这是因为星敏感器的光轴与卫星的俯仰轴平行,故俯仰方向的精度相对其他两轴较低。由图2可知:慢变误差导致常值漂移的估计也出现了周期性变化规律。
对常值漂移的估计进行FFT变换,所得频谱如图3所示。由图3可知:经FFT变换后可求出常值漂移的估计中包含主要频率2个,4ωoi,2ωoi与慢变误差中4ωoi及2ωoi对应,这与姿态确定不改变慢变误差所致周期性误差的频率一致。
已知估计常值漂移包含的频率后,用最小二乘法估计幅值,结果见表1、2。由矩阵求逆,求解4ωoi,2ωoi对应的幅值,所得慢变误差的幅值如图4、5所示。
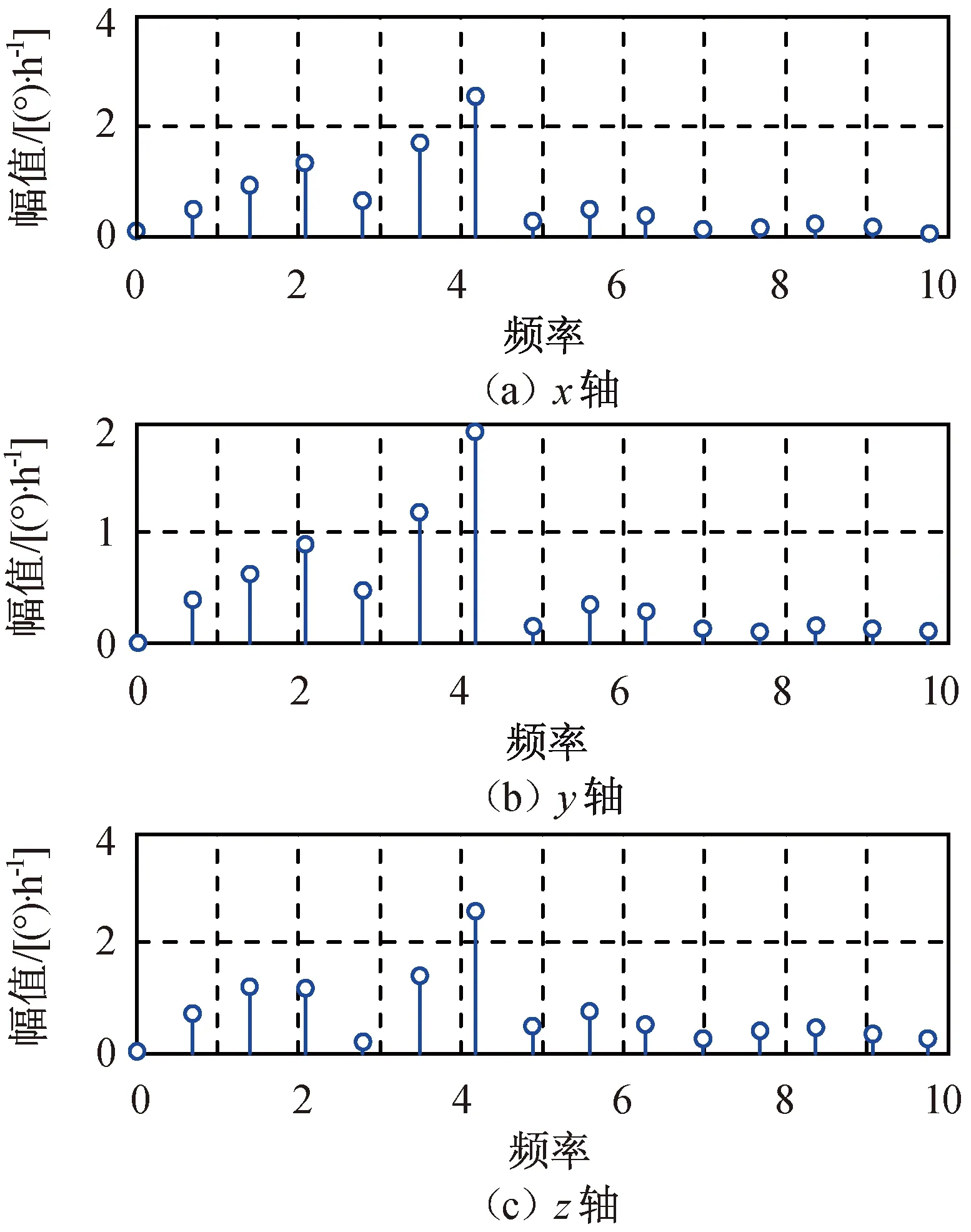
图3 估计常值漂移频谱Fig.3 Spectrum of estimated constant drift of gyro

图4 补偿后的姿态估计结果Fig.4 Estimated attitude angle after compensation

图5 补偿后的常值漂移估计结果Fig.5 Estimated constant drift of gyro after compensation
比较图1、4可知:补偿慢变误差后的姿态估计精度显著提高,其中x、y向的姿态估计精度为0.05°,z向的姿态估计精度为0.1°,较补偿前的姿态精度提高10倍,但由于慢变误差的参数辨识不能完全准确,故姿态估计结果仍存在周期性的变化。
比较图2、5可知:常值漂移估计的准确度也有显著提高,周期性变化的规律不明显。
4 结束语
对高精度姿态确定要求,星敏感器因本身及星上安装支架等结构热变形,导致敏感器输出信息中包含相应的LFE,影响姿态确定结果。本文针对星敏感器LFE影响卫星姿态确定精度的问题,根据理论分析得出的LFE产生机理,用傅里叶级数对LFE建模;基于最小二乘算法,用陀螺的常值漂移特性估计LFE的参数,辨识出傅里叶级数中各正弦函数的振幅;根据傅里叶级数形式的慢变误差模型和估得的慢变误差参数,反演出星体理论上的理想姿态时星敏感器的可能输出,并进行补偿,从而减小慢变误差对姿态确定结果的影响。数学仿真结果表明:本文提出的星敏感器慢变误差标定方法能显著减小低频误差对姿态确定的影响,改善卫星姿态确定精度。与前人方法相比,本文方法的优势是计算量小,原理直观,更易于在轨实现,相关分析结果可为低频误差校准方法的设计和选用提供参考。

表1 常值漂移周期量参数估计结果

表2 估计星敏感器输出周期量幅值
[1] 边志强, 蔡陈生, 吕旺, 等. 遥感卫星高精度稳定度控制技术[J]. 上海航天, 2014, 31(3): 24-33+38.
[2] CRASSIDIS J L, MARKLEY F L, CHENG Y. Survey of nonlinear attitude estimation methods[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(1): 12-28.
[3] HASHMALL J A, NATANSON G, GLICKMAN J, et al. Compensation for time-dependent star tracker thermal deformation on the AQUA spacecraft[R]. Goddard Space Flight Center, 20040171520, 2004.
[4] JORGENSEN J L, DENVER T, BETTO M, et al. The PROBA satellite star tracker performance[J]. Acta Astronautica, 2005, 56: 153-159.
[5] JORGENSEN P S, JORGENSEN J L, DENVER T, et al. In-flight quality and accuracy measurements from the CHAMP advanced stellar compass[J]. Acta Astronautica, 2005, 56: 181-186.
[6] IWATA T, HOSHINO H, YOSHIZAWA T, et al. Precision attitude determination for the advanced land observing satellite (ALOS) : design, verification, and on-orbit calibration[R]. AIAA, 2007-6871, 2007.
[7] 熊凯, 宗红, 汤亮. 星敏感器低频误差在轨校准方法研究[J]. 空间控制技术与应用, 2014, 40(3): 8-13.
[8] WINKLER S, WIEDERMANN G, GOCKEL W. High-accuracy on-board attitude estimation for the GMES Sen-timel-2 satellite: concept, design, and first results[R]. AIAA, 2008-7482, 2008.
[9] XIONG K, TANG L, LEI Y J. Multiple model Kalman filter for attitude determination of precision pointing spacecraft[J]. Acta Astronautica, 2011, 68: 843-852.
[10] 熊凯, 汤亮, 刘一武. 基于地标信息的星敏感器低频误差标定方法[J]. 空间控制技术与应用, 2012, 38(3): 11-15.
Study on Calibration Method of Low Frequency Error for Star Sensor
XU Ying1, 2, WU De-an1, 2, WANG Li-cheng1, 2, LIU De-qing1, 2, XIE Ren-yuan1, 2
(1. Shanghai Space Intellective Control Technology Lab, Shanghai 201109, China; 2. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)
The calibration method of low frequency error (LFE) for star sensor was studied in this paper. According to the mechanism that the LFE was caused primarily by periodic thermal distortion in space, the LFE of star sensor was served as the periodic signal which was characterized by Fourier series. The periodic value in the constant drift of the gyro was estimated by least square method. The parameter of the star sensor’s LFE was recognized by the constant drift. The magnitude of sinusoidal and cosine function in the Fourier series of LFE was determined. Based on LFE model presented in Fouries series and LFE parameter estimated, the LFE expression was given which was used to compensate and calibrate the output of the star sensor. The result showed that the accuracy of the attitude estimation and constant drift of the gyro was improved after the sensor LFE was compensated, which would upgrade the performance of the attitude determination system.
Satellite attitude determination; Star sensor; Low frequency error; Periodicity; Space thermal environment; Calibration; Gyro constant drift; Least square method
1006-1630(2016)04-0063-07
2015-09-15;
2015-11-18
徐 樱(1991—),女,硕士生,主要从事卫星姿态确定技术研究。
V448.21
A
10.19328/j.cnki.1006-1630.2016.04.011
