命题模态逻辑S5系统中并行推理方法*

杨 洋，李广力，张桐搏，刘 磊，吕 帅,2,3+

1.吉林大学 计算机科学与技术学院，长春 130012

2.吉林大学 数学学院，长春 130012

3.符号计算与知识工程教育部重点实验室（吉林大学），长春 130012

命题模态逻辑S5系统中并行推理方法*

杨 洋1，李广力1，张桐搏1，刘 磊1，吕 帅1,2,3+

1.吉林大学 计算机科学与技术学院，长春 130012

2.吉林大学 数学学院，长春 130012

3.符号计算与知识工程教育部重点实验室（吉林大学），长春 130012

YANG Yang,LI Guangli,ZHANG Tongbo,et al.Parallel reasoning methods in propositional modal logic S5. Journal of Frontiers of Computer Science and Technology,2016,10(12)：1783-1792.

S5系统是一类知识表示能力和处理能力都较强的模态公理系统，它是认知逻辑、信念逻辑等非经典逻辑理论的基础。根据Kripke语义模型以及S5系统中部分公理，对命题模态逻辑S5公理系统的性质进行了较为深入的研究，并对S5系统中一类具有代表性的标准模态子句集的特性进行了分析，提出了一种基于扩展规则方法的命题模态逻辑推理算法（propositional modal clausal reasoning based on novel extension rule，PMCRNER）。针对朴素算法时间复杂度较高的问题，利用任务间潜在的关联性对算法同时进行了粗粒度与细粒度并行化，提出了并行算法PPMCRNER（parallel PMCRNER）理论框架，并且与基本算法进行了对比。实验结果表明，PPMCRNER算法在不可满足的子句集上的推理具有良好的加速比，为高时间复杂性的模态推理方法的进一步研究提供了一种可行方案。

命题模态逻辑；S5公理系统；并行推理；扩展规则

1 引言

近年来，多种以模态逻辑为基础的复杂公理系统与框架被相继提出[1-3]，关于模态逻辑甚至是更高阶的逻辑知识表示形式的理论研究逐渐成为人们关注的热点[4]。模态逻辑推理方法的研究是高阶公理系统和框架的原型实现的基础。自动推理领域主流的推理方法为归结方法、表推演方法和扩展规则推理方法。推理的公式集一般为非CNF（conjunctive normal form）和CNF公式。结合基础推理方法，命题模态逻辑的推理方法有直接推理和转换推理两种。鉴于不同模态系统中的公理存在着较大差异，因此现阶段主流模态推理方法和证明系统大部分都是基于具体的模态公理系统或者模态语言。

2006年，Wu等人提出了一种在命题模态逻辑K系统中的破坏性扩展规则推理方法[5]，并且将扩展规则推理过程和化简过程交替进行，加速算法的求解过程。该方法保留了扩展规则求解问题的优势，对于互补因子率较高的模态公式能够快速地进行可满足性判定。同年，Schmidt探讨了命题动态模态逻辑不同推理方法的发展，阐明了表推演系统、归结系统、双重表推演系统中如何通过一些规则使其能够扩展到一阶命题逻辑[6]。2007年，Nalon等人提出了一种正规模态逻辑中基于归结的推理方法，通过一组公理来对模态逻辑公式进行直接推理，同时为许多正规多模态逻辑的推理方法给出了正确性和完备性的结果[7]。2008年，吴瑕等人提出了一种命题模态逻辑中关系扩展规则推理方法[8]。其主要思想是使用关系转换函数对Kripke语义模型进行转换，使用一阶扩展规则方法对转换后的结果进行推理。2013年，Benzmüller等人提出了一种使用高阶逻辑定理证明器来求解一阶模态逻辑可满足性问题的方法，并且给出了一阶模态逻辑（first-order modal logic，FML）到高阶逻辑（high-order logic，HOL）的转换工具[9]。近年来，由于SAT（satisfiability）比赛的推广以及命题逻辑SAT求解器求解效率的大幅提升，更多的学者开始寻求转换方法来将多种不同的模态公理系统转化为命题SAT求解。2013年，Kaminski等人通过一组公理转换规则将模态可满足性问题转化成普通的布尔可满足性问题，调用命题SAT求解器进行求解，得到了较好的效果[10]。2014年，Rajeev等人提出了一种使用二元决策图（binary decision diagrams，BDDs）替换DPLL的算法求解模式来求解模态可满足性问题，通过与多个求解器进行对比展现了其优越的求解能力[11]。

2 基础知识

2.1 扩展规则

扩展规则方法的原理为给定命题变量集上的所有极大项之间的合取是不可满足的。扩展规则[12]的定义为：给定一个子句C和不在C中出现的原子a，D={C∨a，C∨¬a}，称由C到D的推导过程为扩展规则，D为子句C关于原子a应用扩展规则的结果。显然，公式集D在真值指派上和公式集C逻辑等价。因此，可以对子句集中的任意子句应用类似上述的推导过程，逐步扩展成只包含形式为极大项的子句集。朴素扩展规则算法（extension rule，ER）的基本思想是：搜索所有的极大项空间，若待判定的子句集能够扩展出所有的极大项空间，则该子句集不可满足；否则该子句集可满足。

在2009年李莹等人提出的基于扩展规则的NER（novel extension rule）推理方法中[13]，其进行逆向推理，不断取给定命题变量集上的极大项依次判断能否被指定子句集扩展出来，以此来获得公式是否可满足的结论。在该方法中，其避免了朴素扩展规则ER繁重的容斥原理求解过程和内存溢出问题，以时间效率换取空间开销，是一种较优的推理方法。本文将借助NER推理方法来进行模态公式推理。

目前，扩展规则的应用研究还仅限于起步阶段，其研究成果主要包括命题逻辑知识编译、搜索方法的启发式策略、可能性推理与知识编译、模型计数以及#SAT问题求解等[14-19]。而对于高阶逻辑的推理方法的应用研究还处于空白阶段。

2.2 命题模态系统

命题模态逻辑公理系统在命题逻辑系统的基础上进行了扩展，在保持系统推理结构封闭的情况下加入了部分公理和规则。公理系统分为正规系统和非正规系统，通常对模态逻辑的正规系统进行推理。常用的模态逻辑正规系统主要有K、T、D、S4、S5、B等系统。K系统为命题模态逻辑中最小的正规系统，它相比于经典命题逻辑系统增加了K公理(□(P→Q)→(□P→□Q))和必然化规则（如果⊦KP，则⊦K□P）。而其他系统分别在K系统的基础上添加了相应的公理，使得相应的公理系统增加了不同的约束和性质。需要强调的是：S5系统是在T系统的基础上添加了E公理而形成的[20]。命题模态逻辑推理是在特定的公理系统中对一组任意的命题模态公式进行可满足性判断的过程。命题模态逻辑推理的过程比命题逻辑推理更复杂，因为在对模态公式进行推理时不仅要考虑命题变量集的真值指派，还要考虑必然和可能算子导致的命题公式在Kripke可能世界模型中的世界转移，所以如何对模态算子的处理是命题模态逻辑推理过程的核心，对于命题的部分，只需要考虑使用常规命题逻辑的推理方法即可。命题模态逻辑S5公理系统是一种有代表性的公理系统，它也是认知逻辑和信念逻辑的基础。在S5系统中，可以只保留一个模态算子，即必然算子□。在不同的逻辑中，该算子代表的含义也不尽相同。如在认知逻辑中，该算子代表某智能体知道某个事件；而在信念逻辑中，该算子代表某个智能体相信某个事件。因此，研究该系统的推理方法对于更高级的认知逻辑、信念逻辑和道义逻辑等推理方法的研究有着重要意义。

需要指出的是，目前命题模态逻辑的推理方法研究还处于理论阶段，并且大多数对于该逻辑的研究主要集中在K、T公理系统中，对于多约束的公理系统的通用形式化推理算法还较少，本文将对S5系统的推理方法进行研究，并进行一系列相关实验。

3 命题模态逻辑S5系统中标准模态子句集推理方法

3.1 定义与引理

模态逻辑S5公理系统在T系统的基础上增加了E公理（◇P→□◇P），利用该公理，对于系统中的模态公式可以进行模态度归约，使得任意公式能够归约为模态度小于等于1的模态公式，并且通过化简等手段将模态公式转化为标准模态子句集或者标准模态子句块。

下面给出标准模态子句的定义：

标准模态子句：令ФP为模态文字，其中Ф是有限个必然与可能算子的序列，并且该序列可以为空串，P为命题文字。若干个模态文字的析取式为标准模态子句。

S5系统具有对称性，不能使用破坏性方法对其进行推理，因此可以通过间接转化的方法对其进行推理，其中最重要的转化规则为分裂规则和归约规则。

分裂规则[5]：如果一个子句集包含一个至少包含两个模态文字的子句C，那么该子句集可以由两个子句集来替代，其中一个子句集是原子句集中非C子句集与子句C中的一个模态文字的合取，另一个子句集是原子句集中非C子句集与子句C中的其余子句的合取。

归约规则：因为S5系统是S4系统的扩张，那么借助S4系统中与S5系统中□P↔□□P，◇P↔◇◇P，◇P↔□◇P，□P↔◇□P这4条定理，可以对任意长度的模态算子序列，删去前面的任意长度而只保留最里层的模态算子。

因为K系统是最小的正规模态系统，所以K系统中的任意定理在S5系统中都适用，K系统中的定理(◇P∨◇Q↔◇(P∨Q))可以应用于S5系统中，对在一个标准模态子句中具有相同可能算子前缀的模态文字进行合并，便于后续处理。

单模态单元子句：令ФQ为单模态单元子句，其中Ф是单个必然算子或者单个可能算子或者为空，Q为命题逻辑中的标准子句。由单模态单元子句组成的子句集叫作单模态单元子句集。

3.2 基于NER的命题模态子句推理算法

基于上述的规则和定义，命题模态逻辑S5系统中子句形式的推理算法的核心思想如下：

（1）预处理

对于初始输入的标准模态子句集，使用归约规则对含有超过一个模态算子序列的模态文字进行归约，使得算法真正处理的输入为所有模态文字均不含有超过一个模态算子的标准模态子句集，该操作能够在线性时间复杂度内完成。

（2）合并

扫描经过预处理的标准模态子句集，对子句中出现的形如◇P∨◇Q析取式进行合并。注意，形如□P∨□Q的公式无法进行合并，因为合并后的形式与原形式不保持Kripke语义等价，只合并可能算子。该操作同样能够在线性时间复杂度内完成。

（3）拆分

任意选取经过合并操作后的子句集中的非单模态单元子句，使用分裂规则对子句集进行拆分，形成两个子句列表，子句列表之间的可满足性为析取关系。

（4）可满足性判定

在拆分过程中，可以边拆分边判断，判断的形式是拆分的子句列表出现单模态单元子句集。调用可满足性判定算法（在后文详述）。如果一个子句列表判定为可满足，则结束全部的拆分和求解过程，返回可满足；否则只有当所有子句列表都返回不可满足时，算法结束。

单模态单元子句集的可满足性判定：

输入参数为单模态单元子句集时，考虑到多模态算子公式已经被归约为单模态算子，则在处理单模态算子时只需要考虑一层的世界转移即可，即判断当前世界以及当前世界的后继世界即可，不需要再考虑后继的后继或者更多，因此在处理过程中只需要将子句集转化成命题形式即可。

对于命题子句集，不仅需要考虑当前世界的可满足性，还得考虑其对后继世界的可满足性影响。因为S5系统是在T公理系统之上的模态逻辑公理系统，则T公理系统中的约束对于S5系统同样成立。在T公理系统中，有公理P→◇P，则在处理单模态单元子句集时，需要将每一个出现的命题子句进行复制，并且对复制后的每一个子句最外层附加一个可能算子，将这样的公式加入原单模态单元子句集中进行求解。对于带模态算子的子句，优先考虑带必然算子的单模态单元子句，当前世界的后继世界的个数为命题变量个数的2的幂次方。在可满足性判定时，首先使用该子句列表中的所有带必然算子的单模态单元子句依次对这些不可满足的后继可能世界进行“杀死”操作，进行完一轮后，剩余的可能世界集为满足所有带必然算子中的命题公式。然后将带可能算子的单模态单元子句的命题部分传递到剩余世界判定，如果存在一个世界能够使得该子句的命题部分为真，则判断结束，依次判断所有带可能算子的单模态单元子句。

开始使用带必然算子的单模态单元子句集“杀死”任意一个使其命题部分为假的世界实际上是对于该部分子句集的命题部分，寻找是否有解，能够使得带必然算子的单模态单元子句的命题部分全部为真。接下来使用带可能算子的单模态单元子句的命题部分在剩下的世界里寻找是否存在能够使其为真的世界，是将每一个带可能算子的单模态单元子句的命题部分加入带必然算子的单模态单元子句集的命题部分寻找该整体命题子句集是否有解。最后对命题部分的求解，同样是受限于T公理的约束，在T公理系统中，有公理（□P→P）。因此，必须将该子句列表中的所有带必然算子的单模态单元子句的命题部分进行剥落，然后将其添加到该子句列表的命题公式部分，统一进行可满足性判定。

因此本文在处理过程中将带必然算子的单模态单元子句集的命题部分单独判定其可满足性，然后依次把带可能算子的单模态单元子句的命题部分加入到带必然算子的单模态单元子句集的命题子句集中，判定其可满足性，只要存在一个使其不可满足，则整体不可满足，只有每一个带可能算子的单模态单元子句判定均可满足，则整体才可满足。

例 F={□◇□A∨◇◇B,□¬A∨◇¬B∨C}，对该公式的推理步骤如下：

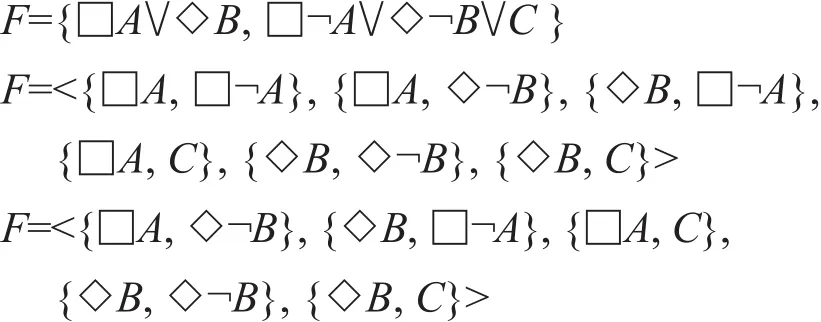
返回SAT。

综上所述，给出命题模态逻辑S5中的子句形式的推理算法。

算法1 PMCRNER（propositional modal clausal reasoning based on novel extension rule）

算法2 SMRNER（single modal reasoning based on novel extension rule）

算法1中的IsSingle函数是判断当前合取公式是否为单模态单元子句集，如果是，则调用基于NER的单模态单元子句集求解算法SMRNER进行求解，否则继续进行拆分，直到所有单模态单元子句集全部被处理。choose函数是在公式F1中任意选择一个标准模态子句进行拆分。

算法2中的GetP函数的功能为得到当前子句列表中的命题部分；AddPO函数的功能为为当前子句列表中的每一个命题子句的最外层添加一个可能算子，将其变成命题模态子句；GetNO函数的功能为得到当前子句列表中所有带必然算子的子句的命题部分；GetPO函数的功能为得到当前子句列表中所有带可能算子的子句的命题部分。

显然，该算法对于命题模态逻辑S5公理系统中的子句形式推理是正确并且完备的。

3.3 PPMCRNER算法

上节给出了PMCRNER算法，但朴素版本的算法时间复杂度较高，需要寻找新的方法使得算法的执行效率得到提高，在进行可满足性判定时能够提前结束。本节将该形式的推理算法进行了并行化，在特定的子句集上得到了较好的加速效果。

3.3.1 粗粒度并行

上节中，将标准模态子句拆分成不同的子句列表进行求解，该部分在串行算法中是顺序执行的。可以将该部分执行过程并行化，得到粗粒度并行的目的。

3.3.2 细粒度并行

也可以考虑将子句列表的可满足性判定过程并行化。在对子句列表运用T系统中的两条公理后，将后继世界之间的可满足性判定和命题逻辑的可满足性判定并行化。由于多个带可能算子的子句均需要同所有带必然算子的子句进行后继世界可满足性判定，可以将它们的执行过程并行化，同时将命题部分的执行过程同样并行化，达到细粒度并行的目的。

3.3.3PMCRNER算法的并行化

综上所述，当将算法粗粒度和细粒度并行化之后，就得到了全并行的PMCRNER推理算法——PPMCRNER算法。下面给出PPMCRNER算法的理论框架。

在算法执行之前，需要对公式集进行预处理，处理的大致流程如下。

算法3 PPMCRNER(parallel propositional modal clausal reasoning based on novel extension rule)

否则返回第1步.

算法4 PSMRNER（parallel single modal reasoning based on novel extension rule）

在Predeal中，flag变量和Flag[]数组分别为标记变量和标记数组，用于主方法对子方法进行调度控制。在PPMCRNER算法中，Allocate函数的功能为将当前生成的单模态单元子句集（子句列表）按照一定的策略分给某个分方法，用于并行执行。算法中其余符号与PMCRNER算法中的符号含义相同。

4 实验结果与分析

该部分拟采用随机生成的标准模态子句集来对串行、全并行算法的性能进行测试。在进行实验的过程中，发现同样规模的标准模态子句集和命题逻辑子句集，在推理时其时间复杂度已经差了好几个数量级。因此，为了实验能够产生令人接受的有效结果，在随机生成标准模态子句集时将标准模态子句中的必然算子的个数限制在3个以内，而可能算子的个数与命题原子的个数不作限制。本文分别在可满足的标准模态子句集和不可满足的标准模态子句集上进行了大量的测试，随机样例有两个参数＜N, K＞，其中N代表子句集中变量的个数，K代表子句的个数。实验环境：Windows 8操作系统，i7-3770 CPU，8 GB RAM。

4.1 不可满足子句集

本组对比实验中，选取命题变量数为10，模态算子数任意的不可满足标准模态子句集进行测试，结果如图1所示。其中，图（a）为串行算法和全并行算法的时间对比图，横轴为子句数，纵轴为CPU时间。图（b）为全并行算法相对于串行算法的加速比。很明显，随着子句数的不断增加，加速比呈不断上升趋势并且接近于3。

本组对比实验中将命题变量数改为15，其余条件和设定同上组实验一样，结果如图2所示。可以看出，该组对比实验呈现出了与上组实验相同的效果和趋势。可以认为，该算法对于不同规模的测试样例是具有稳定性的。

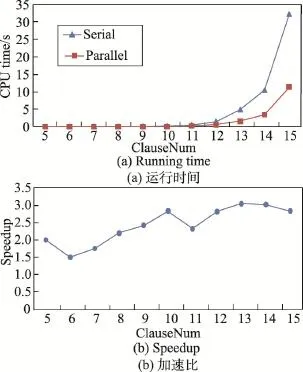
Fig.1 Experimental results of random problem＜10,K＞instances on unsatisfiable clause sets图1 不可满足子句集上随机问题＜10,K＞用例测试结果

4.2 可满足子句集

本组对比实验里选取命题变量数为10，模态算子数任意的可满足标准模态子句集进行测试，结果如图3所示。其中，图（a）为串行算法和全并行算法的时间对比图，横轴为子句数，纵轴为CPU时间。图（b）为全并行算法相对于串行算法的加速比。可以看出，在测试数据为可满足子句集的情况下，串行算法和全并行算法的效率差距不大，且略高于全并行算法。

同样的，对于可满足的标准模态子句集，增加测试数据的规模，将命题变量数增加到15，结果如图4所示。可以看出，即使测试数据的规模增加，算法的对比结果仍然保持同样的趋势。算法对于可满足的不同规模的测试数据是具有稳定性的。

Fig.2 Experimental results of random problem＜15,K＞instances on unsatisfiable clause sets图2 不可满足子句集上随机问题＜15,K＞用例测试结果

4.3 分析

本文对大量数据集进行了测试，分析结果如下：

（1）此类测试数据集具有代表性的通用benchmark较少，故采用随机生成的策略来产生数据集。大量测试表明，随机生成可满足的标准模态子句集更容易。

（2）模态公式的推理时间复杂度远远超过了同规模的命题公式，子句个数一旦过大，推理的时间复杂度将以指数级别的增长趋势达到让人难以接受的程度。

（3）从大量测试数据来看，并行算法具有一定的适用性。事实上，并行算法并不是在所有的标准模态子句集上都比串行快，相反的，在某些特定的子句集上其性能略低于串行算法。在可满足的标准模态子句集上，并行算法的执行效率反而比串行算法慢。原因在于对可满足的标准模态子句集进行推理的时候，大部分子句集在拆分子句列表的时候其中前一部分子句列表集合中就已经出现可满足的子句列表，那么并行算法的粗粒度并行并没有得到真正执行。相反的，并行算法真正实现的时候其复杂的线程之间的调度与通信往往是一笔不小的开销，执行效率反而有所降低。

（4）并行算法对于不可满足的标准模态子句集具有稳定的加速比，但无论分多少个任务并行，真正的加速比还是受限于CPU物理内核的个数，其加速比能够接近CPU物理内核的个数。

（5）实验表明，细粒度并行策略的加速比并不显著。在实验中，尝试分别将粗粒度并行与细粒度并行进行分开实验。事实上，全并行算法的加速比和只有粗粒度并行的版本相比，其加速程度并没有明显提高。细粒度并行的加速程度主要受限于单模态单元子句集中可能算子的个数，同时在粗粒度与细粒度同时并行的时候，其融合后的加速比受限于物理硬件。

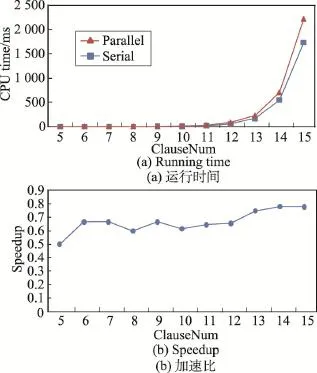
Fig.3 Experimental results of random problem＜10,K＞instances on satisfiable clause sets图3 可满足子句集上随机问题＜10,K＞用例测试结果

Fig.4 Experimental results of random problem＜15,K＞instances on satisfiable clause sets图4 可满足子句集上随机问题＜15,K＞用例测试结果

5 结论与展望

本文提出了命题模态逻辑S5系统中一种新的基于扩展规则的标准模态子句集的串行推理算法和并行推理算法，并对其进行了大量的对比测试。实验表明，PPMCRNER算法具有一定的适用性，在不可满足的子句集中具有稳定的加速比，在可满足的子句集中加速效果并不明显。

完备算法的时间复杂度较高，原因在于一旦标准模态子句中必然算子的个数增加，则整个子句集的推理时间复杂度的增加程度是难以接受的。此外完备算法中应用规则时，标准模态子句中只有可能算子间的文字能够进行合并，而必然算子间却不允许，原因在于◇P∨◇Q↔◇(P∨Q)成立，而□P∨□Q↔□(P∨Q)却不成立。因此可以在实际推理时先运行一个不完备的算法，思想是加强完备算法中的归约规则，加入一条定理□P∨□Q→□(P∨Q)。运用此定理合并标准模态子句中的所有必然算子，将所有的标准模态子句全部变成最多只有一个必然算子和一个可能算子的子句，这样推理的时间复杂度会大大降低。如果不完备算法返回不可满足，则原公式也不可满足；若不完备算法返回可满足，则需要重新调用完备的算法来进行推理。

可以进一步研究并行算法的粗粒度并行策略，使得其对于可满足的标准模态子句集也同样具有稳定的加速比。该问题的关键在于采用何种子句列表拆分策略使得各分线程在能够“均匀”地处理子句列表的同时，线程之间的同步与通信的开销不至于过大，这样可以使得算法的加速性能得到进一步提升。

[1]Meghdad G.Distributed knowledge justification logics[J]. Theory of Computing Systems,2014,55(1):1-40.

[2]Zadeh L A.A note on modal logic and possibility theory[J]. Information Sciences,2014,279:908-913.

[3]Larsen K G,Mardare R.Complete proof systems for weighted modal logic[J].Theoretical Computer Science,2014,546: 164-175.

[4]French T,van der Hoek W,Iliev P,et al.On the succinctness of some modal logics[J].Artificial Intelligence,2013, 197:56-85.

[5]Wu Xia,Sun Jigui.Destructive extension rule in proposition modal logic K[C]//Proceedings of the 1st International Conference on Computational Methods,Singapore,Dec 15-17,2004:1087-1091.

[6]Schmidt R A.Developing modal tableaux and resolution methods via first-order resolution[C]//Proceedings of the 6th Conference on Advances in Modal Logic,Noosa,Australia,Sep 25-28,2006,6:1-26.

[7]Nalon C,Dixon C.Clausal resolution for normal modal logics[J].Journal ofAlgorithms,2007,62(3):117-134.

[8]Wu Xia,Yu Haihong,Li Zehai,et al.Relational extension rule[J].Journal of Jilin University:Science Edition,2008, 46(3):504-508.

[9]Benzmüller C,Raths T.HOL based first-order modal logic provers[C]//LNCS 8312:Proceedings of the 19th International Conference on Logic for Programming,Artificial Intelligence,and Reasoning,Stellenbosch,South Africa, Dec 14-19,2013.Berlin,Heidelberg:Springer,2013:127-136.

[10]Kaminski M,Tebbi T.InKreSAT:modal reasoning via incremental reduction to SAT[C]//LNCS 7898:Proceedings of the 24th International Conference on Automated Deduction,Lake Placid,USA,Jun 9-14,2013.Berlin,Heidelberg: Springer,2013:436-442.

[11]Rajeev G,Kerry O,Jimmy T.Implementing tableau calculi using BDDs:BDDTab system description[C]//LNCS 8562: Proceedings of the 7th International Joint Conference on Automated Reasoning,Vienna,Austria,Jul 19-22,2014.Berlin,Heidelberg:Springer,2014:337-343.

[12]Lin Hai,Sun Jigui,Zhang Yimin.Theorem proving based on the extension rule[J].Journal of Automated Reasoning, 2003,31(1):11-21.

[13]Sun Jigui,Li Ying,Zhu Xingjun,et al.A novel theorem proving algorithm based on extension rule[J].Journal of Computer Research and Development,2009,46(1):9-14.

[14]Lin Hai,Sun Jigui.Knowledge compilation using the extension rule[J].Journal of Automated Reasoning,2004,32(2): 93-102.

[15]Li Ying,Sun Jigui,Wu Xia,et al.Extension rule algorithms based on IMOM and IBOHM heuristics strategies[J].Journal of Software,2009,20(6):1521-1527.

[16]Lai Yong,Ouyang Dantong,Cai Dunbo,et al.Model counting and planning using extension rule[J].Journal of Computer Research and Development,2009,46(3):459-469.

[17]Yin Minghao,Lin Hai,Sun Jigui.Solving#SAT using extension rules[J].Journal of Software,2009,20(7):1714-1725.

[18]Yin Minghao,Sun Jigui,Lin Hai,et al.Possibilistic extension rules for reasoning and knowledge compilation[J]. Journal of Software,2010,20(11):2826-2837.

[19]Liu Lei,Niu Dangdang,Lv Shuai.Knowledge compilation methods based on the hyper extension rule[J].Chinese Journal of Computers,2016,39(8):1681-1696.

[20]Zhou Beihai.Introduction to modal logic[M].Beijing:Peking University Press,1997.

附中文参考文献：

[8]吴瑕,于海鸿,李泽海,等.关系扩展规则[J].吉林大学学报:理学版,2008,46(3):504-508.

[13]孙吉贵,李莹,朱兴军,等.一种新的基于扩展规则的定理证明算法[J].计算机研究与发展,2009,46(1):9-14.

[15]李莹,孙吉贵,吴瑕,等.基于IMOM和IBOHM启发式策略的扩展规则算法[J].软件学报,2009,20(6):1521-1527.

[16]赖永,欧阳丹彤,蔡敦波,等.基于扩展规则的模型计数与智能规划方法[J].计算机研究与发展,2009,46(3):459-469.

[17]殷明浩，林海，孙吉贵.一种基于扩展规则的#SAT求解系统[J].软件学报,2009,20(7):1714-1725.

[18]殷明浩，孙吉贵，林海,等.可能性扩展规则的推理和知识编译[J].软件学报,2010,21(11):2826-2837.

[19]刘磊,牛当当,吕帅.基于超扩展规则的知识编译方法[J].计算机学报,2016,39(8):1681-1696.

[20]周北海.模态逻辑导论[M].北京:北京大学出版社,1997.

YANG Yang was born in 1992.He is an M.S.candidate at Jilin University.His research interests include intelligent planning,automated reasoning and cloud computing,etc.

杨洋（1992—），男，吉林大学硕士研究生，主要研究领域为智能规划，自动推理，云计算等。

LI Guangli was born in 1992.He is an M.S.candidate at Jilin University.His research interests include automated reasoning,cloud computing and parallel programming,etc.

李广力（1992—），男，吉林大学硕士研究生，主要研究领域为自动推理，云计算，并行编程等。

ZHANG Tongbo was born in 1995.He is a student at Jilin University.His research interests include automated reasoning,cloud computing and parallel programming,etc.

张桐搏（1995—），男，吉林大学学生，主要研究领域为自动推理，云计算，并行编程等。

LIU Lei was born in 1960.He received the M.S.degree in computer software from Jilin University in 1985.Now he is a professor and Ph.D.supervisor at Jilin University.His research interest is software theory and technology.

刘磊（1960—），男，吉林长春人，吉林大学教授、博士生导师，主要研究领域为软件理论与技术。累计发表学术论文180余篇，主持国家自然科学基金等科研项目30余项。

LV Shuai was born in 1981.He received the Ph.D.degree in computer software and theory from Jilin University in 2010.Now he is an associate professor at Jilin University.His research interests include intelligent planning and automated reasoning,etc.

吕帅（1981—），男，吉林公主岭人，2010年于吉林大学获得博士学位，现为吉林大学副教授，主要研究领域为智能规划，自动推理等。累计发表学术论文61篇，主持国家自然科学基金等科研项目7项，获得全国商业科技进步一等奖2项、吉林省科学技术进步三等奖2项。

Parallel Reasoning Methods in Propositional Modal Logic S5*

YANG Yang1,LI Guangli1,ZHANG Tongbo1,LIU Lei1,LV Shuai1,2,3+
1.College of Computer Science and Technology,Jilin University,Changchun 130012,China
2.College of Mathematics,Jilin University,Changchun 130012,China
3.Key Laboratory of Symbolic Computation and Knowledge Engineering(Jilin University),Ministry of Education, Changchun 130012,China
+Corresponding author:E-mail:lus@jlu.edu.cn

S5 system is a special and important axiomatic system in propositional modal logic that has great ability of knowledge representation and processing,which is the basis of non-classical logics such as epistemic logic and belief logic etc.According to Kripke semantic model and part of the axioms in S5 system,this paper gives a more indepth research on the characteristics of propositional modal logic S5,and analyzes the features of a kind of representative formulae which is standard modal clauses,then proposes an NER-based algorithm called PMCRNER(propositional modal clausal reasoning based on novel extension rule)which is used to reason for standard modal clauses in propositional modal logic S5.In the view of high time complexity in simple algorithm,this paper uses the potential relevance between tasks to make the algorithm parallel in the degree of coarse-granularity and fine-granularity.This paper also gives the theoretical framework of PPMCRNER(parallel PMCRNER)and compares it with the basic algorithm.The experiments show that PPMCRNER has good speedup on unsatisfiable clause sets,and provides a feasible scheme for further research on the reasoning methods for modal formulae which are hard to solve.

propositional modal logic;S5 axiom system;parallel reasoning;extension rule

10.3778/j.issn.1673-9418.1509035

A

TP181

*The National Natural Science Foundation of China under Grant Nos.61300049,61502197,61503044(国家自然科学基金);the Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No.20120061120059(高等学校博士学科点专项科研基金).

Received 2015-09,Accepted 2015-11.

CNKI网络优先出版:2015-12-03,http://www.cnki.net/kcms/detail/11.5602.TP.20151203.0826.002.html