生成函数在组合数学中的若干应用*

王中平

(重庆大学 数学与统计学院，重庆 401331)



生成函数在组合数学中的若干应用*

王中平

(重庆大学 数学与统计学院，重庆 401331)

生成函数是组合数学中的一个重要理论工具，它在组合问题中的应用既灵活又具有一定的广泛性，它不仅可以用来推导或者证明各种有用的组合恒等式，还可以用来处理组合计数问题、整数分拆问题、递推关系问题等。本文主要研究了生成函数在以上列举的几个典型的组合数学问题中的一些应用，从中也能体现生成函数这一工具对我们处理组合数学问题的优越性。

生成函数；组合恒等式；组合计数；整数分拆；递推关系

1 生成函数相关介绍

生成函数又叫发生函数或者母函数,它的提出巧妙地将离散数学与连续数学结合起来,为离散数学中特别是当中组合数学的许多问题提供了好的解决办法,成为研究组合数学必不可少的工具之一。生成函数作为一种十分有用的方法，它的运用非常广泛，它处理问题的思想也不复杂,其主要思路就是把离散的序列和相应的幂级数联系起来,通过对幂级数之间的运算，来得到相应的离散序列之间的一些性质及其相互关系等。

实际上，生成函数就是一种形式幂级数，所以有必要先来给出形式幂级数的定义：

定义1.1[1]形式幂级数是指形如

a0+a1x+a2x2+…

的表达式，其中的{an}是系数序列。

这里的形式幂级数的概念实质上是二项式概念的推广，并且当两个形式幂级数的系数全部对应相等时，就说这两个形式幂级数相等。

下面我们给出发生函数的定义：

定义1.2[2]对于给定的实数或复数序列a0,a1,…,an,…,我们称形式幂级数

为这个序列的生成函数，并且一般把这种形式的生成函数称为普通型生成函数。

定义1.3[2]对于给定的实数或复数序列a0,a1,a2,…，an,…,我们称形式幂级数

为序列{an}的指数型生成函数。

有时我们也将序列{an}的生成函数记为G{an}，并且上面定义中的序列{an}通常是由具有某种实际组合意义的正整数构成。下面我们来介绍生成函数的重要运算性质：

定理1.4[3]设{ak},{bk}为两个数列，则

(1)G{ak}±G{bk}=G{ak±bk}；

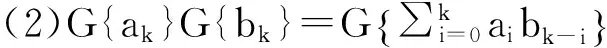
证明：

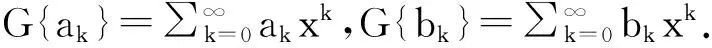
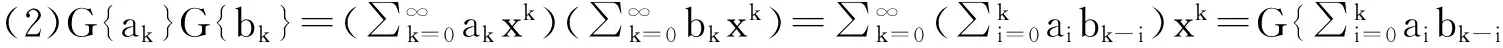
证毕。

一般来说, 普通型的生成函数比较适合处理组合数相关问题,指数型的生成函数比较适用于解决排列数相关问题，所以，我们在选用生成函数解决问题时,要根据所要处理的问题的特点和性质,有方向性地选择某种类型的生成函数，以使问题更好地得到解决。

根据幂级数的性质,只要两个幂级数的收敛半径非零,就可以在某区间内进行加、减、乘、除、求积分、求导等各种运算,而不需要去考虑级数的敛散性。因此,在后面的讨论中,只要在某非零点收敛,我们就不再关心它的收敛域。

运用生成函数处理组合数学问题的一般思路可以简要地概括为如下框图：

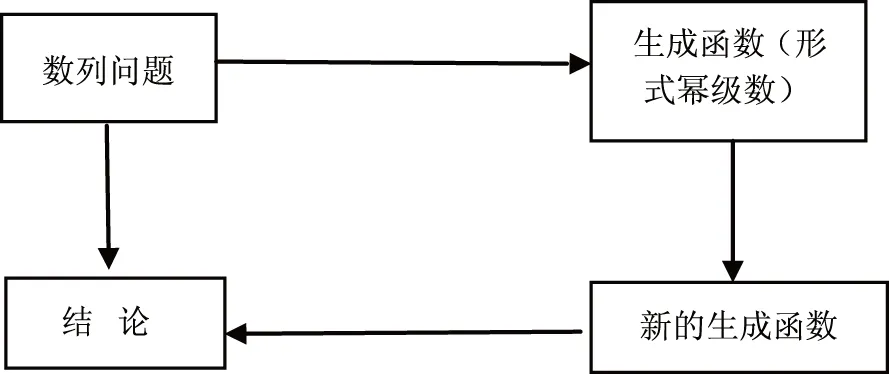
由这个框图可知,在运用生成函数处理问题时，需要解决以下两个问题：

①如何由数列{an}求出其生成函数g(x)；

②怎样把g(x)展开成所需要的级数，再通过对级数的运算来推得所要的结果。

2 生成函数在组合恒等式证明中的应用

2.1 二项式系数恒等式的证明

二项式定理在组合数学中占有非常重要的地位，以二项展开式作为生成函数来推导或证明一些组合恒等式也是特别常见且重要的方法。其一般思路是，先观察欲证恒等式两边的特点，然后构造合适的生成函数，再通过比较等式两端对应项的系数，来得到要证的恒等式。

下面我们结合具体的例子来说明生成函数在证明二项式恒等式中的应用：

例2.1： 求证：

析：观察可知恒等式的左边比较复杂，直接通过组合计数公式去化简证明会有些困难。但是，通过观察我们发现等式左端的规律性还是比较强，为此设法构造以二项展开式为生成函数的函数模型，即设法构造这样的生成函数，它以等式左端作为确定项的系数，再对所构造的生成函数进行化简处理，看能否得到右端对应的系数。

证明：我们构造如下生成函数：

g(x)=(1+x)+2(1+x)2+3(1+x)3+…+n(1+x)n

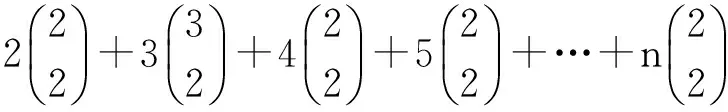
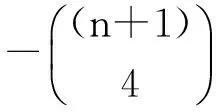
两端是同一生成函数对应项的系数，所以即证得结论，证毕。

又如我们可以用生成函数证明Vandermonde恒等式。

例2.2: (Vandermonde恒等式)设α，β为非零实数，则

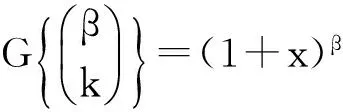
由结论的唯一性知，

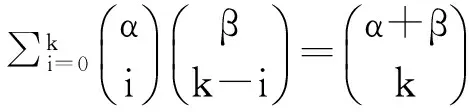
证毕。

同理，还可以证明对任意的正整数p,q有如下组合恒等式：

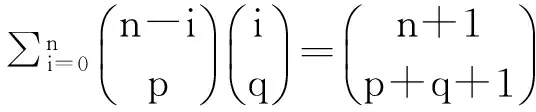
小结：以二项展开式作为生成函数来证明组合恒等式，其方法是适当地选取两个或多个二项式，使它们的乘积中对应项的系数恰为所要证的恒等式，或者经过适当的化简处理得到欲证的恒等式。以二项展开式作为生成函数来证明一些组合恒等式是最为基础的一类用生成函数证明组合恒等式的方法。

2.2 整数分拆恒等式的证明

在18世纪，Euler在研究正整数的分拆时首先使用了生成函数这一工具。19世纪初，Laplace在研究概率问题时，使得生成函数理论得到进一步发展与丰富。我们知道在整数分拆中也有许多恒等式，比如Euler恒等式、Rogers-Ramamujan 恒等式等，这些都是非常经典的恒等式，此外还有很多各种各样的分拆恒等式，它们在分拆理论中扮演着重要的角色，这些恒等式中的许多都可以用生成函数的方法来研究和证明。

下面先来介绍几个有关整数分拆的生成函数理论：

定理2.1[4]假设有p种类型的对象，且每一类型i有ni个不可区分的对象，i=1，2，…，p.假如每一种类型的对象可以选择任意多个，则选取n个不同的对象的方法总数由如下生成函数中的的xn系数给出：

g(x)=(1+x+x2+…+xn1)(1+x+x2+…+xn2)…(1+x+x2+…+xnp)

定理2.2[4]将正整数n分拆成若干个正整数的和，分拆的个数用p(n)表示，若将n分拆为1，2，3…的和，且每部分都不重复的方案数为an的生成函数可写成：

g(x)=(1+x)(1+x2)(1+x3)…

若将n分拆为1，2，3，%…的和，允许分拆中各部分重复的方案数为bn的生成函数可写成：

g(x)=(1+x+x2+…)(1+x2+x4+…)(1+x3+x6+…)…

下面举一个例子来说明运用生成函数法来证明分拆恒等式所带来的优越性。

例2.1 已知正整数n的每部分只出现2,3或5次的分拆数记为p1(n),正整数n的每部分模12余±2，±3，6的分拆数记为p2(n),试证：p1(n)=p2(n).

证明：等式左边用生成函数表示为

右边用生成函数表示为

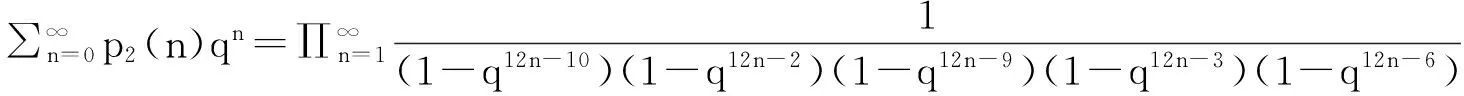
对左边的生成函数进行化简：

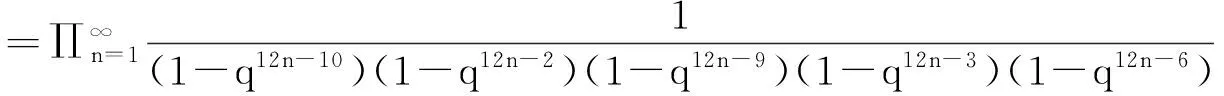
可以发现等式两边所对应的生成函数相同，所以有p1(n)=p2(n)，证毕。

小结：用生成函数法证明整数分拆恒等式是相当常见的方法，当然证明这类恒等式有时也会用到其他一些证明方法，例如组合证明法，但不可否认的是，有时借助生成函数来证明会带来很大的方便，能够达到很好的效果。

2.3 其他类型的恒等式的证明

除了上面所讨论的两类很常见的组合恒等式，其实还有很多其他类型的组合恒等式，比如可重集上的组合恒等式，Fibonacci恒等式等，这些恒等式的证明也可以借助生成函数这一工具，这一节我们简要介绍生成函数在可重集上的恒等式证明中的应用，先看一个引理：

引理2.3[5]对于|x|<1的任何x，有

证明：由于对于|x|<1的任何x，有

取α=-n(n为正整数),由

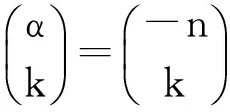
即证得引理，证毕。

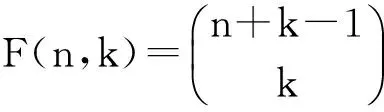
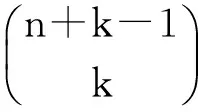
证明：假设ak表示从n个不同物体中允许重复地选取k个的方法数，由分析可知，序列{a0,a1,a2,…,ak,…}的生成函数为

由引理2.3可得，

所以得到

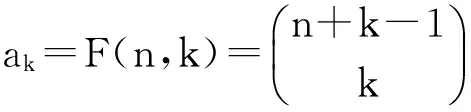
证毕。

3 生成函数在组合计数和整数分拆理论中的应用

3.1 生成函数在组合计数理论中的应用

组合计数是组合数学中非常重要的一部分内容，我们从高中开始学习的排列组合数就是用来计算一些具体问题的方法数，并为概率论与数理统计的学习与研究打下基础，两者紧密结合。因此，很有必要对组合计数进行研究，而生成函数作为一个极其重要的工具，借助它来研究和处理一些组合计数问题，有时会起到意想不到的效果。

现在我们先看几个问题：

例3.1： 一箱子内装有3个红球，2个黑球，4个白球，这些球除颜色外都相同，现在从箱子中任意取3个球，问有多少种不同的取法数？

解答：作形式表达式

(1+x+x2+x3)(1+x+x2)(1+x+x2+x3+x4)

若每次从箱子中取出n个的可重复组合数用an表示，则数列{an}的生成函数可表示为：

所以，生成函数f(x)的展开式中x3的系数9即代表从箱子中任意取3个球的所有不同方法数。

例3.2: 现有1分，2分，5分的邮票，问能贴出哪些面值(这里以角为单位)的邮票？每种面值又有多少种贴法？

解答：用an表示用1分，2分，5分的邮票，贴出面值为n的邮票的不同贴法总数，因邮票可重复使用，所以数列{an}的生成函数为

f(x)=∑n≥0anxn=(1+x+x2+x3+…)(1+x2+x4+…)(1+x5+x10+…)=1+x+2x2+2x3+3x4+4x5+…

由生成函数的展开式可得:

x表示贴出面值为1分的邮票共有1种方案:1.

2x2表示贴出面值为2分的邮票共有2种方案:1+1,2.

2x3表示贴出面值为3分的邮票共有2种方案:1+1+1,1+2．

3x4表示贴出面值为4分的邮票共有3种方案:1+1+1+1,1+1+2,2+2．

……

所以从上面的生成函数就可以得出能贴出哪些面值的邮票，以及每种面值的邮票的贴法总数。

以上是在现实生活中会遇到的具体例子，通过运用生成函数去处理，我们发现解决过程简单明了，并且易于掌握和运用。

3.2 生成函数在整数分拆理论中的应用

整数分拆与组合数学中的很多实际问题都有关联，即很多组合数学中的实际问题都可以看成是对某些整数按照给定的条件进行分拆，进而通过计算分拆的方法数来解决问题，而对于处理分拆问题，生成函数自然不失为一种非常有效的工具。

例3.3： 若有四种砝码各一枚，它们分别是1克、2克、3克、4克的,问能秤出哪几种重量? 有几种对应的方案?

解答：由分析计算可知，可以秤出的重量最少是1克,最多为10克，我们可以考虑将它转化为整数分拆问题，即转为计数将1到10的这10个数分别分拆成1、2、3、4的方法数。因此，可以考虑生成函数:

g(x)=(1+x)(1+x2)(1+x3)(1+x4)

这里砝码的克数用x的指数表示出来了，而对应的方案数则由x的系数表示。

将生成函数展开得：

g(x)=1+x+x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10

通过生成函数，所要的结果就很清晰，例如，右端有2x6项,说明秤出6克的方案数有两种,即6=1+2+3=2+4；又如x10项表示秤出10克的方案数仅有一种，即10=1+2+3+4.

例3.4： 求方程x1+x2+x3+x4=12,满足0≤x1≤5,1≤x2≤4,3≤x3≤7,4≤x4≤6的整数解的个数。

析：由分析可知此问题也可认为是整数分拆问题,也就是把12分拆成满足条件的4个整数的和的方法数问题。

解答：通过对问题的分析,构建如下生成函数:

g(x)=(1+x+…+x5)(x+x2+x3+x4)(x3+x4+…+x7)(x4+x5+x6)

g(x)的展开式中x12的系数a12即为所要求的满足条件的解的个数。可以解得a12=31即为所要的整数解个数。

小结：整数分拆问题是组合数学中一个十分重要而有趣的问题，而整数分拆问题研究中最重要的是讨论和研究分拆函数的一些性质，通过对分拆函数的运算和分析得到一些想要的结果。这其中生成函数则刚好成为一个十分有效的工具，所以分拆理论的研究很自然地会经常用到生成函数法。从上面的例题中我们会发现，组合计数与整数分拆有很多关联之处，许多整数分拆问题可以转化为组合计数问题，当计数问题解决了，整数分拆问题也可以得到解答。

4 生成函数在递推关系中的应用

递推关系是数学计算中用得特别多的一个工具,很多数学问题特别是组合数学问题都可以转化成递推关系问题，但是递推关系问题的处理并没有想象的容易，但是，如果能利用生成函数来求解递推关系问题，可能会收到意想不到的效果，可见生成函数法是处理递推关系问题的一种重要且行之有效的方法。

例4.1: 在n位十进制的数中，请问出现偶数个3的数有多少个？。

解：令an表示n位十进制数中出现偶数个3的数的个数,bn表示n位十进制数中出现奇数个3的数的个数。

所以有an=9×10n-2+8an-1,其中a1=8，此关系即为关于序列{an}的递推关系,求解此递推关系是解决本问题的关键。我们可以考虑引进序列{an}的生成函数f(x),即:

f(x)=a1+a2x+a3x2+…,

(1)

所以，8xf(x)=8a1x+8a2x2+8a3x3+…

(2)

(1)式-(2)式得：(1-8x)f(x)=a1+(a2-8a1)x+(a3-8a2)x2+…

又因为an-8an-1=9×10n-2,a1=8，

所以

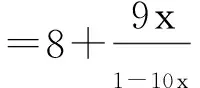
再将f(x)展开成如下形式的幂级数：

例4.2: 求递推关系fn=5fn-1-6fn-2(n≥2)满足初值f0=1,f1=-2的解.

解：先写出fn对应的生成函数f(x),并作如下变形：

f(x)=f0+f1x+f2x2+…+fnxn+…

-5xf(x)=-5f0x-5f1x2-5f2x3-…-5fn-1xn-…

6x2f(x)=6f0x2+6f1x3+6f2x4+…+6fn-2xn+…

注意到当n≥2时fn-5fn-1+6fn-2=0，将上面三式相加得到：

(1-5x+6x2)f(x)=f0+(f1-5f0)x=1-7x

由此便得到fn的生成函数为

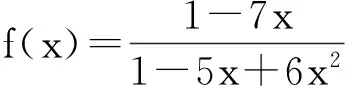
为了得到fn的通项公式，我们继续把f(x)展开成幂级数。这里用分解为部分分式的和的方法，写成

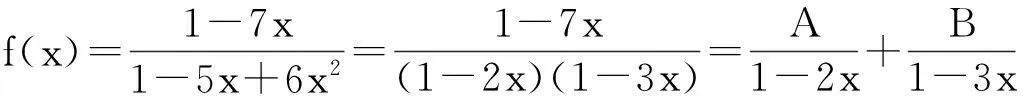
易得待定系数A=5,B=-4.所以

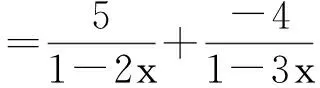
=1-(5×2-4×3)x+…+(5×2n-4×3n) xn+…

所以得到，

fn=5×2n-4×3n

由上面的求解过程，我们可以得到下面的结论。

结论4.1: 设数列{fn}满足如下递推关系

fn+a1fn-1+…+akfn-k=0(n≥k).

初值为f0,f1,…,fK-1,则数列{fn}的生成函数为

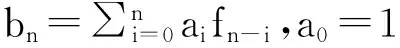
将bn的求和表达式展开以后即为：

由bn的表达式可知，不仅能由初值确定常数bi，反之，若已知常数bi，也可唯一确定初值f0,f1,…,fK-1，因为当把上面的关系式看成是关于未知数f0,f1,…,fK-1的线性方程组时，其系数矩阵为对角元全为1的下三角矩阵。同时注意到f(x)是一个有理真分式，故上面的定理也是可逆的。即有下面的结论：

结论4.2: 设数列{fn}的生成函数为

则数列{fn}满足如下递推关系

fn+a1fn-1+…+akfn-k=0(n≥k).

①给定一个数列的递推关系及其初值，如果这个递推关系是线性齐次常系数的，那么其生成函数为有理真分式，又由数学分析中的结论可知它一定是可以展开成幂级数的，从而可求得fn的通项公式。

②假如已经知道{fn}的生成函数为有理真分式，则一定可以找到{fn}的递推关系和初值，并且这个递推关系是线性齐次常系数的。

对于非线性齐次常系数递推关系，有如下的结论：

结论4.3: 设数列{fn}满足如下递推关系

fn+a1fn-1+…+akfn-k=hn(n≥k).

初值为f0,f1,…,fK-1,则数列{fn}的生成函数为

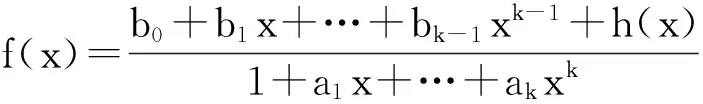
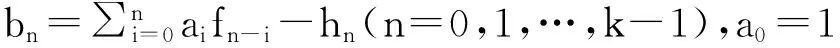
最后我们用生成函数来推导Catalan数[6]Cn的表达式。

我们知道Catalan数Cn满足下面的递推关系：

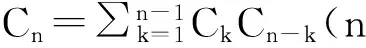
初值为C1=1.若补充定义C0=0，则

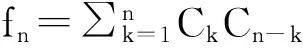
所以f(x)=C(x)-x.

又f(x)=C2(x),故C2(x)=C(x)-x，解之得

又因为C0=0意味着C(0)=0，故要舍去上式C(x)的解中相加的那一个，即只取

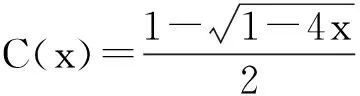
再将C(x)作幂级数展开，得到

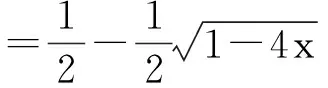
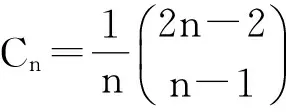
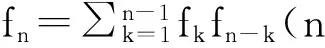
小结：通过利用生成函数求解递推关系问题，原本不好处理的问题会变得更加容易表达和处理。可以说，生成函数是解决递推关系问题的一个十分有效的工具，这里的关键点就是如何灵活地将递推关系问题转化为生成函数问题，有的时候可能生成函数并不好找，所以怎样去观察和发现其中可能有用的生成函数是关键的一步，因为这将为后面的处理过程带来许多简便。

5 总结

本文介绍了处理组合数学问题的一个极其重要的工具——生成函数，它在组合数学中的应用很广泛，我们主要研究了其在证明一些组合恒等式，解决一些组合计数问题、整数分拆问题、递推关系问题中的应用，其实它在处理其他一些问题中还有许多应用，比如在概率统计计算、图论、理论物理问题求解、计算机算法的复杂性分析等许多学科中都有着广泛的应用，对于这些应用本文没有涉及。总之，大量事例表明发生函数方法对组合数学中的许多问题的研究有着重要的意义,是研究组合数学的必不可少的工具,所以我们很有必要去学习和掌握它的基本理论知识，并能运用它来解决一些实际问题。

[1]柯召,魏万迪.组合论(上册)[M].北京:科学出版社,2010.

[2]卢光辉，孙世新，杨国武.组合数学及其应用[M].北京：清华大学出版社，2014.

[3]冯荣权,宋春伟.组合数学[M].北京:北京大学出版社,2015.

[4]George E.Andrews and Kimmo Eriksson.Ingeger partition[M].Cambridge: Cambridge University Press,2004.

[5]王天明.近代组合学[M].大连:大连理工大学出版社,2008.

[6]杨雅琴,李秋月,马腾宇.组合数学[M].北京:国防工业出版社,2013.

Some Application of Generating Function in Combinatorics

WANG Zhong-ping

(College of Mathematics and Statistics, Chongqing University, Chongqing 401331,China)

Generating function is an important theory tool in combinatorics.Its application in combinatorial problem is flexible and extensive. It not only can be used to deduce or prove all kinds of useful combinatorial identities, but also can be used to solve combinatorial counting problem,integer partition problem,recursive relations problem,etc.This paper mainly study the application of generating function in several combinatorial problems of the above listed, it can also reflect the superiority of generating function, a tool for us deal with combinatorial mathematics problems.

Generating function;Combinatorial identities; Combinatorial counting;Integer partition; Recursive relation

2016-02-17

王中平(1988-)，男，江西赣州人，重庆大学数学与统计学院在读硕士。主要研究方向：组合数学。

O174

A

1673-6125(2016)01-0001-07