探究一种非正弦周期变化的电流和电压的有效值

郑 金

(凌源市职教中心 辽宁 朝阳 122500)



探究一种非正弦周期变化的电流和电压的有效值

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

通过对两个不同形式的电路问题进行分析，得出相同形式的非正弦周期变化的电流和电压的瞬时值表达式，并对这种波动直流电用多种方法推导出有效值计算公式.

非正弦电流 有效值 竞赛题 一题多解

非正弦周期电流指的是不按正弦规律变化但具有周期性的电流，其有效值规定为：如果一个非正弦周期电流通过电阻R时消耗的功率跟一个恒定电流I通过同一电阻R时消耗的功率相同，那么这个恒定电流I，就叫做该非正弦周期电流的有效值.

对于由恒定电流与正弦交流叠加而成的非正弦的周期电流，其有效值可用一个导出公式来计算，但对于其他形式的非正弦周期电流却不能随意套用公式求有效值，否则会出错.下面通过两道例题来推导公式.

【例1】如图1所示，光滑长导轨PQ和MN固定在水平面上，左端连接电阻R=1 Ω，以M点为坐标原点，MN为x轴，MP为y轴建立坐标系，则PQ轨道的方程为y=1.5+0.5sin20πx(m).现紧靠MP垂直于MN放置一根光滑导体杆，长度为2 m，质量m=0.2 kg，整个装置处于磁感应强度大小B=1 T，方向竖直向下(垂直纸面向里)的匀强磁场中.导体杆从t=0时刻开始在水平向右的拉力F作用下以速度v=1 m/s从MP位置向右匀速运动，运动过程中杆与导轨保持良好接触，除R外其他所有电阻忽略不计.求电流随时间变化的表达式(以y轴正方向的电动势方向为正)和电流的有效值.

图1

解析:经过时间t导体杆的位移x=vt，则PQ轨道的方程为

y=1.5+0.5sin20πt(m)

感应电动势为

u=Bvy=1.5+0.5sin20πt(V)

电流为

这是波动直流电，属于非正弦的周期电流，可分解为恒定电流I1=1.5 A和正弦电流i2=0.5sin20πt两部分，则在一个周期T内通过电阻R产生的热量为

设原来电流的有效值为I，则在一个周期内有

Q=I2RT

联立方程可得

如果将一条导轨的形状由正弦曲线变为如图2所示的脉动曲线，其中每一段曲线为正弦曲线的半波，那么电路中产生电流的有效值是多少呢？

图2

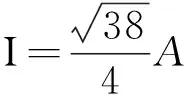
图3 图4

可见，对于以上两个电路而言，产生电流的有效值不同，因此求有效值的方法不同.

结论：对于电流i=I0+Imsinωt，其有效值为

含义：对于恒定电流i1与正弦交变电流i2的代数和i，其有效值I恰好等于恒定电流的有效值I1与正弦交变电流的有效值I2的平方和的平方根，即

该推论式只适用于波动直流i=I0+Imsinωt，不适用于恒定电流之和I=I1+I2，也不适用于脉动直流

【例2】(第一届全国中学生物理竞赛题)如图5所示的电路中，直流电源的电动势为5 V，正弦交流电源的电动势为3 V，则电阻R上的电压有效值为多少？

图5 图6

分析:当交流电在正半周时，直流电与交流电正向串联，二极管正向导通；当交流电在负半周时，直流电与交流电反向串联，由于直流电压大于交流电压最大值，则二极管仍正向导通，画出电压图像如图6所示.这是波动直流电，其大小按周期变化，由两部分叠加而成，其中一部分为恒定直流，另一部分为正弦交流，可知电路中电压的瞬时值为

图7 图8

图9

根据有效值的定义可知

所以电压的有效值为

结论:对于电压u=U0+Umsinωt，其有效值为

含义:对于恒定电压u1与正弦交变电压u2之和u，其有效值U恰好等于恒定电压的有效值U1与正弦交变电压的有效值U2的平方和的平方根，即

该推论式只适用于波动直流电压u=U0+Umsinωt，不适用于恒定电压之和U=U1+U2，也不适用于两个正弦交变电压之和

u=Um1sinωt+Um2sinωt

总之，恒定电流与正弦交流叠加形成直流的有效值等于直流有效值与交流有效值的平方和的平方根.

以上特殊公式及结论都是根据有效值的定义来计算一种特殊形式的电流和电压的有效值而得出的，下面从另外的角度来探讨一般公式.

即

这表明交流电的有效值等于瞬时值在一个周期内的方均根.还可用微积分形式表示为

对于非正弦的周期量，如果不用微积分，可分三步求有效值，即对瞬时值先平方,再平均,后取平方根.

第一步：平方

利用半角公式

可得

第二步：平均

第三步：开方

所求有效值为

第一步：平方

利用半角公式可得

第二步：平均

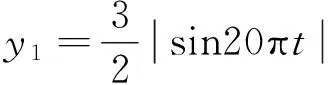
第三步：开方

所求电流的有效值为

此外，由电工学可知，一个非正弦波的周期信号，可以看作是由一些不同频率的正弦波信号叠加的结果，或者说，任何非正弦的周期信号都可以分解成一系列频率成整数倍的正弦成分，把这些正弦成分叫做这个非正弦周期信号的谐波分量.对于非正弦波中的直流分量，可看作是频率为零的正弦波.

非正弦的周期电压可表示为

其中U0为直流分量，U1,U2,…为各交流分量的有效值.

根据有效值的规定和数学推导可以得出非正弦周期电压的有效值计算公式为

即非正弦周期电压的有效值等于各谐波分量有效值平方和的平方根.

对于非正弦周期电压

是一种最简单的非正弦周期电压，其中两个谐波电压的有效值分别为5 V和3 V，所以,加在电阻两端的非正弦交流电压的有效值为

由此可见，对同一非正弦周期电压有效值问题，多种解法得到同一结果，殊途同归.

总之，非正弦周期量的有效值，等于它的直流分量、基波和各高次谐波有效值平方和的平方根.

特殊情形是，恒定电流与正弦交变电流叠加所形成波动直流电的有效值等于直流有效值与交流有效值的平方和的平方根.这是一种最简单的非正弦周期电流有效值的计算方法.考虑到非正弦的周期电流有多种形式，因此在利用推论式计算有效值时，要注意其适用范围，不能生搬硬套.

1 王志刚.对一道有效值试题的研究.物理教学，2014(2)

2 吴万盛.一道物理竞赛题的新解法.物理通报，2005(12)

3 王力航.由一道竞赛题谈交流直流叠加时有效值的求法.中学物理教学参考，2008(10)

4 李庆国.关于一个“有效值”问题的讨论.中学物理，2005(8)

5 朱建廉.一类交变电流有效值的求解方法研究.物理教师，2005(10)

6 周绍敏.电工基础(第3版).北京：高等教育出版社，2005.270

2015-05-22)