红外成像系统的非均匀性实时校正

李赓飞，李桂菊，韩广良，刘培勋，江 山

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)



红外成像系统的非均匀性实时校正

李赓飞*，李桂菊，韩广良，刘培勋，江 山

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

针对红外相机系统响应非均匀性所产生的竖条纹固定噪声，提出了基于多线程优化的单帧红外图像非均匀性实时校正算法。该算法参考全变分理论的非均匀性校正算法确定噪声与图像输出之间的加性校正关系，建立了描述条纹噪声的数学模型；通过滤波算法将图像分为高频分量和低频分量，运用建立的条纹噪声模型，基于最小二乘法从高频部分中拟合出条纹噪声。最后，使用全变分理论确定的加性关系对图像进行校正。为了提高算法的计算速度，运用多线程技术对算法进行了优化。对提出的算法与MIRE(Midway Infrared Equalization)算法及传统双边滤波算法进行了图像质量评价和性能对比。结果显示：本文算法使图像非均匀性较原图降低了3%；算法效率与MIRE算法无异，系统运行时间在320×256的14位红外图像上为1.5 ms/frame，达到了工程标准。

红外图像；成像系统；竖条纹噪声；非均匀性校正；实时处理

1 引 言

受材料和工艺水平的限制，红外焦平面阵列(Infrared Focal Plane Arrays，IRFPA)各探测器单元之间普遍存在着响应非均匀性，此外，图像数据读出电路中各通道之间的差异会使这种非均匀性更加明显[1]。红外图像非均匀性主要分为时变噪声及固定噪声两类[2]，通过观察靶场实际图像发现，多数红外相机均表现出一定的非均匀性，这些非均匀性中对成像效果影响较大的是网状及条纹状噪声。对于红外图像中的垂直或水平线，难以判断其是场景目标自身的边缘还是由错误的固定模式噪声引起的，而传统的去噪方法常常会引起图像的过模糊化，在图像细节很低的红外图像中尤为突出。因此，研究如何有效去除固定噪声实现非均匀校正对于提高红外图像质量具有重要的实用价值。

目前针对IRFPA响应的非均匀校正算法主要包括基于标准源定标和基于场景的校正方法两类。基于参考源定标类方法是早期提出的一种易于实现且较有效的方法。典型的如一点校正法，两点校正法，多点校正法[3-4]等。这类方法一般通过更新非均匀性校正算法的参数实现，且需要一个额外的电子设备，进行多次重复定标。不但增加了系统复杂度，还会打断图像采集过程。在此基础上，人们提出了基于场景的非均匀性校正算法[5-9]，如基于恒定统计算法[5]，神经网络算法[9]。这些基于场景的算法主要根据实际场景提取校正系数，可以自适应地校正探测器因温度和时间漂移引起的变化。为了估计出可靠的参数，这类算法需要利用一组图片进行提前训练，一般收敛速度较慢，并且场景的帧间差异要足够小。如果图像序列帧间的差异过大，则在当前图像上会有前一帧图像遗留的残影，而校正残影的问题也是最近很多新算法必须研究的课题[7-8]。上述两类非均匀校正算法具有普遍性，对于条纹噪声，有时达不到满意的效果。因此一些文献又提出了针对性更强的算法[10-14]，例如基于小波的改进算法[10]，基于全变分理论的非均匀校正算法[11]，基于双边滤波的算法[12]，有的甚至直接从直方图的特征来考虑[13-14]，目前效果比较好的是文献[14]中提出的Midway InfRared Equalization(MIRE)算法，但以上算法在处理效果和运算速度的平衡上不能令人满意，在应用到实际工程中需要一定的取舍，有时还会使架构变的复杂。

本文为解决实际工程中红外相机普遍遇到的非均匀性问题，针对条纹样式噪声进行研究，参考全变分理论分析了图像与噪声的加性关系，建立了描述竖条纹噪声的数学模型，提出了一种简单的基于单帧的条纹状噪声校正算法，从根源上避免了残影现象，并运用多线程技术分析优化了算法，能够高速实时地对图像进行处理。

2 传统去噪原理及校正模型

2.1 传统图像去噪原理

一般图像大多采用滤波算法进行去噪，这类滤波器通过对邻域像素的加权平均来获取原始信号的可靠估计。其公式如下：

P(x)=k-1∫ΩI(y)fs(‖y-x‖)dy，

(1)

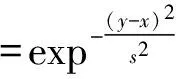
当图像存在边缘时，仅根据空间距离做处理，往往会使边缘过度平滑，从而造成图像模糊。而双边滤波器的主要思想是在空间位置上的加权操作中引入值域(像素值)加权，也就是说在分配图像邻域权值时，不仅考虑到了空间上是否相近，也考虑到了值域上是否相近，值域越相似，分配的权值也就越大，因此双边滤波也是一种非线性滤波器，加权组合后的双边滤波公式如下：

P(x)=k-1∫ΩI(y)fs(‖y-x‖)·

fr(I(y)-I(x))dy，

(2)

双边滤波器综合考虑了值域(像素值之间的相似程度越大权值越大)与定义域(像素之间的距离越相近权值越大)，再分配权值，从而减少了去噪过程中图像边缘的过度平滑现象，在一定程度上保证了图像边缘。

2.2 非均匀校正模型

在红外图像中，由非均匀性造成的图像退化是极其普遍的现象，而实际信号响应值和红外线光子流间的关系正是非线性的。所以在多数文献中，通用的非均匀性校正摄动模型为：

I(i，j)=g(S(i，j))+r(i，j)，

(3)

其中：(i，j)为像素坐标，I(i，j)为采集到的图像，S(i，j)为真实红外图像，g(x)是关于传感器的转变函数，而r(i，j)则表示其他的随机噪声。

非均匀校正算法的主要目的就是找出针对每一个传感器的g(x)函数，并对r(i，j)进行适当的优化。

2.3 条纹校正模型

目前靶场上常见的红外图像中，以竖条纹样噪声对成像的影响最为显著。为了简化问题，将红外相机的每一个传感器在响应时均近似为线性模型，这样它们的输出形式为：

I(i，j)=g(i，j)*S(i，j)+o(i，j)+r(i，j)，

(4)

其中：(i，j)为像素坐标，I(i，j)为采集到的图像，S(i，j)为真实红外图像，g(i，j)和o(i，j)两个函数分别表示第(i，j)个传感器的增益和偏移，而r(i，j) 表示其他的随机噪声。

3 实时红外图像的非均匀性校正算法

3.1 红外噪声模型的建立

全变分理论将图像定义为一个二维空间上的有界变差函数，并假设非均匀条纹噪声是一个固定的加性噪声，因此采集到的图像I(i，j)可分为两部分：

I(i，j)=S(i，j)+N(i，j)，

(5)

其中：N(i，j)为条纹噪声，S(i，j)为真实的红外场景，I(i，j)为采集到的红外图像。

鉴于全变分理论的思想，可以将式(5)代入式(4)得到新的式(6)：

N(i，j)=(g(i，j)-1)*S(i，j)+o(i，j)+r(i，j).

(6)

由于竖条纹噪声属于固定噪声，所以公式(6)中的增益g(i，j)和偏移函数o(i，j)在时间上的变化是十分缓慢的，可以认为g(i，j)和o(i，j)为常数。针对条纹噪声，假设随机噪声为零，可得条纹噪声公式为：

N(i，j)=a1*I(i，j)+a0.

(7)

虽然公式(7)为线性模型。但根据多项式的形式，不难将其扩展为高阶的非线性模型，即：

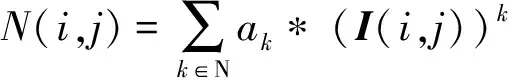
(8)

其中：N(i，j)为竖条纹噪声，I(i，j)为采集到的图像，ak(k=1，2，3，…)为误差参数，k为多项式阶数。

若对图像中的像素逐一进行处理，则对每个像素都需要一组参数ak(k=1，2，3，…)来进行校正，导致算法复杂度极高，因此本文针对竖条纹固定噪声，采用以列为整体的处理策略，对公式(8)增加简单约束：

(9)

其中：j表示图像的任意列，这样针对每一列，求出一组参数ak即可。

3.2 单一图像的非均匀性校正算法

综上所述，本文采用的算法流程如图1所示。由式(2)分离出高频分量和低频分量，具体步骤为：高频分量包含了图像部分边缘细节以及竖条纹固定模式噪声，以原始图像作为输入，通过式(9)与高频分量拟合，得出纯条纹噪声图像，最后将条纹噪声带入式(5)得到校正后的图像。

图1 NUC算法流程

算法拟合过程中，以列为单位通过寻找最优解的方法，使得条纹噪声与高频分量差异最小。从而将问题转化为最小二乘优化问题，得到成本函数E(A)：

Ej(A)=(Nj(i)-Hj(i))2，

(10)

其中：Ej(A) 为第j列成本函数，Nj(i)为条纹噪声，以采集到的红外图像作为输入，根据式(9)得出，k为多项式阶数，Hj(i)为双边滤波分离出的高频分量。

使成本函数Ej(A)最小，令其为零，再将式(9)带入可得：

(11)

将式(11)中的I(i)k写成系数矩阵P：

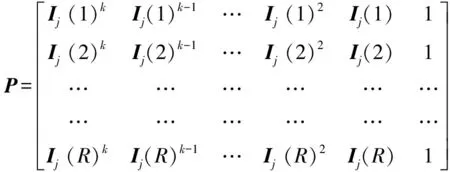
(12)

其中：R为图像行数，则系数向量A=(a0，a1，a2，…，ak)的求解公式为：

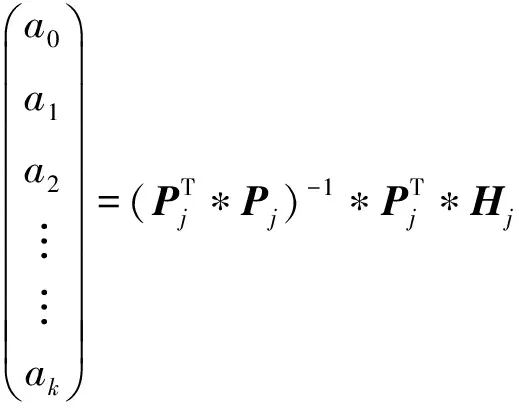
(13)

其中：H为经双边滤波处理后得到的高频分量。Pj为j列的Ik～I以及常量1组成的(k+1)×R矩阵，R为图像总行数。Hj为图像高频部分的j列。

4 实验结果与分析

4.1 实验设备

本文算法在Matrix MCX-6300嵌入式工控机(CPU：8核酷睿i7，主频：2.30 G，内存4 G)上运行，使用了Matrox solios eCL/XCL-B图像采集卡和Matrox vio图像处理卡作为图像输入输出卡。以Visual Studio 2010为编译环境，运用MFC搭建了系统框架，算法代码调用了OpenCV 2.4.9库。红外热像仪采用分辨率为320×256的14 bit图像，输出帧频有三档，分别为50，100，200 Hz 可变。

4.2 参数设置

本文可调节的参数主要有3个，其中两个为双边滤波中空域及值域的相似参数，经试验测试知，空域的相似参数对算法影响较小，而值域的相似参数对条纹大小较为敏感，本文试验取空域相似参数为10，值域参数为3。

k值的设置方法如下，在k=0时，公式(9)变为Nj(i)=aj0，可以看到误差与输入图像边缘无关，因此校正并不能使图像在有目标前景时得到满意的结果。而当k>0时，公式(9)中N为I的函数，误差随输入图像的不同而变化，使得在不同场景下具有不同的校正值。条纹噪声的计算过程如图2所示，实验采用320×256的14位红外图像，从图中可以看出，当k取较大值时，条纹噪声变化不明显，而处理时间却有所增加。综合考虑运行效率及校正效果，本文采用k=1。

k=0，t=17.51 ms

k=1，t=18.39 ms

k=2，t=20.21 ms

k=3，t=21.70 ms

4.3 算法对比及质量评价

图像质量的评价实验在分辨率为320×256的14 bit 图像上进行，本文选取MIRE算法，双边滤波算法作为对比算法，从参照处理时间(t)、信噪比(SNR)、平方差误差(MSE)、图像粗糙度(ρ)及国家标准的非均匀性响应率(UR)几方面进行分析。

表1 几种算法性能对比

算法质量评价结果如表1所示，可见，本文算法的运算时间远小于MIRE算法，而信噪比略高于MIRE算法；通过比较MSE可知，本文算法对原图的改动较大，仅次于双边滤波方法，但是双边滤波方法对原图像的模糊作用在图像粗糙程度这一指标中有所体现；ρ表示图像的粗糙程度，即高频信息。分析得到以下结论：ρ越大，算法保留的边缘越好，相较其他算法，本文算法的边缘保留效果更好。本文的非均匀响应率较原图降低了3%。

几种算法对3种图像的处理效果如图3～5所示。从图3可以看出，本文算法的视觉效果与MIRE相当，而运算时间远低于MIRE算法。对于图4的无条纹噪声图像，本文算法对原图的失真没有过增强，对于图5的存在条纹边缘干扰的图像，本文算法并没有出现明显的边缘去除现象。

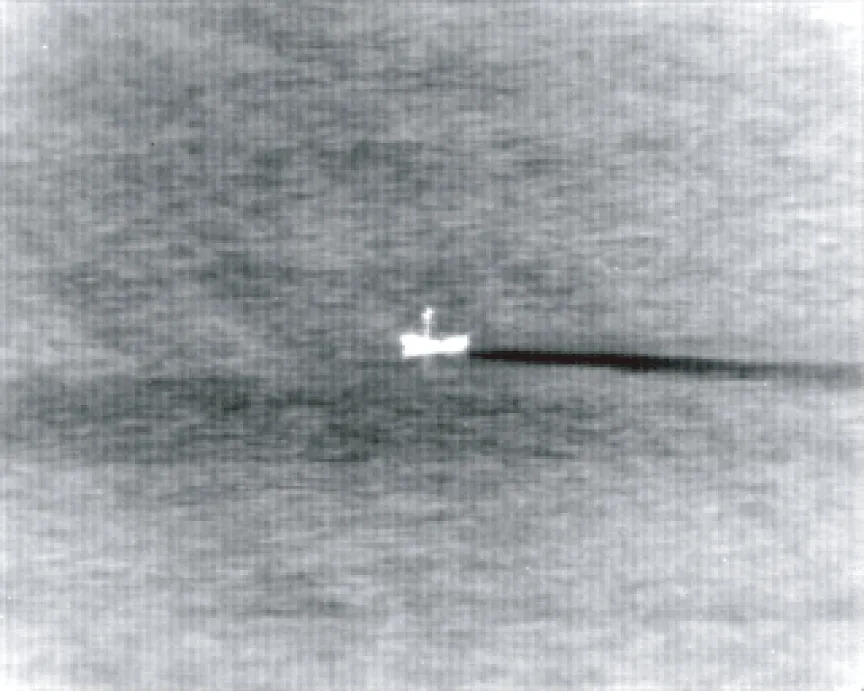
(a)原始图像

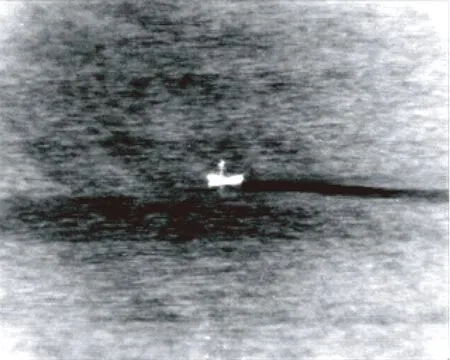
(b)MIRE算法结果

(c)双边滤波算法结果

(d)本文算法结果

Fig.3 Performance comparison of different algorithms in sea with complex background

(a)原始图像

(b)MIRE算法结果

(c)双边滤波算法结果

(d)本文算法结果

(a)原始图像

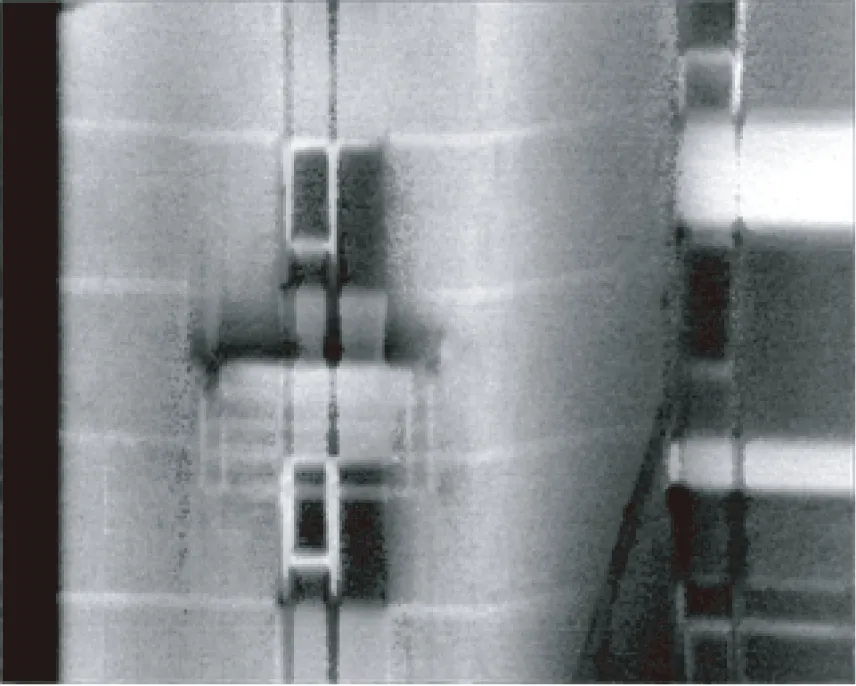
(b)MIRE算法结果

(c)双边滤波算法结果

(d)本文算法结果

4.4 多线程优化策略

多线程技术是使计算机可以在同一时间处理不同任务，可以提高算法的运算速度。鉴于实际应用需求，本程序启用了4个线程：图像输入、图像输出、竖条纹噪声估计和图像校正。

图像输入使用双内存的乒乓操作来捕获图像，可与其他线程并行运行；条纹噪声的估计以一个辅助线程做运算。由于竖条纹噪声的固定特点，可以近似认为其在短时间内变化极小，则对于图片序列中邻近帧的校正可以用同一条纹噪声图片重复进行处理。该线程循环地复制当前最新图片，并作为输入，计算条纹噪声后再存储图片；图像校正线程时，则使用已估算出的条纹噪声图片，根据公式(5)进行校正操作。最后，图像输出线程经过自适应直方图拉伸算法，将校正后的14位图像实时转化成8 bit图像并显示。这种策略的原理性缺陷在于近似认为条纹噪声在短时间内是不变的。若辅助线程估计噪声耗时过多，则会导致条纹噪声更新过慢，校正不准。

以帧频为200 Hz的相机为例，假设算法噪声估计时间为20 ms，辅助线程每4帧估计出一张噪声图像，随后根据噪声图像和当前采集到的图像进行校正，并即时对最新的图像进行新的噪声估计，以更新噪声图像。线程工作安排如图6所示，其中Fx表示第x帧图像，M1，M2表示乒乓操作的缓冲区，横线“—”表示处理中，Nx表示图像根据第x帧估计出的噪声，FxNy表示第x帧图像根据第y帧估计噪声进行校正的结果，Dx表示转换后的显示结果。图6中噪声估计线程在复制输入信息后便在后台单独运算，实测系统从帧信号开始到显示图像完成的周期为1.5 ms 左右，其中：采集图像与噪声估计都是异步处理，在时间上与图像显示是并行的，采集时间和估计时间均不包含在内，而有效占用时间包括校正图像耗时(≈1.15 ms)和输出转换图像耗时(≈0.35 ms)两部分。

本文算法对实验用条纹噪声图像的估计处理时间小于20 ms/frame，在200FPS的成像系统下的更新延迟仅为4 frame。而MIRE算法是以列为单位对图像进行中值直方图均衡化处理的，故算法运算量大，耗时达1 000 ms，导致其更新的条纹噪声与当前帧差异过大，容易引起校正错误。

图6 多线程工作安排

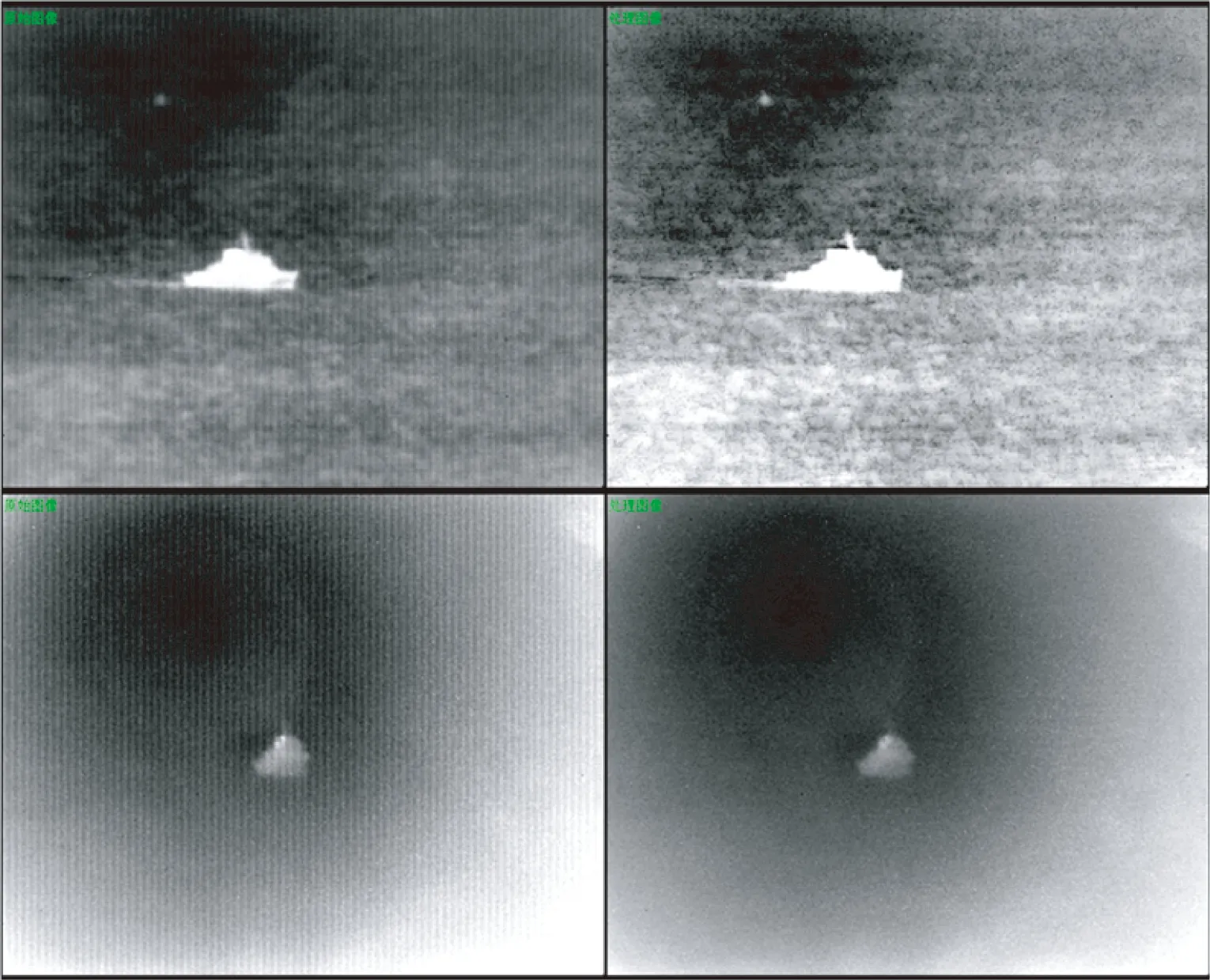
图7 算法多线程处理效果

实际间隔帧数以辅助线程的计算效率为准，结果表明图像显示周期约为1.5 ms，经多线程优化后，算法的处理时间较单线程提升了近10倍，而且处理结果与其并无明显差异。与经纬仪对接的实际处理效果如图7所示。

5 结 论

针对红外相机的非均匀性对成像影响较大这一问题，本文研究了单帧的实时校正算法，从根源上避免了基于场景算法的残影现象，并结合噪声特点对算法进行优化。最后在分辨率为320×256的14位红外图像上进行了性能验证实验，并将MIRE、双边滤波算法作为对比算法，进行处理效果及时间对比实验。实验结果证明：算法在分辨率为320×256的14位红外图像上的运算时间为1.5 ms/frame，在200 FPS的成像系统上能够达到实时处理。较好地保持了图像边缘，非均匀响应率较原图像降低了3%。

[1] 刘永进，朱红，赵亦工. 基于红外焦平面阵列读出结构的非均匀校正算法[J]. 光学 精密工程，2008，16(1)：128-133. LIU Y J， ZHU H， ZHAO Y G. Nonuniformity correction algorithm based on infrared focal plane array readout architecture[J].Opt.PrecisionEng.， 2008， 16(1)： 128-133.(in Chinese)

[2] 曹扬，金伟其，刘崇亮，等. 红外焦平面阵列的自适应非均匀性校正及硬件实现[J]. 光学 精密工程，2011，19(12)：2985-2991. CAO Y， JIN W Q， LIU CH L，etal.. Adaptive nonuniformity correction and hardware implementation of IRFPA [J].Opt.PrecisionEng.， 2011， 19(12)： 2985-2991.(in Chinese)

[3] 代少升，张新立. 利用单片可编程系统对红外焦平面阵列进行实时非均匀性校正[J]. 光学 精密工程，2009，17(4)：854-858. DAI SH SH， ZHANG X L. Real-time nonuniformity correction of infrared focal plane arrays by system on programmable chip [J].Opt.PrecisionEng.， 2009，17(4)：854-858.(in Chinese)

[4] 张红辉，罗海波，余新荣，等. 多点标定的自适应非均匀性校正方法[J]. 红外与激光工程，2014，43(11)：3651-3654. ZHANG H H，LUO H B，YU X R，etal.. Adaptive non-uniformity correction algorithm based on multi-point correction [J].InfraredandLaserEngineering， 2014，43(11)：3651-3654.(in Chinese)

[5] 代少升，张天骐. 基于非线性响应的红外焦平面阵列非均匀性自适应校正算法[J]. 光学 精密工程，2008，16(4)：714-719. DAI SH SH， ZHANG T Q. Adaptive nonuniformity correction algorithm for IRFPA with nonlinear response [J].Opt.PrecisionEng.， 2008，16(4)：714-719.(in Chinese)

[6] NING L，JUN X.Inter frame phase-correlated registration scene-based nonuniformity correction technology [J].InfraredPhysics&Technology， 2015，69： 198-205.

[7] PABLO M， GUILLWEMO M， SERGIO T，etal.. Simultaneous digital super-resolution and nonuniformity correction for infrared imaging system [J].AppliedOptics， 2015，54(21)： 6508-6515.

[8] FAN F， MA Y， HUANG J，etal.. A combined temporal and spatial deghosting technique in scene based nonuniformity correction [J].InfraredPhysics&Technology， 2015，71： 408-415.

[9] 段程鹏，刘伟，谢庆胜，等.改进的神经网络非均匀校正算法的研究与实现[J].光学学报，2015，35(7)：0710001. DUAN CH P， LIU W， XIE Q SH，etal.. Research and implementation of improved neural network non-uniformity correction algorithm [J].ActaOpticaSinica， 2015， 35(7)：0710001.(in Chinese)

[10] TORRES J，INFANTE S O.Wavelet analysis for the elimination of striping noise in satellite images[J].Opt.Eng.，2001，40(7)：1309-1314.

[11] 潘科辰，顾国华，陈钱，等.一种改进的全变分模型校正红外焦平面阵列条纹非均匀性[J].红外技术，2016，38(2)：138-143. PAN K CH，GU G H，CHEN Q，etal.. An improved total variation model for correcting the strip nonuniformity in IRFPA image [J].InfraredTechnology， 2016， 38(2)：138-143.(in Chinese)

[12] 王书朋，高腾.基于双边滤波器的红外图像条纹噪声消除算法[J].红外技术，2014，36(9)：728-731. WANG SH P，GAO T. Destriping method for infrared image based on bilateral filter [J].InfraredTechnology， 2014， 36(9)：728-731.(in Chinese)

[13] 张磊，王岳环，宋琼.红外焦平面条带状非均匀校正硬件实现方法[J].红外与激光工程，2015，44(10)：2886-2890. ZHANG L， WANG Y H， SONG Q. Hardware implementation of stripe non-uniformity correction method of infrared focal plane arrays [J].InfraredandLaserEngineering， 2015， 44(10)：2886-2890.(in Chinese)

[14] TENDERO Y，LANDEAU S，GILLES J.Non-uniformity correction of infrared images by midway equalization [J].IPOL， 2012：doi：10.5201/ipol.2012.

李赓飞(1989-)，男，吉林通化人，博士研究生，2012年于吉林大学获得学士学位，主要研究方向为图像和视频信息处理。E-mail：killcolours@126.com.

导师简介：

李桂菊(1964-)，女，吉林吉林人，研究员，博士生导师，1988年于中国科学院长春光学精密机械与物理研究所获得硕士学位，研究方向为图像和视频信息处理、DSP开发与应用。E-mail： lgjciom666@126.com

(版权所有 未经许可 不得转载)

Real-time non-uniformity correction of infrared imaging system

LI Geng-fei*， LI Gui-ju， HAN Guang-liang， LIU Pei-xun，JIANG Shan

(Changchun Institute of Optics， Fine Mechanics and Physics，ChineseAcademyofSciences，Changchun130033，China)

A real-time Non-Uniformity Correction(NUC) algorithm for a single-frame infrared image was proposed based on multi-thread optimization to correct the strip-type Fixed Pattern Noise(FPN) generated by non-uniformity response from an infrared camera. Firstly， the plus-relationship of the output value and the noise was determined by NUC algorithm based on total variation theory and a mathematical model was established to describe the strip noise. The image was split into a high-frequency component and a low-frequency component by filters， and the strip noise was fitted from the high-frequency component by the mathematical model. Finally， the real infrared image was restored by the plus-relationship obtained from the total variation theory. To improve the computing speed， the proposed algorithm was optimized with the multi-thread. The image quality evaluation of the proposed algorithm was carried out and its performance was compared with the Midway Infrared Equalization(MIRE) and the bilateral filter methods. Experimental results indicate that the proposed algorithm has reduced the response non-uniformity by 3% as compaired with original image according to national standard GB/T 17444-1998， and its efficiency is no difference with that of the MIRE. Moreover， system running time for an 14 bit infrared image with a resolution of 320×256 is 1.5 ms/frame， which meets the engineering requirements.

infrared image； imaging system； strip-type noise； non-uniformity correction； real-time processing

2016-05-13；

2016-06-20.

国家自然科学基金资助项目(No.61172111)

1004-924X(2016)11-2841-07

TN216

A

10.3788/OPE.20162411.2841

*Correspondingauthor，E-mail：killcolours@126.com