测控设备引导跟踪数据插值方法

庞岳峰，吴小东，牛攀峰

(酒泉卫星发射中心 指挥控制站，甘肃 酒泉732750)



测控设备引导跟踪数据插值方法

庞岳峰，吴小东，牛攀峰

(酒泉卫星发射中心 指挥控制站，甘肃 酒泉732750)

航天测控设备在引导跟踪时需要将转换后的方位、俯仰角度进行插值，在工程中尽可能采用易软件实现且不影响插值精度的插值方法。文中在介绍目前常用的Lagrange插值、Newton插值、Neville插值和Aitken插值4种方法原理的基础上，分析了4种插值下待插值点位置对插值结果的影响，通过实际算例得到结论。并讨论了4种方法在测控设备引导跟踪数据插值方面的优缺点，得出在航天测控设备引导跟踪插值时使用Neville算法最好的结论。

测控设备；引导跟踪；Neville插值；Lagrange插值

航天测控设备在航天器发射任务中主要承担目标跟踪、测量、控制任务，程序引导跟踪是测控设备的跟踪方式之一[1]。程序引导跟踪原理是事先将目标理论弹道装订于测控设备跟踪单元，收到起飞信号后跟踪单元依据理论弹道转换为设备跟踪的A-E-R(方位-俯仰-距离)，最后控制天线按此A-E角运转。目前测控设备装订的弹道都是1组/s，设备在进行引导时采用Lagrange算法插值为20组/s或者40组/s。

插值点在已知节点中间的称为内插，在节点外面的称为外推。插值的方法有多种，目前常用的有Lagrange插值、Newton插值、Neville插值和Aitken插值等[2-7]，这些方法在GPS卫星精密星历差值方面的研究较为广泛[8-10]，在航天测控设备引导跟踪数据的插值研究较少。

1 插值方法及原理

1.1 Lagrange插值

在数值计算方面，关于多项式插值的方法有多种，其中拉格朗日插值法是既简单而又实用的方法。

设有行n个节点时刻t1,t2,…,tn，对应的理论弹道角度为f(t1),f(t2),…,f(tn)，则任意时刻的经过这n个点的n-1阶拉格朗日插值多项式P(t)的表达式为[3]

(1)

式中,Kn,i(t)是关于n个点xi(i=1,2,…,n)的拉格朗日基函数，其具体形式为

(2)

1.2 Neville插值

Neville插值是基于这样一个事实：对于两个低次多项式经过线性插值，能够得到高一次的插值多项式。如对于3个二维点(t0，y0)，(t1，y1)和(t2，y2)，yi=f(ti) ，i=0,1,2。设(x0，y0)和(t1，y1)两点的Lagrange线性插值为P0,1(t)，(t1，y1)和(t2，y2)两点的Lagrange线性插值为P1,2(t)。则

(3)

(4)

容易验算，P0,1,2(ti)=yi，i=0,1,2。即此时P0,1,2(t)为f(t)关节节点t0，t1，t2的的二次插值多项式。这种插值方法记为Neville插值。

进一步，用类似的方法定义P2,3(t),P3,4(t)，…，P(n-2),(n-1)(t)。对高阶多项式进行类似定义，直至P0,1,2,...,(n-1)(t)，它是对所有N个点的插值多项式的值，即所求的解。各个不同的P形成一张“表”，左边为“祖先”，一直到右边的一个“后代”，Neville插值计算如表1所示[5]。

表1 Neville插值计算表格

Neville方法用递推的方法填写表中的数据，从左到右每次一列，其递推公式为

(5)

其中，i=0,1,…,n，m=0,1,…,n-i。

1.3 Newton插值

同样设有行n个节点时刻t1,t2,tn，对应的理论弹道角度为f(t1),f(t2),…,f(tn)，则牛顿插值的表达式为[6]

Pn(t)=f[t1]+f[t1,t2](t-t1)+…+

f[t1,t2…tn](t-t1)(t-t2)…(t-tn-1)

(6)

其中，f[t1,t2…tk]为t1,t2…tk的k阶差商，并规定

体育产业的崛起，为体育特色小镇发展提供了重要的资金支持，也为体育特色小镇发展提供了重要的人员循环参与的动力保障。当前，国家对体育事业的大力支持是体育产业发展的黄金时期，也是体育特色小镇建设的绝佳机遇。

f[t1]=f(t1)

f[t1,t2]=(f(t1)-f(t2))(t1-t2)

f[t1,t2,t3]=(f(t1,t2)-f(t1,t3))(t1-t3)

f[t1,t2…tn]=(f(t1,t2…tn-1)-f(t1,t2…tn))(t1-tn)

而Pn(t)即为所需内插节点的对应位置的插值结果。

1.4 Aitken插值

采用与Neville插值不一样的节点，产生了另一种不同的逐步线性插值方法—Aitken插值，Aitken插值的构造是基于这样的直观想象：平面上的两个点可以连成一条直线，对应一个线性函数，把线性函数看作形式点，经线性组合构成二次函数，将二次函数再看作形式点，经线性组合构成三次函数。

表2 Aitken插值计算表格

Aitken插值用递推的方法填写表中的数据，从左到右每次一列，其递推公式为

(7)

2 实例分析

选用火箭厂家提供的某次任务20点/s的精确弹道分析，把它作为真值，然后抽取1点/s弹道，用不同插值方法内插结果进行比较。此时，插值点位于节点中间附近位置。分别运用4种内插方法，使用不同阶数得到的A-E-R以及它们与真值的差值如表3所示。

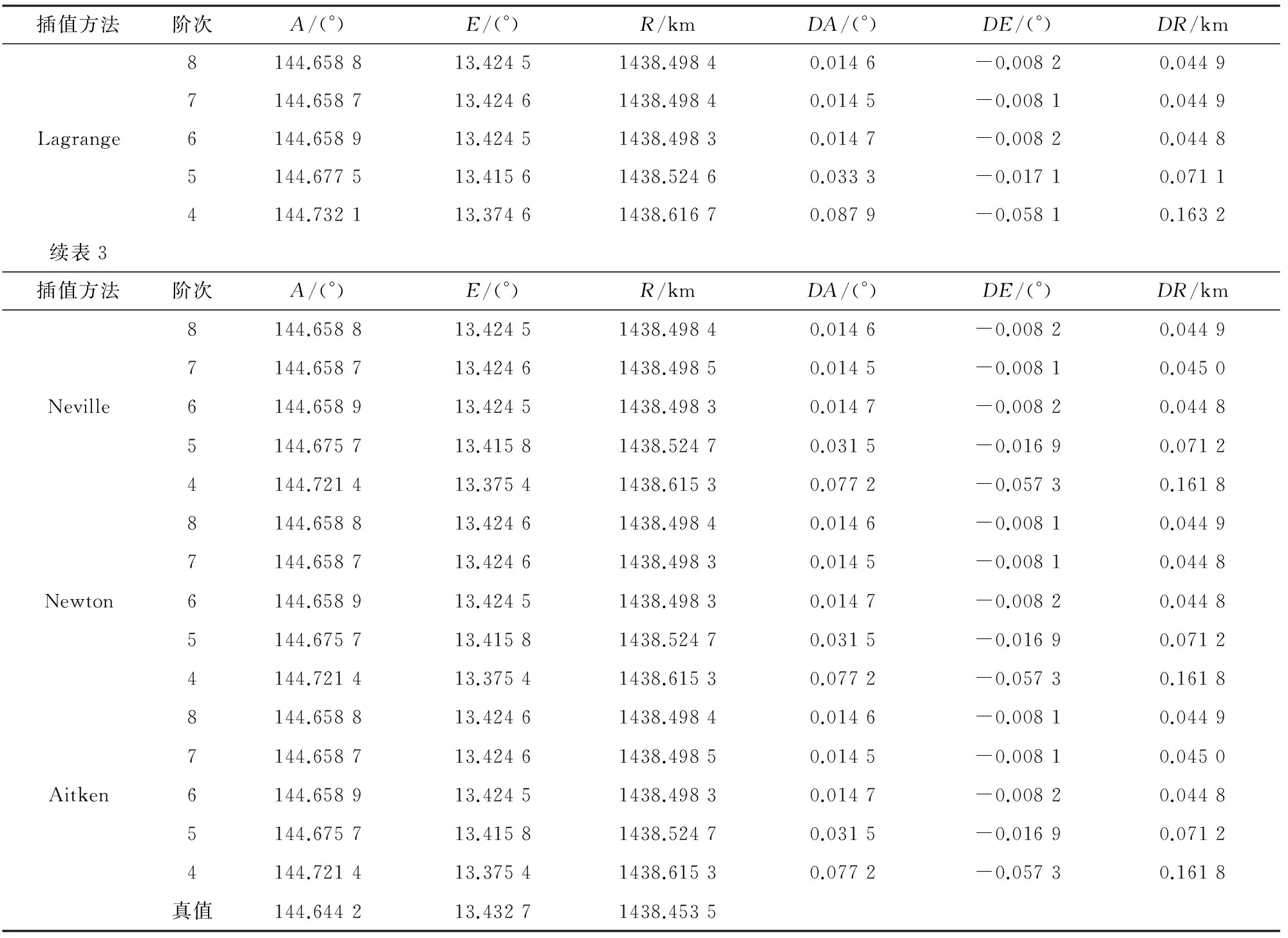
表3 插值点位于中间时的插值结果及其与真值的差值

表3中发现当插值阶数>6阶时，4种插值方法表现出一致性，4种插值方法的角度误差都<0.015°，距离误差<0.05 km，满足目前测控设备跟踪精度的要求(光测、雷达、遥测和统一测控系统中对精度最高的要求是随机误差<0.02°)。但是随着阶数的提高，插值精度并没有明显提高。插值阶数为5阶以下时精度有明显下降，不能满足要求。当插值点位于所选取节点的两端时，选取精确弹道的另一个点来分析，此时刻真值如表4所示，4种方法的插值结果如表4所示。

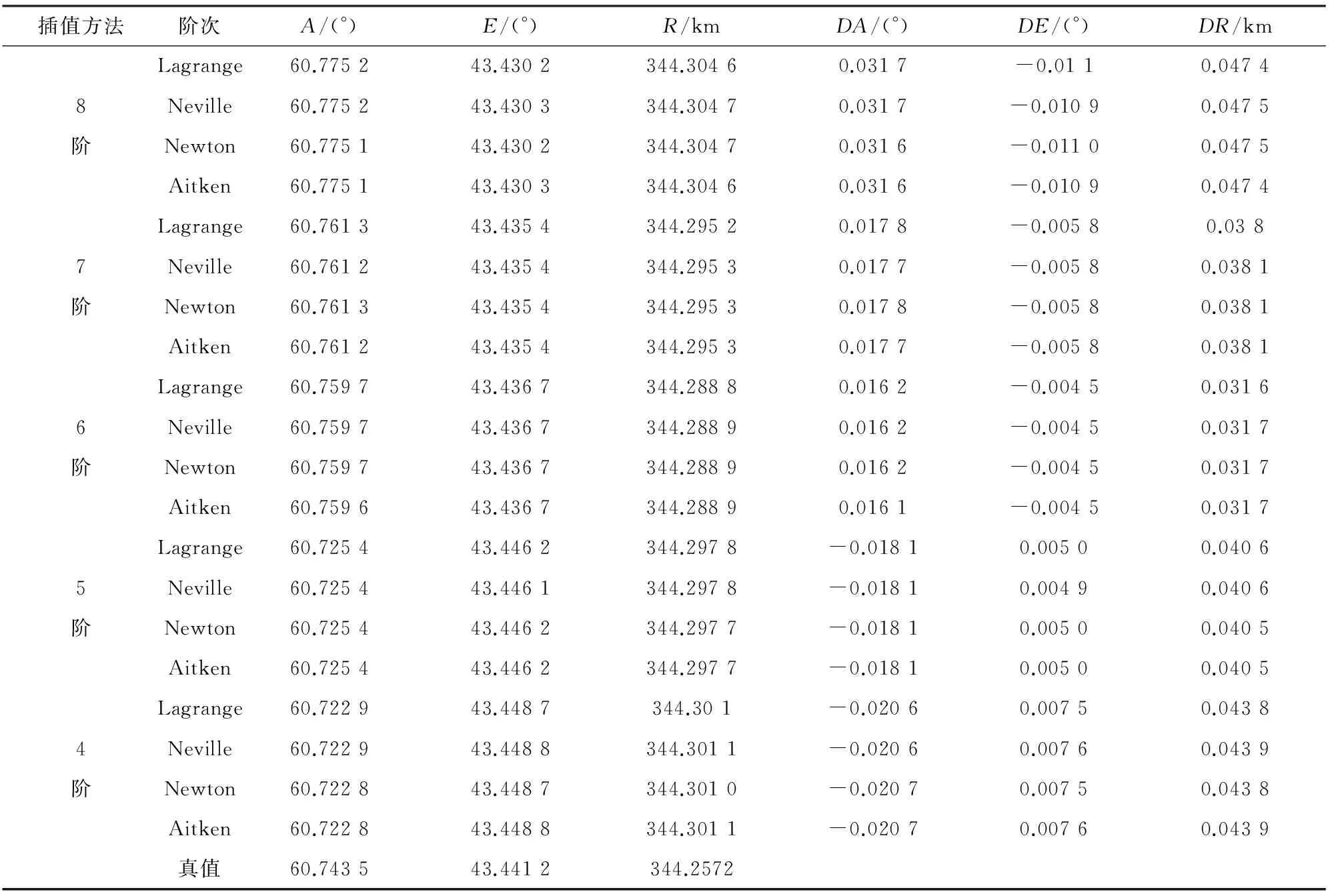
表4 插值点位于两端时的插值结果及其与真值的差值

通过表4，发现当插值点不在节点中央时，4种插值方法仍然表现出一致性，且都在6阶时达到精度最高，随着插值阶数的增大精度反而迅速降低。

通过表3和表4对比坐标插值结果和真值的差来看，发现插值点在中间时的精度高于插值点在两端的情况。对于插值阶数的选择，4种方法6阶的插值都可以达到要求，对于插值点不在节点中间的情况，无论采用哪种插值方法，相同阶数的插值精度总是比插值点在中央的情况要低，因此，在选择插值节点的时候，要尽量使插值点位于节点的中间，同时尽量选取偶数个节点。

3 结束语

由本文算例可以得到以下结论：

(1) Lagrange插值、Newton插值、Neville插值和Aitken插值用于内插程序引导数据，当插值阶数>6阶(包括6阶)且插值点位于节点中间时，插值结果表现出相当的一致性，插值精度可以满足测控设备要求。同时，更高阶的插值对于精度提高的贡献非常有限，反而增加插值的复杂程度。在内插时尽量选取节点数为偶数，使所求时刻尽可能位于节点的中间，插值的误差也最小；

(2) Lagrange插值的模型简单，是经典的插值方法。但是由于拉格朗日的基函数和每一个节点有关，使得原来的数据都不能利用，要重新计算，计算量大。当插值阶数较大时，Lagrange高次插值易产生所谓的龙格震荡现象，降低了多项式逼近的整体精确性；

(3) Aitken插值、Neville插值及Newton插值，其最后结果都基本相同。Neville插值模型简单、计算量小，没有龙格现象，程序实现方便灵活，易于增加和减少节点而不降低程序的效率，是一种较实用的内插方法。

[1] 鲁尽义.航天测控系统测角分系统[M].西安:中国电子科技集团公司第三十九研究所情报室,2008.

[2] 沈剑华.数值计算基础[M] .上海:同济大学出版社,1999.

[3] 李乃成,邓建中.数值计算方法[M].西安:西安交通大学出版社,2002.

[4] 易太义,陈道琦.数值分析[M].杭州:浙江大学出版社,1998.

[5] 田德宇,叶留青.Aitken-Neville-Newton插值法计算过程的等价性[J].河南科学,2007,25(6):885-887.

[6] 李庆扬,王能超,易大义.数值分析[M].北京: 清华大学出版社,2010.

[7] 陈启宏.m×n网函数插值及其Aitken逐次插值结构[J].苏州城建环保学院学报,1994(3):1-8.

[8] 刘迎春,林宝军,张晓坤.一种卫星精密星历的插值方法[J].飞行器测控学报,2004,23(4):43-46.

[9] 邱蕾,廖远琴,花向红.基于IGS精密星历的卫星坐标插值[J].测绘工程报,2008,17(4):15-18.

[10] 刘靖晔,刘立龙,宋元明,等.Aitken插值法插值GPS卫星精密坐标[J].地理空间信息,2011,9(6):75-76.

Measurement and Control Equipment Tracking Data Interpolation Method

PANG Yuefeng, WU Xiaodong, NIU Panfeng

(Department of Command and Control Station, Jiuquan Satellite Launch Center, Jiuquan 732750, China)

Interpolation of the converted azimuth and elevation angle is required in the measurement and control equipment, and the interpolation method should be as simple as possible without affecting the accuracy of interpolation. The commonly used methods of the Lagrange interpolation, Newton interpolation, Neville interpolation and Aitken interpolation are introduced, and the effects of the interpolation points on the interpolation results by these four methods are analyzed．The conclusion is obtained through the calculation of a practical example. Finally, the advantages and disadvantages of the four methods are discussed. It is concluded that the Neville algorithm is the best interpolation for guiding the tracking interpolation of space measurement and control equipment．

measurement and control equipment; guide tracking; Neville interpolation; Lagrange interpolation

2015- 12- 29

庞岳峰(1980-)，男，工程师。研究方向：测控地面站信号处理。

10.16180/j.cnki.issn1007-7820.2016.11.034

TP391.9

A

1007-7820(2016)11-118-04