一种基于最大度节点扩展的社区发现算法

赵卫绩,刘井莲,佟 良

(绥化学院 信息工程学院，黑龙江 绥化 152061)



一种基于最大度节点扩展的社区发现算法

赵卫绩,刘井莲,佟 良

(绥化学院 信息工程学院，黑龙江 绥化 152061)

针对星状社会网络，提出一种基于最大度节点扩展的社区发现算法.首先，计算网络中所有节点的度，选取节点的度大于等于阈值p的k个节点，以这k个节点为中心，与其各自的邻居节点形成k个分散的初始社区，删除重叠度高于给定阈值q的小社区.然后，对出现在这些初始社区中的重叠节点，提出一种近邻方法，通过计算这些节点到所在社区的距离，将其划分到距离最近的社区.对于k个初始社区外的节点，采用同样方法，将其划入到相应距离最近的社区.在真实网络数据集上进行了实验，实验结果表明，该方法能有效地处理初始社区内外边缘部分的不确定节点的划分问题，揭示出网络中存在的社区结构.相比经典的GN算法，该算法能得到更准确的划分结果，也具有更高的性能.

星状网络；社区发现；最大度节点

社会媒体网站的出现，不仅给人们提供了丰富的网络信息，也提供了新的社交手段.在社交网站上人们可以互相交流、分享信息、评价信息，这些操作的背后形成了丰富的关系数据.在这些数据背后，存在着大量的密集社区，社区发现能够揭示网络中的社区，已经成为社会网络分析中的一项重要研究.2002年，Girvan和Newman首次提出著名的GN算法[1]，通过计算网络中所有边的介数，并去除介数最大的边，重复该操作以获取网络中的社区结构，引发了国内外学者的广泛关注.文献[2，3]采用派系过滤思想，通过建立派系图，发现网络中的社区.文献[4]基于领域粗糙化，给出了一种启发式的社区发现方法.文献[5]基于图中的极大完全图扩展来挖掘网络中的社区结构.文献[6]将随机游走的蚁群算法应用于社区发现中.文献[7]基于传统密度聚类算法来发现层次社区结构.此外，还有采用图划分、拓扑式等方法的社区发现方法[8-10].Radicchi[11]对经典的GN算法进行了改进，采用边聚类系数代替边介数，算法运行效率相比GN算法有很大的提升.但该算法适合处理回路较多的复杂网络，不适合处理树状拓扑网络和星型拓扑网络.针对星状拓扑网络，本文提出一种基于最大度节点的社区发现算法.首先计算网络中所有节点的度，然后找出大于等于阈值p的top-k个节点，以这k个节点为中心，与其各自邻居节点形成k个分散的初始社区.对于初始社区交叉区域中的节点，提出一种近邻方法，通过计算交叉区域节点到其所在社区的距离，将其划分到距离最小的社区.对于k个初始社区外的节点，采用同样方法，将其划入到相应社区.在真实网络数据集上进行了测试，实验结果表明，该方法能够快速找到星状网络中的社区.

1 相关概念与公式

1.1 社会网络

“网络”是指由节点及节点之间的关系构成的集合.在社会学中，“社会网络”定义为行动者及其关系构成的集合[12].在社会网络分析中，常常用节点表示社会网络中的实体，边用于表示实体之间的关系.社会网络可以用图来描述，社会网络中的行动者是图中的节点，行动者之间的关系是图中的边.表示社会网络中的图，可以记作G=(V,E),V是节点集合，E是边集合，n=|V|表示图中节点的个数.

1.2 节点的度

节点vi的度用k(vi)表示，指与节点vi关联的边的数量.对于含有n个节点的图，节点度的最小值为0，是图中的孤立节点，不与任何节点相关联；节点度的最大值为n-1，与图中除了自身以外所有的节点都相关联.

1.3 重叠度

在社交网络中，存在大量的以度大的节点为中心形成的密集社区.为了衡量一个小社区在大社区中的包含程度，本文使用重叠度来衡量这一指标.设两个社区分别为Ci和Cj，则其重叠度Oij计算方法如下：

(1)

1.4 距离

对于社区间的边界节点及不在初始社区中的节点，为了衡量这些节点与哪个社区联系最紧密，本文使用一种改进的连接度方法来度量节点与社区之间的距离.设节点vi与初始社区Cj中的m个节点相连接，k(vi)是节点vi度，则节点vi到社区Cj的距离定义为：

dij=1-m/k(vi)

(2)

dij的值反映了一个节点vi与它的相邻社区之间的距离，如果vi与初始社区Cj中任何节点没有连接，则dij为1；节点vi与初始社区连接的节点越多，dij值越小.用m除以k(vi)，将距离规范化，使dij值分布[0,1].当dij值为0时，表示节点vi的邻居节点全在社区Cj中.

2 基于最大度节点扩展的社区发现算法

2.1 基本思想

在线社交网络中存在海量网络节点的同时，其形成的关系又往往是极度稀疏的.在这些社会网络中，常常存在着以某些节点与其邻居节点形成的密集社区结构.例如在明星粉丝团网络中，越受关注的明星具有越大的度，明星的度能够反映明星的活跃程度和被关注程度.针对此类网络，文献[13]提出了一种基于核心节点的复杂网络社区发现算法，该算法将相异度大的中心节点的集合组成核心节点集，然后采用相似性度量方法将网络中其他的节点划分到最相似的核心节点所在的社区.本文借鉴了该算法的思想，针对社会网络中存在以某些最大度节点为中心的密集区，提出一种新的社区发现算法.首先计算社会网络中各个节点的度，选取前top-k个节点为核心节点，将这k个核心节点与其各自的邻居节点生成k个分散的初始社区.然后对于初始社区交集的节点，基于连接度指标，将其划分到与其连接紧密的相应社区，对于初始社区外节点，采用同样方法将其划分到与其连接紧密的相应社区.该方法有效处理了初始社区不同程度的重叠问题和在初始社区外的节点的归属问题.

2.2 算法描述

(1)发现初始社区.首先计算图中每个节点的度，选取度大于等于阈值p的k个节点与其邻居节点集形成候选初始社区Ci.判断任意两个候选初始社区的重叠度，如果高于阈值q，则删除小社区，直到任意两个社区之间的重叠度均低于阈值q，形成初始社区划分.该方法保证了初始社区之间的重叠度低，提高了社区发现的稳定性.

算法1:发现初始社区输入:网络G=(V,E),度阈值p,初始社区重叠度阈值q;输出:初始社区划分C;方法:1)k=1;2)fori=1to|V|3)if(k(vi)≥p)4)Ck={vi}∪Γ(vi);5)k++;6)C=C1∪C2...∪Ck7)foranyCi,Cj∈C8)if(Oij>q)9)if|Ci|>|Cj|10)deleteCjfromC;11)else12)deleteCifromC;13)k--;14)returnC;

(2)处理初始社区间重叠节点和初始社区外结点的归属.首先，计算出现在两个及以上初始社区中出现的节点，构成重叠节点集B，然后采用公式(2)，计算重叠节点到对应重叠社区的距离，选择最近距离，将节点划到近邻社区内.具体算法如下：

算法2:形成最终社区划分输入:网络G=(V,E),初始社区C={C1,C2,…,Ck};输出:最终划分结果C={C1,C2,…,Ck};方法:1)B=Φ;2)fori=1to|V|3)ifviinmorethanonecommunities4)B=B∪{vi};5)forj=1to|B|6)calculatethedistancefromvjtoinitialcommunitieswhichvjbelongsto;7)addvjtothecommunitywhichhasminimumdistance;

对于初始社区外节点采用5)～7)同样的方法处理，将其划入到与其距离最小的社区内.

2.3 算法示例与分析

为了测试本文提出算法的有效性，在图1(a)所示数据集上[13]，验证了本文提出算法的有效性.网络中的节点及边，如图1(a)所示.

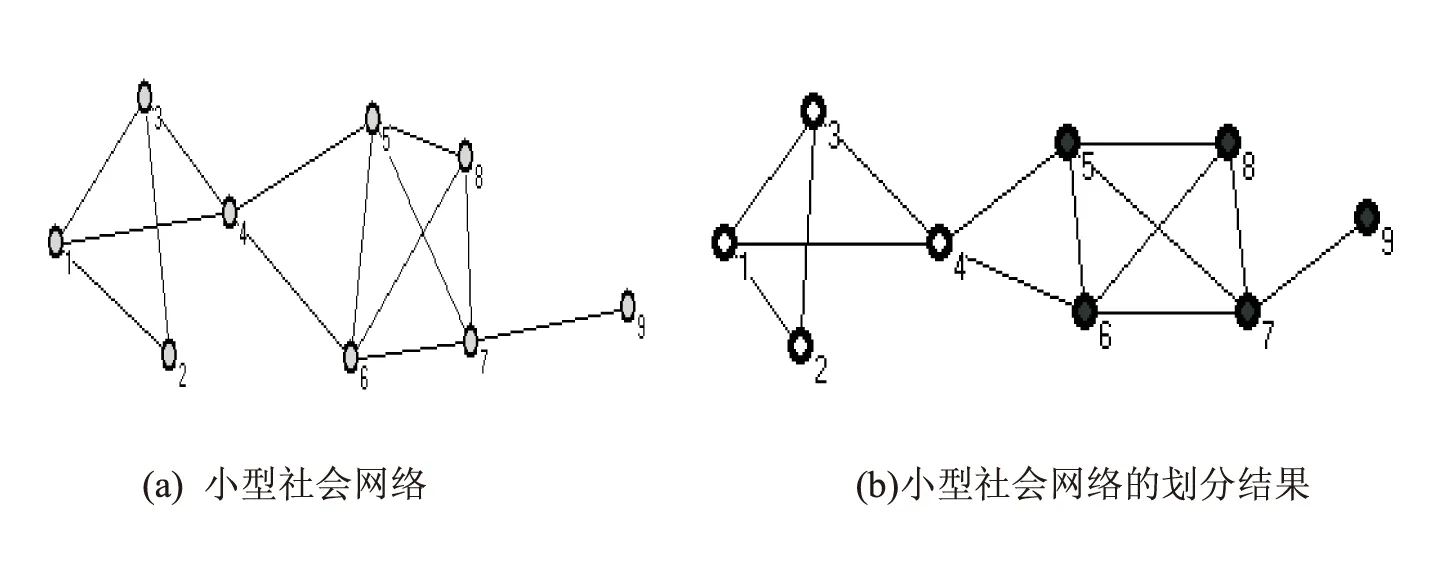
图1 一个小型社会网络及其划分结果

计算步骤：第1步，形成初始社区：设p=4,q=0.75,选取节点的度大于等于p的节点集合为{4,5,6,7}，形成4个初始社区，这四个节点与其各自的邻居节点形成的初始社区分别为C1={4,1,3,5,6}，C2={5,4,6,7,8}，C3={6,4,5,7,8}，C4={7,5,6,8,9}.第2步，处理初始社区的重叠问题，逐一计算各个社区的重叠度，其中C4与C2和C3的重叠度0.8，大于等于q，则保留节点数目较多的C4，删除C2和C3，形成最终的初始社区：C1={4,1,3,5,6}和C4={7,5,6,8,9}.第3步，处理社区交集间节点的归属问题，C1∩C4={5,6}，而节点5只与社区C1中的节点4连接，与C4中的节点6、7、8都连接，因此节点5距离C4最近，划分到社区C4中，将节点5从社区C1中删除.同理节点6距离C4社区最近，划分到社区C4中，将它从社区C1删除.处理完交叉节点后的社区为：C1={4,1,3}和C4={7,5,6,8,9}.第4步，处理初始社区外节点的归属.初始社区外的只有节点2，采用步骤3中的方法，由于节点2只与C1中节点有连接，与C4中节点没有连接，所以节点2划分到C1中.最终形成的两个社区分别为{1,2,3,4}和{5,6,7,8,9}，与实际相符.社区划分结果如图1(b)所示.

3 实验

本文采用经典数据集“美国大学空手道俱乐部成员间的社会关系”[14]来测试本文算法的准确性.该俱乐部成员的社会关系网具体如图2(a)所示，图中包含34个节点，78条边，其中每个节点表示该俱乐部的一个成员，节点间的边表示两个成员之间经常在一起参加俱乐部活动.该俱乐部由于主管节点34和教练节点1之间发生分歧而分裂成以两个节点为核心的俱乐部.

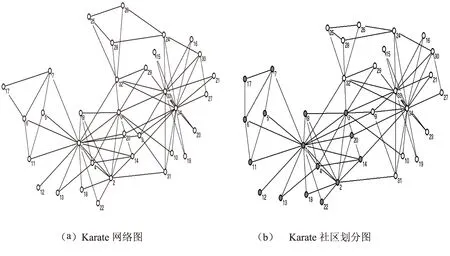
图2 Karate网络图及其划分结果

采用本文方法，首先度最大的节点1和34，与其邻接节点构成的初始社区为：A={1,2,3,4,5,6,7,8,9,11,12,13,14,18,20,22,32}和B={9,10,14,15,16,19,20,21,23,24,27,28,29,30,31,32,33,34}.其中A和B的交集为{9,14,20,32}，节点9分别与社区A中节点1、3相连接，与B中节点31,33,34相连，所以节点9到初始社区B距离最小.同理节点14、20划分到社区A，节点32划分到社区B.

对于初始社区A和B之外的节点{17，25，26}，采用同样方法，由于节点17只与初始社区A中节点6，7连接，因此节点17划分到社区A中；同理，节点25只与B中节点连接，划分到社区B，节点26只与社区B相连，划分到社区B.因此最终形成两个社区：以节点1为中心16个节点组成的社区{1,2,3,4,5,6,7,8,11,12,13,14,17,18,20,22}和以节点34为中心18个节点组成的社区{9,10,15,16,19,20,21,23,24,25,26,27,29,30,31,32,33,34}.具体如图2(b)所示.

从实验结果来看，本文提出的基于最大度节点的社区发现算法，能够得到与实际相符的社区结构.而经典的GN算法[1]，将节点3错误划分到以34为中心的社区B.对比GN算法，本文算法在星状社会网络中能够得到更准确的划分结果.

4 总结

社区发现是社会网络分析中一项重要的研究工作，目前已经在生物领域、在全球传染病病毒传播上和恐怖主义活动分析、微博、电子商务中等多个领域发挥了重要作用.本文针对社会网络分析中常常存在以度大节点为中心的密集区，提出一种基于最大度节点的社区发现算法.该算法通过选取度大节点与其邻居节点形成多个分散的初始社区，对初始社区间重叠部分节点和初始社区外节点采用连接度指标，实现复杂社会网络社区的合理划分.相比经典的GN算法，能得到更加准确的划分结果.

[1]M.Girvan,M E J.Newman. Community structure in social and biological networks[C].Proceedings of the National Academy of Sciences，2002,99(12):7821-7826.

[2]G.Palla,I.Derenyi,T.Farkas et al..Uncovering the overlapping community structure of complex networks in nature and society[J].Nature，2005,435(7043):814-818.

[3]T S.Evans.Clique graphs and overlapping communities [J].Journal of Statistical Mechanics Theory and Experiment，2010,2010(3):257-265.

[4]张泽华,苗夺谦,钱进.邻域粗糙化的启发式重叠社区扩张方法[J].计算机学报，2013,36(10):2078-2086.

[5]刘井莲,赵卫绩,佟良.一种基于极大完全图扩展的社区挖掘算法[J].河南科学，2015,33(12):2140-2145.

[6]金弟,杨博,刘杰,刘大有,何东晓.复杂网络族结构探测-基于随机游走的蚁群算法[J].软件学报，2012,23(3):451-464.

[7]林旺群,卢风顺,丁兆云,吴泉源,周斌,贾焰.基于带权图的层次化社区并行计算方法[J].软件学报，2012,23(6):1517-1530.

[8]黄健斌,孙鹤立,DustinBORTNER,刘亚光.从链接密度遍历序列中挖掘网络社区的层次结构[J].软件学报,2011,22(5):951-961.

[9]张忠元.基于字典学习的网络社K结构探测算法[J].中国科学:信息科学，2011,41(11):1343-1355.

[10]淦文燕,赫南,李德毅,王建民.一种基于拓扑势的网络社区发现方法[J].软件学报，2009,20(8):2241-2254.

[11]F.Radicchi,C.Castellano,F.Cecconi,V.Loreto,D.Parisi.Defining and identifying communities in networks[J].Proceedings of the National Academy of Sciences of the United States of America.2004,101(9):2658-2663.

[12]S.Wasserman,K.Faust.社会网络分析：方法与应用[M].陈禹，等译.北京：中国人民大学出版社，2012:26,69.

[13]牛冬冬,陈鸿昶,金鑫,刘力雄.基于核心节点的复杂网络社区划分算法[J].计算机工程与设计,2013(12):4089-4093.

[14]W.W.Zachary.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1977,33(4):452-473.

(责任编辑:王前)

A Novel Community Detection Algorithm Based on Maximal-degree Nodes Expansion

ZHAO Wei-ji, LIU Jing-lian, TONG Liang

(SchoolofInformationEngineering,SuihuaUniversity,Suihua,Heilongjiang152061,China)

For detecting community structure in star networks, a novel algorithm based on maximal-degree nodes expansion is proposed. Firstly, the degrees of all nodes in a network is computed. The top-k nodes as the center nodes whose degrees are bigger than or equal to threshold p, the top-k nodes and their neighbor nodes form k initial communities are found out. The small communities whose overlapping with other communities are larger than a predefined threshold q is deleted. Then, a close neighbor method, which adds the node to a community with which it has a minimum distance is proposed for dealing with the overlapping nodes among initial communities. Using the same method, add the nodes outside the k initial communities to the corresponding community with which they have minimum distances. Finally, our algorithm on a famous real-word network is evaluated. The result demonstrates that our algorithm can deal with overlapping nodes and nodes outside the initial communities effectively, and can uncover the community structure in networks. Compared with GN algorithm, our algorithm has a higher accuracy and better performance.

star network; community detection; maximal-degree node

10.13877/j.cnki.cn22-1284.2016.08.024

2016-06-06

绥化市2015年科技计划项目“基于社区发现的社交网络分析与研究”；绥化学院青年基金资助项目(KQ1301002)；黑龙江省大学生创新创业训练计划项目(201610236014)

赵卫绩，男，山东青岛人,讲师.

TP311

A

1008-7974(2016)04-0072-04