基于供求分析法对出租车资源配置的研究

黄 瑞，朱家明，陈浩杰，方佳佳

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)



基于供求分析法对出租车资源配置的研究

黄 瑞1，朱家明2，陈浩杰2，方佳佳2

(1.安徽财经大学 金融学院，安徽 蚌埠 233030；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

针对北京市“互联网+”时代的出租车资源配置，使用统计分析、变异系数等方法，分别从司机和乘客两个角度分析得到供给与需求函数，建立供求比、空载率、打车成功率三个指标并构建综合评价模型分析不同时空出租车资源的“供求匹配”程度，研究表明，北京市市区出租车资源“供求匹配”程度除了在中午时段之外均不高，早晚高峰以及二、四环均存在打车难现象．最后对主要公司的出租车补贴方案进行了定性分析与定量评价，据此给出相应的建议．

互联网+；出租车资源；供求分析；综合评价

出租车是市民日常出行的重要交通工具之一，“打车难”也是人们关注的一个社会热点问题．在移动网络快速发展的大趋势以及打车难的市场现状的共同作用下，互联网+打车的创新模式应运而生．从美国的优步到我国的滴滴打车，多家公司依托互联网建立的打车软件服务平台，使得司机与乘客之间的匹配方式由完全随机到预约安排，缓解了部分信息不对称问题．同时各家公司为开拓市场推出多种补贴方案，但由于发展时间较短，补贴方案和盈利模式等方面存在缺陷．因此，对出租车市场的资源配置和补贴方案的优化设计具有重要意义．

1 基本假设

为了便于解决问题,提出以下假设:①假设打车软件的人群范围足够广，故打车软件服务平台推出的补贴政策对出租车市场能够产生直接影响；②假设出租车司机掌握出车与否的决定权；③假设所有司机和乘客均为理性人；④假设当指标选定后，其他因素造成的影响忽略不计；⑤打车软件服务平台为社会福利服务，最主要的目的在于解决“打车难”问题；⑥出租车数量有限，故供给量达到一定程度不能再增加．

2 不同时空出租车资源的“供求匹配”程度

2.1 指标的确定

从出租车司机角度分析得到出租车市场的供给函数

Qs=mai(1-μi)(i=1,2,3…)

其中，Qs表示出租车实际供给量;m表示北京市某一地区(或某一时段)出租车平均出行总量;ai表示北京市某一地区(或某一时间)平均每辆出租车在第i个时段(或地点)的出行次数;μi表示北京市某一地区(或某一时段)每辆出租车在第i个时段(或地点)的空载率．

从乘客角度分析得到出租车市场的需求函数

Qd=nibikω(i=1,2,3…)

其中，Qd表示乘客实际需求量;ni表示北京市某一地区(或某一时段)在第i个时段(或地点)的出行人口量;bi表示北京市某一地区(或某一时段)出行人口平均每人在第i个时段(或地点)的出行次数;k表示北京市某一地区(或某一时段)出行人口乘出租车出行占所有出行方式的比例;ω表示北京市某一地区(或某一时段)每辆出租车平均每次载客人数．

由供给函数与需求函数得到出租车市场的供给量与需求量，求得供求比．由于供求比只能从宏观上反映供求量的关系，因此考虑到从乘客和司机的角度添加相应的指标即打车成功率和空载率，来对匹配程度进行衡量．定义打车成功率为平均每个乘客期望等车时间与平均每个乘客实际等车时间之比．

2.2 综合评价模型

采用变异系数法确定权重并建立相对隶属度矩阵．首先，明确各指标的属性，用I1、I2、I3分别表示固定型、效益型和成本型指标，其中供求比属于固定型指标，空载率属于成本型指标，打车成功率属于效益性指标．其次，针对上述三个指标建立相应的隶属度矩阵，通过无量纲化，将矩阵各元素转化为效益型或成本型指标；最后，将处理后的矩阵组成相对隶属度矩阵．

指标隶属度矩阵R的建立

其中，i=1时,uij∈I1；i=2时，uij∈I2；i=3时，uij∈I3；j表示不同时间段或地区；rij是隶属度矩阵R的组成元素．

综合评价各个指标数据，得到衡量出租车资源“供求匹配”程度的供求匹配指数SD．

SD=W·R=

“供求匹配”程度等级，如表1所示．

表1 “供求匹配”程度等级

2.3 结果分析

用MATLAB编程求得不同时空北京市出租车资源的“供求匹配”指数如表2、表3所示．

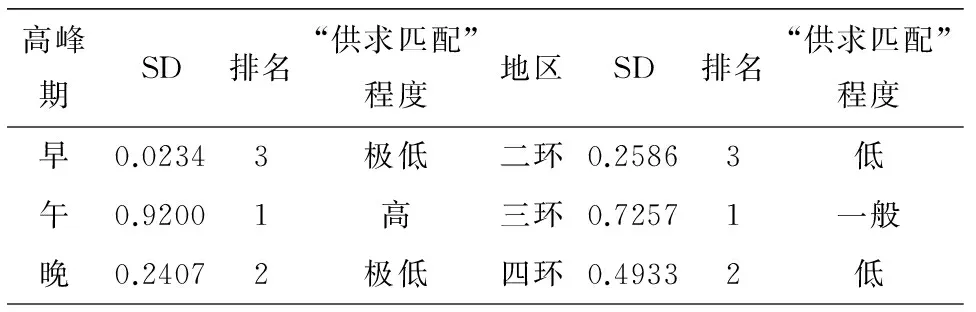
表2 不同时段和地区北京市市区的出租车资源“供求匹配”程度

由表2可知，北京市市区出租车资源“供求匹配”程度除了在中午时段之外均不高．早晚高峰以及二、四环均存在打车难现象．

3 打车软件的补贴方案分析

3.1 定性分析

快的打车与滴滴打车的补贴方案如表3所示．

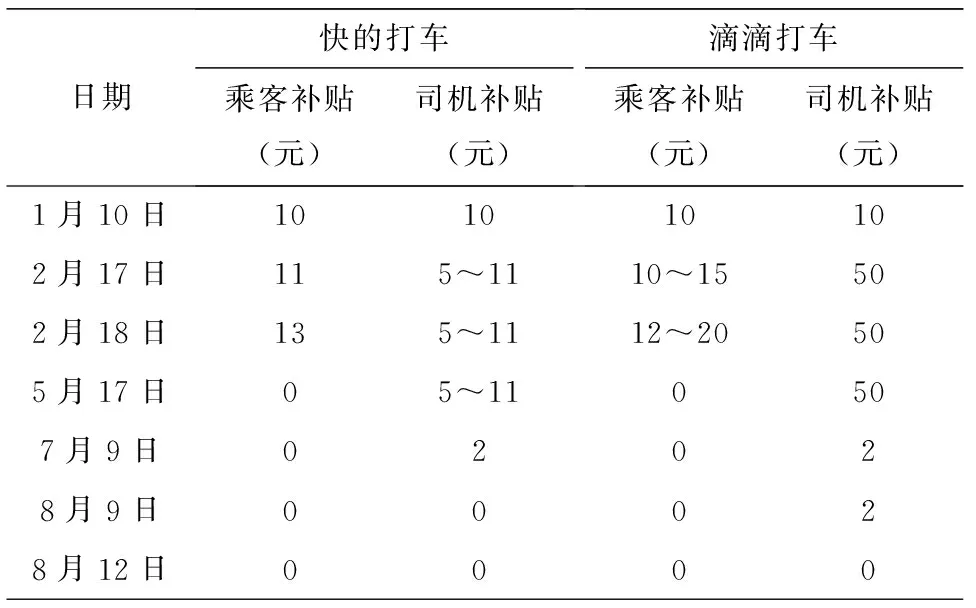
表3 快的打车与滴滴打车的补贴方案

(1)乘客对出租车的需求量Qd.Douglas在1972年提出一个出租车市场的集合模型

其中，Qd是乘客对出租车的需求量；P是出租车单次出行的费用；T是平均等候时间；d0是出租车空驶里程．

空驶里程可以作为打车成功性的一种度量，在道路总长度和出租车数量不变时，平均等候时间与出租车空驶里程数成严格反比，且不受其他任何参数的影响．同一时空，平均候车时间为一定值，此时，乘客对出租车的需求量仅与出租车单次出行的费用有关．

(2)司机对出租车的供给量Qs.对一个出租车司机而言，追求的是利润，即盈利额与成本之差，利润(R)大于零，选择出车．因此，得到关于出租车供给量Qs的供给模型

C=f(U+V)

其中,U代表出租车实载时间；V代表出租车空驶时间；C代表出租车运营的成本．

研究表明，补贴方案之对出租车司机和乘客同时进行返现补贴：对于出租车司机而言，相当于成本减少，故供给量增加；对于乘客而言，本身使用打车软件的乘客都是具有乘车需求的乘客，所以需求量并不会有明显的增加，同时补贴返现只针对于接单成功情况，接单成功的供给方与需求方相互匹配，考虑到需求与供给的净值，故同样的需求情况下，供给方增加，空驶率也随之增加，故打车的难度将降低．补贴方案之只对出租车司机进行补贴：对于出租车司机而言，由于补贴仅针对接单成功的情况，所以部分的供给量与对应的需求量互相匹配；对于使用软件的乘客而言，打车成功率较高；在供给量一定的情况下，定点供给增加，空驶率下降，对于其他乘客而言，打车难的现象不仅未得到缓解反而被加剧．

3.2 定量分析

取表1中北京市区不同时段的数据进行研究，从而分析各公司的出租车补贴方案是否对“缓解打车难”有帮助．各公司出租车补贴后各指标增加或减少的比例以及相应计算出的指标值如表4所示．

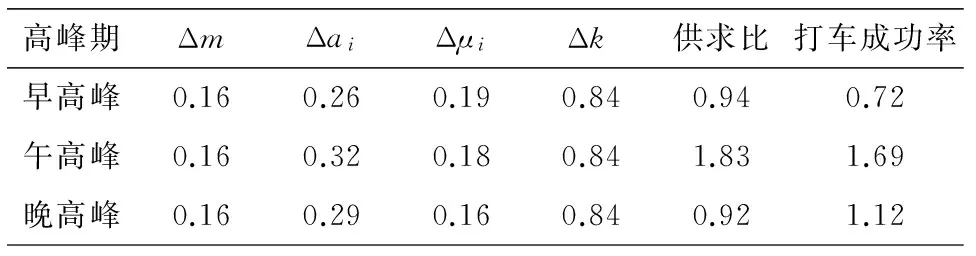
表4 补贴后北京市区不同时间各指标改变的比例及计算的指标值

将表中数据代入综合评价模型解得各公司出租车补贴后北京市区不同时刻的“供求匹配”指数和补贴前的“供求匹配”指数见表5．

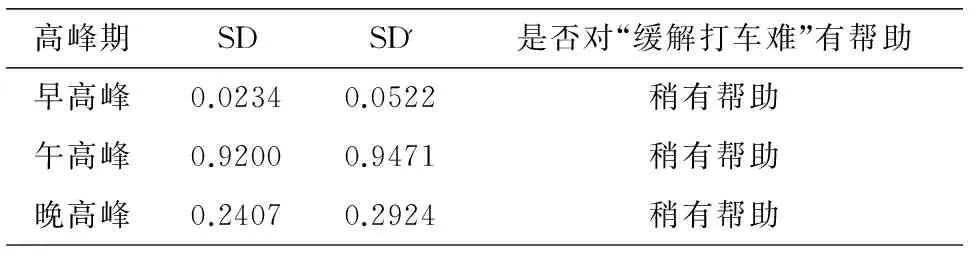
表5 补贴前后的北京市区不同时间的“供求匹配”指数

由表5可知，各公司出租车补贴方案对使用打车软件的打车乘客来说，缓解了打车难问题．

4 补贴方案设计

4.1 宏观比较分析

首先对宏观情况进行定性分析．春夏秋冬四季、高峰期与闲暇期出租车供给率与需求率如图1、图2所示，其中需求率表示乘客乘出租车出行占所有出行方式的比例，供给率表示出租车出行量占所有交通方式的比例．

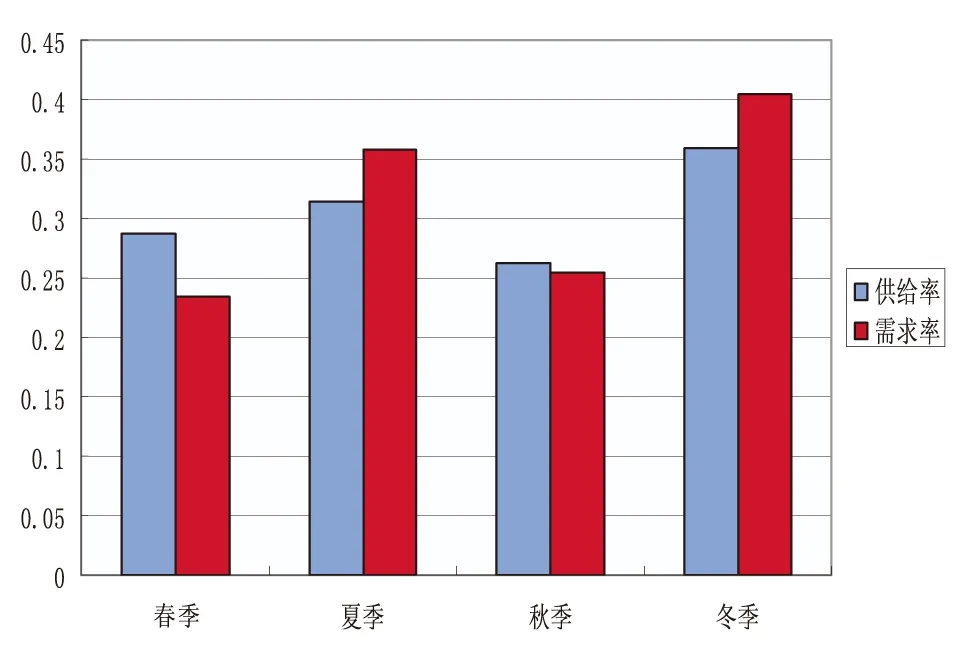
图1 出租车供给率与需求率四季对比

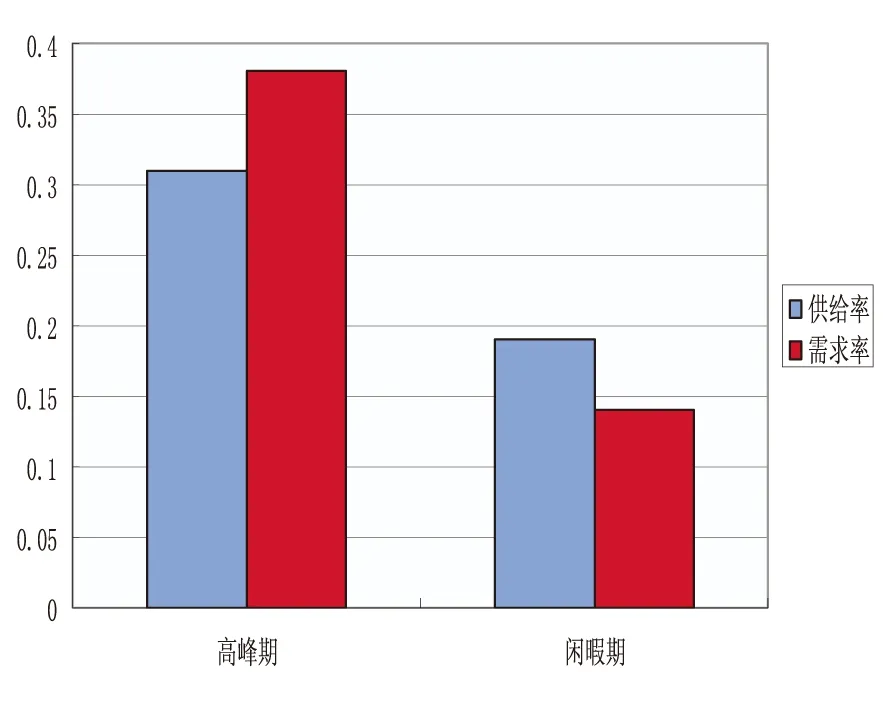
图2 高峰期、闲暇期出租车供给率与需求率对比

由统计分析可以看出，春季、秋季的供给率高于需求率，这与日常的直观认识一致：春、秋季大多时间天气凉爽，乘客考虑出行成本，一般会偏向于选择公交车、地铁等公共交通工具，因而需求率下降，而夏、冬季极端天气较多，一般而言，乘客更偏向于选择出租车，节约时间成本，同时，由于出租车大多只上交强险，只保第三方，因此在恶劣天气情形下，出车风险大，相对收益低，因此出租车供给率下降；高峰期人流量较大，对出租车的需求量大，然而高峰期道路交通堵塞，车辆运转速度低，对司机而言利润降低，出租车供给量下降，体现出需求与供给的矛盾，打车较难；而在非高峰期，由于道路通畅，换乘率较高，单位时间平均载客次数高于高峰期，供给率较高，出租车空驶现象严重，但此时由于没有时间成本的限制，乘客可以选择的出行交通工具多样，对出租车的需求率较低．

综上，一般而言，春、秋季和非高峰期出租车的供给率高于需求率；夏、冬季和高峰期出租车的供给率低于需求率，“打车难”现象更为严重．故下文主要针对夏、冬季和高峰期进行分析．

4.2 改进的供需模型

引入经济学中供给弹性与需求弹性概念，针对高峰期出租车市场进行分析．其中，供给弹性指供给量相对价格变化作出的反应程度．衡量当其他所有影响销售计划的因素保持不变时，一种产品供给量对其价格变动的反应程度．此处，出租车的供给可看作一种服务产品．供给弹性系数es的计算公式为

需求弹性在此处指需求价格弹性，表示在一定时期内一种商品的需求量变动对于该商品的价格变动的反应程度．需求弹性系数ed的计算公式为

基于假设，对2.2中得到的出租车的供给函数作出相应的改进，由于出租车数量有限，故供给量不能无限增加：当司机预期收入大于预期的出车总成本时，出租车的供给量逐渐提高，当出车的边际成本与边际收益相等时，利润最大，此时供给弹性最大，之后随着单次出行费用P的增加，出租车供给函数增加速度变慢，最终趋于稳定不再随着P的增加而增加．高峰期时出租车市场供求分析图如图3所示，其中Qd为简化的需求函数曲线，Qs为改进后的供给曲线．

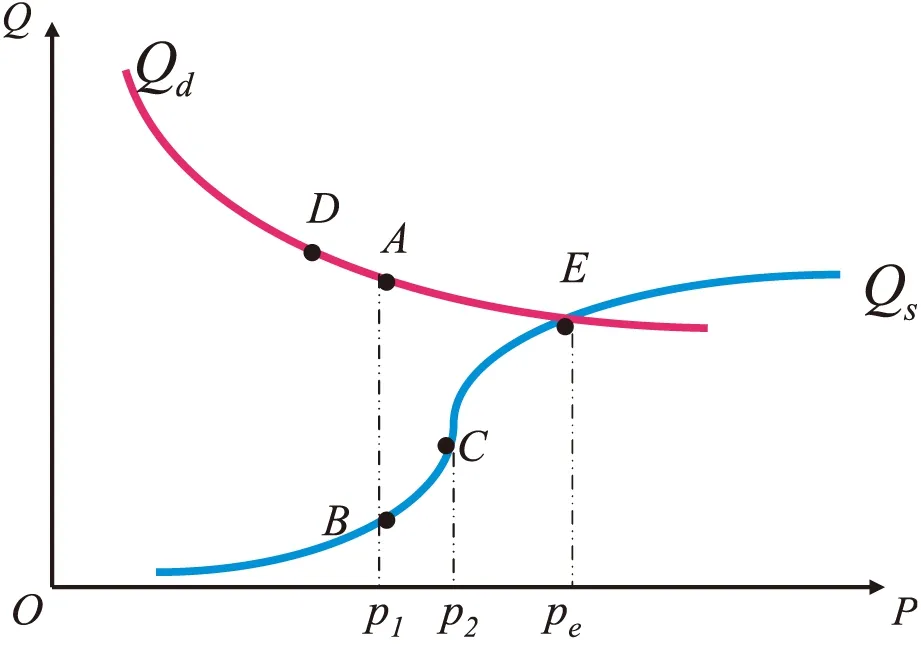
图3 高峰期出租车市场供求分析

4.3 结果分析

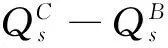
在乘车高峰期，用情境体验法思考，作为乘客的直观感受是：在需要打车却打不到车的情况下，甚至会有加价打车的想法，需求量并未有明显的降低，故需求弹性并不高，甚至可以说需求是偏刚性的；作为司机，高峰期堵车现象严重，换乘率低，相同时间内平均载客次数减少，只有在预期利润大于预期成本的情况下，司机才会有出车的意愿，从实际情况上看，出租车供给量明显增加，供给弹性大于需求弹性．冬、夏季打车难情况与高峰期基本类似，此处不再赘述．

综上所述，以最小的成本缓解打车难问题，较好地选择是只对出租车司机予以一定金额的补贴．所以构建新的补贴方案为：夏、冬季和高峰期：不对乘客补贴，只对出租车司机进行补贴．

5 结论

针对出租车资源的配置优化问题，本文构建出供求模型并通过综合评价模型得到的供求平衡指数，对于衡量一个城市供求匹配程度以及对交通系统中出租车市场供给的调节调度具有重要意义．在出租车市场集合模型的基础上结合现实情况进行改进，并创新性地提供了经济学中边际与弹性分析方法，考虑气候、时段等因素，提出进行非对称补贴的建议．在实际调研获取得到数据的基础上，以最大程度的供求均衡为目标，对于打车软件平台定量计算补贴具体金额具有重要意义．

[1]安雨康.基于供需关系探究北京出租车行业打车难问题[J].现代径济信息,2013(5):306.

[2]柳丽娜,陈艳艳,张文阁.北京市出租车乘客需求预测模型研究[J].交通标准化,2010(13):89-92.

[3]杨桂元.数学建模[M].上海:上海财经大学出版社,2015.

[4]司守奎.数学建模算法与应用[M].北京:国防工业出版社,2011.

[5]Douglas G W.Price regulation and optimal service standards:The taxicab industry[J].Journal of Transport Economics and Policy,1972,20:116-127.

[6]高鸿业.西方经济学(微观部分)[M].北京:中国人民大学出版社,2001.

[7]De vany A S. Capacity Utilization under Alternative Regulatory Constraints:An Analysis of Taxi Markets[J].Journal of Political Economy,1975,83:83-94.

(责任编辑:陈衍峰)

10.13877/j.cnki.cn22-1284.2016.08.012

2015-11-20

国家自然科学基金“基于数据包络分析的环境效率分析评价方法及其应用研究”(11301001);安徽财经大学教研项目“数学建模竞赛引领大学生科研创新的研究”(acjyzd201429);国家级大学生创新项目“医保欺诈行为的主动发现”(201510378153)

黄瑞,女,安徽淮北人,安徽财经大学金融学院在读．

朱家明,安徽泗县人,副教授．

O245

A

1008-7974(2016)04-0037-04