具有瓦片翼的旋转子弹气动特性数值研究

2016-12-19赵养正吕鸿鹰向玉伟

弹箭与制导学报 2016年4期

关键词：攻角升力子弹

赵养正,吕鸿鹰,向玉伟

(中国兵器工业第203研究所,西安 710065)

具有瓦片翼的旋转子弹气动特性数值研究

赵养正,吕鸿鹰,向玉伟

(中国兵器工业第203研究所,西安 710065)

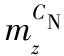
瓦片翼;高阻力;旋转子弹;数值模拟

0 引言

末修弹药是常规弹药制导化的重要部分。当末修子弹抛出母弹弹体后,瓦片尾翼打开,不但对末修子弹进行减速减旋,而且起到稳定子弹姿态的作用。弹翼采用瓦片翼形状是典型的阻力翼,可以增大子弹飞行阻力,同时迅速降低子弹的转速,从而保证末修子弹在一定的速度和转速下搜索目标。目前对旋转弹箭的气动特性的研究较多,文献[1]通过试验的方法研究了平头圆柱体带四片升力翼的子弹的滚转阻尼特性,文献[2-5]通过准静态数值的方法研究了旋转状态下的动导数,文献[6]研究了一种异形卷弧翼弹旋转状态下的气动特性,但研究这种具有瓦片翼子弹的气动特性的文献较少,因此通过数值方法研究具有瓦片翼子弹的气动性能意义重大。

1 模型

模型结构为台阶型弹体+3片瓦面型尾翼(见图1)。此气动外形具有特殊的气动特性,即升力小、阻力大,可使弹体速度、转速快速降低,增大弹道落角,短时间内达到最终子弹稳定工作状态。

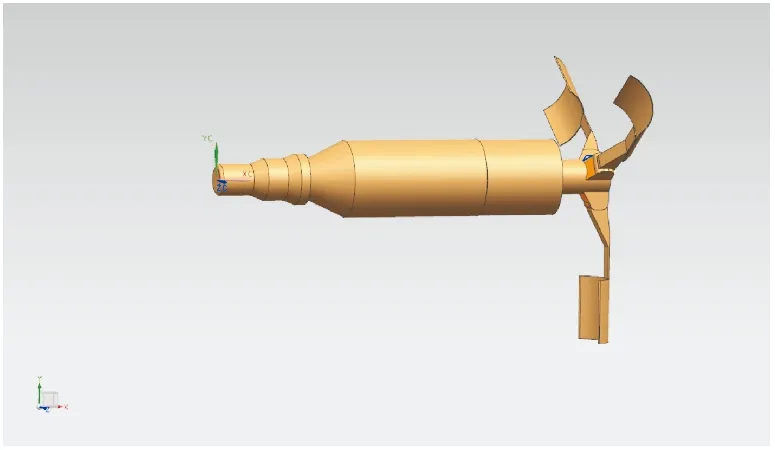
图1 模型示意图

2 数值方法

2.1 计算方法

文中使用CFD软件cfx进行数值计算。具体计算方法为:结合SST湍流模型,并采用有限体积中心差分格式对三维雷诺平均Navier-Stokes方程进行求解。由于模型是旋转的,因此采用了旋转坐标系[1],坐标系固定在子弹体上,随子弹一起以固定的角速度旋转。入口边界采用速度和温度;出口边界采用静压和温度;远场边界采用无粘滑移边界墙;壁面边界采用无滑移壁面条件。

2.2 计算网格

外场采用四面体网格,附面层采用三棱柱形网格。模型的表面网格和附面层网格见图2和图3。

图2 表面网格

图3 附面层网格

2.3 计算条件

1)静态计算条件

马赫数:0.2～1.5;攻角:0°～30°;

2)动态计算条件

马赫数:0.2～0.8;攻角:0°～12°;

转速:5～15 r/s。

3 结果与讨论

文中对静态和旋转状态的气动特性进行了研究,并对静态的计算结果和实验结果进行了比较分析。

3.1 静态结果

由图4可看出:正攻角时,升力系数为负值,升力系数随攻角变化为负线性的。此变化规律与常规弹刚好相反,因为常规弹的法向力大,轴向力小,而此弹的法向力小(见图5),轴向力大(见图6),虽然法向力正攻角时为正值,但坐标系转化时要减去大的轴向力分量,导致升力在正攻角时为负值。

体轴系转化为风轴系的公式为:

CD=CAcosα+CNsinα

CL=CNcosα-CAsinα

其中:α为攻角;CA、CN为体轴系的轴向力系数和法向力系数;CD、CL为风轴系的阻力系数和升力系数。

从图7的阻力系数曲线可以看出:在所研究的攻角范围内,阻力系数比常规弹箭大得多,大约是标准弹箭模型(CBM)零升阻力的10倍,而且阻力随攻角变化较小;同时阻力随马赫数的变化也小。因此这类弹的阻力受攻角的影响很小,阻力平稳。

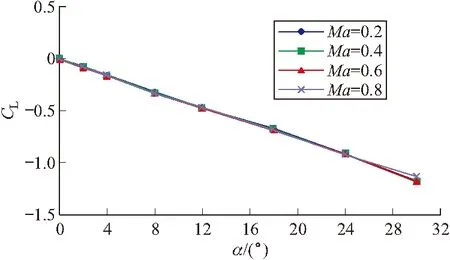
图4 升力系数随攻角的变化曲线

图5 法向力系数随攻角的变化曲线

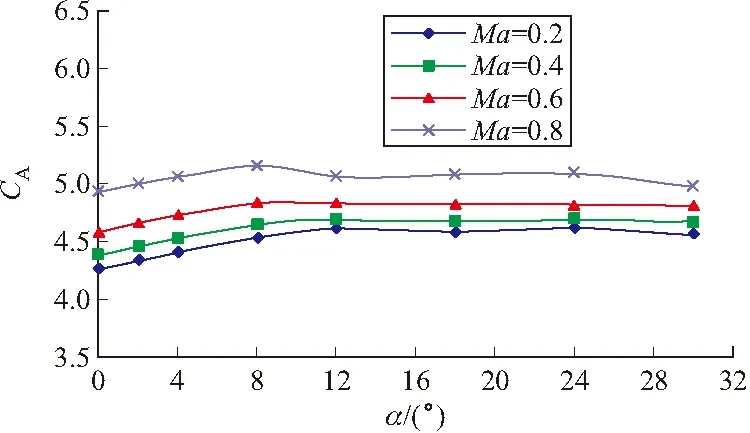
图6 轴向力系数随攻角的变化曲线

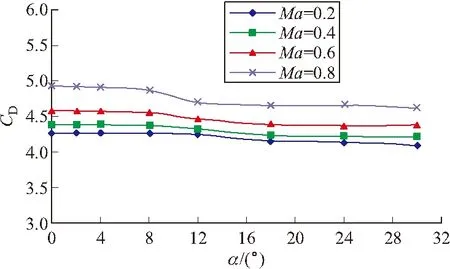
图7 阻力系数随攻角的变化曲线

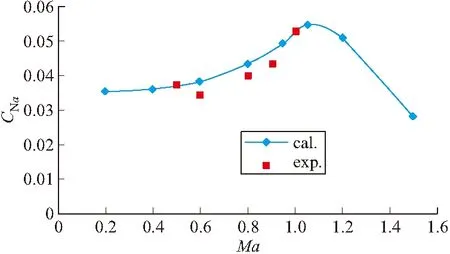
图8 法向力系数导数随马赫数的变化曲线

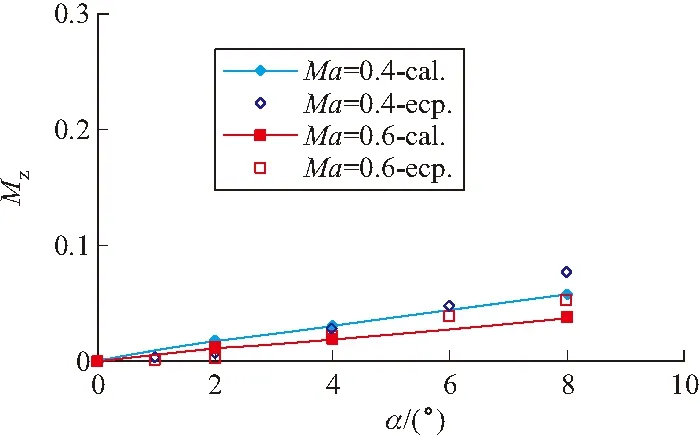
图9 俯仰力矩系数随攻角的变化曲线

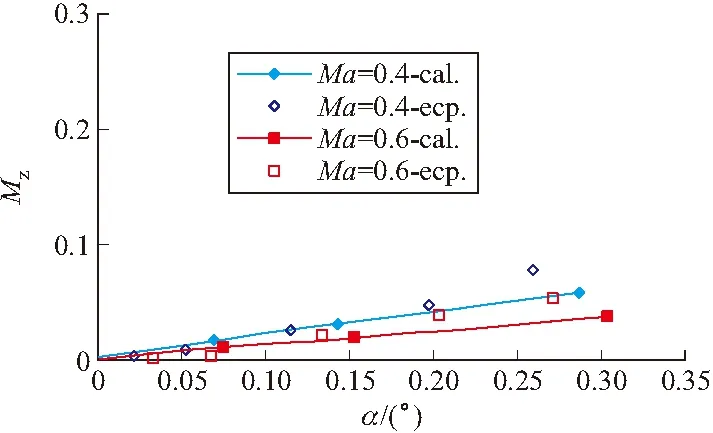
图10 俯仰力矩系数随法向力系数的变化曲线

3.2 旋转状态结果

在旋转状态结果中,将静态结果作为转速n=0 r/s处理,从图11(a)可以看出随着攻角的增大,在不同转速下法向力系数出现了分化,在7 r/s以下法向力是随着转速的提高逐渐减小;然而,当转速处于10 r/s以上时,法向力变为负值,转速越高,法向力绝对值越小,从图11(b)可以看出法向力系数随转速的增大,经历了先减小后增大的过程,在8 r/s附近不同攻角下的法向力系数接近零,是变化的转折点。比较图12和图13可以看出,转速为5 r/s时(见图12),下半表面的压力大于上半表面的压力,因此法向力为正;转速为10 r/s时(见图13),下半表面的压力小于上半表面的压力,因此法向力为负,这是由于转速增加,使近表面的流场压力分布发生改变造成的。

图14为俯仰力矩系数(对质心)随攻角及转速的变化曲线,从图14(a)可以看出不同转速下的俯仰力矩系数较小,尤其是转速为15 r/s时俯仰力矩系数最接近零,同一攻角下转速为10 r/s时的俯仰力矩系数最大,而转速为15 r/s时的俯仰力矩系数最小。从图14(b)可以看出同一攻角下,攻角小于6°和转速小于等于7 r/s时俯仰力矩的变化较小;在攻角大于6°和转速大于7 r/s时俯仰力矩的变化较大。

图11 法向力系数随攻角及转速的变化曲线(Ma=0.2)

图12 模型法向力分布(r=5 r/s,Ma=0.2,α=6°)

图13 模型法向力分布(n=10 r/s,Ma=0.2,α=6°)

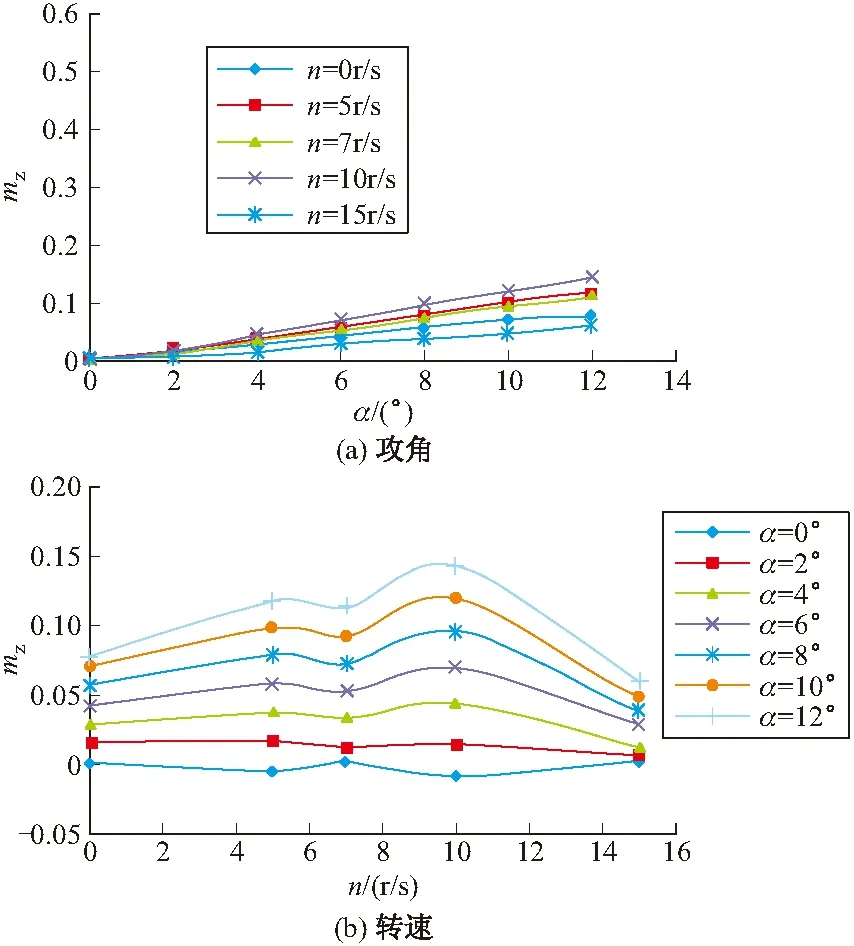
图14 俯仰力矩系数随攻角及转速的变化曲线(Ma=0.2)

图15 俯仰力矩系数随法向力系数的变化曲线(Ma=0.2)

3.3 静稳定性

3.4 动稳定性

下面通过火箭外弹道学方法用导弹稳定性的判定准则对旋转子弹的静、动稳定性加以判定。

1)静稳定条件

陀螺稳定因子[7]:

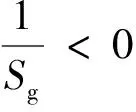
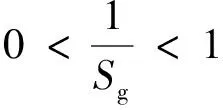
2)动稳定条件

动稳定因子[8]:

慢圆运动稳定条件:

通过对该弹Ma=0.2时动稳定性的计算表明,Sd<0,为慢圆运动。高速旋转状态下n=15 r/s时,该弹满足慢圆运动稳定条件;当n≤10 r/s时,该弹为陀螺不稳定,动不稳定,因此该弹在较高速旋转状态是动稳定的。

4 结论

文中通过数值计算和实验方法研究了具有瓦片翼子弹的气动特性,并通过对比分析得出如下结论:

1)采用文中的数值方法计算的气动参数实用、可靠,与试验结果一致性非常好。

2)与常规弹箭不同,此弹的法向力小,轴向力大,虽然法向力在正攻角时为正值,但正攻角时,升力系数为负值,升力系数随攻角变化为负线性关系。

3)该弹赋予不同的旋转速度后出现了法向力正负分化的现象。

4)在小攻角和低转速下旋转运动对俯仰力矩的影响较小;在大攻角和高转速下旋转运动对俯仰力矩的影响较大。

5)在子弹低速旋转时仍然可以应用旋转弹的静态参数来判定子弹的稳定性,但高速时就不能应用。

6)Ma=0.2时,该弹要通过高速旋转的陀螺效应才能实现动稳定。

[1] 赵养正, 蒋胜矩, 党明利, 等. 旋转弹体及减旋片滚转阻尼数值模拟 [J]. 兵工学报, 2015, 36(7): 1176-1180.

[2] 丁则胜, 刘亚飞, 徐琴, 等. 弹体及减旋片滚转阻尼实验研究 [J]. 弹道学报, 2001, 13(1): 62-65.

[3] 邓帆, 陈少松, 陶钢. 带栅格翼导弹超声速阶段滚转阻尼导数的数值研究 [J]. 空气动力学学报, 2012, 30(2): 151-156.

[4] MACHAEL A P, LAWRENCE L G. steady-state computation of constant rotational rate dynamic stability derivatives: AIAA 2000-4321 [R]. 2000.

[5] DESPIRITO J, SILTON S I, WEINACHT P. Navier-Stokes predictions of dynamic stability derivatives-evaluation of steady-state methods: Maryland, USA: ARL-TR-4605 [R]. 2008.

[6] 金华, 戴金海, 吴蓓蓓. 一种异形卷弧翼弹气动特性的数值模拟 [J]. 弹箭与制导学报, 2006, 26(3): 168-171.

[7] 吴甲生. 雷娟棉. 制导兵器气动布局与气动特性 [M]. 北京: 国防工业出版社, 2008: 299-306.

[8] MURPHY Charles H. Free flight motion of symmetric missiles: BRL Report No.1216 [R]. 1963.

The Aerodynamic Performance Simulation of a Spinning Projectile with Tile Wings

ZHAO Yangzheng,LYU Hongying,XIANG Yuwei

(No.203 Research Institute of China Ordnance Inductries, Xi’an 710065, China)