火箭弹发射试验锥形运动稳定性分析

颉凯平,畅仲仁,郑书娥

(中国空空导弹研究院,河南洛阳 471009)



火箭弹发射试验锥形运动稳定性分析

颉凯平,畅仲仁,郑书娥

(中国空空导弹研究院,河南洛阳 471009)

由于舵翼面安装误差、发动机推力偏心及各种随机扰动的综合影响,火箭弹有可能出现较大幅度并发散的锥形运动导致试验失败。文中通过锥形运动的机理分析,提出当纵横向运动频率接近或交叉且弹体振荡幅度较大时才会出现锥形运动发散。仿真结果表明,通过火箭弹纵横向运动频率及振荡幅度的数学仿真,可给出舵翼面安装误差及发动机推力偏心的控制要求。

火箭弹;锥形运动;频率;振荡幅度

0 引言

为考核某型导弹发动机工作性能和弹架分离安全性,需要进行火箭弹地面发射试验。由于火箭弹舵翼面安装误差、发动机推力偏心及随机干扰的综合影响,火箭弹有可能出现较大幅度并发散的锥形运动导致试验失败。20世纪60年代,美国的奈特霍克探空火箭在50次的飞行试验中,曾有近20次出现了发散的锥形运动[1]。西班牙的140 mm火箭弹在28次飞行试验中出现了9次锥形运动[2]。国内在某型制导火箭弹飞行试验中,也出现了锥形运动发散问题[3]。

文中通过火箭弹锥形运动的机理分析,提出火箭弹出现较大幅度并发散的锥形运动应具备的条件,基于火箭弹飞行稳定性的仿真计算,给出舵翼面安装误差、发动机推力偏心的控制要求。

1 锥形运动机理分析

锥形运动是火箭弹动不稳定的一种表现形式,锥形运动发生时,火箭弹除绕自身纵轴的自旋转运动外,还表现出弹体纵轴绕速度方向的旋转运动,如图1所示,其中ζ为章动角,x4为火箭弹的瞬时速度方向,xc为弹体纵轴方向[4]。

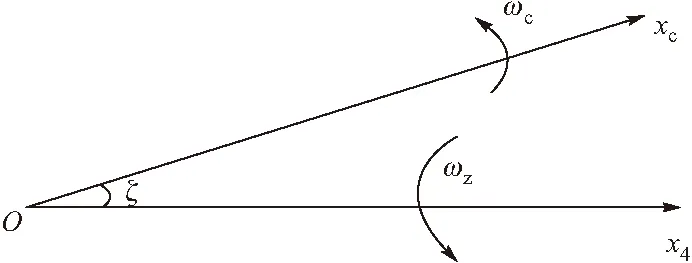
图1 锥形运动示意图

1.1 弹体纵向运动平面运动模型

弹体纵向平面短周期运动扰动方程可简化为[5-6]:

(1)

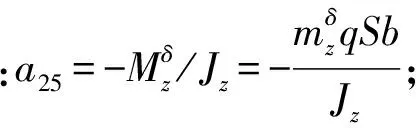
舵偏角到攻角之间的传递函数:

(2)

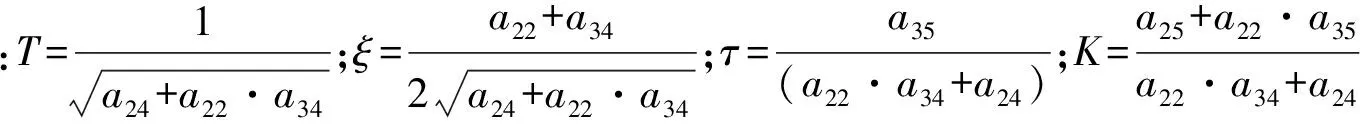
由于a22·a34+a24≫a35,因此τ≈0。于是将式(2)简化为:

(3)

1.2 锥形运动分析

式(3)中取K=1.3、T=0.05、ξ=0.2,当俯仰等效舵偏角为20＇,若弹体不滚转,攻角变化见图2;若弹体滚转速度为2 Hz,即滚转周期为T=1/(4π),攻角变化见图3。可见,弹体无滚转时,攻角很快收敛,而当弹体有滚转运动时,攻角出现周期性振荡。

采用上面的数学模型,通过统计仿真,得出只有当纵横向运动频率接近或交叉时,会出现锥形运动。随着静稳定恢复力矩的影响,锥形运动会逐渐收敛,但若振荡幅度太大,则会使火箭弹锥形运动发散。

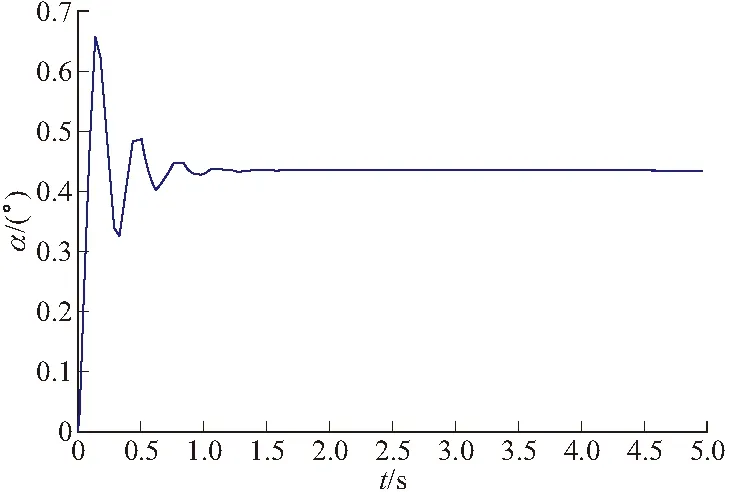
图2 攻角变化(无滚转)

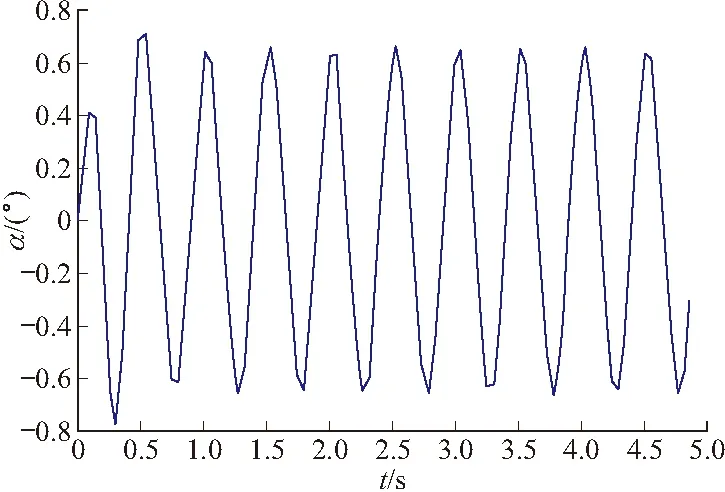
图3 攻角变化(有滚转)

2 纵横向运动频率分析

选取不同的滚转等效舵偏角(简称Dx),火箭弹纵横向运动频率的仿真结果见图4。

图4 火箭弹纵横向运动频率的仿真结果

可见,当横滚等效舵偏角在10＇ 以内时,纵横向运动频率不会出现接近或交叉现象;而当横滚等效舵偏角为10＇ 时,火箭弹纵横向运动频率在弹道飞行中段较为接近。因此,舵翼面安装误差导致的横滚等效舵偏角应控制在10＇ 以内。

3 振荡幅度分析

选取不同的俯仰等效舵偏角(简称Dy)及发动机推力偏心(简称Py)进行火箭弹弹道仿真。步骤如下:

1)取横滚等效舵偏角为控制要求最大值,即Dx=10＇,先叠加俯仰等效舵偏角Dy,依次取5＇,10＇,15＇;

2)取上一步计算得到的俯仰等效舵偏角控制要求最大值,再叠加发动机推力偏心Py,依次取5＇,10＇,15＇。

限于篇幅,仅列出Dx=10＇,Dy=12＇,Py=10＇ 条件下的仿真结果,见图5。

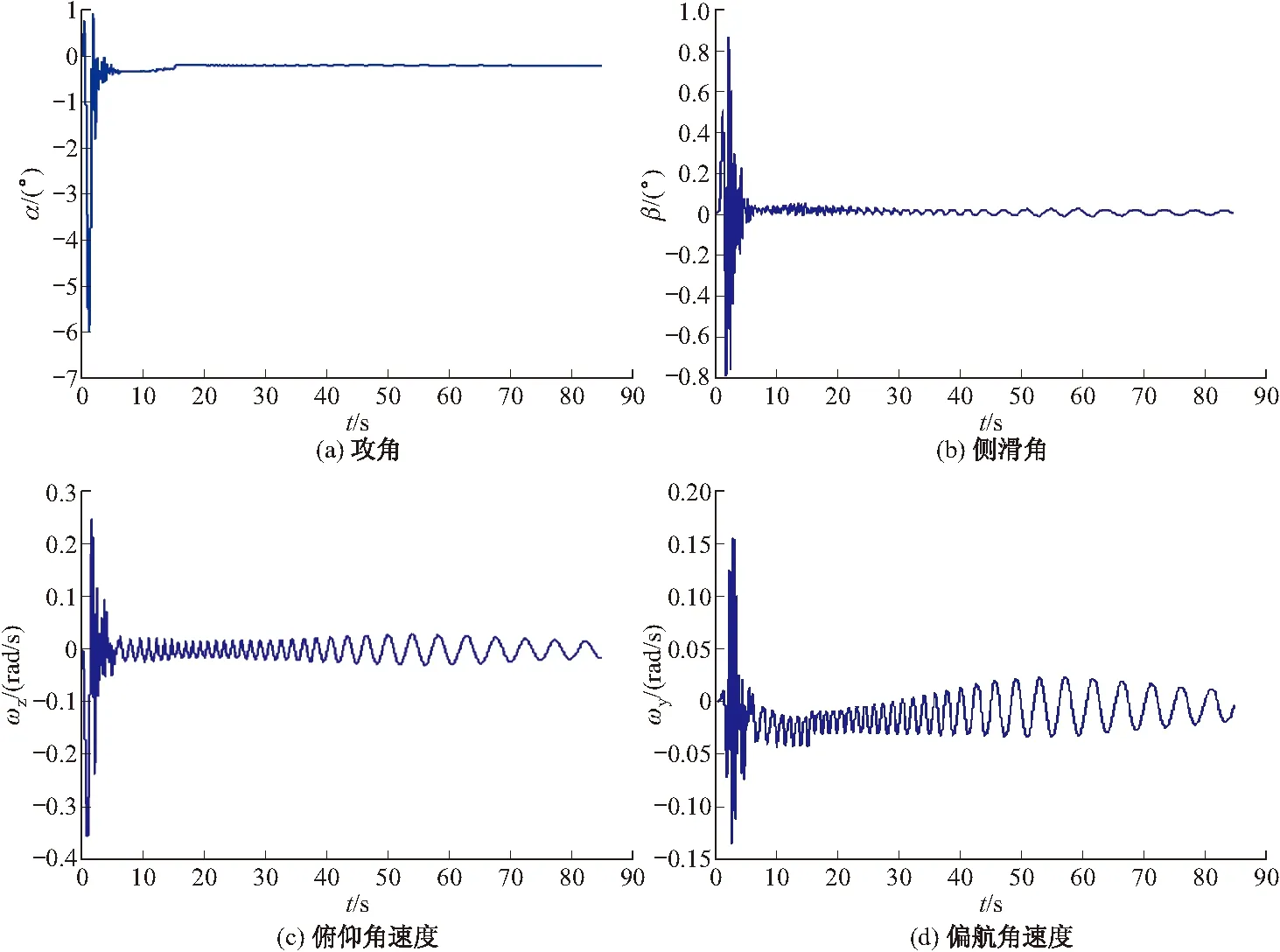
图5 仿真结果

结果表明:

1)即使Dx取最大误差控制要求10＇,叠加Dy在15＇ 以内时,攻角、侧滑角的振荡幅度很小,表明火箭弹的滚转运动消弱了Dy对弹体运动的影响。Dy对弹体稳定性影响较小,相比Dx的控制精度要求可降低,控制在12＇ 以内即可。

2)由于火箭弹初始段静稳定恢复力矩小,Py较大时,会产生较大的偏转力矩使火箭弹飞行初始段弹体姿态发生较大变化,进而产生火箭弹落点散布,且增加了锥形运动发散的可能性,因此,应控制发动机推力偏心在一定误差范围内。

4 结论

火箭弹锥形运动发散需要两个条件:一是纵横向运动频率接近或交叉;二是纵横向频率接近或交叉时弹体振荡幅度较大。基于火箭弹纵横向运动频率及振荡幅度两个步骤的分析,可给出火箭弹舵翼面安装误差和发动机推力偏心的控制要求。

[1] CURRY W H, REED J F. Measurement of magnus effects on a sounding rocket model in a supersionic wind tunnel: AIAA 66-754 [R]. 1966.

[2] MOROTE L G. Stability analysis and flight trials of a clipped wrap around fin configuration: AIAA 2004-5055 [R]. 2004.

[3] 张成, 杨树兴. 一种滚转导弹飞行姿态的获取方法 [J]. 北京理工大学学报, 2004, 24(6): 481-485.

[4] 赵良玉, 杨树兴. 卷弧翼火箭弹圆锥运动收敛速度计算方法 [J]. 固体火箭技术, 2009, 32(1): 15-19.

[5] 李新国, 方群. 有翼导弹飞行动力学 [M]. 西安: 西北工业大学出版社, 2005: 206.

[6] 钱杏方, 林瑞雄, 赵亚男. 导弹飞行力学 [M]. 北京: 北京理工大学出版社, 2000: 176.

Stability Analysis of Conical Motion for Rocket Launching Test

XIE Kaiping,CHANG Zhongren,ZHENG Shu’e

(China Airborne Missile Academy, Henan Luoyang 471009, China)

Due to influences of installation error of rudder and wing, engine thrust misalignment and random disturbance, conical motion with large amplitude and divergence may occur to rocket projectile, which causes test failure. In this paper, mechanism of conical motion was analyzed. When longitudinal and transverse movement frequencies close or cross and amplitude of missile body is larger, the conical motion divergence is presented. Simulation results show that through mathematical simulation of longitudinal and transverse movement frequencies and oscillation amplitude of rocket projectile, the control requirements of wing surface mounting error and engine thrust misalignment are given.

rocket projectiles; conical motion; frequency; oscillation amplitude

2015-08-06

颉凯平(1986-),男,甘肃甘谷人,工程师,研究方向:飞行器总体设计。

TJ760

A