低温贮箱隔热层打磨机器人的动力学仿真分析

◎黄顺舟 王力 祁佩 张崇印

低温贮箱隔热层打磨机器人的动力学仿真分析

◎黄顺舟 王力 祁佩 张崇印

在低温贮箱隔热层机器人柔性自动打磨过程中，合理控制机器人末端执行器运动轨迹可有效保证打磨质量，因此需对打磨机器人进行动力学分析。本文采用广义坐标形式的牛顿-欧拉方法对空间一般串联机器人建立多体系统动力学方程，将六个关节的驱动角位移作为机器人系统的广义坐标,根据打磨机器人各活动构件几何和物理参数，在驱动力给定的情况下，对打磨机器人动力学正问题进行了仿真分析。仿真结果表明打磨机末端执行器走了一条非预期的波动的路径。因此，为了获得较好的打磨质量，提供有效的机器人动力学建模与仿真方法是非常有意义的，同时本文动力学建模方法也为打磨机器人的主动控制算法提供了一定的基础。

某型号低温贮箱外壁喷需喷涂一层聚氨酯泡沫塑料（PU）作为隔热材料（见图1），聚氨酯泡沫塑料喷涂后表面凹凸不平（见图2）。考虑到减重、外形表面美观、隔热效果等因素，需进行打磨加工处理，打磨精度要求±2mm。

打磨亦称磨削，是指用磨料、磨具切除工件上多余材料的加工方法，即在一定程度上去除前道工序加工所形成的凸层和痕迹，保证工件满足形状、尺寸、粗糙度等方面要求。

图1　喷涂有隔热材料的低温贮箱

图2　低温贮箱隔热层喷涂后表面凹凸不平

贮箱箱底结构比较复杂，主要体现为：箱底为椭球形曲面结构；箱底在制造过程中存在焊接变形，因而并非规则的曲面结构；箱底有很多法兰等凸起物；箱底边缘为短壳结构。箱底的结构复杂性导致其隔热层打磨难度较大，也较难实现自动化打磨，此外隔热层打磨过程中不能碰撞法兰等凸起物，否则易导致贮箱损坏而报废。目前，该型箱底仍采用人工手动打磨方法，不仅加工周期长，生产效率低，精度差，产品质量稳定性差，而且人工劳动强度大，作业环境也差。

由于实际产品结构复杂且制造偏差较大难以直接采用基于理论模型的自动专机打磨，需研究基于机器人的柔性自动打磨技术（如图3所示），以满足不同类型尺寸贮箱打磨的加工要求，同时保证隔热层打磨质量及其稳定性。在机器人实际打磨前，也有必要分析机器人打磨运动过程的动力学性能，以便对机器人进行运动控制。

针对机器人动力学的建模方法主要有：牛顿-欧拉方法、第二类拉格朗日方程和虚功原理。牛顿-欧拉方法以矢量力学为基础，单个刚性构件为建模对象，采用笛卡尔坐标描述多个构件组成的系统的位姿，联立运动副约束方程，组成系统动力学方程，由于积分变量为全部的笛卡尔坐标，计算量较大。第二类拉格朗日方程以分析力学为基础，从能量角度出发，对于少自由度系统，求出每时每刻各活动构件的动能和势能，然后对广义变量求偏导数，推导过程程式化程度高，然而当系统自由度增加时，计算量急剧上升，过程变得尤为繁琐，并且无法得到关节的理想约束力。虚功原理处理问题较为简洁，处理动力学逆问题效率较高，但计算动力学响应时同样无法直接得到约束力。

本文采用广义坐标形式的牛顿-欧拉方法（Schiehlen方法）对空间一般串联机器人建立多体系统动力学方程。本文结合打磨机器人关节驱动的运动特征，将各关节的驱动角位移作为广义坐标，各连杆的笛卡尔坐标通过齐次坐标变换矩阵的方法依次推导得到，所以各连杆的位姿可以转换为以广义变量表示的形式，然后对时间分别求一次和两次导数代入牛顿方程和欧拉方程，联立用矩阵形式求解。若求解动力学正问题，不需要关节理想约束力，可以用虚功原理将理想约束力和虚位移相乘得零，得到较为简化的动力学方程。本文根据构件几何和物理参数，在驱动力恒定的情况下，对打磨机器人动力学正问题进行了仿真分析。

图3　低温贮箱隔热层打磨机器人

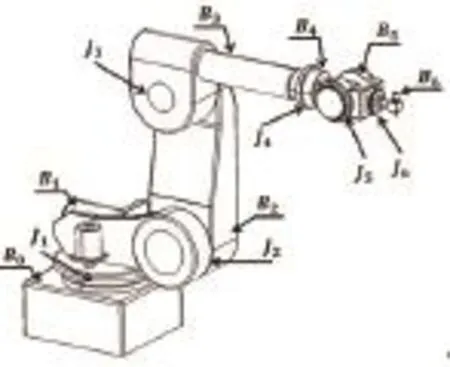
图4　打磨机器人机械结构示意图

打磨机器人

低温贮箱隔热层打磨机器人（如图4所示）是一个六个转动副铰接而成的串联机械臂。一般情况下，串联机械臂逆运动学问题难以求解且不唯一，但对于机器人运动控制来说，这是一个基本问题。本文打磨机器人是一台KUKA公司的210kg工业机器人，其运动学逆解则并不困难，因为其机构构型设计较为巧妙，即末端连续的三个转动副（即四轴、五轴和六轴）的轴线是交于空间一个共同点。工业机器人的运动学逆解求解过程大致如下：已知机器人末端执行器的位置和姿态（以下简称“位姿”），容易计算上述共同点在机器人世界坐标系（亦可称“笛卡尔坐标系”）中的位置坐标值，接着通过联立三个三元方程可计算机器人从基座开始的三个转动副（依次为一轴、二轴和三轴）的角位移，最后也通过求解三变量方程组可计算机器人四轴、五轴和六轴的角位移。

图5　打磨机器人各连杆连体坐标系

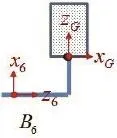
图6　工具连体坐标系

打磨机器人动力学建模

本节采用Schiehlen多体动力学方法分析机器人操作手的动力学正问题。首先建立运动学模型，其次建立动力学模型。

运动学分析

为了描述各刚体在空间的位置和姿态，在打磨机器人各连杆上建立连体坐标系，如图5所示。齐次坐标变换矩阵用来表征两个不同坐标系之间的相对位置和姿态。通常地，从机器人一个构件连体基到另一个构件连体基的变换关系可由一个4×4的矩阵T来描述。假设矩阵i-1Ti是从构件i-1到构件i的变换矩阵，那么机器人相邻构件间的六个变换矩阵可表达如下：

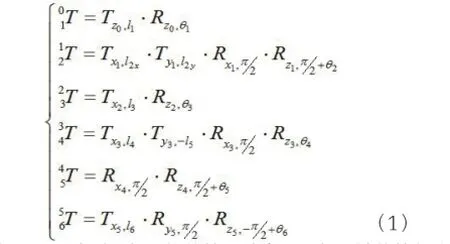
其中：li和θi分别是每个构件的尺寸常量和每个关节的角位移变量；带有右下标的矩阵T和矩阵R分别为在前一个坐标系中描述的移动矩阵和转动矩阵。例如，式中的0T1是指前一个坐标系（即第0个坐标系，描述为“x0y0z0”）沿着z0轴方向平移l1长度，然后绕着z0轴方向转动θ1角度，至此第0个坐标系和第1个坐标系重合。其余类似。因此，从基坐标系0到末端坐标系6的总变换如下表示：

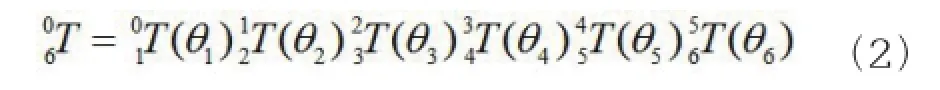
式中i-1Ti(θi)是一个以θi为变量的矩阵函数。

机器人末端工具固定在刚体6上，同样地，工具的连体坐标系如图6所示。

刚体6坐标系到工具坐标系的变换是一个常数矩阵，表示如下

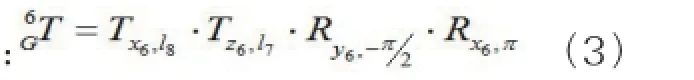
所以打磨机器人末端工具在基坐标系下的位置和姿态可以表示如下：通常，末端执行器的轨迹是给定的，所以矩阵0TG为已知。为了获得动力学仿真的初始条件，首先计算六个关节的初始角位移。本文我们关注末端三关节的相交点J5。如果末端工具的位置已知，那么矢量在基坐标系里的描述能计算得到。所以J5的位置表示如下：

式中r→表示在基坐标系下的矢量。

此外，J5的位置也可以由如下方程获得：

所以，三个未知数θ1、θ2和θ3可以通过如下方程组解出：

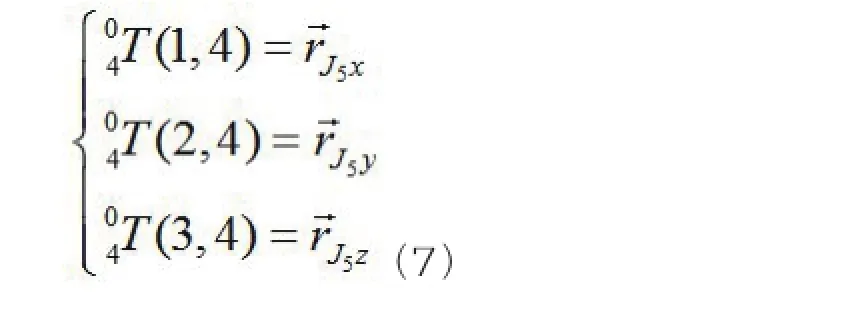
式中T(I,j)表示矩阵T的第I行第j列的元素。

此外，其余三个未知数θ4、θ5和θ6可以通过如下方程解出：

假设Ci是第i个连杆的质心，其位置表示如下：

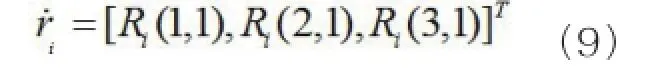
用方向余弦表示角速度，各连杆在局部坐标系下的角速度描述如下：

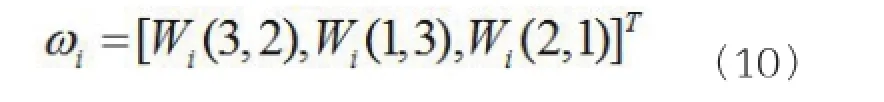
动力学分析

动力学分析旨在研究力与运动之间的关系。本文采用Schiehlen多体动力学建模方法。每个刚性连杆建立相应的牛顿欧拉方程，如式所示。

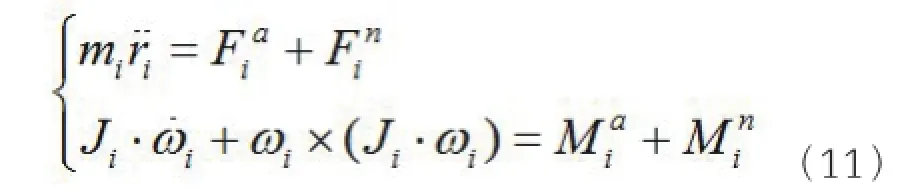
式中mi和Ji分别为各连杆的质量和惯量，aFi和aMi分别是主动力和主动力矩，nFi和nMi分别是约束力和约束力矩。

一般地，各连杆的位置和角速度分别能表示成广义变量或者广义变量对时间的导数的函数，如式14,15所示：

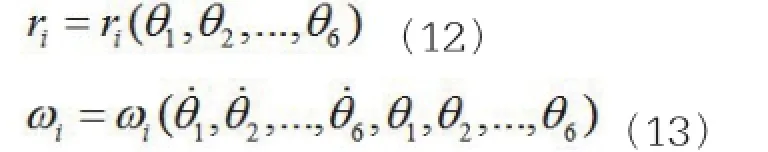
考虑虚功原理，约束力的虚功等于零。在本文的打磨机器人动力学分析中，在各主动力作用下机器人末端执行器的运动轨迹是所需要计算的，而约束力是不需要的。所以Schiehlen描述的动力学方程表示如下：

式中：θi和τi分别是各关节的角位移和驱动扭矩，Fr和irRP分别是作用在末端执行器上的外部工作阻力和局部坐标系中工作阻力作用点坐标矢量。

为了便于在Matlab/Simulink中搭建仿真数值模型，我们将式变化如下：

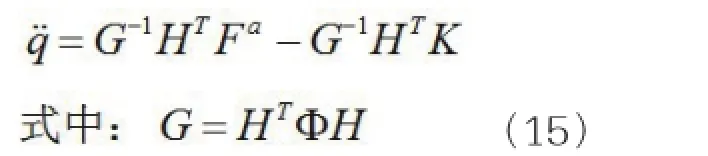
打磨机器人动力学仿真

本文第零至第二节已经介绍了打磨机器人的相关背景以及动力学建模的过程，本节介绍动力学仿真算例来分析末端执行器的运动轨迹。

如图3所示，打磨机器人是一个6R串联机器人。各连杆的几何参数和物理属性如表1和表2所示。本文算例分析中作用在各驱动关节上的扭矩为定值τ=[200000,1000,-8341.8,-65.1,-314.3,21.7]TNm。重力和作用在工具末端的工作阻力为作用在各连杆上的主动力。在此条件下，6R串联机械手的动力学响应可以用第二部分给出的动力学模型求解。仿真结果如图7-9所示。图7显示了一条轨迹。基坐标系下动态坐标点连接成一条曲线。红色三角和黑色圆圈分别表示起始点和终止点。我们期望机器人末端执行器走一条沿着Y轴方向的直线。然而末端执行器沿着X和Z方向也有位移。之所以这样，是因为驱动力给定和外部工作波动变化，或者主动力的和为一个正负波动的量。图8和图9分别显示基坐标系下的平动位移和局部坐标系下的转动角速度。

表1.机器人几何参数

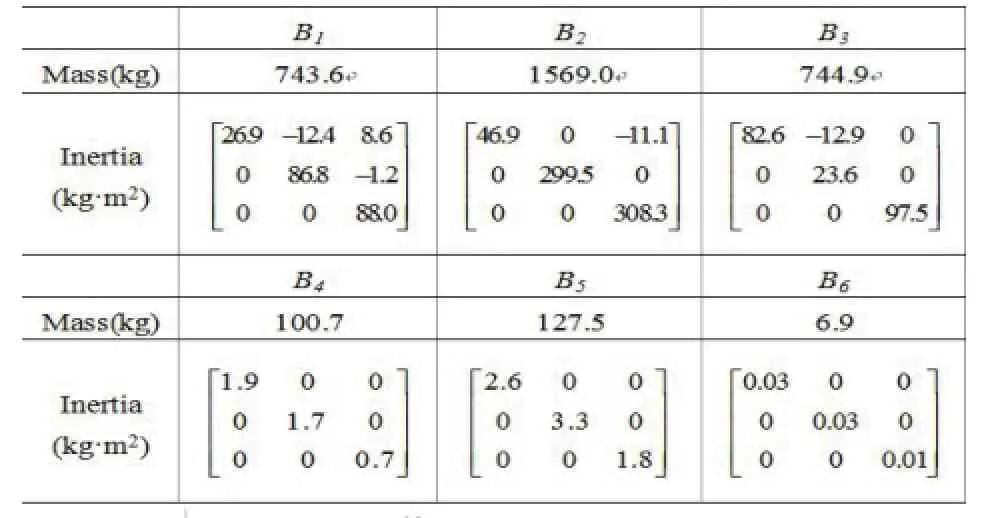
表2.机器人质量属性

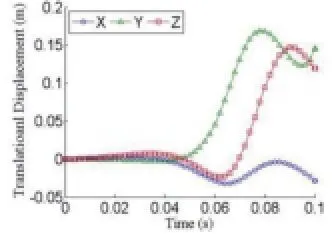
图8　末端执行器平动位移

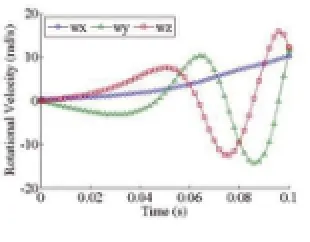
图9　末端执行器角位移

总结

本文采用Schiehlen方法建立了串联机械手系统动力学方程，对聚氨酯泡沫隔热层打磨机器人进行了动力学仿真分析。仿真结果表明打磨机器人末端执行器走了一条非预期的并且是大而波动的轨迹，这将不利于最终的打磨质量。因此，在隔热层打磨过程中控制工具的轨迹是有难度的。为了获得较好的打磨质量，需要考虑精确、快速的机器人主动控制算法。

（作者单位：上海航天设备制造总厂）

集团公司共性工艺研究项目（GXGY-2015-011），上海市军民结合专项