中央开槽箱梁风致静力稳定性研究

张凯歌

(中铁大桥科学研究院有限公司，湖北武汉，430034)

中央开槽箱梁风致静力稳定性研究

张凯歌

(中铁大桥科学研究院有限公司，湖北武汉，430034)

本文主要研究不同开槽率下的中央开槽箱梁在不同初始风攻角下的静风稳定性能。首先通过节段模型风洞测力试验得到±12°风攻角范围内六种开槽率下的箱梁断面的静风三分力系数，在此基础上运用三维非线性静风稳定分析方法对六种开槽率断面的桥梁结构进行静风稳定性分析。得出主要结论为：开槽箱梁静风失稳临界临界风速会随着开槽率的增加而提高，同时随着初始风攻角的减小而提高。

开槽箱梁；三分力系数；初始风攻角；开槽率；风致静力稳定性

概述

近年来由于桥梁的大跨化导致结构整体刚度弱化，从而对风的敏感性也大大增加，桥梁抗风问题成为大跨径桥梁设计的主要控制因素之一。桥梁的抗风问题主要包括风致振动和静风失稳，其中颤振和静风失稳可以导致桥梁结构的直接毁坏，在设计中应绝对避免。箱梁中央开槽作为一种提高颤振临界风速的有效方法[1][2][3]，被越来越多的运用到大跨度桥梁上，纵观全球范围内在建或者规划建设的跨境超过1500m的桥梁，主梁大都采用中央开槽箱梁。近年来的研究发现，跨度超过1500m的悬索桥静风失稳临界风速开始接近颤振发散临界风速，所以中央开槽箱梁静风稳定性能的研究极有现实意义。本文以我国跨度最大的西堠门大桥（主跨1650 m）为背景，首先通过风洞试验得到不同开槽率下的中央开槽箱梁的静风三分力系数，再运用三维非线性静风稳定分析方法对其静风稳定性能进行了研究，最后得出规律性的结论，对不同开槽率下的中央开槽箱梁的静风稳定性能进行评价。

风洞试验

试验模型

节段模型测力试验主要模拟气动外形的相似性，为了避免试验过程中模型自身变形和振动带来的误差，模型自身刚度应尽量大，本试验模型的竖弯与扭转振动频率均高于25Hz；为了考虑测力模型的端尾效应，模型长宽比在开槽率0%～80%范围内均大于 3，开槽率为 100%时受到试验设备和模型刚度的限制，长宽比取2.89，每个试验段上部均设置了补偿段。模型的具体参数如表3.1所示，断面参数如图3.1所示。

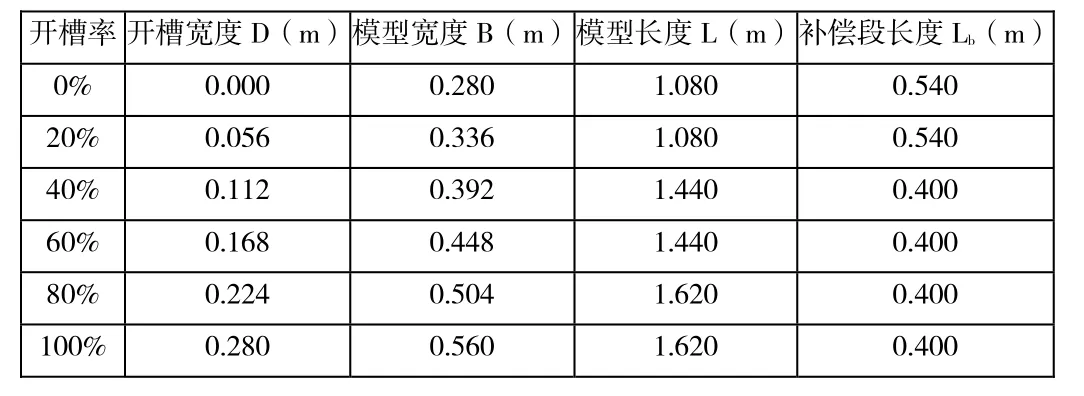
表 1测力模型设计参数

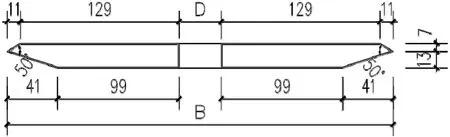
图 2 开槽箱梁测力模型断面参数（单位：mm）

表 2开槽箱梁测力试验工况一览表

试验工况

开槽箱梁节段模型测力试验中每种开槽率下有-12°～ +12°25个风攻角，共计 150个工况，具体见表 2。每组试验都从-12°开始，+12°结束，在加风速前和降风速后两次采零，试验风速为10m/s，每个风攻角下的测量都是在力信号完全稳定后进行。

静风三分力系数

各个开槽率下断面的静风三分力系数在体轴坐标系下随风攻角的变化如图 3所示：

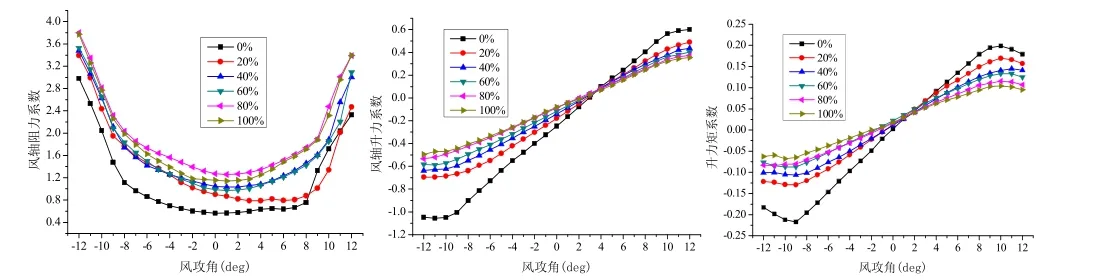
图 3各种开槽率下的静风三分力系数随风攻角的变化

三维静风稳定计算方法及其程序实现

大跨度桥梁三维非线性静风稳定分析方法是现阶段研究桥梁静风稳定性能的主流方法，主要考虑了三个方面的非线性：荷载非线性、几何非线性和材料非线性，其中荷载非线性和几何非线性对桥梁的失稳起到决定性作用，一般情况下，材料非线性虽然减小了结构的切线刚度，但是不会引起结构的失稳[4]，所以本文对开槽箱梁进行静风稳定性计算时只考虑了荷载非线性和几何非线性。

本文运用增量与迭代相结合的方法对结构的非线性平衡方程进行了求解，其中增量法实现对静风荷载的逐级增加，内层迭代进行结构的非线性计算，外层迭代寻找结构在给定风速下的平衡状态。现阶段判断结构失稳的方法大都采用观察结构失稳全过程的风速位移曲线，这种方法的优点是可以直观的判断结构的失稳，缺点是不能有效地寻找到具体的失稳风速。为了有效的寻找到结构失稳的临界风速，本文采用了文献[5]介绍的“优化的增量-迭代法”，通过引入外层迭代上限来控制风速增加步长，对风速增量计算进行了优化，通过控制风速增加步长的下限来控制内层迭代计算，进而提高计算效率。

本文通过运用APDL语言编写了计算程序，借助大型有限元计算软件ANSYS实现了对开槽箱梁静风稳定性的分析。编写程序的流程图如图 4所示：

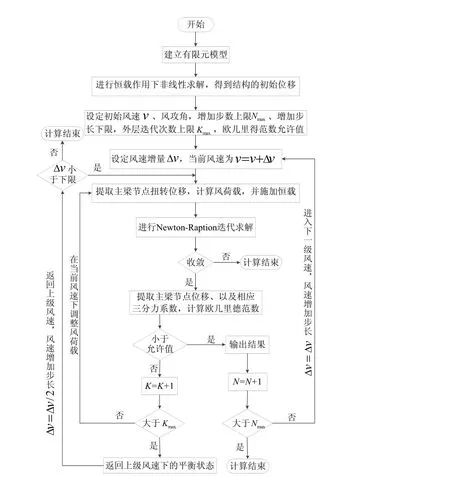
图 4三维非线性静风稳定计算程序流程图

计算模型

本文以西堠门大桥为结构背景，桥跨布置为578 m+1650 m+485 m=2713 m，如图 5所示。北跨和主跨采用连续钢箱梁，并由吊杆悬挂，南跨采用混凝土连续梁，不设吊杆，北塔墩处设置横向抗风支座，北锚和南塔墩处设置纵向活动、竖向约束支座，全桥为具有抗扭约束的纵向全漂浮体系。由于主梁为开槽箱梁，所以建模时采用双主梁模型，其中分体箱梁、箱型横梁和工字型横梁以及桥塔用空间梁单元BEAM 4模拟，主缆、吊杆用空间杆单元LINK 10模拟，部分恒载用MASS 21单元模拟，为了方便风荷载的施加和主梁位移的提取，在主梁形心处设置了一道虚拟主梁，计算模型如图 6所示。

图 5西堠门大桥桥跨布置图

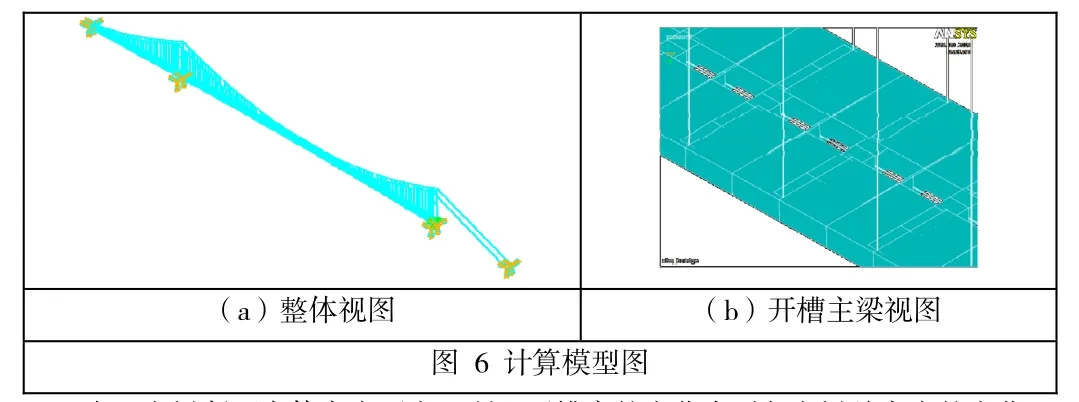
（a）整体视图 （b）开槽主梁视图图 6 计算模型图

表 3开槽箱梁静风稳定计算工况表

由于主梁断面实体宽度不变，所以开槽率的变化会引起主梁总宽度的变化，进而会使主梁断面刚度以及所处结构的刚度有相应改变，会影响到开槽箱梁的静风稳定性能。本文在开槽率变化时主梁刚度和所处结构刚度做出相应调整，并考虑开槽宽度变化引起的静风荷载变化，此计算模型模拟了结构的真实受力状态，可以对不同开槽箱梁的静风稳定性能做出准确评价。

计算模型的计算工况包括六种主梁形式，每种主梁形式又包括-3°、0°和3 °三个初始风攻角，共18个计算工况，如表 3所示。

风攻角 -3°、0°、+3°

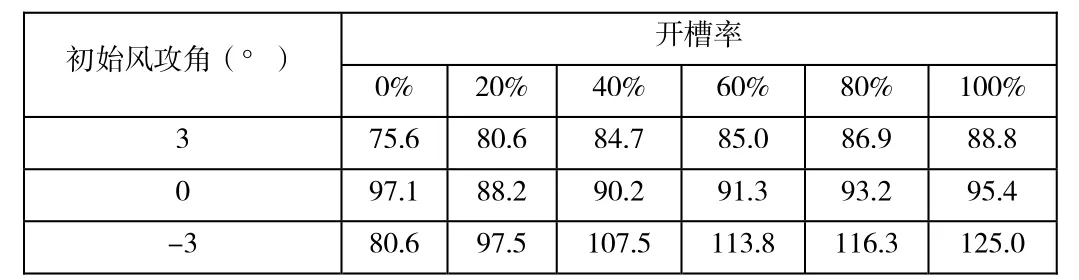
表 4不同开槽率箱梁在不同初始风攻角下的静风失稳临界风速（m/s）

计算结果

考察开槽箱梁的静风稳定性能关键参数就是最终失稳的临界风速。当断面开槽率变化时，各种工况静风失稳的临界风速计算结果汇总如表 4所示，静风失稳临界风速随开槽率变化曲线如图 7所示。

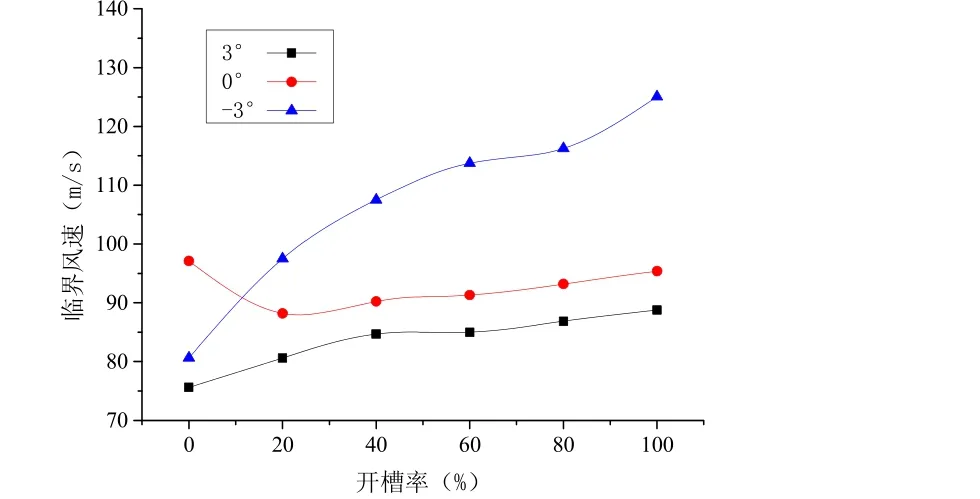
图 7静风失稳临界风速随开槽率变化曲线

观察图 7，并结合表 4可以得出：

1.开槽箱梁静风失稳临界风速随开槽率的变化有着明显的规律性：

（1）在初始风攻角为±3°时，断面的静风失稳临界风速随开槽率变化有着相同的规律，即随着断面开槽率的增加静风失稳临界风速增高。

（2）在0°初始风攻角下，零开槽断面的静风失稳临界风速最高，开槽后断面的静风失稳临界风速会降低，但是会随着开槽率的增加而增高。

2. 初始风攻角对开槽箱梁的静风失稳临界风速有一定影响：断面的静风失稳临界风速会随着初始风攻角减小而增高。

结论

通过对-3°、0°和+3°初始风攻角下六种开槽率箱梁模型的风致静力稳定性分析，得出以下主要结论：

1. 中央开槽箱梁风致静力稳定性随开槽率的变化有着明显的规律性，静风失稳临界风速随开槽率的增加大致呈现出增高的趋势。

2. 初始风攻角对每种开槽率箱梁的静风稳定性能有着相同的影响，断面的静风失稳临界风速会随着初始风攻角的减小而增高。

3. 中央开槽箱梁在风荷载作用下位移随风速变化呈现出很强的非线性特征，并且失稳时呈现出很强的弯扭耦合特征说明大跨度悬索桥结构的风致静力稳定性问题属于第二类稳定，对其进行风致静力稳定性分析时要充分考虑非线性因素。

[1]SATOH, OGIHARAK. Aerodynamic Characteristics of Slotted Box Girders [C]//The Hong Kong Institution of Engineers. Proceedings of Bridges into 21st Century. Hong Kong: The Hong Kong Institution of Engineers,1995:721-728.

[2]杨詠昕.大跨度桥梁二维颤振机理及其应用研究:[博士学位论文].上海:同济大学,2002.

[3]曹丰产.桥梁断面中间开槽对颤振稳定性的影响[J].同济大学学报:自然科学版,2002,30(5) :551-556.

[4]程进，江见鲸，肖汝诚，等.考虑几何与材料及静风荷载的非线性因素的大跨径桥梁静风稳定分析方法[J].应用力学学报，2002，19(04) ：117-121.

[5]张文明. 多主跨悬索桥抗风性能及风致灾变全过程研究:[博士学位论文].上海:同济大学,2011.

G322

B

1007-6344（2016）03-0341-02

?

张凯歌,(1987-),男,助理工程师,2013年毕业于同济大学建筑与土木工程专业（E-mail：10kaige_zhang@tongji.edu.cn）.