一种测量金属薄板拉伸应变硬化指数的方法

田晨超，许 飞，焦 磊，张 娟

(西北有色金属研究院，西安 710016)

一种测量金属薄板拉伸应变硬化指数的方法

田晨超，许 飞，焦 磊，张 娟

(西北有色金属研究院，西安 710016)

为实现视频引伸计在应变硬化指数n值测试过程中的应用，以弥补短行程接触式引伸计测量范围的不足，依据GB/T 5028—2008中有关薄板拉伸应变硬化指数的测试方法，采用INSTRON 5985视频引伸计，通过软件Bluehill 3的自动测量及人工测量方式在规定回归区间进行了n5～15值的测定，并采用简化公式进行了验证。结果表明，n5～15值均为0.18，满足能力比对试验结果的测试要求。

应变硬化指数；视频引伸计；自动测量；人工测量

基于经验，Hollomon于1944年建立了塑性拉伸变形的指数方程，同时将应变硬化指数n引入塑性力学，至此，对于金属材料的塑性变形研究便从单一的唯象观测推进到理论分析阶段[1-2]。金属材料的应变硬化性能集中反映了屈服后的塑性变形和强化行为。作为材料的安全性能指标，应变硬化指数与断裂韧性之间存有相关性，依此可建立相应的断裂判据[3]。应变硬化指数在工程上也已得到广泛应用[4-5]，对于金属容器、车辆蒙皮及管材扩口加工等冷塑成型加工工艺而言，获取材料的应变硬化指数，可预知其在成型过程中的均匀变形程度及抵抗偶然过载的能力，避免由于局部变形集中而造成材料的报废。

目前，用于计算应变硬化指数n值的方法主要有差分平均法、两点法、解析拟合法及线性回归法，针对材料的不同屈服特性理应选取合适的计算方法[4,6]。非接触式视频引伸计作为材料受力下应变分量的一种采集手段，近些年已广泛应用于单轴拉伸试验过程中相关力学性能指标的测定[7-8]。笔者依据GB/T 5028—2008中有关拉伸应变硬化指数的测试内容[9]，采用INSTRON 5985视频引伸计及附带软件Bluehill 3进行了n5～15值的自动测量，并在均匀塑性变形阶段选取以几何级数分布的7点应力-应变值进行了n5～15值的人工测量，对其测试结果进行了比对分析。实现了视频引伸计在测量应变硬化指数上的应用，弥补了短行程接触式引伸计的不足。

1 试验材料及设备

试验材料采用上海宝钢股份公司提供的冷轧钢板能力比对试样，板厚0.8mm，工作区25mm×100mm(长度×宽度)，原始标距50mm。

试验设备采用美国INSTRON 5985系电子万能材料试验机，最大载荷250kN，载荷精度0.5级，符合GB/T 16825.1—2008静力单轴试验机的精度要求[10]。配套的非接触式视频引伸计量程0～200mm，分辨率优于0.000 5mm，满足测试要求。

2 试验方法

采用千分尺及游标卡尺对板状试样工作区的厚度及宽度分别进行实际测量，操作过程及原始横截面积的测定均符合GB/T 228.1—2010金属材料室温拉伸试验标准的相关要求[11]。原始标距的标记采用手工划线机，标记之后，人工测量50mm标距长度，准确度符合±1％。同时，在板状试样表面工作区的中心以50mm标距为起始点做好标记，以便视频引伸计跟踪测量标距的实时伸长量。

相关研究表明，不同的加载控制模式及加载速率均对应变硬化指数n值产生影响，通常随加载速率的增加n值呈增大趋势[1,12]。本次试验速率依据能力比对的测试要求，加载路径采用衡量位移控制模式，即屈服前采用3mm/min，屈服后30mm/min的试验速率，采用人工速率切换。对于呈现明显屈服平台的材料应在形变强化开始阶段及稍小于测定应变硬化指数的回归区间的下限开始切换速率。若材料呈单调上升的均匀变形行为(即无上、下屈服)时，速率切换点应在过非比例延伸强度(通常取RP0.2)及稍小于规定回归区间的下限区域。标准要求，计算应变硬化指数的回归区间应处于材料的均匀塑性变形区，且上限应稍小于最大力所对应的塑性应变，该过程试验速率应保持不变，平行长度部分的应变速率不得高于0.008s-1，直至试样断裂[9]。

3 试验结果及分析

试验结束后，分别采用软件Bluehill 3的自动测量及人工测量方式计算了薄板试样的拉伸应变硬化指数n值。薄板的应力-应变曲线如图1所示。由图1可见，其屈服特性具有明显的上下屈服的物理特性。薄板常规的力学性能见表1。

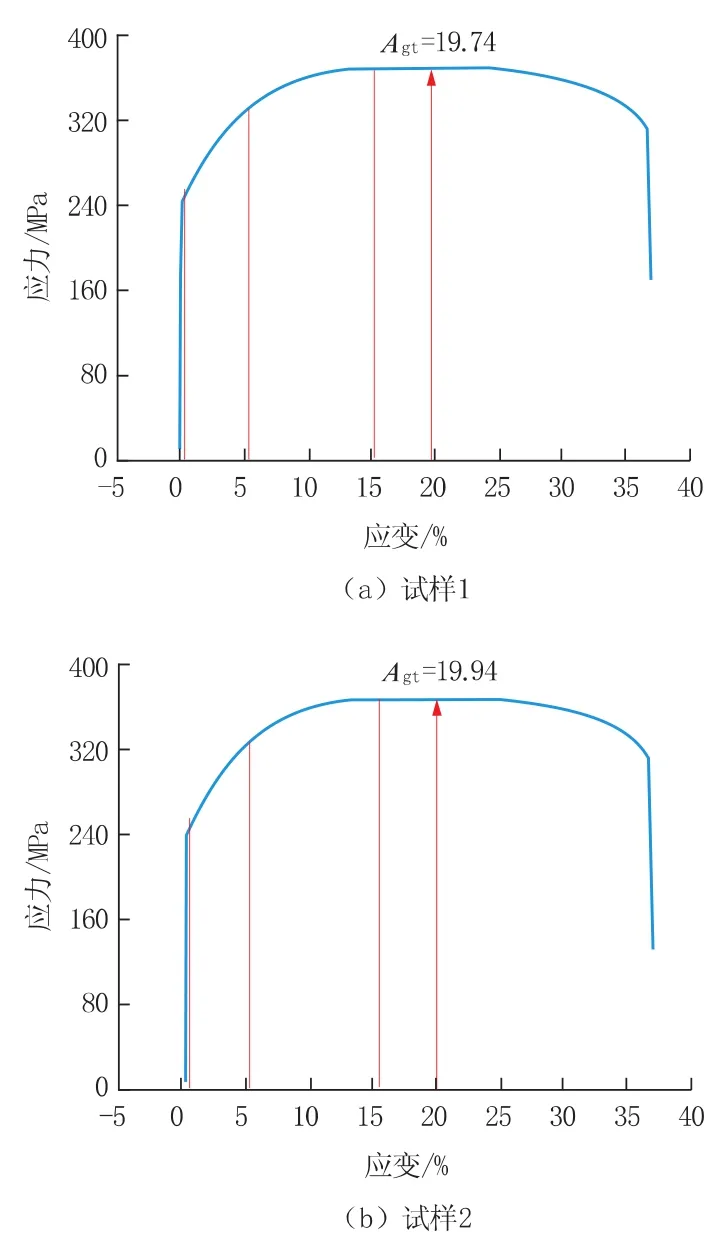
图1 薄板的应力-应变曲线

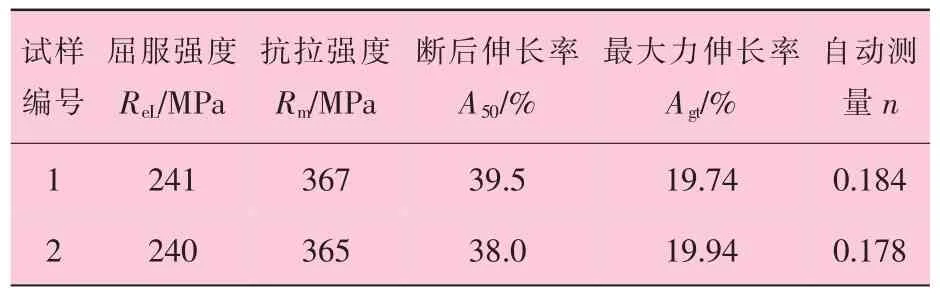
表1 薄板常规的力学性能

有关研究发现[4]，均匀塑性变形阶段线性回归区间范围的选取对应变硬化指数n值的计算结果同样产生影响，不存在明显的规律。此次基于能力比对试验的要求，软件自动测量n值的线性回归区间的塑性应变范围规定为5％～15％。软件所测得的两组试样n值见表1，其代数平均值为0.18，相对偏差为-3.3％(以1#试样为准)，离散性较小。

依据GB/T 5028—2008，采用人工测量方式对n值的计算结果进行了比对。在应力-应变曲线的均匀塑性变形阶段(应变范围5％～15％)选取以几何级数分布的7点工程应力-应变值(R-A)进行了n5～15值的计算，结果见表2。基于Hollomon提出的真实应力-应变关系式，即

式中：S—真应力；

e—真应变；

n—应变硬化指数；

K—强度系数。

关系式(1)的对数方程为

基于工程应力-应变(R-A)与真实应力-应变间的关系，S＝(1+A)R，e＝ln(1+A)，对公式(2)可采用最小二乘法计算拉伸应变硬化指数n值，即

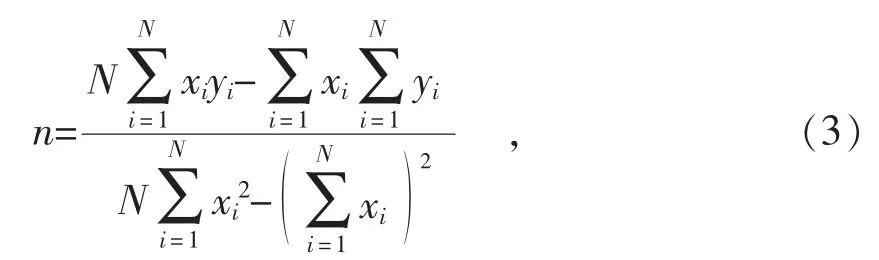
式中，N为选取的7点应力-应变值，x＝lne，y＝lnS。

表2 人工计算n值

通过人工计算得知，两组薄板试样n值的代数平均值为0.18，相对偏差为-2.2％，数值修约后与自动测量n值的结果等同，且数据的离散性更小。反馈的试验结果表明，所测得的n值均在能力验证指标要求的范围内，结果良好。实现了视频引伸计在薄板试样拉伸过程中应变的实时测量，为准确计算n值提供了应变的采集途径，弥补了短行程接触式引伸计测量范围的不足。

由于n值的计算过程较为复杂，为满足工业生产的需要，有关n值简化计算方面的工作也已展开[13-14]。 方健等[14]人的研究结果表明，当n值较小时，采用国际回归法计算的规定应变范围内的n值与简化公式所得n值的相对偏差在5％以内。

均匀塑性变形阶段的应变沿试样平行段均匀分布，其变形程度可用最大力伸长率Agt表示，与n值均可作为衡量材料成型性能的重要指标。基于Hollomon关系式全微分得出的n值计算的解析拟合法，存在关系式

根据塑性体积不变原理及工程应力-应变曲线载荷极值位下dR/dA＝0的边界条件，理论推测出均匀变形右侧边界处应变硬化指数n值满足

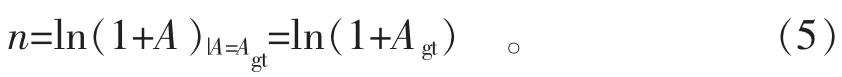
基于视频引伸计对应变的实时测量，通过工程应力-应变曲线可直接得出Agt值。将两组试样的Agt代入式(5)，计算得出载荷极值位下的n值见表3。

表3 载荷极值位下的n值

由简化公式计算所得的应变硬化指数n值可看出，其均值为0.18，相对偏差为1.1％，相比自动测量和人工测量方式，所得数据满足n值的测试要求，且离散性更小。结果表明，拉伸应变硬化指数n值与最大力伸长率Agt存在相关性。同时，对于n值不高的材料，基于工程应力-应变曲线，该式可用于n值的简化估算，并可对标准规定的n值的计算结果进行验证，为理论推导出的相关n值计算的简化公式的合理有效应用提供了试验佐证。

4 结 论

(1)Bluehill 3软件的自动测量及人工测量方式下规定回归区间的拉伸应变硬化指数n5～15值均为0.18，满足能力比对试验结果的测试要求。

(2)实现了视频引伸计在n值测试过程中的应用，弥补了短行程接触式引伸计测量范围的不足。

(3)简化公式所得n值为0.18，为应变硬化指数的准确测得提供了有效验证，并为相关n值的合理有效简化计算提供了试验佐证。

[1]宋玉泉，管志平，马品奎，等.拉伸变形应变硬化指数的理论和实验规范[J].金属学报，2006，42(7)：673-680.

[2]束德林.工程材料力学性能[M].北京：机械工业出版社，2007.

[3]郑美彬.形变强化的测试及其工程应用[J].福州大学学报，1989，17(2)：64-69.

[4]苏洪英，隋晓红，李文斌，等.拉伸应变硬化指数的测试及方法比较[J].理化检验-物理分册，2011(11)：682-685.

[5]冯建友.AZ31镁合金板单向拉伸应变硬化指数的试验测定[J].机械工程与自动化，2014(2)：99-100.

[6]常东华，周晓，魏佰友，等.应变硬化指数n值的测定和应用[J].理化检验-物理分册，2006，42(5)：242-244.

[7]彭真.接触与非接触式引伸计自动测定冷轧薄板断后伸长率的结果比较[J].金属材料与冶金工程，2010，38(5)：30-32.

[8]胡世军，张红香，张代录，等.非接触式视频引伸计在力学性能试验中的应用[J].科技导报，2012，30(19)：60-62.

[9]GB/T 5028—2008，金属材料 薄板和薄带拉伸应变硬化指数(n值)的测定[S].

[10]GB/T 16825.1—2008，静力单轴试验机的检验 第1部分：拉力和(或)压力试验机测力系统的检验与校准[S].

[11]GB/T 228.1—2010，金属材料 拉伸试验 第1部分：室温试验方法[S].

[12]谭洪峰，王萍，杨雷，等.应变硬化指数n值与拉伸控制模式及拉伸速率关系的探讨[J].物理测试，2010，28(6)：13-16.

[13]VILLAMANAN J E，APARICIO M L.计算应变硬化指数的简易方法[J].金属材料研究，1990，16(1)：51-54.

[14]方健，魏毅静，王承忠.拉伸应变硬化指数的解析测定及力学分析[J].塑性工程学报，2003，10(3)：12-17.

One Method of Measuring Metal Sheet Tensile Strain Hardening Exponent

TIAN Chenchao,XU Fei,JIAO Lei,ZHANG Juan
(Northwest Institute of Nonferrous Metal Research,Xi’an 710016,China)

In order to realize application of the video extensometer in the strain hardening exponent n value testing process,to make up for the measurement range shortage of the short stroke contact extensometer.Based on the related test methodof metal sheet tensile strain hardening exponent in GB/T 5028—2008,using INSTRON 5985 video extensometer to measure n5～15value,by means of the software Bluehill 3 automatic measurement and manual measurement methods in the specified regression interval,and the simplified formula was used to verify the methods.The results showed that the n5～15value is 0.18,which meets the requirements of the ability comparison test results.

strain hardening exponent;video extensometer;automatic measurement;manual measurement

TG113.2

B

10.19291/j.cnki.1001-3938.2016.09.013

田晨超(1986—)，男，陕西富平人，工程师，硕士，主要从事金属材料的检测分析工作。

2016-07-12

罗 刚