构造几何图形,巧解数学问题
2016-12-17江苏省射阳县第六中学224300
江苏省射阳县第六中学(224300)
陈广州●
构造几何图形,巧解数学问题
江苏省射阳县第六中学(224300)
陈广州●
数学问题的解决有赖于数学方法的运用,一个好的数学方法可以帮助我们更快更顺利的解决问题.我们常见的数学方法有代数、算术等.图形可以直观地展示问题,因此,通过几何图形来解题,是不错的切入点,在很大程度上可以简化解题步骤.基于此,我将通过实例,探讨如何使用图形解决数学问题.
一、巧解角的度数问题
例1 在同一平面内,若∠AOB=70°,∠BOC=15°,求∠AOC的度数.
解析 下面是一位同学的解题过程,我们来看看是否正确.∠AOC=∠AOB-∠BOC=70°-15°=55°,则∠AOC=55°.答案正确,但用上述方法解题时造成了丢解的情形,此时图形法的优势显现了出来.
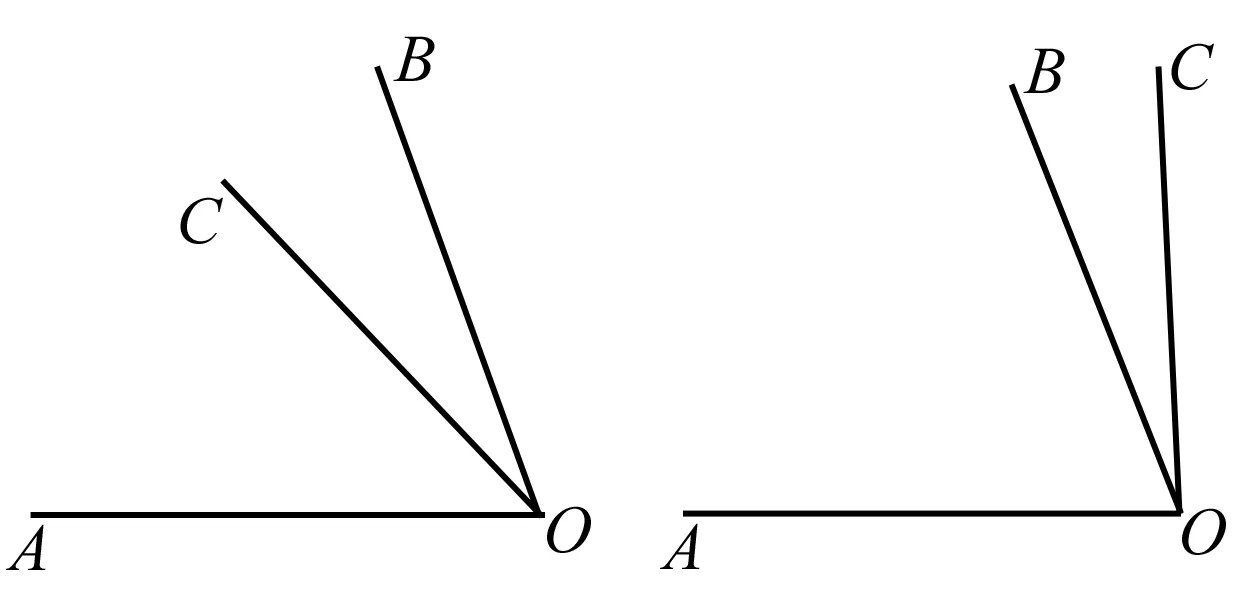
我们可以画出各个角的相对位置,那么在画图的时候我们会发现,会有两种情况,如图所示,第二种情况就是∠AOC=∠AOB+∠BOC=70°+15°=85°,则∠AOC=85°.
对于忽略第二种答案的思维定势,通过图形的构造打开了思维,得到问题的最终答案.图形法在解题的同时提供给学生一个新的思考方式,可以激发学生的探索兴趣.
二、巧证不等式问题
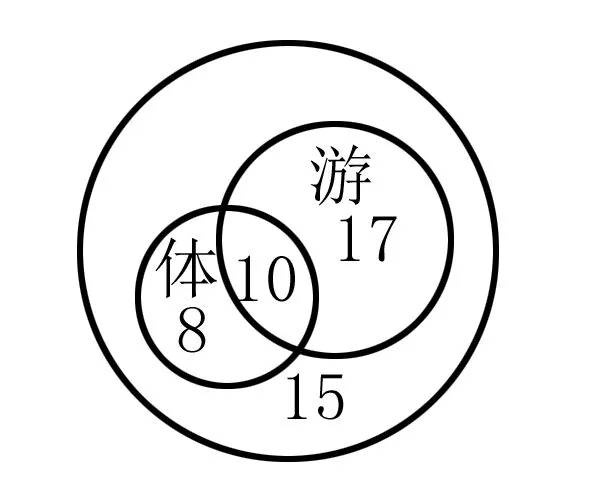
例2 已知六个正数A、B、C、a、b、c满足A+a=B+b=C+c=K,求证:aB+bC+cA 解析 如果只用代数或者算术知识很难解出此问题,但是我们可以根据题中的条件构造出一个边长为K的正三角形,然后再根据三角形的面积等关系解决此问题.设△DEF是一个边长为K的等边三角形,GHI各顶点分别为DE,EF,FD上的点,且DG=A,GE=a,EH=B,HF=b,FI=C,ID=c,如图所示. 题中所给的等式条件与等边三角形的三边正好符合,三角形的图形构建就随之而来,再运用面积关系求解,这种构造图形的思路正是解此类题目的精髓所在. 例3 五人进行羽毛球单打比赛,已知A比赛4场,B比赛3场,C比赛2场,D比赛1场,那么E比赛几场? 解析 此题凭借列式求解会相当繁琐,但只要我们换个角度,将文字描述转化为二维图形,便可轻松求解. 如图所示只要我们画出这个图形,以平面内任意三点之间的连线来表示一场比赛,那么此图就是我们所求问题的解. 此题中构造图形方法的神奇之处在于并没有列式计算就得出了答案,在化繁为简的同时开拓学生的思维,提高解题效率. 例4 某班有50个人,会体操的有18人,会游泳的有27人,游泳体操都不会的有15人,那么即会体操又会游泳的有多少人. 解析 这是数学问题在实际生活中的应用,并不是所有的数学问题都需要代数运算,正如本文介绍的那样,巧妙的构造图形可以让计算更简便,思路更清晰. 画出三个圆圈,分别代表本班的全部人数,会游泳的人数和会体操的人数.这也是韦恩图的正确使用方法.游泳体操都不会的有15人,那么至少会一项运动的有35人,则由图可知两项都会的有27+18-35=10人. 本题本身没有几何图形,但是我们可以通过观察,从数形结合的角度出发,构造出一个图形,使题中已知的数量关系在图形上得到完美体现,用图形关系解题. 有些数学问题并不是非要用代数方法来解决的,通过转换思路,改变思维,在平面几何的领域构造出图形,在锻炼学生的创造力与想象力的同时加深对数量关系的理解,简化运算过程,让难以解决的问题峰回路转. G632 B 1008-0333(2016)23-0009-01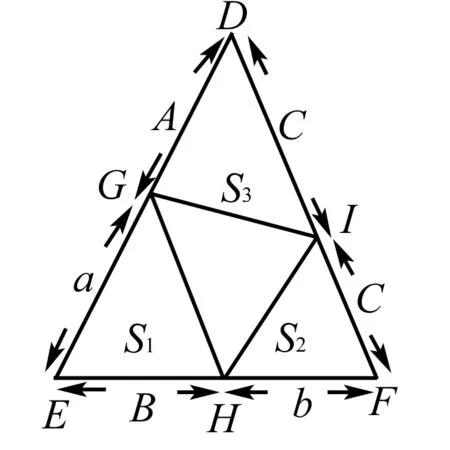
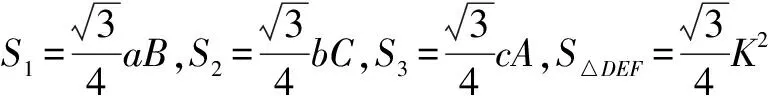

三、巧解比赛问题

四、巧解人数问题