代数搭桥，巧算面积

安徽省芜湖市镜湖区教育局(241000)

吴定根●



代数搭桥，巧算面积

安徽省芜湖市镜湖区教育局(241000)

吴定根●

马克思说过:“代数是懒人的算术”.一语道破了代数解题的便捷性.学会用代数法解题，就好比掌握了解题的“金钥匙”.

一些数量关系较为隐蔽的几何图形的面积计算，仅机械地应用几个求积公式，是难以解答的.如果能运用代数思想，抓住问题与条件间的纽带，充分利用已知条件中的数值，让代数牵线搭桥，就可巧算面积.下面就是几个很好的实例.

例1 已知图中四分之一圆的面积为157cm2，求阴影部分的面积.

怎样计算正方形面积，是解答本题的关键.可以1/4圆的面积157cm2为突破口，追本求源.借助代数，将1/4圆的半径(正方形边长)设为rcm，其面积可表示为：πr2/4，先求出r2值. 因为πr2/4 = 157, 所以r2=157÷(1/4)÷3.14=200(cm2)，而r2的值所表示的意义，不正是正方形面积吗？这样，问题就迎刃而解了，阴影部分的面积是： 200-157=43(cm2).

例2 已知右图中的两个正方形相差400 cm2.求圆A比圆B的面积多多少平方厘米.

乍看此题，好像这两幅图没有直接关系.其实，题中的两个正方形的面积差，已将本无直接关系的两图紧系在一起了.

从两个正方形的关系入手，创设新的条件后，再解决两圆面积差的问题.

令大正方形边长为A圆的两个半径(2R)，那大正方形的面积可表示为： 2R×2R=4R2. 再设小正方形边长为B圆的两个半径(2r),那么小正方形面积可表示为： 2r×2r=4r2.由两个正方形的面积差400cm2可知：4R2-4r2=4(R2-r2)=400， 那么，R2-r2=400÷4=100(cm2) .

这个条件的创设，为求两个圆面积差铺平了道路： 3.14×R2-3.14×r2=3.14×(R2-r2)=3.14×100=314(cm2)

例3 如图，任意五边形ABCDE的周长为64cm，O点到各边的距离都是12cm，求五边形ABCDE的面积.

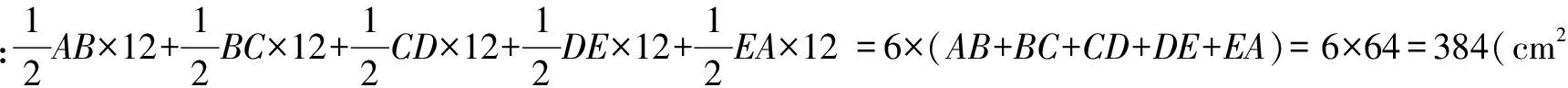
例4 求右图的面积.

例5 右图长方形面积为35cm2，左边直角三角形的面积为5cm2，右上角直角三角形面积为7cm2,求阴影部分的面积.

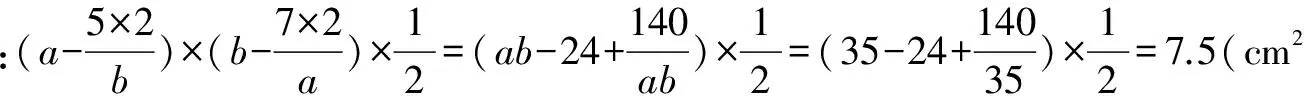
因此，图中的阴影面积为：35-(7+5+7.5)=15.5(cm2)

以上各题都是抓住题中隐蔽条件的连接点，依据已知条件的数值，用代数法求出相关未知量的数值，以转化条件，达到化难为易之目的，巧算面积.这里，代数仅起到桥梁作用，而并不需要求代数的解.可见，学会从代数的视角思考算术求积问题，让代数与算术完美结合，确实是将复杂问题简单化的有效策略.当然，上述各题也可以用其他方法解答.本文只是以此为例，谈如何运用代数法求积而已.

G632

B

1008-0333(2016)23-0007-01