基于Copula函数的开都河年径流预测

魏光辉

(新疆塔里木河流域管理局， 新疆 库尔勒 841000)



基于Copula函数的开都河年径流预测

魏光辉

(新疆塔里木河流域管理局， 新疆 库尔勒 841000)

河川径流量的准确预测对于水库调度、区域水资源优化配置具有重要意义。本文以新疆开都河为例，运用Copula函数将自变量和因变量的相关程度和相关模式有机结合，构建两变量联合分布函数，研究两变量与联合分布之间的相依结构；在此基础上，根据样本值未知的因变量边缘分布与联合分布关系，结合样本值己知的自变量概率分布，对因变量未知值进行预测。结果表明：基于Copula函数的预测方法原理明晰、计算简便、性能稳定、预测精度较高。

年径流； 预测； Copula函数； 联合分布； 开都河

Copula函数是一类将两个或多个随机变量的任意边缘分布函数进行连接得到两变量或多变量联合分布函数的连接函数，该函数克服了多变量联合分布难以确定的困难，能够简洁合理地构造联合分布函数，清晰灵活地刻画变量间的相关性关系，使变量的边缘分布和相关性结构分别得到研究，不产生信息失真。

目前，Copula函数广泛应用于变量频率分析计算。在水文水资源领域，Copula函数在洪水频率分析[1]、干旱特征分析[2]及水文随机模拟[3]等方面均取得了很好的应用成果，但在预测问题上的应用相对较少。目前常见的水文预测模型有神经网络[4]、组合模型[5]、分布式模型[6]等，本文将Copula函数应用于预测研究，提出Copula预测方法。通过Copula函数构建自变量和因变量的联合分布函数，分析自变量和因变量的相关程度和相关模式；在此基础上，结合样本值已知的自变量概率分布特点，细致研究样本值未知的因变量概率分布与联合分布的关系，对因变量未知值进行预测。对新疆开都河年径流预测的结果表明：该方法原理明晰、计算简便、预测精度较高。

1 Copula方法介绍

1.1 Copula函数

二元Copula函数C(·,·)，是定义域为[0,1]2，有零基面且二维递增,对任意变量u、v∈[0,1]满足C(u,1)=u和C(1,v)=v的函数。即C(·,·)是一个边缘分布服从[0,1]均匀分布的二元分布函数，且对于定义域内任意一点(u,v)均有0≤C(u,v)≤l。根据Sklar定理[7]，令H(·,·)为具有边缘分布F(·)和G(·)的联合分布函数，则存在一个Copula函数C(·,·)，满足

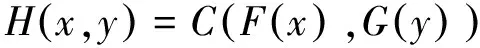
(1)

若F(·)和G(·)连续，则C(·,·)唯一确定；反之，若F(·)和G(·)为一元分布函数，C(·,·)为相应的Copula函数，则由式(1)定义的函数H(·,·)是具有边缘分布F(·)和G(·)的联合分布函数。

同时，二元Copula函数的密度函数c(·,·)与联合分布函数H(·,·)的密度函数h(·,·)满足

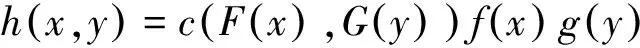
(2)

由此可见，Copula函数的Sklar定理为求取联合分布函数及其密度函数、分析变量之间相关结构提供了一条便捷的新途径。

Copula函数C(·,·)的具体形式多样，其中阿基米德Copula函数是最为常用的一类，即

(3)

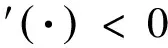
φ-1(·)——生成元φ(·)的逆函数，在[0，∞)区间完全单调。

阿基米德Copula函数由其生成元唯一确定，其分布函数和密度函数分别为

(4)

(5)

式中u、v——意义同前；

θ=2τ/(1-τ)。

τ为Kendall秩相关系数：

(6)

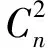
xi、xj、yi、yj——样本取值，当(xi-xj)(yi-yj)>0时sign=1，当(xi-xj)(yi-yj)<0时sign=-1，当(xi-xj)(yi-yj)=0时sign=0。

检验Copula函数是否能够正确刻画变量的联合分布，可以通过经验相关函数和Copula函数的曲线拟合情况进行判断[8]。经验相关函数Cemp(·,·)是直观反映样本空间分布特点的函数，表达式为

(7)

一般采用离差平方和准则(OLS)对拟合情况进行量化评价，OLS值越小拟合越好：

(8)

式中Cemp,i、Cc1,i——在曲线拟合图中经验相关函数和Copula函数的对应取值。

1.2 Copula预测方法基本思路

假定随机变量X为自变量，随机变量Y为因变量，Copula预测方法的基本思路如下：首先，运用Copula函数对随机变量X和Y的边缘分布函数进行连接，构建随机变量X和Y的联合分布函数；其次，在己知t+1时变量X的实测值或估计值xt+1条件下，基于Copula函数建立变量Y的边缘分布和联合分布的联系，结合相关分析建立变量Y的边缘分布与联合分布的关系表达式；最后，根据关系式对变量Y的t+1时值yi+1进行预测。

1.3 Copula预测方法的步骤

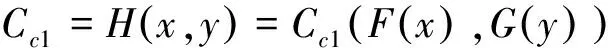
c.已知变量X在t+1时的样本值xt+1，则相应的边缘分布概率为F(xt+1)，将F(xt+1)代入式(4)，可得

(9)

d.将a和b中计算得到的数对进行多项式拟合，得到Cc1和v的近似关系式：

(10)

式中a1、a2、…、am+1——多项式系数，m取值视拟合情况而定。

式(10)从另一角度表示Y的边缘分布与X和Y的联合分布之间的联系。

e.联立式(9)和式(10)，求解得到v*，则变量Y在t+1时的预测值为

(11)

式中G-1(·)——边缘分布函数G(·)的逆函数。

2 模型应用

开都河位于新疆焉耆盆地内，河流发源于天山中部的依连哈比尔尕山南坡，多年平均径流量为35.18亿m3。河流出山口处至下游分别设有大山口水文站与焉耆水文站。本文根据大山口水文站(出山口处)与焉耆水文站(下游)1956—2012年的年径流资料(见图1、图2)，令大山口水文站年径流为自变量X、焉耆水文站年径流为因变量Y，以预测2006—2012年焉耆水文站年径流yt+1为例介绍模型的应用。选取1956—2005年径流资料为建模样本(n=50)，2006—2012年径流资料为预测样本(n=7)。

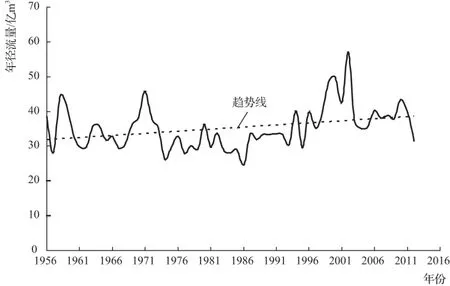
图1 大山口水文站年径流变化曲线

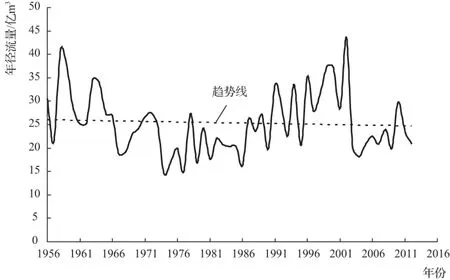
图2 焉耆水文站年径流变化曲线

采用P-Ⅲ型分布描述变量X与Y的概率分布[9-10]，由矩法估计得到变量X的均值、变差系数Cv及偏态系数Cs分别为35.27亿m3、0.178与0.373；同理，得到变量Y的均值、变差系数Cv及偏态系数Cs分别为25.37亿m3、0.265与0.615。根据Clayton Copula函数构造变量X和Y的联合分布函数H(x,y)=Ccl(F(x),G(y))，其中Kendall秩τ=0.757、参数θ=14.122。

通过对Clayton Copula函数与经验相关函数拟合，得到模型OLS值为0.045，可见计算分布与经验点据拟合较好，说明基于Copula函数构建联合分布的方法是可行和可靠的。

已知2006年开都河大山口水文站年径流量xt+1为40.3亿m3，其分布概率F(xt+1)=0.823，带入式(9)可得：

(12)

根据式(10)，将数对进行线性拟合，得

Cc1=0.813v-0.012

(13)

联立求解式(12)和式(13)，得v*=0.833。由式(11)和P-Ⅲ型分布G(y)的逆函数得

(14)

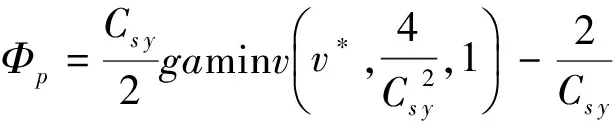
由式(14)最终得到焉耆水文站2006年的年径流预测值。同理以1956—2006年径流资料为建模样本对2007年焉耆水文站年径流进行预测。依此类推，逐一预测焉耆水文站2008—2012年的年径流，结果见下表。

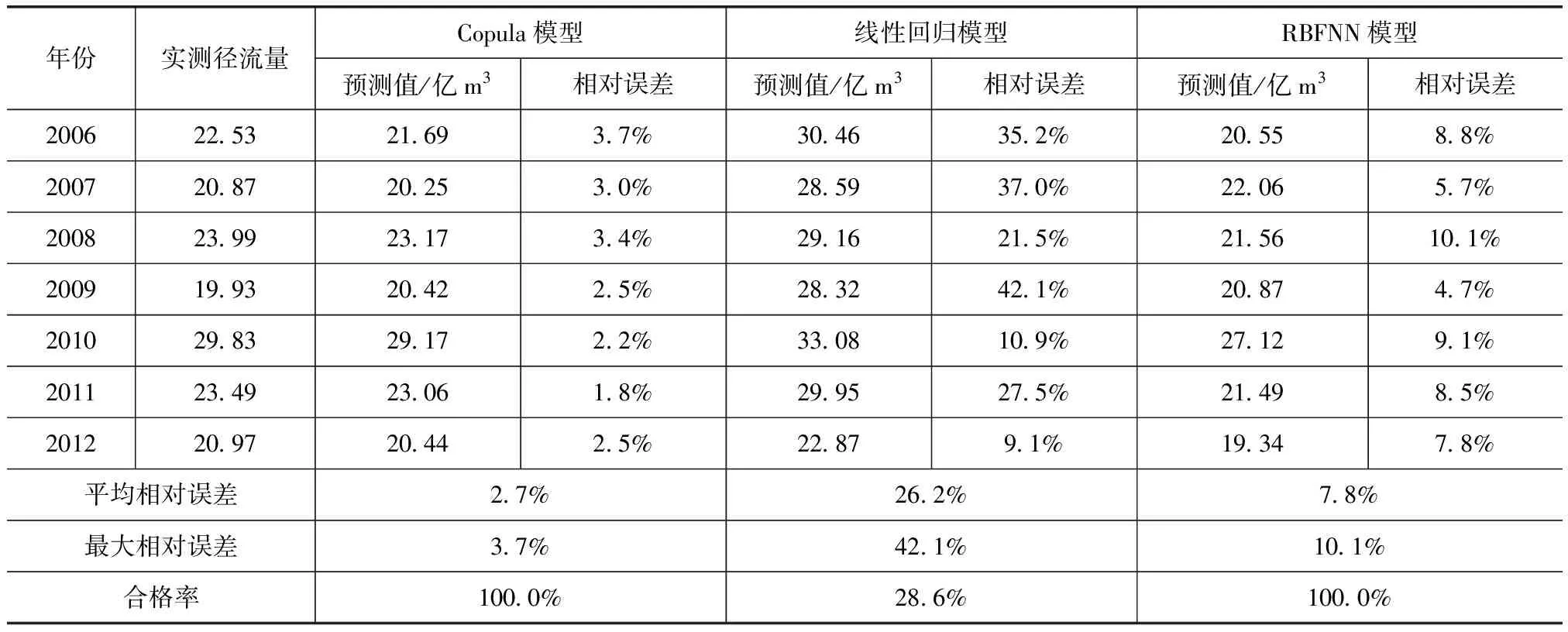
年径流预测结果表

为对比分析，分别采用线性回归模型、径向基函数神经网络(RBFNN)模型预测焉耆水文站2006—2012年径流量。

线性回归模型是通过建立回归方程式Y=a+bX，由X预测Y。根据1956—2005年开都河大山口水文站和焉耆水文站的年径流资料可求得a=-4.4378，b=0.8652，据此由大山口水文站2006—2012年径流量可计算得焉耆水文站同期年径流量，成果见上表。

RBFNN是以高斯函数为隐层节点激励函数的一种三层前馈人工神经网络[11]。大山口水文站、焉耆水文站的年径流分别为变量X和Y，以两变量1956—2005年径流系列为学习样本，对模型进行训练，由最近邻聚类学习算法完成迭代，确定高斯函数的均方差、隐层节点数以及各隐层节点到输出节点的权重。在此基础上，输入X变量(2006—2012年的径流量)，对Y变量同期值进行预测，成果见上表。

计算各模型的平均相对误差和合格率(以相对误差小于20%作为合格)，统计各模型最大相对误差(见上表)。相比之下，Copula预测方法预测精度更高更稳定。线性回归模型原理简单、计算便捷，但由于仅为线性拟合，不能深入分析变量间的相关关系，故应用有较大局限，这也是导致该模型在本实例分析中预测误差偏大的原因。而RBFNN模型具有运算速度快、能有效避免局部极小值出现等优点，但模型本身更适用于多影响因子的预测，故对单因子的情况而言尚有一定局限。

3 结 语

Copula函数将联合分布的构建分为确定边缘分布和分析相关性结构两部分，能够有力地捕捉变量间的非线性、非对称以及尾部相关关系，更加充分地利用已有信息，分析结果实用，是一种有效的构造联合分布函数、研究变量相关关系的方法。

基于Copula函数的Copula预测方法，利用Copula函数将变量的相关程度和相关模式有机结合，灵活适用地揭示变量之间复杂的协同变化特点，准确地捕捉变量联合分布尾部对称或非对称的相关关系，在此基础上研究因变量边缘分布与联合分布的关系，从而对因变量进行预测，因此具有较为精确的预测能力。Copula预测方法及其在年径流预测中的应用，为水文预测提供了一种全新的预测思路。fffffe

[1] 闫宝伟,郭生练,郭靖.基于Copula函数的设计洪水地区组成研究[J].水力发电学报,2010,29(6):60-65.

[2] 闫宝伟,郭生练,肖义.基于两变量联合分布的干旱特征分析[J].干旱区研究,2007,24(4):537-542.

[3] 陈士永,王祥三,张涛.Copula函数和AR模型在洪水随机模拟中的应用[J].水电能源科学,2009,27(2):1-7.

[4] 张晓伟,沈冰,黄领梅.基于BP神经网络的灰色自记忆径流预测模型[J].水力发电学报,2009,28(1):68-77.

[5] 张建兴,马孝义.生命旋回-Markov组合模型在年径流预报中的应用[J].水力发电学报,2008,27(6):32-36.

[6] 何小刚,杨大文.分布式水文模型与气象遥相关分析相结合的丹江口水库月入库径流预测[J].水力发电学报,2013,32(3):4-9.

[7] 魏艳华,张世英.Copula理论及其在金融分析上的应用[M].北京:清华大学出版社,2008.

[8] 王占海,陈元芳,黄琴.M-Copula函数在洪水遭遇中的应用研究[J].水电能源科学,2009,27(1):69-73.

[9] 詹道江,叶守泽.工程水文学[M].北京:中国水利水电出版社,2000.

[10] 王正发.MATLAB在P-Ⅲ型分布离均系数值计算及频率适线中的应用[J].西北水电,2007(4):1-4.

[11] 刘俊萍,畅明琦.径向基函数神经网络需水预测研究[J].水文,2007,27(5):12-15.

Prediction of Kaidu River annual runoff based on Copulas function

WEI Guanghui

(Xinjiang Tarim River Basin Administration, Korla 841000, China)

Accurate prediction of river runoff has important significance for reservoir scheduling and optimal allocation of regional water resources. In the paper, Kaidu River in Xinjiang is adopted as an example. Copulas function is utilized for organically combining relevance of the independent variable and dependent variable with related mode. Joint distribution function of two variables is constructed. Dependence structure between two variables and joint distribution is studied. On the basis, known independent variable probability distribution is combined for predicting unknown value of the dependent variable on the basis according to unknown dependent variable marginal distribution and joint distribution relationship of the sample value. The result shows that the prediction method based on copulas function has clear principle, simple calculation, stable performance and higher prediction accuracy.

annual runoff; prediction; Copulas functions; joint distribution; Kaidu River

10.16616/j.cnki.10-1326/TV.2016.07.019

TV123

A

2096- 0131(2016)07- 0066- 04