自增力液压楔形盘式制动器设计及效能仿真*

王军年 张垚 王庆年 李建华

（吉林大学 汽车仿真与控制国家重点实验室，长春 130025）

自增力液压楔形盘式制动器设计及效能仿真*

王军年 张垚 王庆年 李建华

（吉林大学 汽车仿真与控制国家重点实验室，长春 130025）

为提高制动器的制动效能、降低其促动功率消耗，改善整车燃油经济性，在传统的盘式制动器基础上，提出了一种新型液压促动楔形自增力盘式制动器。对其工作原理进行分析，并确定了关键设计参数和设计方法。通过AMESim仿真对比分析，论述了其关键设计参数对制动效能因数以及自锁现象的影响。得出了较为完善、合理的楔形盘式制动器设计方法。

主题词:楔形盘式制动器 自增力 制动效能因数 楔角 自锁

1 前言

盘式制动器与鼓式制动器相比具有更好的热稳定性，得到了广泛的应用，甚至商用车也开始使用气压盘式制动器[1～2]，然而由于其制动效能与鼓式制动器相比仍偏低，限制了其在重型商用车上的使用。

与在载货汽车上使用的楔形鼓式制动器工作原理不同[3]，楔形自增力盘式制动器是在原有盘式制动器上加入楔块形成的。在国内，相关文献比较少见[4]，国外开发的此种新型制动器的样品多数采用电机作为促动装置，并将其集成到电子机械制动器为核心的线控制动系统中[5]。2002年，Henry Hartmann等人提出了一种电动楔形制动器[6]，此后Semsey[7]、Fox[8]和Joo[9]等人先后提出了类似的电动楔形盘式制动器；2012年，Emam等人也提出了一种电控楔形制动器，并讨论了不同结构和控制参数对其制动效能的影响[10]；Dong Hwan Shin等人对楔形制动器的控制方法提出了新的尝试[11]；Kwangjin Han等人对于提高制动器的制动效能及自增力系数提出了相关控制策略[12]。但上述研究均以电机作为执行机构，使得其结构复杂、成本高，也增加了电制动器失效的可能性[13]；另一方面，上述文献多讨论楔角对制动效能的影响，而对于促动角及楔块摩擦因数对制动效能影响的研究较少。Junnian Wang等人提出了一种新型的液压楔形盘式制动器，并讨论了楔角对制动器自增力系数的影响[14]，但并未对促动力方向以及相关摩擦因数对自锁现象等制动器性能的影响进行讨论。

本文提出的液压促动楔形自增力盘式制动器（以下简称楔盘式制动器）基于传统液压盘式制动器进行了结构改进，对楔盘式制动器楔角大小的选择、制动块（楔块）受力方向（促动方向）的选择以及自锁现象进行了详细分析，并验证了楔盘式制动器的优势和设计方法的正确性。

2 楔盘式制动器基本原理

楔盘式制动器的基本结构如图1所示。在车辆正常行驶过程中，制动摩擦片与制动盘之间存在一定微小间隙，对车辆的行驶不产生影响。车辆需要制动时，活塞推动楔块沿滚针所在平面向制动盘方向运动，进而使制动摩擦片与制动盘表面相接触。合理的楔角与合适的促动力方向会使得楔盘式制动器有更好的制动效能因数，从而缩短制动时间并可达到一定的节能目的。制动过程结束时，在回位装置以及由于密封圈的变形而产生的回复力的共同作用下，楔块返回初始位置。

在这一过程中，一旦楔角的大小选取不当，就会使楔块退回初始位置所需的回复力过大，造成楔块无法顺利退出，从而无法结束制动过程，影响车辆的正常行驶。

图1 楔盘式制动器结构示意

3 制动器参数匹配设计

3.1 楔角大小与促动力方向

制动器在制动过程中的受力分析如图2所示。制动时，对楔块水平方向与垂直方向分别列受力平衡方程可得：

式中，F为作用在楔形块上的促动力；f=uN为楔形块与卡钳上滚针轴承接触面上产生的摩擦力；u为楔形块与滚针轴承接触表面的摩擦因数；N为滚针轴承对楔形块的压力；f1=u1N1为制动盘对制动摩擦片的摩擦力；u1为与楔形块相连的制动摩擦片表面与制动盘表面之间的摩擦因数；N1为制动盘对制动摩擦片的压力；α为楔块的楔角；β为促动力与水平方向的夹角。

式（1）整理可得：

由此可求得楔盘式制动器的制动效能因数为：

图2 制动过程受力分析

在制动器的设计过程中，通常将制动摩擦片表面与制动盘之间的摩擦因数控制在0.3～0.5范围内[15～16]，这里可以取u1=0.4，带有保持架的滚针轴承摩擦因数一般在0.002～0.003之间，这里可以取u=0.001 5。将u与u1的数值代入式（3）中，可以得到楔盘式制动器的Kef与α和β之间的函数关系，如图3所示。

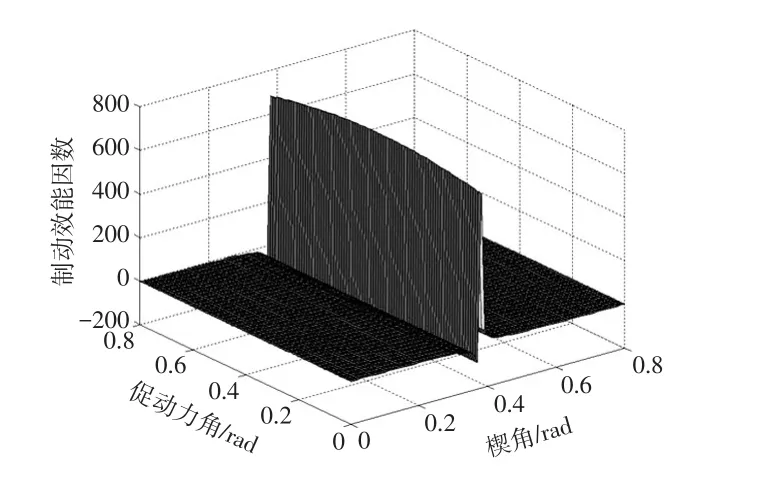
图3 Kef与α和β的关系

由图3可以看出，楔角接近0.4 rad时，制动效能因数有明显的变化，而楔角在其他数值时，制动效能因数则在0附近，这是关系式中（tanα-u1）这一项的变化引起的，因此在选择楔角时要保证其为正的同时数值较小，以保证获得较大的制动效能因数。通过图3还可以看出，在楔角相同的条件下，对应于不同的促动力方向，制动效能因数也有一定的变化。

为了更为清晰地比较，绘制了α取值分别为0.4 rad、0.5 rad和0.6 rad等3个较为关键的楔角时，促动力方向与制动效能因数之间的关系曲线，如图4所示。由图4可知，只有当β与α的大小相同时，Kef最大。故为得到更大的制动效能因数，可以将式（3）中的β替换为α，则有：

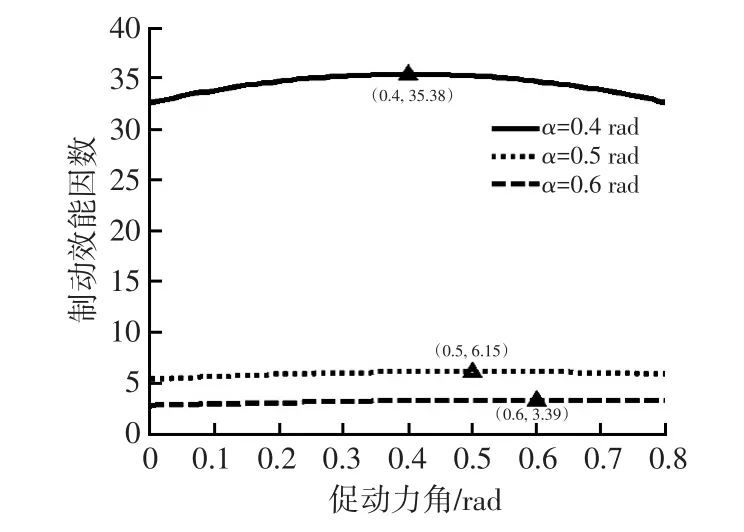
图4 不同楔角条件下β与Kef的关系

β与α大小相等时，重新绘制制动效能因数与楔角之间的关系曲线，如图5所示。楔角可根据图5所示的关系曲线选择，并应尽可能选取对应较大的制动效能因数的楔角。根据u与u1的取值范围以及图4、图5所示的制动器楔角与制动因数的理论关系，依据式（4）可得满足条件的α的范围0.379 rad＜α＜0.759 rad。

图5 α与Kef的关系

在选择楔角时，除了需要满足制动效能因数的要求，还要保证楔盘式制动器不出现自锁现象。制动过程结束、制动块退出时，楔盘式制动器的受力情况与图2所示制动时受力情况类似，此时楔形制动块促动力F变为回位力T，方向与促动力F相反，f的方向也随之相反。对楔形块水平方向以及垂直方向进行自由体受力分析可得：

由于促动力会影响制动摩擦片的以及摩擦力f1的大小，最终影响T的大小，最终求解出的T可用带有促动力F的表达式来表示：

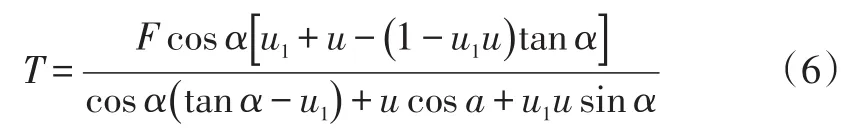
定义自锁系数C为楔形块退出时所需的拉力与制动时的促动力的比值，数值为正表明拉力方向与促动力方向相反，存在自锁趋势，数值为负表明拉力方向与促动力方向相同，不存在自锁趋势。将式（6）作简单整理可得自锁系数为：

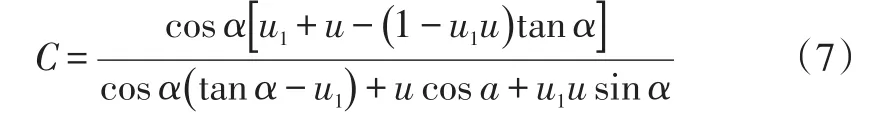
由于式（7）分母中存在（tanα-u1）项，根据式（7）绘制的楔角与自锁系数之间的关系曲线（见图6）中，在α=0.38 rad时发生由负到正的突变。此外，楔角在大部分的范围内，自锁系数均约为-1，不存在自锁趋势。

图6 α与C的关系

将u=0.001 5与u1=0.4分别带入式（7），求得满足C＞0的α的取值范围为0.379 rad＜α＜0.382 rad，说明只有楔角在此范围内，自锁现象才有可能发生，而这一范围也在考虑制动效能因数时楔角的最佳选择区间内。因此，在设计楔盘式制动器时，应综合考虑楔角对制动效能因数与自锁系数的影响，保证自锁系数在合理范围内的情况下，选取最佳的楔角使得制动效能因数最大。

根据以上原则，在同时考虑制动效能因数与自锁因素时可得在u=0.001 5与u1=0.4条件下的楔角选择范围为0.382 rad＜α＜0.759 rad。由图5可知，在这一范围内制动效能因数随楔角的增加而减小，因此0.382 rad为该条件下能够得到最大制动因数的楔角最佳值。

3.2 摩擦因数的匹配

在讨论楔盘式制动器的自锁问题时，除楔角α外，楔形块与滚针轴承接触表面的摩擦因数u对自锁的影响同样不能忽视。

在楔块与卡钳之间加入滚针轴承来减小接触面的摩擦因数，是因为在这一接触表面产生的摩擦力总是与施加在楔形块上的作用力的方向相反，这就意味着此处较大的摩擦因数会带来较大的需求促动力与回复力。一旦需求的回复力变大，就很有可能造成自锁现象，影响制动器的性能。

另一方面，即使楔形块与卡钳的摩擦因数很小，在某些楔角取值情况下也会对楔盘式制动器是否自锁产生影响。在u1选定为0.4的情况下，不同的α取值对u与C关系的影响如图7所示。由图7可以看出，对于不同的楔角取值，C出现极值的位置也会发生变化，同时，在u的常见取值范围内，α＞0.375 rad时，对自锁系数的影响明显变小。因此，在楔盘式制动器的设计过程中，滚针轴承的匹配需验证其楔块与滚针轴承接触表面的摩擦因数不会导致制动器产生自锁。

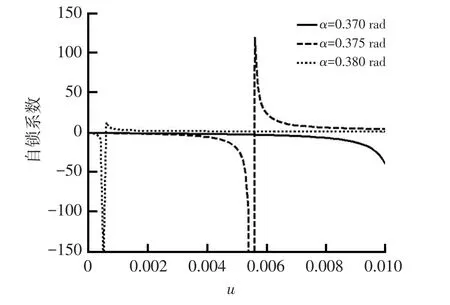
图7 不同楔角条件下u与C的关系

4 性能仿真对比验证

4.1 模型的建立

本文采用AMESim软件与Matlab软件联合仿真的方式，对楔盘式制动器的制动效能进行验证。其中，AMESim软件用于搭建整车模型，楔盘式制动器的模型搭建采用Matlab/Simulink完成。图8所示为楔盘式制动器模型。

图8 楔盘式制动器模型

4.2 制动效能对比

首先，以同一汽车分别装备传统制动器和楔盘式制动器，模拟从某一匀速行驶车速以相同制动减速度减速到相同车速时的促动力大小。此时楔盘式制动器楔角为0.5 rad，制动过程车速变化如图9所示，图10所示为传统制动器与楔盘式制动器在这一过程中的促动力对比。

图9 车速仿真曲线

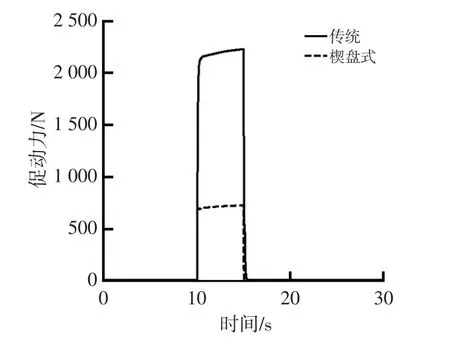
图10 促动力仿真曲线

从图10中可以看出，在几乎相同的制动减速度情况下，楔盘式制动器所需的促动力较传统制动器小。也就是说，在制动总功率相同，即制动效能相同时，楔盘式制动器具有更低的制动器促动力。由此可以判定，由于制动时间相同，楔盘式制动器更加省力、更加节能。同样，在保持促动力相同的情况下，楔盘式制动器可以带来更好的制动效果。

4.3 促动角对制动效能的影响

分别装备相同楔角但不同促动角的5种楔盘式制动器，模拟从某一匀速行驶车速以相同制动减速度减速到相同车速时的促动力大小，制动过程车速变化与图9所示一致。

图11所示为在相同楔角情况下（α=0.5 rad），不同促动角对应的楔盘式制动器促动力仿真曲线。从仿真结果可以看出，在制动减速度和制动时间相同的情况下，与β=0.5 rad相对应的楔盘式制动器所需的促动力最小。这与理论推导结论相一致，即促动力角大小与楔角大小相等时，制动效能因数最大。

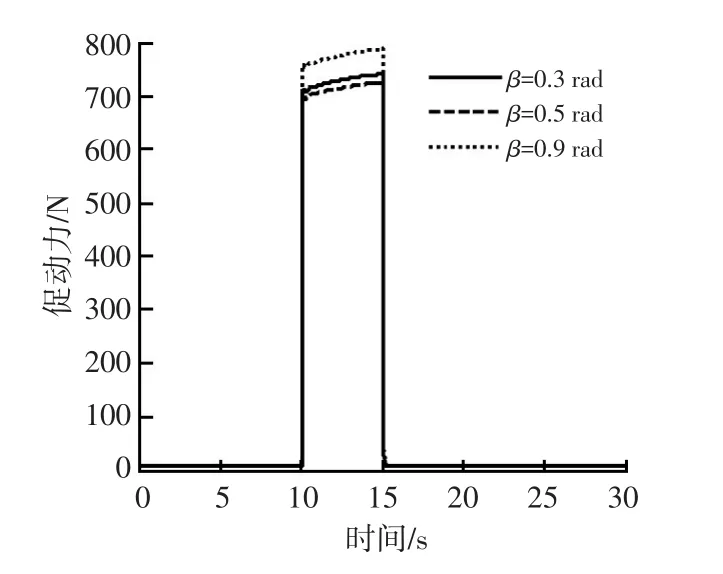
图11 促动力仿真曲线

4.4 楔角对制动效能的影响

分别装备不同楔角（促动角与选定的楔角实时相等）的5种楔盘式制动器，模拟从某一匀速行驶车速以相同制动减速度减速到相同车速时的促动力大小。这5种制动过程车速变化与图10所示一致。此时u1=0.4，u=0.001 5，根据理论分析推导出的楔角的选取范围0.382 rad＜α＜0.759 rad，自0.4 rad起等间隔选取楔角的大小进行仿真，不同楔角情况下楔盘式制动器的促动力仿真曲线如图12所示。从图12可以看出，制动过程所需的促动力随楔角增大而增大，与理论推导结果相符。此外，通过加入楔形块的方式，可以将促动力减小到约120 N，也说明了楔形盘式制动器能够明显改善制动性能的优势。

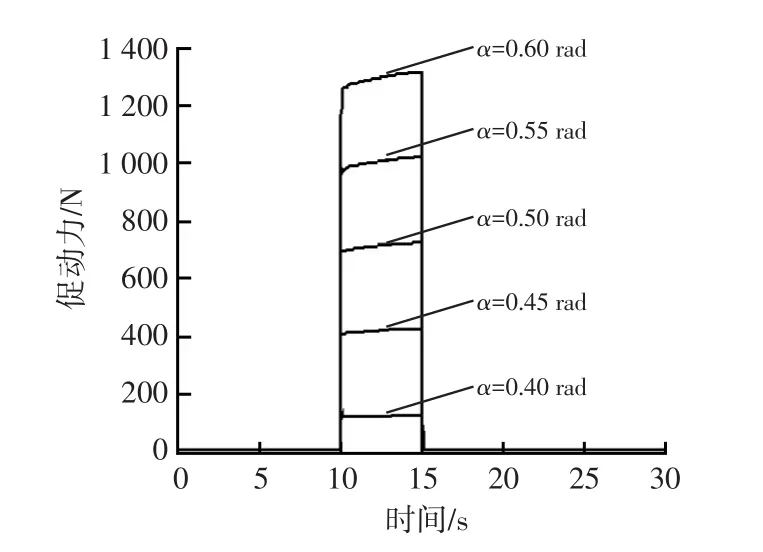
图12 促动力仿真曲线

5 结束语

本文利用楔形体静力学分析和联合仿真完成了自增力液压楔形盘式制动器的设计和效能对比分析，得到如下结论：

a.将制动器卡钳形状改变为楔形，可以明显改善制动器的制动效能；

b.选择促动角与楔角大小相等时制动器制动效能最好；

c.选择楔角大小时，不仅要考虑尽量增加制动效能因数，同时还应兼顾到出现自锁现象的可能性。

1 欧阳明高.新能源智能化电动汽车发展的角度谈“互联网+汽车+交通”.科学中国人，2015（25）：18～20.

2 严波，徐达.汽车气压盘式制动器的结构特点与性能分析.专用汽车.2005（4）：39～42.

3 许可芳.楔形制动器的开发与应用.汽车研究与开发.1995（1）：10～14.

4 王军年，杨南南，初亮，等.楔形自增力盘式制动器.中国发明专利，2012100430867.2013.

5 Dietrich J,Gombert B,Grebenstein M.Electromechanical brake with self-energization.US patent，6318513.2001.

6 Hartmann H,Schautt M,Pascucci A,et al.eBrake®the mechatronic wedge brake.SAE Paper No.2002-01-2582，2002.

7 Semsey À,Roberts R.Simulation in the development of the electronic wedge brake.SAE Paper No.2006-01-0298，2006.

8 Fox J,Roberts R,Baier-Welt C,et al.Modeling and control of a single motor electronic wedge brake.SAE Paper No.2007-01-0866，2007.

9 Kim J G,Kim M J,Kim J K.Developing of electronic wedge brake with cross wedge.SAE Paper No.2009-09-0856，2009.

10 Emam M A A,Emam A S,El-Demerdash S M,et al.Performance of automotive self reinforcement brake system.Journal of Mechanical Engineering，2012（1）：4～10.

11 Shin D H,An J N.Study of stiffness design of caliper for reducing the weight of an electro wedge brake.Applied Mechanics and Materials，2012，138/139：159～162.

12 Han K,Kim M,Hnh K,et al.Modeling and control of an electronic wedge brake.Proceedings of The Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science，2012，226（7）：1693～1704.

13 王玉群，林向阳，杨清林.汽车电子机械制动器（EMB）的发展研究.轻型汽车技术.2009（9）：20～23.

14 Wang J,Yang N,Wang Z,et al.Design and Simulation of a Novel Wedge Disc Brake.FISITA 2012 World Automotive Congress，Beijing，2012.

15 赵凯辉，魏朗.制动器摩擦副摩擦因数研究.汽车技术.2009（3）：25～28.

16 施瑞康，张德林.汽车制动器制动效能因数计算及结果分析.汽车技术.2005（6）：1～5.

（责任编辑 斛 畔）

修改稿收到日期为2016年9月19日。

Design and Braking Efficiency Simulation for Self-Reinforcement Hydraulic Wedge Disc Brake

Wang Junnian,Zhang Yao,Wang Qingnian,Li Jianhua
（State Key Laboratory of Automobile Simulation and Control,Jilin University,Changchun 130025）

In order to increase braking efficiency,reduce actuating power consumption,and improve vehicle fuel economy,a novel self-reinforcement wedge disc brake actuated by hydraulic power was proposed,based on the traditional disc brake.Firstly,the working principle was analyzed to define the critical design parameters and design methods.Then through analysis and comparison in AMESim simulation,the influence of the relevant key parameters on the braking efficiency factor and self-locking was discussed in detail.Finally,a complete and rational design method of the novel wedge disc brake was derived.

Wedge disc brake,Self-reinforcement,Braking efficiency factor,Self-locking

U463.51+2

A

1000-3703（2016）11-0001-05

国家自然科学基金项目（51205153）；吉林省自然科学基金项目（20140101072JC）。