如何用向量方法判断几何图形的形状

宋 玉●

南京艺术学院附属中等艺术学校(210013)



如何用向量方法判断几何图形的形状

宋 玉●

南京艺术学院附属中等艺术学校(210013)

用向量研究几何图形的形状体现了平面向量的代数与几何的双重属性，它体现了向量形式的多样性和向量运算的灵活性，它体现了高考很重要的一个数学思想方法：数形结合.

特殊形状；数量积公式；坐标形式；共线定理.

平面向量这一章中有一个典型的例题，就是利用向量的方法判断几何图形的形状.笔者认真地翻看了一下教材，发现这类题目有十几个之多.笔者把这些例题作了修改整理，并让学生们练了一下.练下来的结果并不太理想.其中最典型的错误，就是判断不全面.于是笔者与学生一起认真地研究了这一类型题目的解题方法，有了一些心得体会.

首先要清楚三角形、四边形有哪些特殊形状，它们的特点分别是什么.三角形主要分为：等腰三角形(两条边相等或两个内角相等)；直角三角形(一个内角为 )；等边三角形(三条边相等或三个内角相等).四边形主要分为：平行四边形：矩形(邻边垂直或对角线相等)；菱形(邻边相等或对角线垂直)；正方形(综合矩形和菱形的特点).梯形：等腰梯形(一组对边平行，另一组对边不平行且相等);直角梯形(一个内角为90°) .

其次要清楚用向量判断形状的主要方法有哪些.

常用的方法主要有向量的数量积、向量的坐标公式、向量的共线定理、向量的运算法则作图等方法.比如说判断两条边垂直，常用到a·b=0或x1x2+y1y2=0这两个公式；判断一组对边平行且相等，则需得a=b就可以；判断两个向量平行，常用到b=λa或x1y2-x2y1=0这两个公式.

以上两点弄清楚以后，在具体做题时还会遇到各种各样的问题，因此还需要多做一些相关例题，达到融会贯通，熟能生巧的效果.下面笔者举例说明.

一、用向量数量积公式判断形状

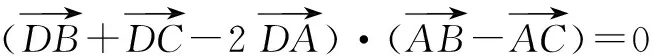
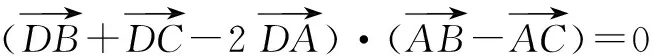
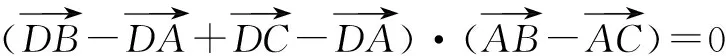
二、用向量坐标公式判断形状

例2 已知△ABC的三个顶点坐标为A(-1,8)，B(-4,1)，C(1,3)，则△ABC的形状为____.

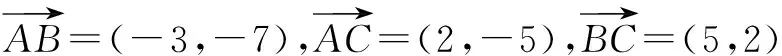
错因分析 有的学生判断结果是直角三角形,这个答案并不准确.笔者与学生交流之后，发现有的学生是先画简图，凭感觉看出有直角.而有的学生用坐标法判断出直角后，就没再深究下去，因而判断不准确.我们师生针对这个问题研究出了判断三角形形状的一般方法.

步骤一：算出三个向量坐标，先找垂直关系；

步骤二：如果有垂直关系，比如AC⊥BC，则先确定是直角三角形，再继续判断这两个向量模是否相等；如果没有垂直关系，则继续判断三个向量的模是否相等.看是否是等腰或等边三角形.即先判断位置关系再判断数量关系.

例3 已知四边形ABC的四个顶点坐标为A(5,1),B(3,5),C(7,3),D(9,-1)，则四边形ABCD的形状为____.

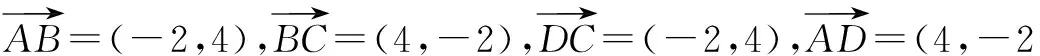
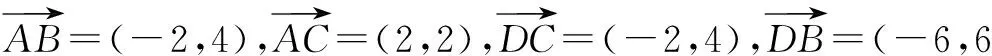
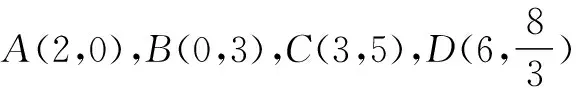
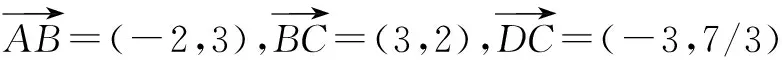
步骤二 如果是平行四边形，则继续判断邻边的关系，若邻边满足相等关系，则是菱形；若满足垂直关系，则是矩形；如果都满足则是正方形(也可以从对角线角度分析，但如果是梯形，则判断邻边是否垂直，两个腰是否相等).

阶段总结 教材中大多是给出四边形的形状，求某一个点的坐标，有时可能会出现两解的情况.笔者将其改为由四点判断形状，主要目的不是为了加深难度，而是希望达到让学生熟练利用向量的坐标公式来解决问题的目的.

G632

B

1008-0333(2016)28-0043-01