安全完整性等级验证计算在化工装置中的应用研究

张兆祥，李涛

(华陆工程科技有限责任公司，西安 710065)



安全完整性等级验证计算在化工装置中的应用研究

张兆祥，李涛

(华陆工程科技有限责任公司，西安 710065)

安全完整性等级(SIL)验证计算是安全仪表系统设计中重要的组成部分。介绍了SIL及验证计算方法，结合工程实例对典型的安全回路进行SIL验证计算，将计算结果和安全评估的SIL进行比较，确定回路安全仪表功能满足相应的SIL要求；通过对比IEC 61508-6与ISA-TR84.00.02-2两个标准的计算结果以及不同检测周期对两个标准计算结果的影响，阐述了两个标准的计算特点以及检测周期的选择对验证计算的意义。

安全完整性等级 平均失效概率 验证计算 检测周期 安全仪表系统

安全完整性等级SIL(safety integrity level)是用来表示安全仪表系统安全完整性要求的离散等级，通过平均失效概率(PFDAVG)量化进行分级，平均失效概率越低，SIL越高，见表1所列。根据IEC 61508[1-2]及IEC 61511[3-4]的规定，通过定性或定量分析方法进行评估和确定，常用的方法包括危害与可操作性分析(HAZOP)、过程安全保护层分析(LOPA)、风险矩阵法等。但在确定SIL后，对回路安全仪表功能是否满足SIL要求而进行的验证计算涉及较少，笔者从SIL验证的过程出发，结合实例分析，进行SIL验证计算，以期为SIL验证计算提供借鉴。

1 SIL验证

按照文献[1]及文献[3]的要求，在安全仪表系统的安全生命周期内，即从项目设计阶段开始到所有的安全仪表功能不再适用为止，都应确保安全仪表系统能满足SIL要求。安全仪表系统在设计安装完成后需要对其进行功能安全评估，以明确其安全功能所达到的SIL，即使在装置运行多年后，进行技术改造时也应对装置的SIL进行功能安全评估，如不能达到确定的SIL，则应对安全仪表系统进行改造，所以对于新建和改造项目SIL的验证计算非常重要。

1.1 安全完整性等级

SIL反映了安全仪表系统执行安全功能时，在规定的时间内、在所有规定的条件下满足执行要求的安全仪表功能的平均概率，SIL级别越高，正确执行所要求的安全仪表功能的概率也越高。IEC 61511将安全仪表功能的操作模式分为“低要求操作模式”和“连续操作模式”(或“高要求操作模式”)。

1) “低要求操作模式”是指响应过程条件或其他要求而采取一个规定动作(如关闭阀门)，在“低要求操作模式”时，安全仪表功能的SIL用PFDAVG衡量，见表1所列，通常化工装置的安全仪表系统工作于“低要求操作模式”，本文后续的论述均按“低要求操作模式”进行验证计算。

表1 “低要求操作模式”时平均失效概率

2) “连续操作模式”是指在安全仪表功能的危险失效时间中，如果不采取预防动作，即使没有进一步的失效，潜在危险也会发生。在“连续操作模式”时，安全仪表功能的SIL用每小时危险失效频率衡量。

1.2 SIL验证计算方法

SIL验证计算的主流方法有可靠性框图、故障树分析和马尔可夫模型三种[5]。

1.2.1 可靠性框图

可靠性框图表示系统内部元件的传递过程，可以直观地表示元件的逻辑关系，如图1所示。

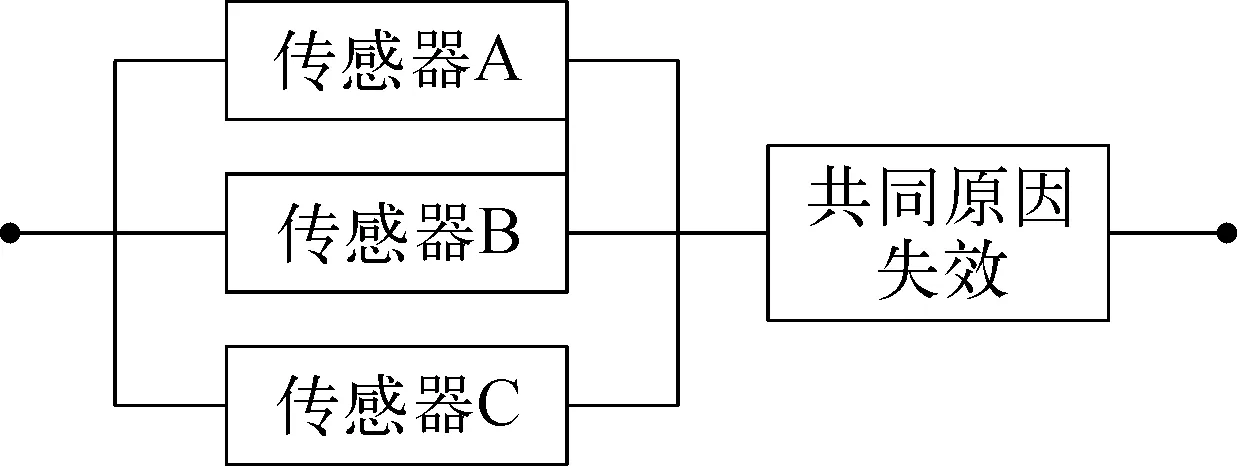
图1 传感器“2oo3”表决结构的可靠性框图示意

可靠性框图是IEC 61508-6和ISA-TR 84.00.02-2都推荐采用的SIL验证计算方法，区别在于计算公式不同，笔者拟采用可靠性框图进行实例分析。

1) IEC 61508-6附录中定义的安全仪表系统平均失效概率及4种表决结构的平均失效概率的计算公式分别介绍如下：

a) 安全仪表系统平均失效概率的计算公式：

PFDSYS=PFDS+PFDL+PFDFE

(1)

式中：PFDSYS——安全仪表系统要求的平均失效概率；PFDS——传感器子系统要求的平均失效概率；PFDL——逻辑子系统要求的平均失效概率；PFDFE——最终元件子系统要求的平均失效概率。

b) “1oo1”的计算公式：

PFDAVG=(λDU+λDD)

(2)

式中：T1——验证测试周期，h；MTTR——平均修复时间，h；λD——子系统中通道的危险失效率；λDU——未检测到危险失效率；λDD——检测到的危险失效率。

c) “1oo2”的计算公式：

(3)

式中：β——公共故障系数；βD——已检测到的失效百分比；tCE——表决结构中通道的等效平均停止工作时间，h；tGE——表决结构中表决组的等效平均停止工作时间，h。

d) “2oo2”的计算公式：

PFDAVG=2λDtCE

(4)

e) “2oo3”的计算公式：

PFDAVG=6((1-βD)λDD+(1-β)λDU)2tCEtGE+

(5)

2) ISA-TR 84.00.02-2定义的安全仪表系统平均失效概率及4种表决结构的平均失效概率的简化计算公式介绍如下[6]：

a) 安全仪表系统平均失效概率的计算公式：

PFDSIS=∑PFDSi+∑PFDAi+

∑PFDLi+∑PFDPSi

(6)

式中：PFDA——安全回路最终元件的平均失效概率；PFDPS——安全回路电源的平均失效概率；i——安全回路中组成元件的数量。

如安全仪表系统设计为故障失电，系统故障后处于安全状态，则电源的平均失效概率PFDAVG不影响SIL验证计算，此时式(6)等同于式(1)。实际验证计算中，通常不涉及共同原因失效以及系统性失效，如果修复时间较短，可以忽略在修复期间存在的多重失效。

b) “1oo1”的计算公式：

(7)

c) “1oo2”的计算公式如下：

(8)

d) “2oo2”的计算公式：

PFDAVG=λDUT1

(9)

e) “2oo3”的计算公式：

(10)

通过对比，可以看出ISA-TR 84.00.02-2定义的计算公式更为简洁、方便。

1.2.2 故障树分析

故障树分析是ISA-TR 84.00.02-3推荐采用的SIL验证计算方法，通过对顶部事件进行追根溯源的层次分析从而得到系统的失效概率，模型易于理解，可对复杂系统进行分解，生成的部分可以进行进一步故障树分析。

1.2.3 马尔可夫模型

马尔可夫模型是ISA-TR 84.00.02-4推荐采用的SIL验证计算方法，定义系统中全部互斥的成功/失效状态，系统在某个时间点只能处于某一个状态，系统由一种状态以某种概率转移到另一种状态，此状态的下一步转移完全独立，状态用带编号的圆圈来表示，状态之间的转换用箭头转移弧来表示，并标注相应的失效率和维修率，用来描述系统随时间变化的行为。然而，构造大型的马尔可夫模型非常费时、费力，求解也非常困难，不如可靠性框图直观，在验证计算过程中使用较少。

1.3 SIL验证计算流程

安全完整性等级验证计算流程如图2所示，安全仪表系统中相关元件包括变送器、逻辑控制器、继电器、电磁阀等都需取得TÜV Rheinland认证、Exida认证或其他安全认证机构的认证，并在认证

证书上标明计算安全完整性等级所需要的参数。

图2 安全完整性等级验证计算流程示意

2 实例分析

某炼化二期项目丁辛醇装置采用英国DAVY的工艺包，经HAZOP分析审查后，确定了安全仪表回路需要达到的安全完整性等级。文中以该装置中典型安全回路为例进行验证计算，通过采用IEC 61508-6和ISA-TR 84.00.02-2分别计算安全回路各子系统(传感器/逻辑解算器/最终元件)及整个回路的平均失效概率，验证安全仪表回路的安全完整性等级能否满足要求，并对计算结果进行分析。

2.1 罐区储罐安全回路

液位是储罐的1个重要的工艺参数，如液位过高，储罐内压力上升，可能带液至低压火炬总管，造成比较严重的后果，经HAZOP分析后将液位安全回路定义为SIL1；安全仪表系统设置1台雷达液位计(LAHH-50105)检测液位，液位过高时紧急切断给料阀(XV-50103)，输入回路和输出回路均为“1oo1”表决结构，如图3所示。经查询各元件安全认证证书，相关安全参数见表2所列。

图3 储罐安全仪表回路示意

表2 平均失效概率计算(储罐安全回路)

表2内输入元件(LAHH-50105)的PFDAVG1，PFDAVG2分别采用“1oo1”式(7)，式(2)计算得出；逻辑控制器及输出元件(XV-50103)的PFDAVG1，PFDAVG2为厂商提供；再分别经式(6)，式(1)计算，可得出储罐安全回路失效概率PFDSIS分别为3.776×10-3和3.872×10-3，对比表1，完全满足SIL1的要求。

2.2 粗辛醇收集槽安全回路

粗辛醇收集槽液位过高，可能带液至K-301氢气压缩机，对氢气压缩机的安全运行造成极为不利的影响，损失较大，经HAZOP分析后将液位安全回路定义为SIL1，安全仪表系统设置3台双法兰差压变送器(LAHH-30602/30603/30605)检测液位，液

位过高时切断去粗辛醇收集槽的循环管线流量调节阀(FZSOV-30803)，输入回路为“2oo3”表决结构，输出回路均为“1oo1”表决结构，如图4所示。经查询各元件安全认证证书，相关安全参数见表3所列。

图4 粗辛醇收集槽安全仪表回路示意

表3 平均失效概率计算(粗辛醇收集槽安全回路)

表3内输入元件(LAHH-30602/30603/30605)的平均失效概率PFDAVG1，PFDAVG2分别采用“2oo3”并由式(10)，式(5)计算得出；输出元件(FZSOV-30803)的平均失效概率PFDAVG1，PFDAVG2分别采用“1oo1”并由式(7)，式(2)计算；再分别经式(6)，式(1)计算，得出粗辛醇收集槽安全回路失效概率PFDSIS分别为9.21×10-4和9.367×10-4，对比表1，也完全满足SIL1的要求。

2.3 计算结果分析

笔者分别采用IEC 61508-6和ISA-TR 84.00.02-2公式计算安全回路的平均失效概率，计算结果偏差不大，对于“1oo1”表决结构，子系统平均失效概率计算结果基本吻合；对于“2oo3”表决结构，输入元件平均失效概率计算结果相差较大，按照ISA-TR 84.00.02-2计算的平均失效概率更低。

文中选取“1oo1”，“2oo3”两个典型的表决结构进行实例分析，通过公式及计算结果不难发现“2oo3”表决结构比“1oo1”的平均失效概率更低，通

过“2oo3”表决结构可以大幅度地降低各子系统的平均失效概率，从而使安全回路的安全完整性等级得以提高，特别是对于回路安全完整性等级要求很高(如SIL3)，而单台仪表无法到达SIL3的要求，可以通过“1oo2”，“1oo3”，“2oo3”等表决结构来实现。

从以上公式中不难看出，确定检测周期T1事关重大，它直接影响平均失效概率的计算，同时需要兼顾多方面的因素，检测周期越长，对仪表的要求越高；检测周期越短，对工艺过程带来的风险越大。笔者将检测周期调整为3a进行对比，计算结果见表4，表5所列，储罐安全回路平均失效概率PFDSIS，PFDSYS分别为1.217×10-2和1.219×10-2，粗辛醇收集槽安全回路平均失效概率PFDSIS，PFDSYS分别为3.349×10-3和3.391×10-3。对比发现，安全回路的计算平均失效概率相差较大，在安全完整性等级评估要求较低时易满足要求，若完整性等级评估要求较高(如SIL3)，则检测周期影响较大，因而检测周期的确定应引起足够的重视。

表4 检测周期调整为3a的平均失效概率(储罐液位安全回路)

表5 检测周期调整为3a的平均失效概率(粗辛醇收集槽安全回路)

3 结束语

通过安全完整性等级验证计算，确保了安全仪表系统的安全完整性，根据验算结果合理地配置安全仪表系统，有效地防止和降低各类风险的发生，使安全仪表系统的设计和执行达到最优化，对于装置的长期平稳安全运行意义重大。由于手工进行SIL验证计算效率低下，且易出现误差，特别是对于复杂的安全回路，因而采用专门的SIL计算软件是比较可行的方法。目前SIL验证计算软件主要有Exida公司的exSILentia软件；加拿大ACM自动化有限公司的SilCore软件，HIMA的SILence软件等[9]，可减轻验证计算的工作量，便于在设计过程中进行验证调整。

[1] IEC. IEC 61508—2010：Functional Safety of Electrical， Electronic， Programmable Electronic Safety-related Systems [S]. Geneva：IEC，2010.

[2] 中国机械工业联合会. GB/T 20438—2006 电气、电子、可编程电子安全相关系统的功能安全[S].北京：中国标准出版社，2006.

[3] IEC. IEC 61511—2003：Functional Safety：Safety Instrumented Systems for the Process Industry Sector [S]. Geneva：IEC， 2003.

[4] 中国机械工业联合会.GB/T 21109—2007过程工业领域安全仪表系统的功能安全[S].北京：中国标准出版社，2007.

[5] 赵亮.80万吨/年甲醇项目安全完整性等级(SIL)回路计算实例分析[J].自动化博览，2011(03)：64-67.

[6] ISA. ISA-TR 84.00.02—2002 Safety Instrumented Functions (SIF)-Safety Integrity Level (SIL) Evaluation Techniques [S]. North Carolina：ISA， 2002.

[7] 王伟.安全仪表系统的安全性与可用性研究[J].自动化与仪表，2015(06)：73-76.

[8] 严春明.SIL评估技术在甲醇装置中的应用[J].石油化工自动化，2014，50(03)：5-8.

[9] 吴宁宁.安全仪表系统的Markov建模方法研究[J].计算机与应用化学，2009，26(06)：821-824.

[10] 庄力健，朱建新，方向荣，等.典型石化装置加热炉联锁系统安全完整性评估与现状[J].化工自动化及仪表，2015，42(01)：31-35.

[11] 黄会伟，袁印实，史玉颖.风险图表法安全完整性等级评价方法[J].化工自动化及仪表，2014，41(02)：115-119.

[12] 朱春丽，洪毅，丁伟晖.海洋石油平台安全仪表系统安全完整性等级评估[J].化工自动化及仪表，2014，41(04)：410-413.

Application Research of Safety Integrity Level Verification Calculation in Chemical Plant

Zhang Zhaoxiang, Li Tao

(Hualu Engineering & Technology Co. Ltd., Xi’an, 710065, China)

s：Safety integrity level (SIL) verification calculation is an important part in safety instrumented system design. SIL and its calculation methods are introduced. SIL verification calculation for typical safety loop is carried out with actual engineering case. Calculation result is compared with the result of safety evaluation SIL . Corresponding required SIL can be met with loop safety instrument function. By comparing calculation result of IEC 61508-6 and ISA-TR84.00.02-2, as well as influence to calculation result in different proof test intervals, characteristics of above two standards and significance of verified calculation in proof est interval selection are expounded.

safety integrity level; average probability of failure; verification calculation; proof test interval; safety instrumented system

张兆祥(1982—)，男，2008年毕业于华北电力大学控制理论与控制工程专业，现就职于华陆工程科技有限责任公司电控室，从事化工自控专业工程设计工作，任工程师。

TP202

B

1007-7324(2016)05-0028-05

稿件收到日期：2016-06-25，修改稿收到日期：2016-07-15。