基于不同参数模型的项目参数估计结果的比较

邹丽华

(大连教育学院 学习质量监测中心， 辽宁 大连 116021)



基于不同参数模型的项目参数估计结果的比较

邹丽华①

(大连教育学院 学习质量监测中心， 辽宁 大连 116021)

参数估计是项目反应理论应用和发展的前提。本研究采用项目反应理论，使用PARSCALE4.1 软件，选择两参数和三参数罗杰斯蒂(Logistic)混合模型对某年区域初中毕业生中考物理测验成绩进行项目参数估计，发现不同参数的项目参数估计结果在不同程度上存在差异。

项目参数估计；能力参数估计；罗杰斯蒂模型

教育测量是评价教育结果的重要方法，教育测量不仅包括对考试结果的评价分析，也包括对试题试卷质量的评价分析。近年来，国内开始采用经典测量理论和项目反应理论联合使用，对测量数据进行精细分析。与经典测量理论相比，项目反应理论的优势在于，它可以计算出项目参数(试题难度、区分度)，还可以预估出考生能力参数；并且项目参数和能力参数彼此相互独立，即考生能力参数的估计不受所选用试题的影响，试题难度和区分度的估计也不受考生样本的影响，但项目参数的估值往往受到不同参数选择个数的影响。研究人员以某年初中毕业生中考物理学科成绩为例，分别用二参数罗杰斯蒂(Logistic)混合模型和三参数罗杰斯蒂(Logistic)混合模型对项目参数和考生能力参数进行参数估计，进而比较两种参数估计对项目难度和区分度结果的影响。

大连市初中毕业生学业考试物理试卷承担着毕业与选拔两种功能。本研究选择某一年大连市市内五区考生中考物理考试成绩，该试卷包括选择题、填空题、计算题、简答题和综合题五种题型，共31道题目，试卷满分值为90分。根据经典测验理论分析，测验Alpha信度系数0.920，物理试卷信度达到非常理想的程度。

一、项目反应理论常用的罗杰斯蒂模型

建立在潜在特质理论基础上的项目反应理论，通过建立考生作答反应与题目特征量及能力水平间关系的非线性模型，估计被试的能力水平和题目参数，同时也定义了信息函数。从数学角度看，项目反应理论用含有未知参数的数学模型表示被试答对项目的可能性，是建立在概率的基础之上。通常把试题难度、区分度、猜测系数称为项目参数，把被试的潜在特质称为能力参数。常见的模型有多级计分模型、等级模型、称名模型，通常采用的是二值计分的单参数、二参数和三参数Logistic模型。现以二值计分的三参数Logistic模型来说明项目反应理论。

项目反应理论三参数的模型(3PLM)为：

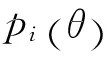
题目参数估计结果，项目难度估值一般在-3至+3之间；项目区分度一般大于零，原则上估值越大越好；项目猜测度越小，项目质量越好。根据项目参数估计的结果，就可以在此基础上分析项目质量及对题目进行筛选。项目难度是项目筛选的参考指标，但是难度值的高低并不是单个项目取舍的依据。分析者应考虑作为所选测验项目整体构成的难度分布与测验所要求的难度分布是否拟合，并以此作为取舍的原则。项目区分度和猜测度是单个项目取舍的依据，项目区分度一般不小于0.50，否则就应考虑删除，项目猜测度最大一般不应超过0.25。[1]

二、不同参数模型项目参数拟合结果的比较

研究中采用项目分析软件PARSCALE4.1对不同考生的能力值和项目参数值进行估计，选用的是二参数混合模型(二参数Logistic模型和分步评分模型)和三参数混合模型(三参数Logistic模型和分步评分模型)。用边际极大似然法估计项目的难度、区分度和猜测度；对能力估计时采用牛顿极大似然估计法(MLE)估计和后验期望估计(EAP)。

用PARSCALE4.1软件和选取Logistic混合模型对项目参数进行估计时，-2loglikelihood值是拟合统计量，表示模型和数据的拟合程度。这是一个相对统计量，用于模型比较，值越小拟合越好。最终二参数拟合统计量为698930.776，三参数为720646.935，显然是二参数模型与数据拟合的结果要比三参数的好。

1．单选题

中考物理选择题分为单项选择题和多项选择题，猜测度的估计是针对单选题而言的。物理单选题的特点是在题目中给出四个选项，其中只有一个正确选项。分别用二参数和三参数模型对单选题进行项目参数估值，结果见表1所示。

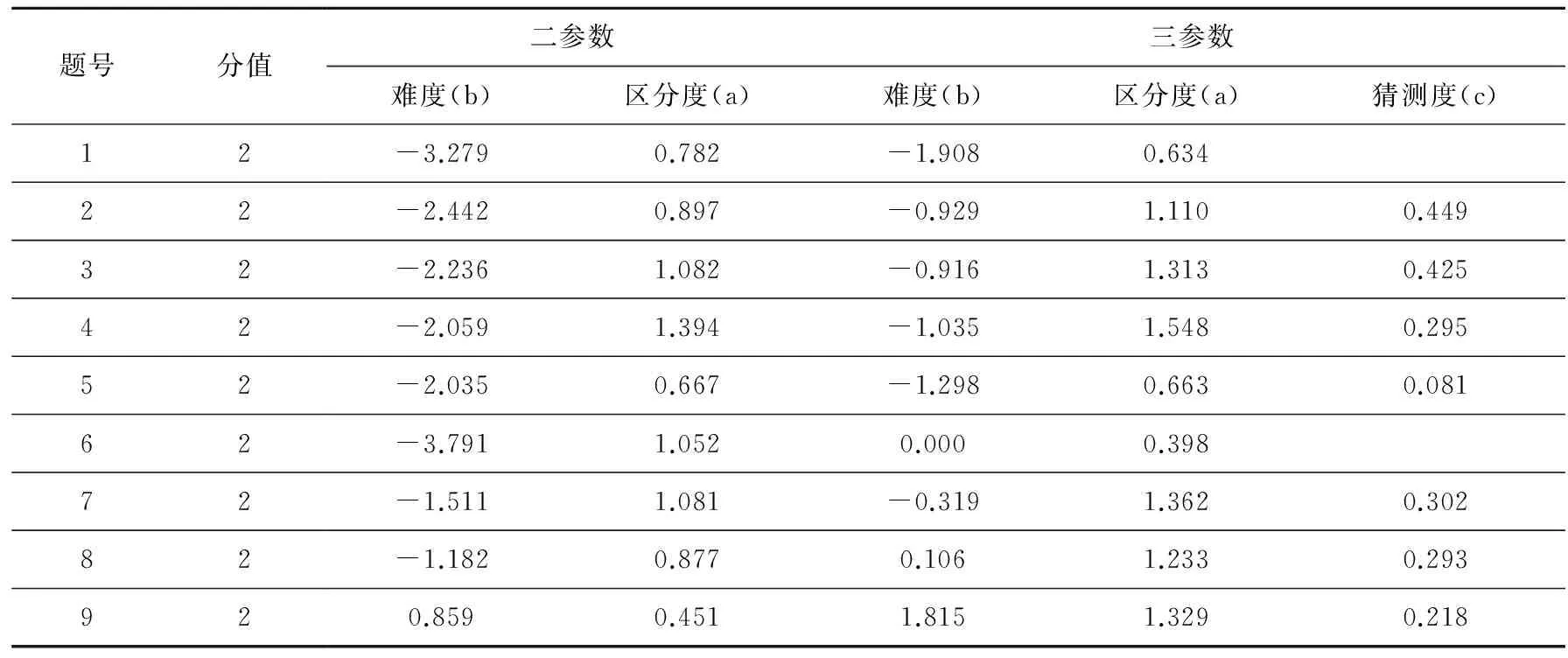
表1 单选题二参数混合模型与三参数混合模型项目参数估值的结果

由表1可知，同一道题不同参数模型估计的难度、区分度均有差异。同一道试题二参数的难度估值小于三参数的难度估值，项目难度估值相差较大。例如，第3题二参数的难度估值是-2.236，三参数的难度估值为-0.916。除了第1题和第6题，其他试题区分度估值，二参数的均小于三参数的。再例如，第8题二参数区分度估值为0.877，三参数区分度估值为1.233。说明猜测度的估计对题目难度和区分度参数估计有较大影响。从猜测度估值角度看，c值小于0.25有两个题目(第5、9题)，c值为0的有两道题(第1、6题)，c值大于0.25的有五道试题(第2、3、4、7、8题)。试题猜测度小，说明考生在该试题上不容易猜对。

2．多项选择题及主观题

多项选择题的特点是在题目给定的四个选项中选择正确的选项，正确选项可能不止一个。如果考生选择了错误选项，不给分；如果只选择了部分正确选项，就给试题满分的一半分；如果全选对了，就给满分。对多项选择题、主观题分别用二参数混合模型与三参数混合模型进行项目参数估计，结果见表2所示。

表2 多选题、主观题在二参数混合模型与三参数混合模型项目参数估值的结果

由表2可知，同一道题不同参数混合模型计算的难度估值有差异，二参数的难度估值小于三参数的难度估值，项目难度估值相差约为0.70，而试题区分度估值几乎没有差异，二参数与三参数相差不大于0.126。例如，第23题二参数的难度估值是-0.968，三参数的难度估值为-0.307；二参数区分度估值为0.502，三参数区分度估值为0.491。这说明对试题猜测度参数的估计，对试题难度估值有均衡影响，而对试题区分度几乎没有影响。由表2还可知，第10、11、12、31题的区分度在二参数和三参数混合模型的估值中均小于0.50，表明该试题对考生能力的区分功能不强。

三、思考与建议

1.中考物理项目参数拟合应选择二参数混合模型。从二参数模型与三参数模型的相关统计结果看，二参数与三参数难度值(b)的点二列相关系数为0.8662，区分度的点二列相关系数为0.7396。相对统计量的相关程度不高。建议在试题全部是客观题时，选择三参数的罗杰斯特混合模型为佳，否则要选择二参数混合模型为好,以保证估计结果的准确性。

2.中考物理命题应以考查能力立意为主，更好地体现中考的选拔功能。从考生能力预估与原始得分的结果看，将原始得分与2PL模型能力参数估值进行相关分析，相关系数为0.9693，相关程度比较高，表明考生物理得分能很好地代表学生的物理学业能力。中考学科测试虽然是兼顾水平和选拔两种测试功能，但中考物理考试基本上属于能力测试，死记硬背不得分。

[1] 戴海琦.基于项目反应理论的测验编制方法研究[J].考试研究，2006(4)：31-44.

[责任编辑：知然]

On Comparison of Estimates of Project Parameters from Different Parameter Models

ZOU Li-hua

(StudyQualityMonitoringCenter,DalianEducationUniversity,Dalian, 116021,China)

Parameter estimate is the premise of the application and development of project reaction theory. The study adopts project reaction theory, uses the software of PARSCALE 4.1, chooses two-parameter and three-parameter Logistic mixed model to estimate project parameters in terms of junior middle school graduates’ physics test results of one region, finding that differences of various degrees exist as far as parameter estimate results of different parameter projects are concerned.

project parameter estimate; ability parameter estimate; Logistic model

2016-06-22

辽宁省“十三五”教育科学规划课题“区域初中毕业生物理成就差异的实证研究”(JG16CB324)

邹丽华(1963- )，女，吉林吉林人，教授。

G632.479

A

1008-388X(2016)03-0075-03